Unity中Shader旋转矩阵(二维旋转矩阵)
文章目录
- 前言
- 一、旋转矩阵的原理
- 1、我们以原点为中心,旋转坐标轴θ度
- 2、求 P~2x~:
- 3、求P~2y~:
- 4、最后得到 P~2~点 的点阵
- 5、该点阵可以拆分为以下两个矩阵相乘的结果
- 二、在Shader中,使用该旋转矩阵实现围绕 z 轴旋转
- 1、在属性面板定义 float 变量作为旋转的角度θ
- 2、在常量缓冲区申明该变量
- 3、在 顶点着色器 定义旋转矩阵
- 4、用旋转矩阵乘以顶点的 xy 实现围绕z轴旋转
- 5、效果
- `围绕x轴旋转 和 围绕y轴旋转,我们可以修改 .xy 来实现。` 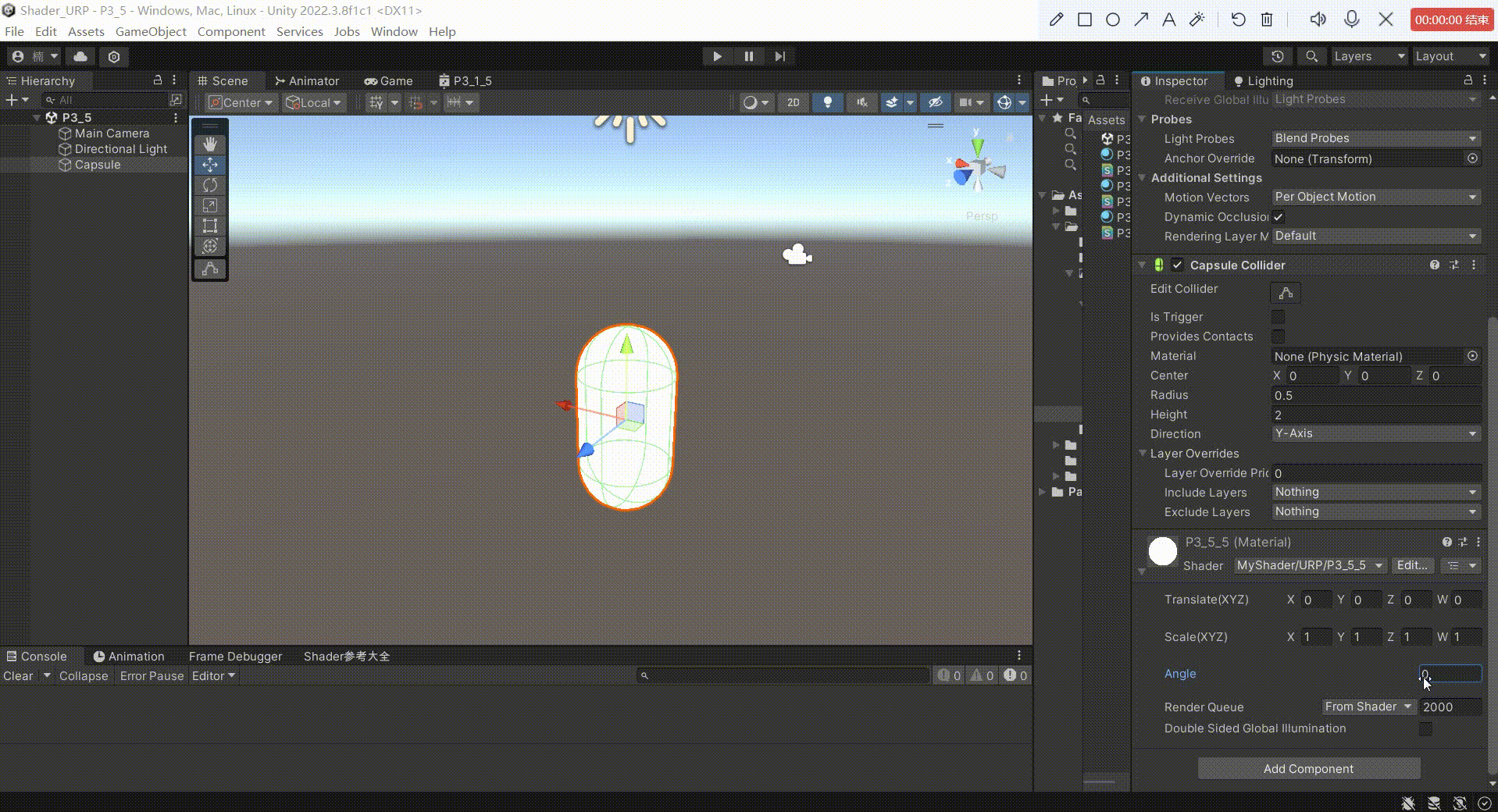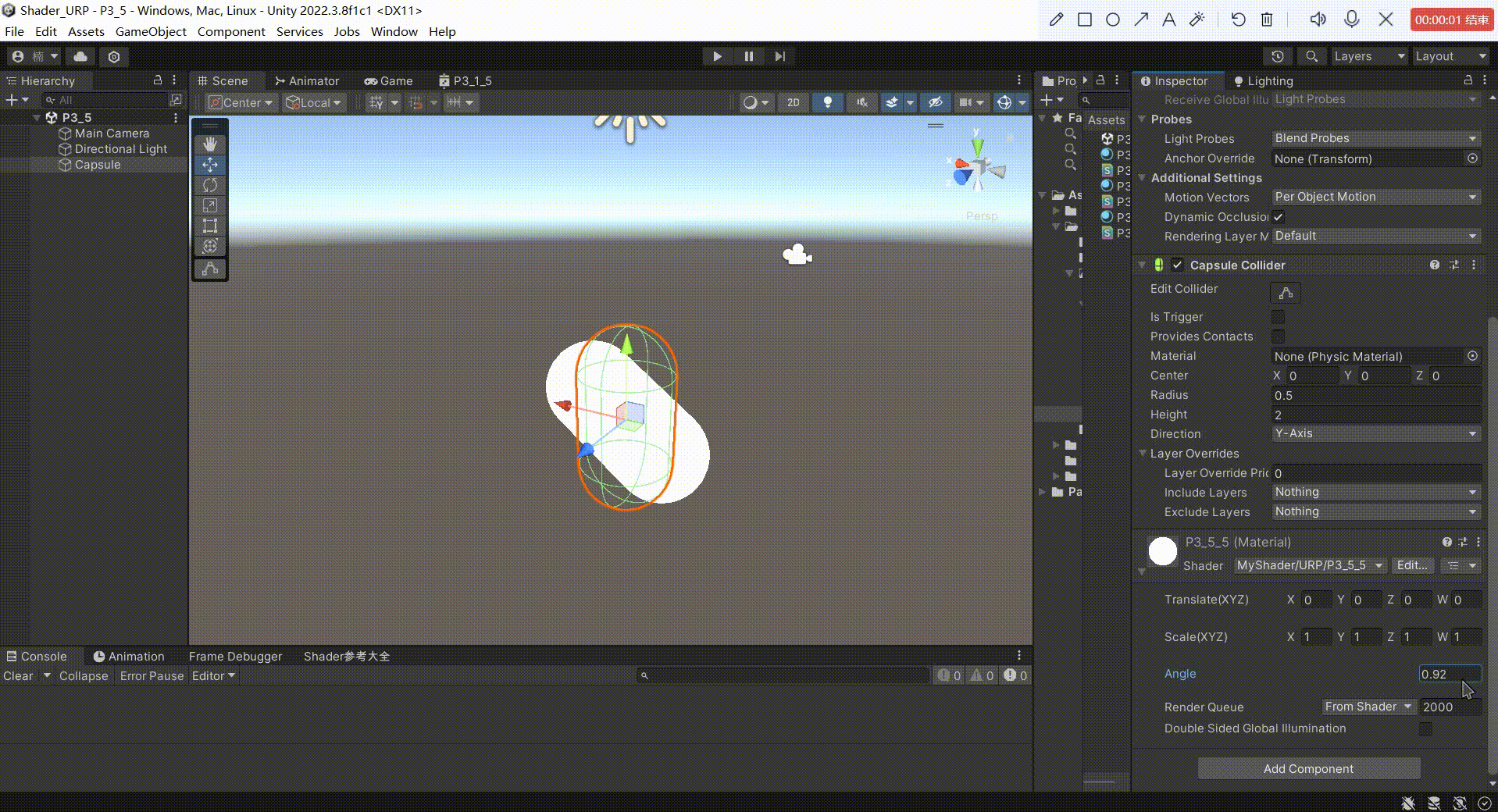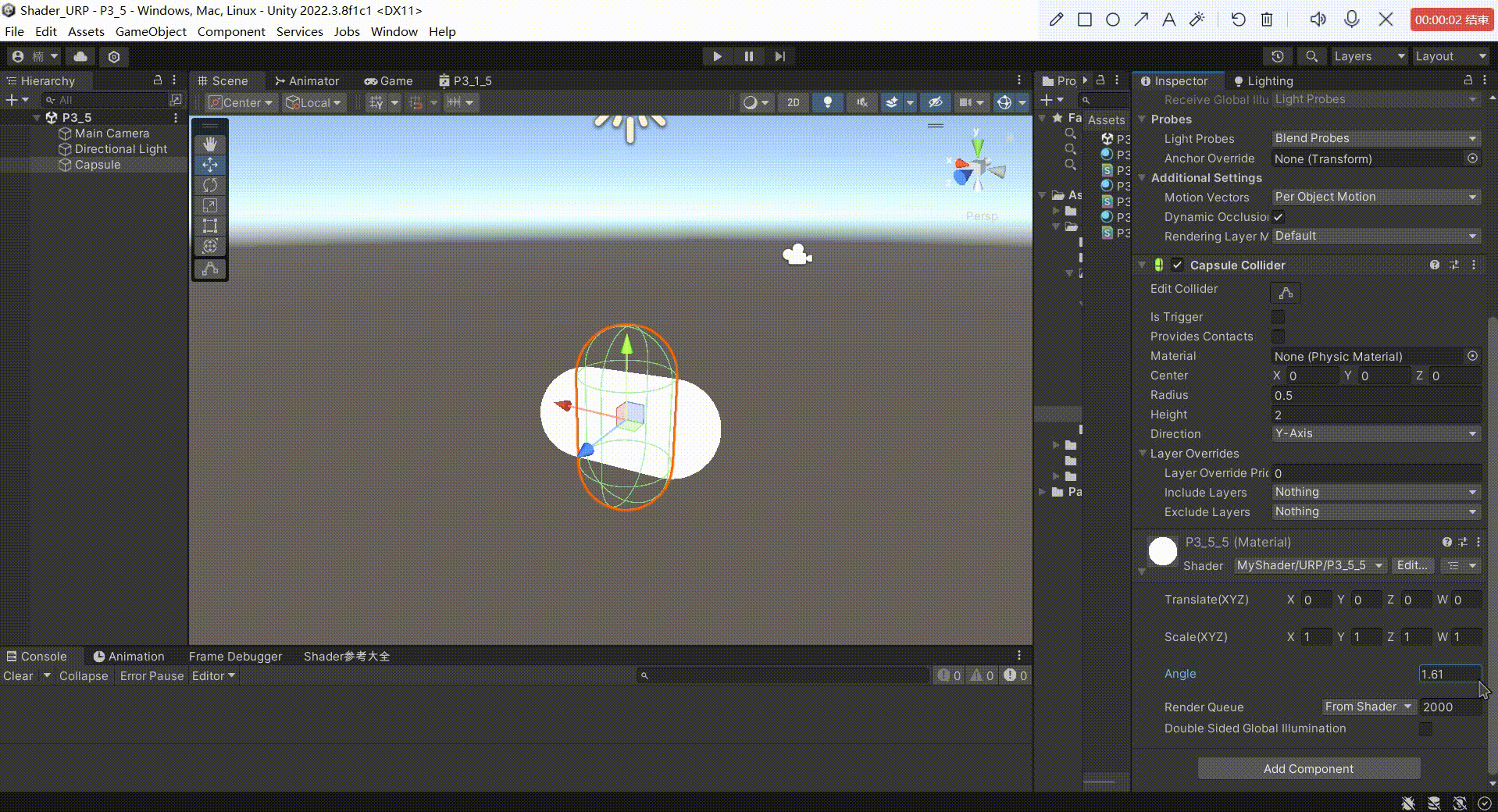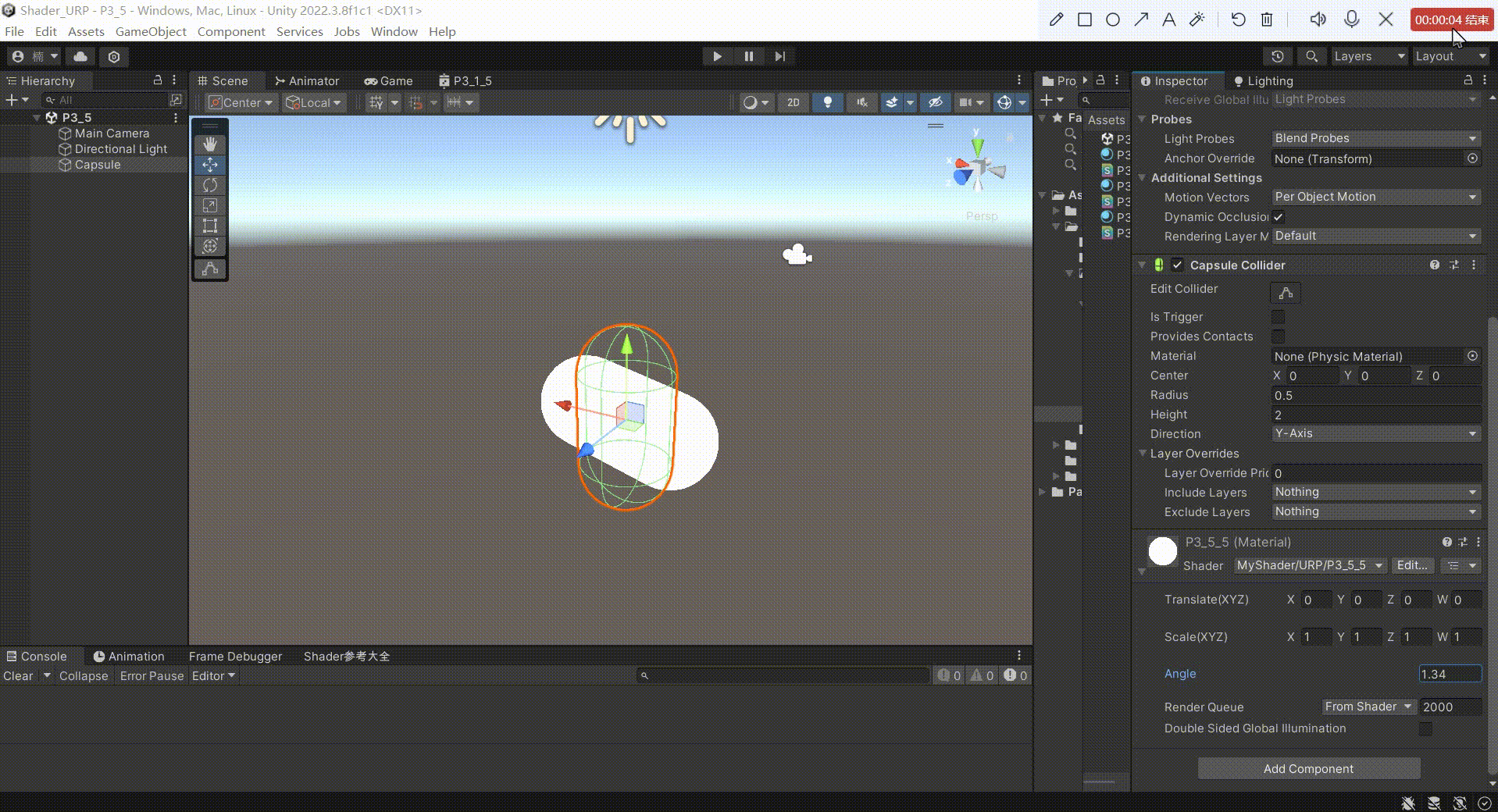
- 三、测试代码
前言
在Shader中,我们经常对顶点进行旋转变换。我们在这篇文章中了解一下旋转使用的旋转矩阵。
一、旋转矩阵的原理
我们先在2D平面下,了解2D原理
1、我们以原点为中心,旋转坐标轴θ度
我们需要求的就是坐标系旋转后,P点在旋转后坐标系中的位置。
因为,我们旋转物体时,我们是围绕着一个轴旋转。
旋转后,我们需要求的就是物体顶点围绕该轴旋转后的坐标位置。
这里我们的 P 点就像 模型的顶点一样,得到P点的位置,就相当于得到了模型顶点在旋转后的位置。
- 旋转前 P1(2,3)
- 旋转后 P2 (?,?)
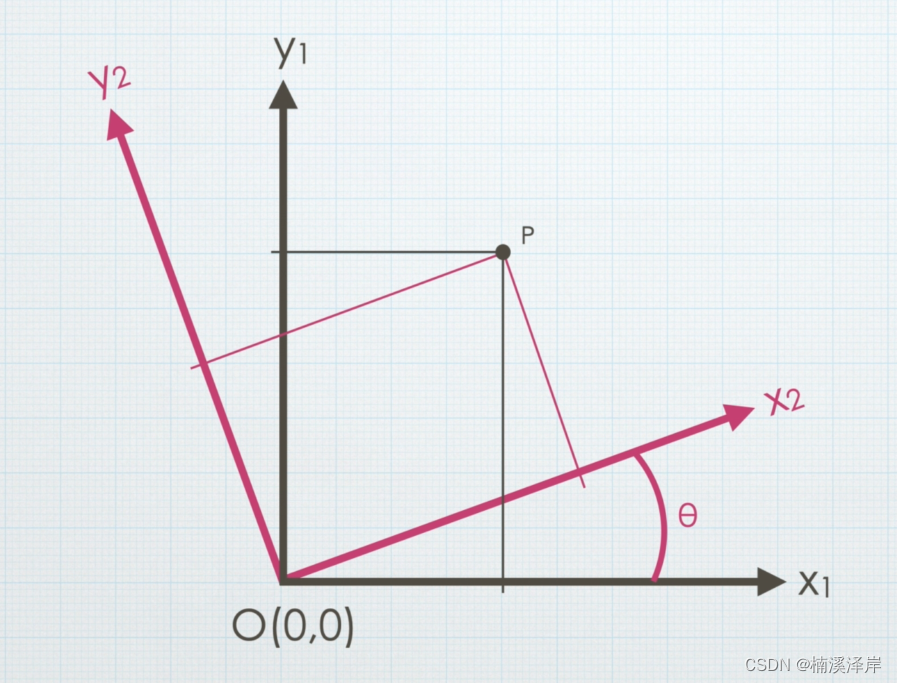
2、求 P2x:
-
求 P2x 可以化为求 OB + BC
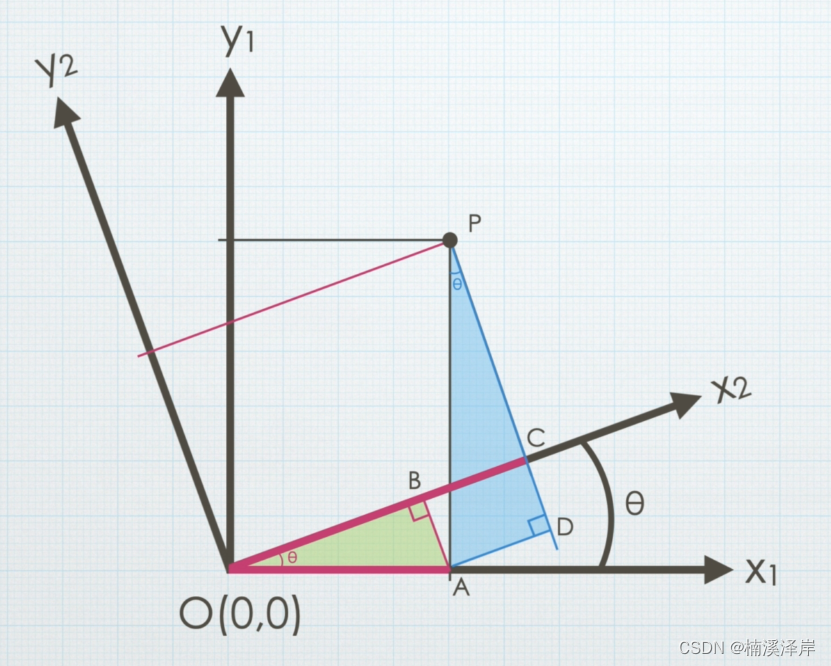
-
求OB:

-
求BC:

-
P2x = OB + BC
P2x = OB + BC = cos(θ)P1x + sin(θ)P1y
3、求P2y:
- 求P2y可以化为求 OC - AC
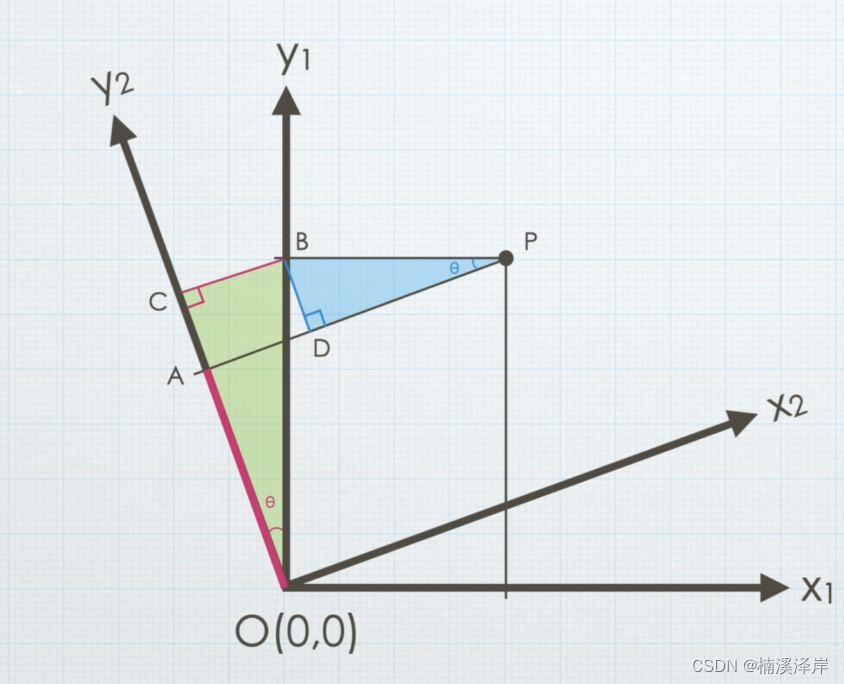
- 求OC:
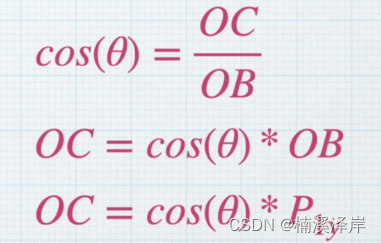
- 求AC:

- P2y = OC - AC
P2y = OC - AC = cos(θ)P1y - sin(θ)P1x
4、最后得到 P2点 的点阵
这个点阵就是我们旋转矩阵的核心
- P2x = OB + BC = cos(θ)P1x + sin(θ)P1y
- P2y = OC - AC = cos(θ)P1y - sin(θ)P1x
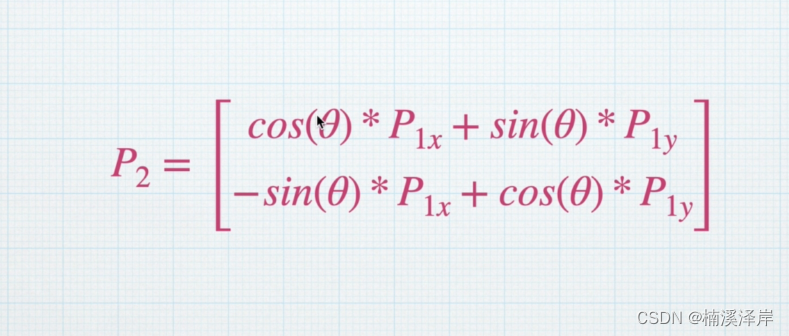
5、该点阵可以拆分为以下两个矩阵相乘的结果
因为,我们该点阵目前是在二维平面旋转。所以,可以认为我们是围绕 z 轴在旋转。
- Mrotate就是我们的旋转矩阵
- P1 就是我们旋转前的点
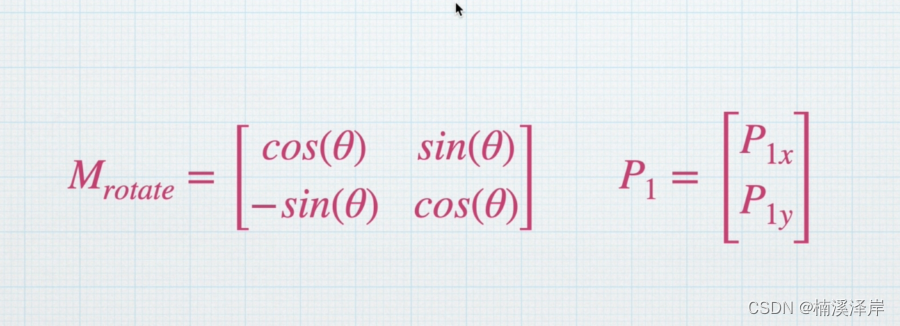
二、在Shader中,使用该旋转矩阵实现围绕 z 轴旋转
1、在属性面板定义 float 变量作为旋转的角度θ
_Angle(“Angle”,Float) = 0
2、在常量缓冲区申明该变量
CBUFFER_START(UnityPerMaterial)
float _Angle;
CBUFFER_END
3、在 顶点着色器 定义旋转矩阵
float2x2 M_rotate = float2x2
(
cos(_Angle),sin(_Angle),
-sin(_Angle),cos(_Angle)
);
4、用旋转矩阵乘以顶点的 xy 实现围绕z轴旋转
v.vertexOS.xy = mul(M_rotate,v.vertexOS.xy);
5、效果
围绕x轴旋转 和 围绕y轴旋转,我们可以修改 .xy 来实现。

三、测试代码
//平移变换
//缩放变换
//旋转变换
Shader "MyShader/URP/P3_5_5"
{Properties{_Translate("Translate(XYZ)",Vector) = (0,0,0,0)_Scale("Scale(XYZ)",Vector)= (1,1,1,1)_Angle("Angle",Float) = 0}SubShader{Tags{"PenderPipeline"="UniversalPipeline""RenderType"="Opaque""Queue"="Geometry"}Pass{HLSLPROGRAM#pragma vertex vert#pragma fragment frag#include "Packages/com.unity.render-pipelines.core/ShaderLibrary/Color.hlsl"#include "Packages/com.unity.render-pipelines.universal/ShaderLibrary/Core.hlsl"#include "Packages/com.unity.render-pipelines.universal/ShaderLibrary/Lighting.hlsl"struct Attribute{float4 vertexOS : POSITION;};struct Varying{float4 vertexCS : SV_POSITION;};CBUFFER_START(UnityPerMaterial)float4 _Translate;float4 _Scale;float _Angle;CBUFFER_ENDVarying vert (Attribute v){Varying o;//平移变换float4x4 M_Translate = float4x4(1,0,0,_Translate.x,0,1,0,_Translate.y,0,0,1,_Translate.z,0,0,0,1);v.vertexOS = mul(M_Translate,v.vertexOS);//缩放交换float4x4 M_Scale = float4x4(_Scale.x,0,0,0,0,_Scale.y,0,0,0,0,_Scale.z,0,0,0,0,1);v.vertexOS = mul(M_Scale,v.vertexOS);//旋转变换float2x2 M_rotate = float2x2(cos(_Angle),sin(_Angle),-sin(_Angle),cos(_Angle));v.vertexOS.xy = mul(M_rotate,v.vertexOS.xy);o.vertexCS = TransformObjectToHClip(v.vertexOS.xyz);return o;}half4 frag (Varying i) : SV_Target{return 1;}ENDHLSL}}
}相关文章:

Unity中Shader旋转矩阵(二维旋转矩阵)
文章目录 前言一、旋转矩阵的原理1、我们以原点为中心,旋转坐标轴θ度2、求 P~2x~:3、求P~2y~:4、最后得到 P~2~点 的点阵5、该点阵可以拆分为以下两个矩阵相乘的结果 二、在Shader中,使用该旋转矩阵实现围绕 z 轴旋转1、在属性面板定义 floa…...
:options请求方法及使用场景)
前端面试题(计算机网络):options请求方法及使用场景
OPTIONS请求方法及使用场景 回答思路:什么是options请求-->options请求方法-->options使用场景什么是options请求?(浅入)扩展:常见的HTTP请求有什么?扩展:常见的HTTP请求的作用࿱…...

使用docker-compose管理docker服务
使用docker-compose管理docker服务 1,创建docker-compose.yml version: 3 services:javaapp:build: context: ./javaappdockerfile: Dockerfileports:- "9202:9202"- "19202:19202"goapp:build: context: ./goappdockerfile: Dockerfileports…...

Python_Tkinter和OpenCV模拟行星凌日传输光度测定
传输光度测定 在天文学中,当相对较小的天体直接经过较大天体的圆盘和观察者之间时,就会发生凌日。 当小物体移过较大物体的表面时,较大物体会稍微变暗。 最著名的凌日是水星和金星对太阳的凌日。 借助当今的技术,天文学家可以在…...

【安全】使用auparse解析auditd审计日志
使用auparse解析auditd审计日志 1 审计日志特点 查看auditd.log的日志,审计日志的格式如下: typeSYSCALL msgaudit(1703148319.954:11680975): archc000003e syscall2 successyes exit5 a01102430 a10 a21b6 a324 items1 ppid7752 pid7761 auid0 uid0…...
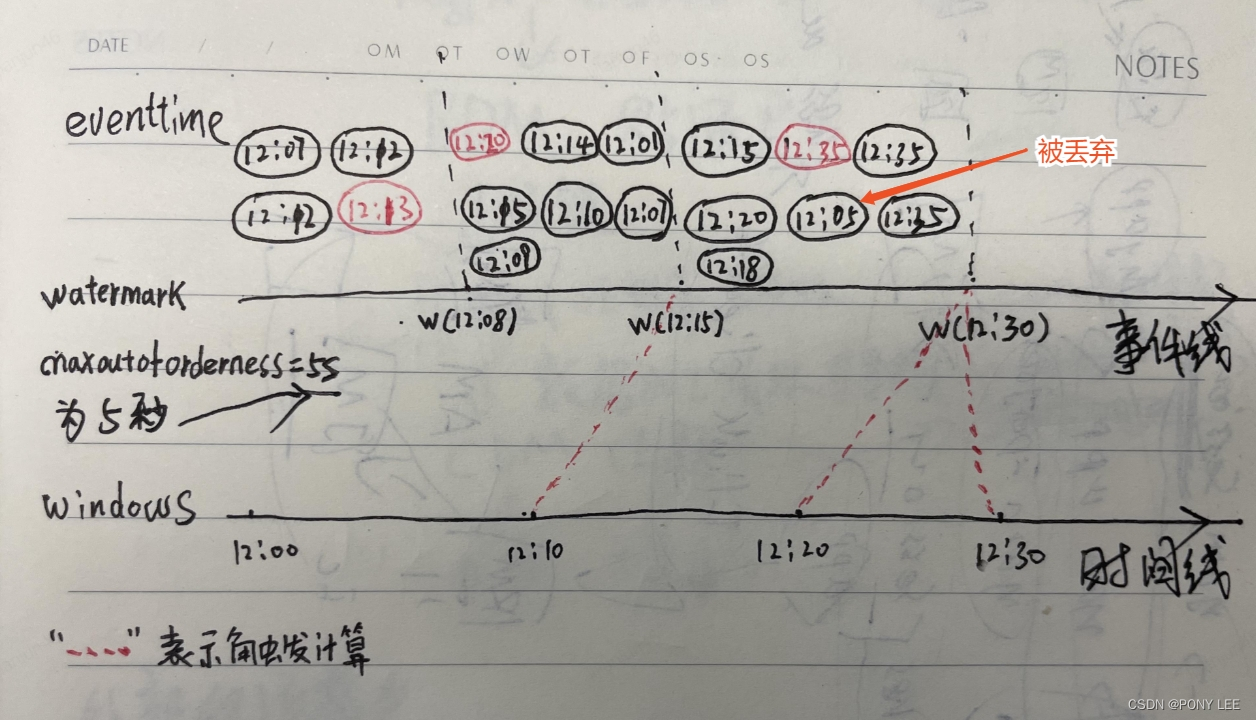
flink watermark 实例分析
WATERMARK 定义了表的事件时间属性,其形式为: WATERMARK FOR rowtime_column_name AS watermark_strategy_expression rowtime_column_name 把一个现有的列定义为一个为表标记事件时间的属性。该列的类型必须为 TIMESTAMP(3)/TIMESTAMP_LTZ(3),且是 sche…...
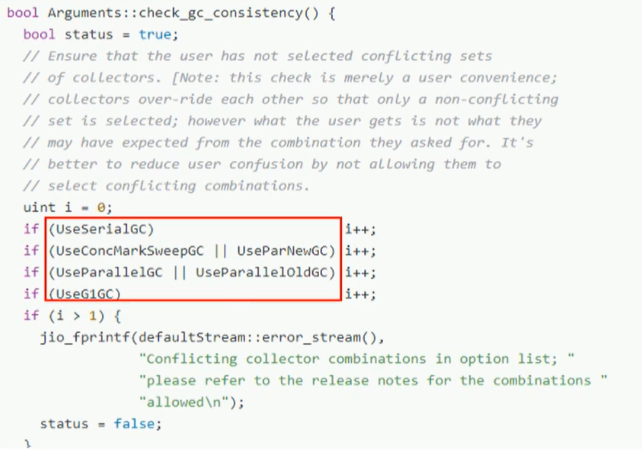
系列十二(面试)、Java中的GC回收类型有哪些?
一、Java中的GC回收类型 1.1、概述 Java中的GC回收类型主要包含以下几种,即:UseSerialGC、UseParallelGC、UseConcMarkSweepGC、UseParNewGC、UseParallelOldGC、UseG1GC。 1.2、源码...

华为数通方向HCIP-DataCom H12-831题库(多选题:201-220)
第201题 在多集群RR组网中,每个集群中部署了一台RR设备及其客户机,各集群的RR与为非客户机关系,并建立IBGP全连接。以下关于BGP路由反射器发布路由规则的描述,正确的有哪些? A、若某RR从EBGP对等体学到的路由,此RR会传递给其他集群的RR B、若某RR从非客户机IBGP对等体学…...
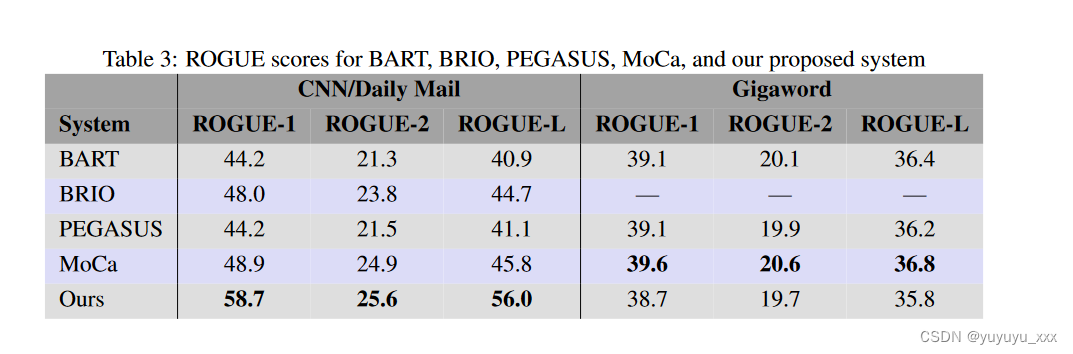
NLP论文阅读记录 - | 使用GPT对大型文档集合进行抽象总结
文章目录 前言0、论文摘要一、Introduction二.相关工作2.1Summarization2.2 神经网络抽象概括2.2.1训练和测试数据集。2.2.2 评估。 2.3 最先进的抽象摘要器 三.本文方法3.1 查询支持3.2 文档聚类3.3主题句提取3.4 语义分块3.5 GPT 零样本总结 四 实验效果4.1数据集4.2 对比模型…...
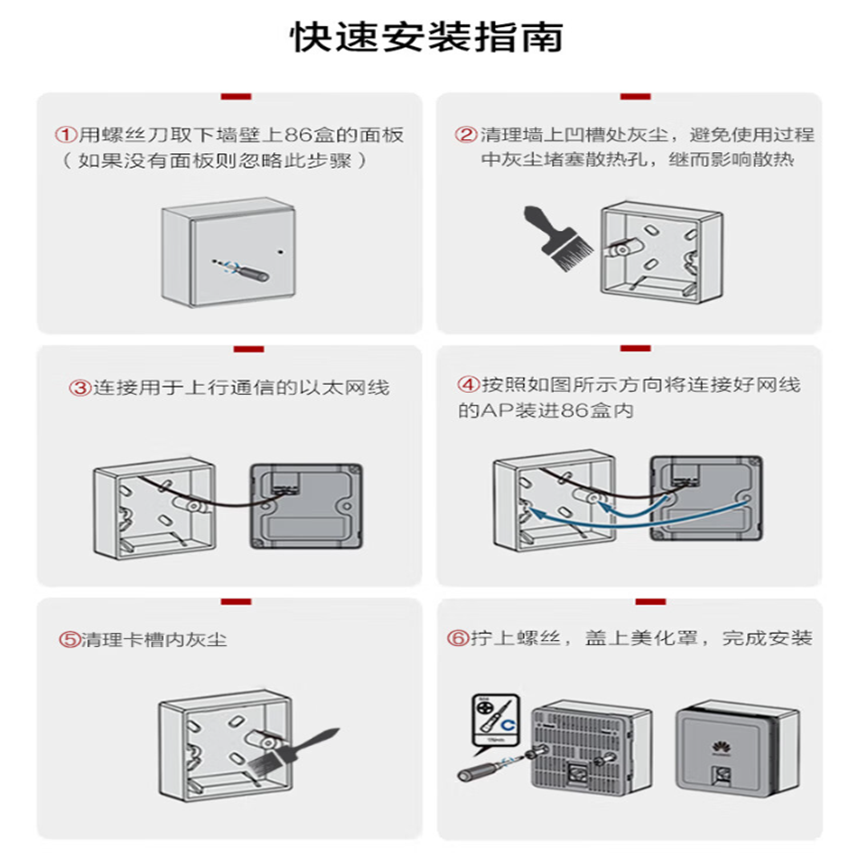
华为全屋wifi6蜂鸟套装标准
华为政企42 华为政企 目录 上一篇华为安防监控摄像头下一篇华为企业级无线路由器...
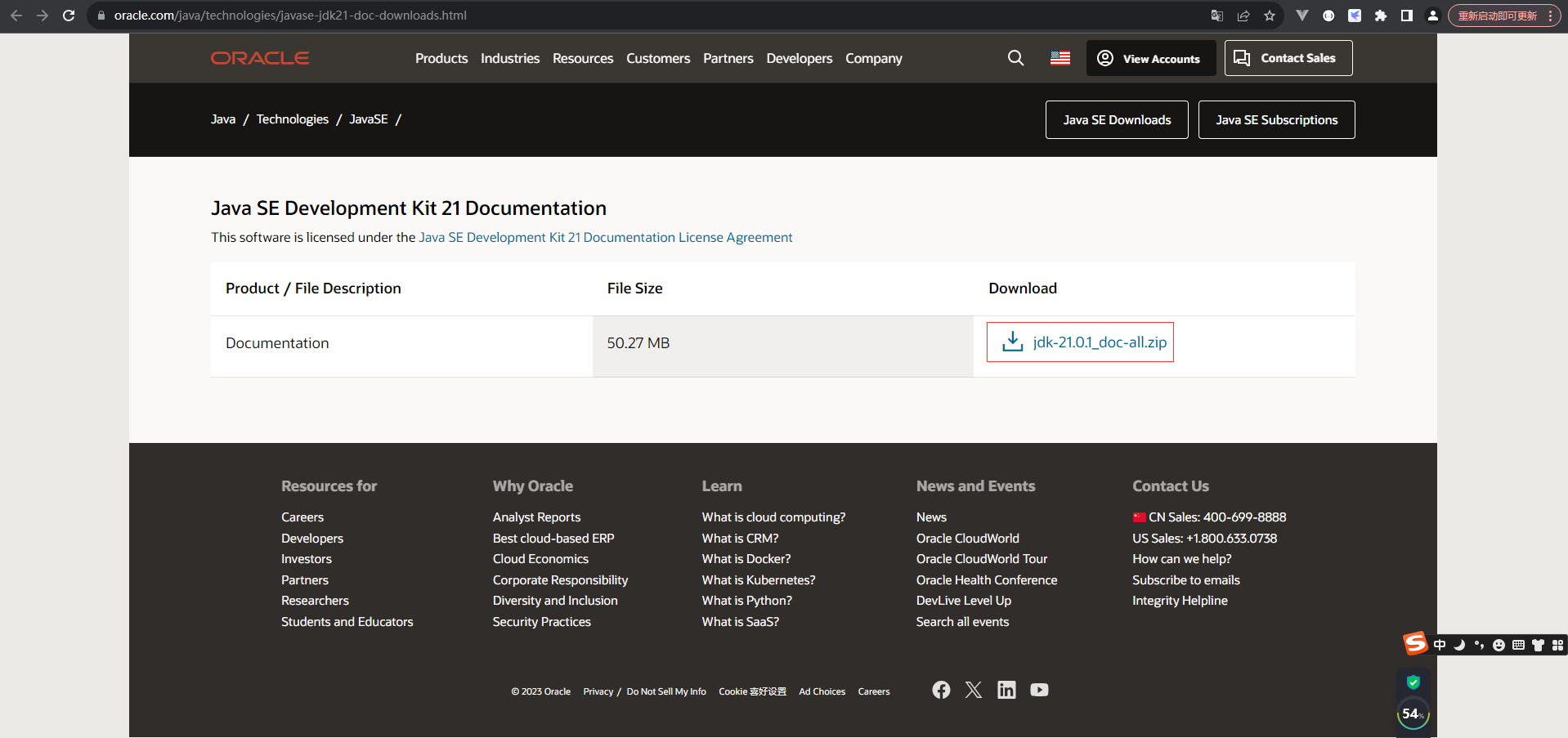
系列二十八、如何在Oracle官网下载JDK的api文档
一、官网下载JDK的api文档 1.1、官网地址 https://www.oracle.com/java/technologies/javase-jdk21-doc-downloads.html 1.2、我分享的api.chm 链接:https://pan.baidu.com/s/1Bf55Fz-eMTErmQDtZZcewQ?pwdyyds 提取码:yyds 1.3、参考 https://ww…...
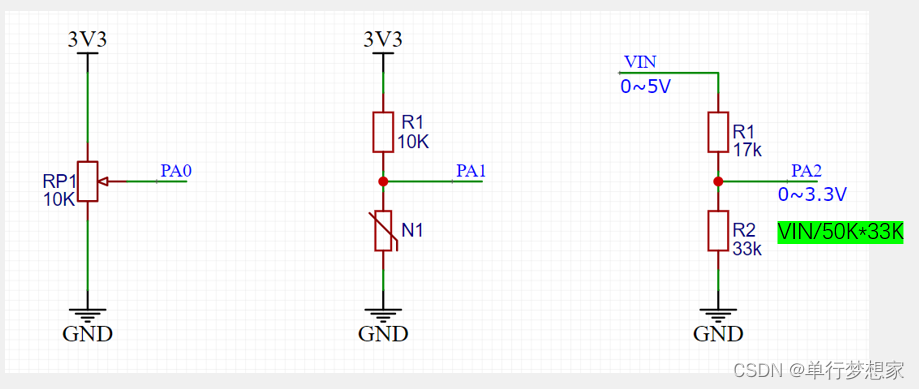
STM32-ADC模数转换器
目录 一、ADC简介 二、逐次逼近型ADC内部结构 三、STM32内部ADC转换结构 四、ADC基本结构 五、输入通道 六、转换模式 6.1单次转换,非扫描模式 6.2连续转换,非扫描模式 6.3单次转换,扫描模式 6.4连续转换,扫描模式 七、…...
谷歌手机安装证书到根目录
1、前提你已经root,安装好面具 2,下载movecert模块,自动帮你把证书从用户证书移动成系统证书 视频教程,手机为谷歌手机 https://www.bilibili.com/video/BV1pG4y1A7Cj?p11&vd_source9c0a32b00d6d59fecae05b4133f22f06 软件下…...

代码随想录 322. 零钱兑换
题目 给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。 计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。 你可以认为每种硬币的数量是无限的。…...

【图的应用二:最短路径】- 用 C 语言实现迪杰斯特拉算法和弗洛伊德算法
目录 一、最短路径 二、迪杰斯特拉算法 三、弗洛伊德算法 一、最短路径 假若要在计算机上建立一个交通咨询系统,则可以采用图的结构来表示实际的交通网络。如下图所示,图中顶点表示城市,边表示城市间的交通联系。 这个咨询系统可以回答旅…...
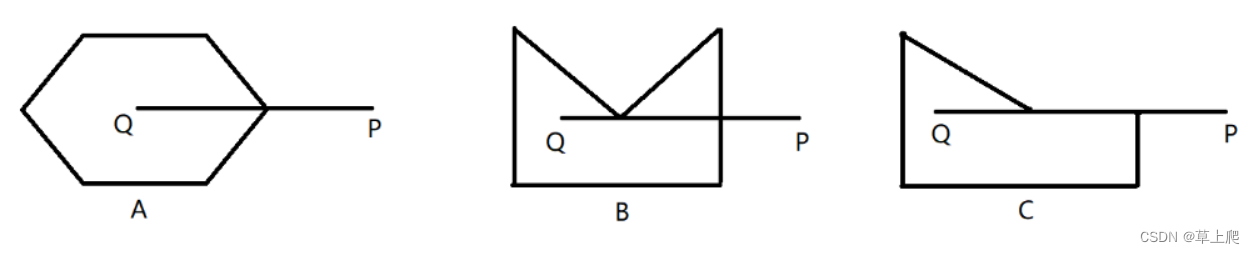
Qt之判断一个点是否在多边形内部(射线法)
算法思想: 以被测点Q为端点,向任意方向作射线(一般水平向右作射线),统计该射线与多边形的交点数。如果为奇数,Q在多边形内;如果为偶数,Q在多边形外。计数的时候会有一些特殊情况。这种方法适用于任意多边形,不需要考虑精度误差和多边形点给出的顺序,时间复杂度为O(n)…...
情况如何解决)
压力测试过程中内存溢出(堆溢出、栈溢出、持久代溢出)情况如何解决
在压力测试过程中,可能会遇到内存溢出的问题,其中常见的包括堆内存溢出、栈内存溢出和持久代溢出。解决这类问题需要首先理解各种内存溢出的原因和特点。 堆内存溢出:这种情况通常发生在稳定性压测一段时间后,系统报错࿰…...

【工业智能】音频信号相关场景
【工业智能】音频信号相关场景 DcaseDcase introduction:dcase2024有10个主题的任务: ASD硬件设备产品商 方法制造业应用场景 zenodo音频事件检测 与计算机视觉CV相对应,计算机听觉computer audition,简称CA。 Dcase 这里推荐一个…...
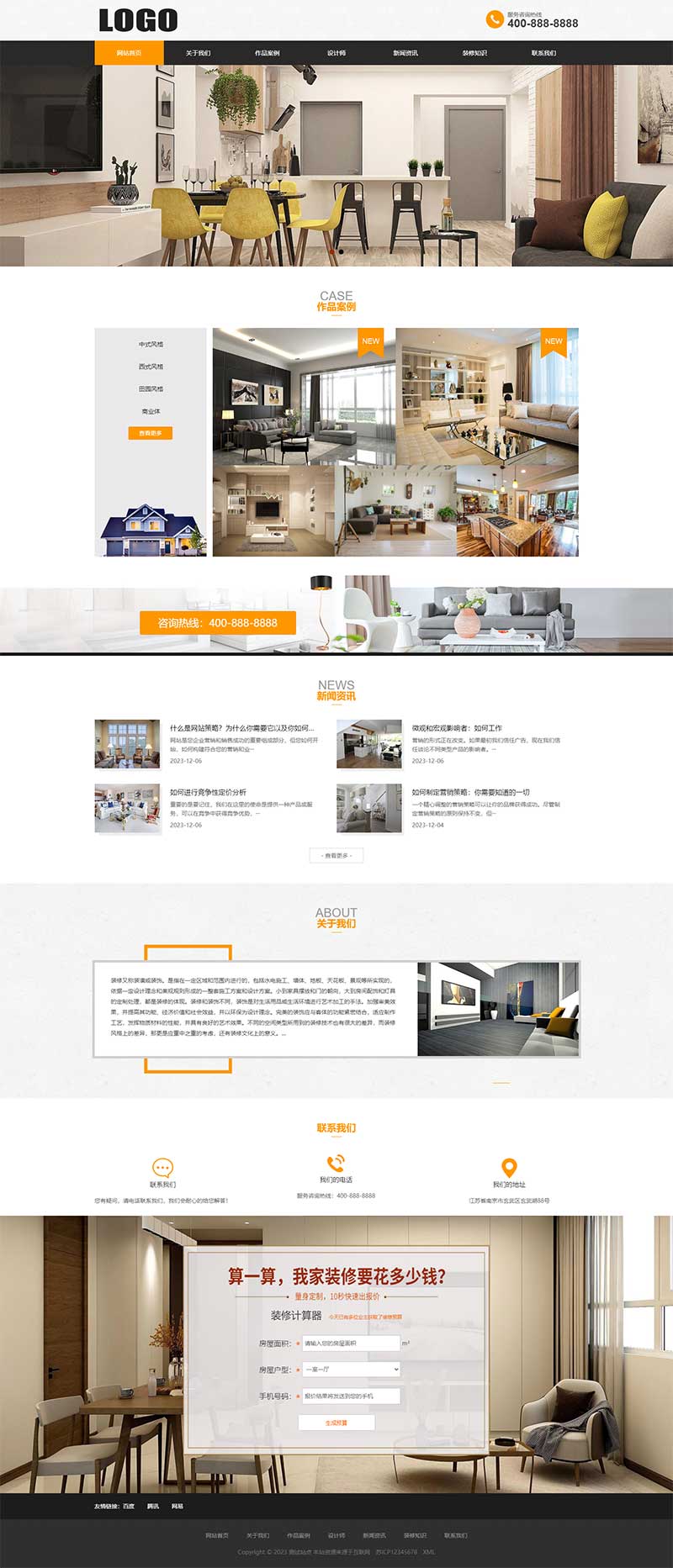
(PC+WAP)装修设计公司网站模板 家装公司网站源码下载
(PCWAP)装修设计公司网站模板 家装公司网站源码下载 PbootCMS内核开发的网站模板,该模板适用于装修设计、家装公司类等企业,当然其他行业也可以做,只需要把文字图片换成其他行业的即可; PCWAP,同一个后台,…...

使用opencv实现图像中几何图形检测
1 几何图形检测介绍 1.1 轮廓(contours) 什么是轮廓,简单说轮廓就是一些列点相连组成形状、它们拥有同样的颜色、轮廓发现在图像的对象分析、对象检测等方面是非常有用的工具,在OpenCV 中使用轮廓发现相关函数时候要求输入图像是二值图像,这…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...
