机器学习 | 聚类Clustering 算法
物以类聚人以群分。
什么是聚类呢?

1、核心思想和原理
聚类的目的
同簇高相似度
不同簇高相异度
同类尽量相聚
不同类尽量分离
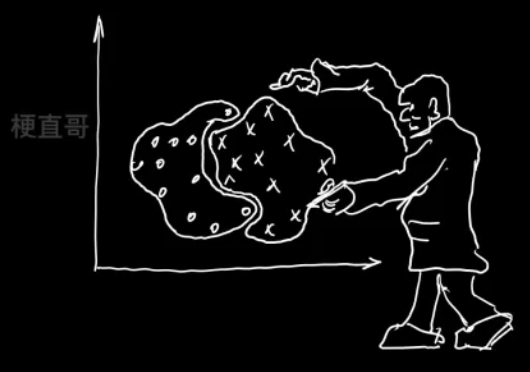
聚类和分类的区别
分类 classification
监督学习
训练获得分类器
预测未知数据
聚类 clustering
无监督学习,不关心类别标签
没有训练过程
算法自己要根据定义的规则将相似的样本划分到一起,不相似的样本分成不同的类别,不同的簇
簇 Cluster
簇内样本之间的距离,或样本点在数据空间的密度
对簇的不同定义可以得到不同的算法

主要聚类方法

聚类步骤
- 数据准备:特征的标准化和降维
- 特征选择:最有效特征,并将其存储在向量当中
- 特征提取:特征转换,通过对选择的特征进行一些转换,形成更突出的特征
- 聚类:基于某种距离做相似度度量,得到簇
- 结果评估:分析聚类结果
2、K-means和分层聚类
2.1、基于划分的聚类方式
将对象划分为互斥的簇
每个对象仅属于一个簇
簇间相似性低,簇内相似性高
K-均值分类
根据样本点与簇质心距离判定
以样本间距离衡量簇内相似度
回顾一下

K均值聚类算法步骤:
- 选择k个初始质心,初始质心的选择是随机的,每一个质心是一个类
- 计算样本到各个质心欧式距离,归入最近的簇
- 计算新簇的质心,重复2 3,直到质心不再发生变化或者达到最大迭代次数
2.2、层次聚类
按照层次把数据划分到不同层的簇,形成树状结构,可以揭示数据间的分层结构
在树形结构上不同层次划分可以得到不同粒度的聚类
过程分为自底向上的聚合聚类和自顶向下的分裂聚类
自底向上的聚合聚类
将每个样本看做一个簇,初始状态下簇的数目 = 样本的数目
簇间距离最小的相似簇合并
下图纵轴不是合并的次序,而是合并的距离
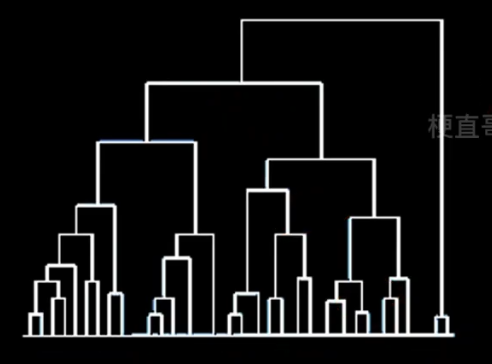
簇间距离(簇间相似度)的度量
第一种 即使已经离得很近,可能也老死不能合并。
第二种 可能出现 链条式 的效果。
第三种 相对合适。

自顶向下的分裂聚类
所有样本看成一个簇
逐渐分裂成更小的簇
目前大多数聚类算法使用的都是自底向上的聚合聚类方法
3、聚类算法代码实现
import numpy as np
import matplotlib.pyplot as pltfrom sklearn.datasets import make_blobs
X, y = make_blobs(n_samples=250, centers=5, n_features=2, random_state=0)
plt.scatter(X[:,0], X[:,1], c=y)
plt.show()
plt.scatter(X[:,0], X[:,1])
plt.show()
KMeans 聚类法
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=5, random_state=0).fit(X)此处设定簇的个数为5
kmeans.labels_注意,聚类不是分类,0-4只是相当于五个小组,治愈每个组是什么类型并不知道。
array([4, 4, 0, 1, 2, 0, 1, 0, 3, 2, 4, 0, 3, 2, 1, 2, 2, 4, 2, 0, 0, 0,4, 1, 1, 1, 0, 3, 4, 1, 0, 0, 2, 3, 4, 2, 2, 4, 2, 2, 4, 3, 1, 0,0, 3, 3, 2, 0, 1, 0, 1, 1, 1, 3, 2, 3, 4, 0, 0, 0, 3, 2, 3, 3, 0,4, 3, 4, 0, 0, 2, 4, 2, 1, 0, 2, 1, 1, 4, 1, 4, 0, 3, 2, 0, 3, 4,2, 3, 0, 3, 1, 0, 4, 1, 3, 2, 0, 2, 4, 3, 2, 0, 3, 3, 0, 4, 3, 0,0, 3, 3, 1, 3, 1, 0, 2, 3, 4, 4, 0, 2, 4, 3, 3, 4, 2, 2, 3, 4, 4,0, 2, 2, 4, 0, 1, 3, 3, 2, 0, 2, 1, 2, 3, 2, 0, 4, 0, 1, 0, 4, 3,1, 3, 3, 1, 3, 2, 2, 1, 1, 0, 1, 4, 0, 1, 2, 3, 3, 4, 2, 2, 0, 4,4, 1, 4, 2, 1, 3, 1, 1, 0, 4, 3, 1, 2, 1, 1, 2, 3, 4, 4, 2, 1, 2,1, 3, 4, 2, 1, 1, 1, 4, 3, 2, 0, 4, 3, 3, 2, 0, 3, 4, 4, 0, 3, 4,3, 2, 0, 1, 3, 3, 0, 0, 2, 2, 0, 2, 2, 1, 0, 1, 1, 4, 4, 1, 2, 1,4, 1, 4, 3, 4, 3, 1, 1], dtype=int32)
plt.scatter(X[:,0], X[:,1], c=kmeans.labels_)<matplotlib.collections.PathCollection at 0x7f3285fb57c0>

center = kmeans.cluster_centers_
centerarray([[ 0.93226669, 4.273606 ],[ 9.27996402, -2.3764533 ],[ 2.05849588, 0.9767519 ],[-1.39550161, 7.57857088],[-1.85199006, 2.98013351]])
plt.scatter(X[:,0], X[:,1], c=kmeans.labels_)
center = kmeans.cluster_centers_
plt.scatter(center[:,0],center[:,1], marker='x', c = 'red')
plt.show()
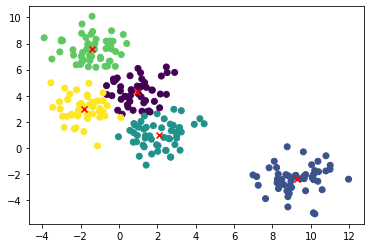
for n_clusters in [2, 3, 4, 5, 6, 7]:clusterer = KMeans(n_clusters=n_clusters, random_state=0).fit(X)z = clusterer.labels_center = clusterer.cluster_centers_plt.scatter(X[:,0], X[:,1], c=z)plt.scatter(center[:,0], center[:,1],marker = 'x', c='red')plt.title("k: {0}".format(n_clusters))plt.show()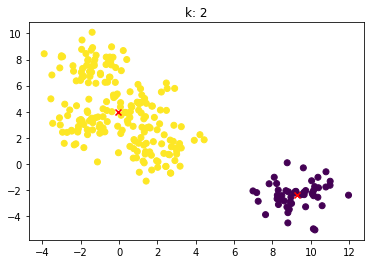

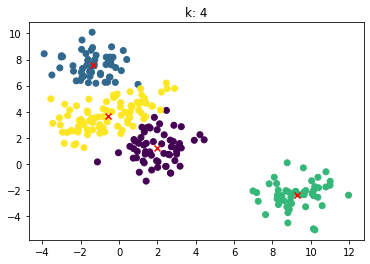


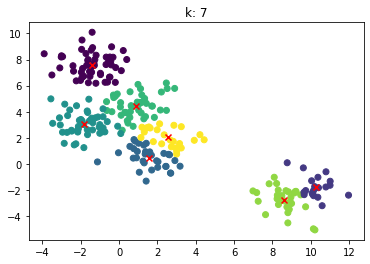
层次聚类法 没有聚类中心
from sklearn.cluster import AgglomerativeClustering
agg = AgglomerativeClustering(linkage='ward', n_clusters=5).fit(X)plt.scatter(X[:,0], X[:,1], c=agg.labels_)
plt.show()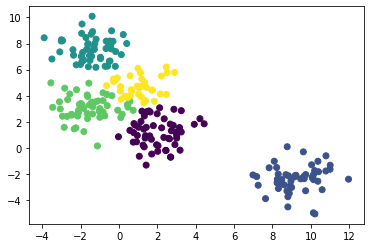
当我们对簇的个数没有预期时,不要一个一个试,可以传入距离的阈值。
agg = AgglomerativeClustering(distance_threshold=10, n_clusters=None).fit(X)
plt.scatter(X[:,0], X[:,1], c=agg.labels_)
plt.show()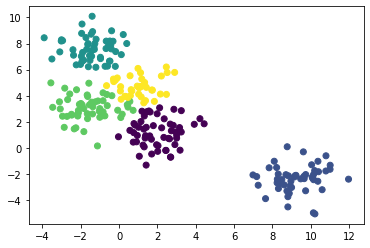
from scipy.cluster.hierarchy import linkage, dendrogram
def show_dendrogram(model):counts = np.zeros(model.children_.shape[0])n_samples = len(model.labels_)for i, merge in enumerate(model.children_):current_count = 0for child_idx in merge:if child_idx < n_samples:current_count += 1 # leaf nodeelse:current_count += counts[child_idx - n_samples]counts[i] = current_countlinkage_matrix = np.column_stack([model.children_, model.distances_, counts]).astype(float)dendrogram(linkage_matrix)show_dendrogram(agg)
import time
import warningsfrom sklearn import cluster, datasets
from sklearn.preprocessing import StandardScaler
from itertools import cycle, islice
n_samples = 1500
noisy_circles = datasets.make_circles(n_samples=n_samples, factor=0.5, noise=0.05)
noisy_moons = datasets.make_moons(n_samples=n_samples, noise=0.05)
blobs = datasets.make_blobs(n_samples=n_samples, random_state=8)
no_structure = np.random.rand(n_samples, 2), None# Anisotropicly distributed data
random_state = 170
X, y = datasets.make_blobs(n_samples=n_samples, random_state=random_state)
transformation = [[0.6, -0.6], [-0.4, 0.8]]
X_aniso = np.dot(X, transformation)
aniso = (X_aniso, y)# blobs with varied variances
varied = datasets.make_blobs(n_samples=n_samples, cluster_std=[1.0, 2.5, 0.5], random_state=random_state
)# Set up cluster parameters
plt.figure(figsize=(9 * 1.3 + 2, 14.5))
plt.subplots_adjust(left=0.02, right=0.98, bottom=0.001, top=0.96, wspace=0.05, hspace=0.01
)plot_num = 1default_base = {"n_neighbors": 10, "n_clusters": 3}datasets = [(noisy_circles, {"n_clusters": 2}),(noisy_moons, {"n_clusters": 2}),(varied, {"n_neighbors": 2}),(aniso, {"n_neighbors": 2}),(blobs, {}),(no_structure, {}),
]for i_dataset, (dataset, algo_params) in enumerate(datasets):# update parameters with dataset-specific valuesparams = default_base.copy()params.update(algo_params)X, y = dataset# normalize dataset for easier parameter selectionX = StandardScaler().fit_transform(X)# ============# Create cluster objects# ============ward = cluster.AgglomerativeClustering(n_clusters=params["n_clusters"], linkage="ward")complete = cluster.AgglomerativeClustering(n_clusters=params["n_clusters"], linkage="complete")average = cluster.AgglomerativeClustering(n_clusters=params["n_clusters"], linkage="average")single = cluster.AgglomerativeClustering(n_clusters=params["n_clusters"], linkage="single")clustering_algorithms = (("Single Linkage", single),("Average Linkage", average),("Complete Linkage", complete),("Ward Linkage", ward),)for name, algorithm in clustering_algorithms:t0 = time.time()# catch warnings related to kneighbors_graphwith warnings.catch_warnings():warnings.filterwarnings("ignore",message="the number of connected components of the "+ "connectivity matrix is [0-9]{1,2}"+ " > 1. Completing it to avoid stopping the tree early.",category=UserWarning,)algorithm.fit(X)t1 = time.time()if hasattr(algorithm, "labels_"):y_pred = algorithm.labels_.astype(int)else:y_pred = algorithm.predict(X)plt.subplot(len(datasets), len(clustering_algorithms), plot_num)if i_dataset == 0:plt.title(name, size=18)colors = np.array(list(islice(cycle(["#377eb8","#ff7f00","#4daf4a","#f781bf","#a65628","#984ea3","#999999","#e41a1c","#dede00",]),int(max(y_pred) + 1),)))plt.scatter(X[:, 0], X[:, 1], s=10, color=colors[y_pred])plt.xlim(-2.5, 2.5)plt.ylim(-2.5, 2.5)plt.xticks(())plt.yticks(())plt.text(0.99,0.01,("%.2fs" % (t1 - t0)).lstrip("0"),transform=plt.gca().transAxes,size=15,horizontalalignment="right",)plot_num += 1plt.show()
4、聚类评估代码实现
聚类效果评估方法
已知标签评价
调整兰德指数Adjusted Rand lndex
调整互信息分Adjusted mutual info score
基于预测簇向量与真实簇向量的互信息分数
V-Measure
同质性和完整性的调和平均值
————取值在-1到1,越接近1越好
未知标签评价
轮廓系数
通过计算样本与所在簇中其他样本的相似度
CHI (Calinski-Harabaz lndex/Variance Ratio Criterion)
群间离散度和群内离散度的比例
代码实现
import numpy as np
import matplotlib.pyplot as pltfrom sklearn.datasets import make_blobs
X, y = make_blobs(n_samples=250, n_features=2, centers=5, random_state=0)from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=5, random_state=0).fit(X)
z = kmeans.labels_center = kmeans.cluster_centers_
plt.scatter(X[:,0], X[:,1], c=z)
plt.scatter(center[:,0], center[:,1], marker = 'x', c='red')
plt.show()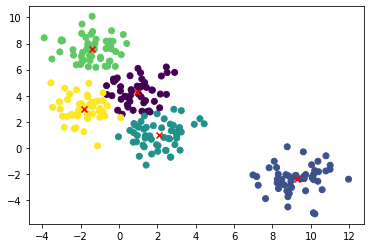
已知标签
from sklearn.metrics import adjusted_rand_score
adjusted_rand_score(y,z)0.8676297613641788
from sklearn.metrics import adjusted_mutual_info_score
adjusted_mutual_info_score(y,z)0.8579576361507845
from sklearn.metrics import v_measure_score
v_measure_score(y,z)0.8608558483955058
ari_curve = []
ami_curve = []
vm_curve = []
clus = [2, 3, 4, 5, 6, 7]
for n_clusters in clus:clusterer = KMeans(n_clusters=n_clusters, random_state=0).fit(X)z = clusterer.labels_ari_curve.append(adjusted_rand_score(y,z))ami_curve.append(adjusted_mutual_info_score(y,z))vm_curve.append(v_measure_score(y,z))plt.plot(clus, ari_curve, label='ari')
plt.plot(clus, ami_curve, label='ami')
plt.plot(clus, vm_curve, label='vm')
plt.legend()
plt.show()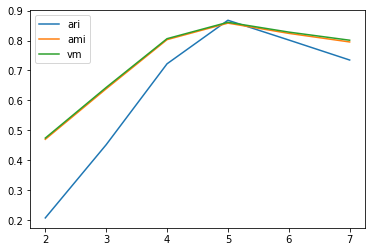
未知标签
from sklearn.metrics import silhouette_score
kmeans = KMeans(n_clusters=5, random_state=0).fit(X)
cluster_labels = kmeans.labels_
si = silhouette_score(X, cluster_labels)
si0.5526930597314647
from sklearn.metrics import silhouette_samples
import matplotlib.cm as cmdef show_silhouette_plot(model, X):for n_clusters in [2, 3, 4, 5, 6, 7]:fig, (pic1, pic2) = plt.subplots(1, 2)fig.set_size_inches(15, 5)model.n_clusters = n_clustersclusterer = model.fit(X)cluster_labels = clusterer.labels_centers = clusterer.cluster_centers_silhouette_avg = silhouette_score(X, cluster_labels)sample_silhouette_values = silhouette_samples(X, cluster_labels)y_lower = 1for i in range(n_clusters):ith_cluster_silhouette_values = sample_silhouette_values[cluster_labels == i]ith_cluster_silhouette_values.sort()size_cluster_i = ith_cluster_silhouette_values.shape[0]y_upper = y_lower + size_cluster_icolor = cm.nipy_spectral(float(i) / n_clusters)pic1.fill_betweenx(np.arange(y_lower, y_upper), ith_cluster_silhouette_values, facecolor = color)pic1.text(-0.02, y_lower + 0.5 * size_cluster_i, str(i))y_lower = y_upper + 1pic1.axvline(x = silhouette_avg, color = 'red', linestyle = "--")pic1.set_title("score: {0}".format(silhouette_avg))colors = cm.nipy_spectral(cluster_labels.astype(float) / n_clusters)pic2.scatter(X[:,0], X[:,1], marker = 'o', c = colors)pic2.scatter(centers[:, 0], centers[:, 1], marker = 'x', c = 'red', alpha = 1, s = 200)pic2.set_title("k: {0}".format(n_clusters))show_silhouette_plot(kmeans, X)


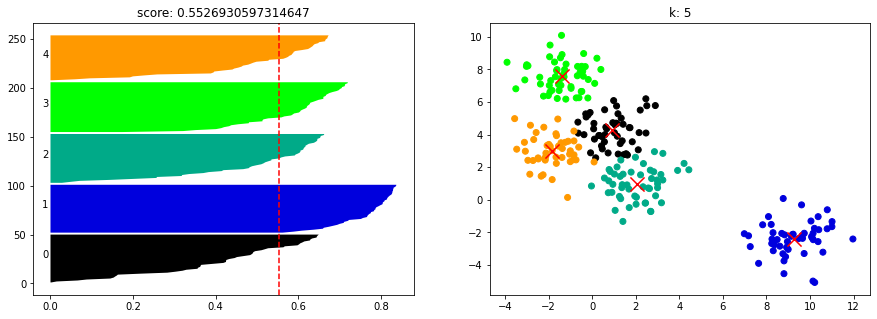


from sklearn.metrics import calinski_harabasz_score
calinski_harabasz_score(X, y)850.6346471314978
chi_curve = []clus = [2, 3, 4, 5, 6, 7]
for n_clusters in clus:clusterer = KMeans(n_clusters=n_clusters, random_state=0).fit(X)z = clusterer.labels_chi_curve.append(calinski_harabasz_score(X,z))plt.plot(clus, chi_curve, label='chi')
plt.legend()
plt.show()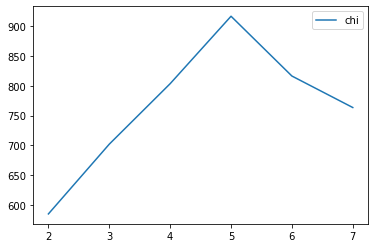
5、优缺点和适用条件
K--means聚类优缺点
优点
算法简单,收敛速度快
簇间区别大时效果好
对大数据集,算法可伸缩性强(可伸缩性:但数据从几百上升到几百万时,聚类结果的准确度/一致性 特别好)
缺点
簇数k难以估计
对初始聚类中心敏感
容易陷入局部最优
簇不规则时,容易对大簇分割(当采用误差平方和的准则作为聚类准则函数,如果各类的大小或形状差距很大时,有可能出现将大类分割的现象)
‘
’K--means聚类适用条件
簇是密集的、球状或团状
簇与簇间区别明显
簇本身数据比较均匀
适用大数据集
凸性簇
分层聚类优缺点
优点
距离相似度容易定义限制少
无需指定簇数
可以发现簇的层次关系
缺点
由于要计算邻近度矩阵,对时间和空间需求大
困难在于合并或分裂点的选择
可拓展性差
分层聚类适用条件
适合于小型数据集的聚类
可以在不同粒度水平上对数据进行探测,发现簇间层次关系
参考
Machine-Learning: 《机器学习必修课:经典算法与Python实战》配套代码 - Gitee.com
相关文章:

机器学习 | 聚类Clustering 算法
物以类聚人以群分。 什么是聚类呢? 1、核心思想和原理 聚类的目的 同簇高相似度 不同簇高相异度 同类尽量相聚 不同类尽量分离 聚类和分类的区别 分类 classification 监督学习 训练获得分类器 预测未知数据 聚类 clustering 无监督学习,不关心类别标签 …...
IntelliJ IDEA 2023.3 新功能介绍
IntelliJ IDEA 2023.3 在众多领域进行了全面的改进,引入了许多令人期待的功能和增强体验。以下是该版本的一些关键亮点: IntelliJ IDEA mac版下载 macappbox.com/a/intellij-idea-for-mac.html 1. AI Assistant 的全面推出 IntelliJ IDEA 2023.3 中&am…...
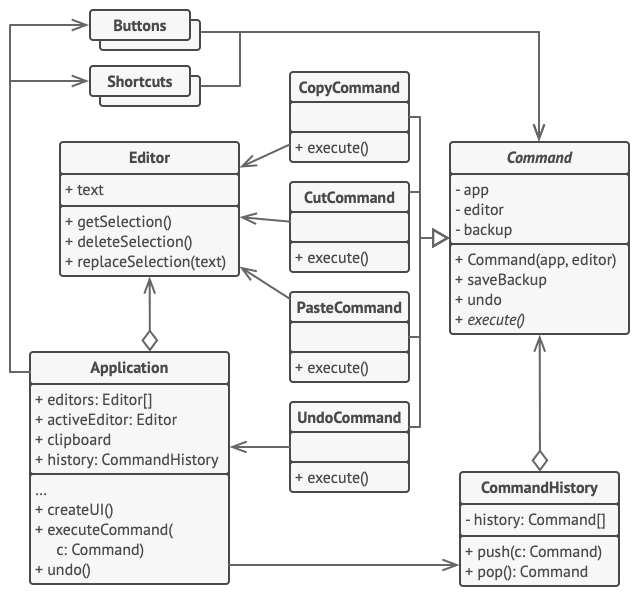
2. 行为模式 - 命令模式
亦称: 动作、事务、Action、Transaction、Command 意图 命令模式是一种行为设计模式, 它可将请求转换为一个包含与请求相关的所有信息的独立对象。 该转换让你能根据不同的请求将方法参数化、 延迟请求执行或将其放入队列中, 且能实现可撤销…...
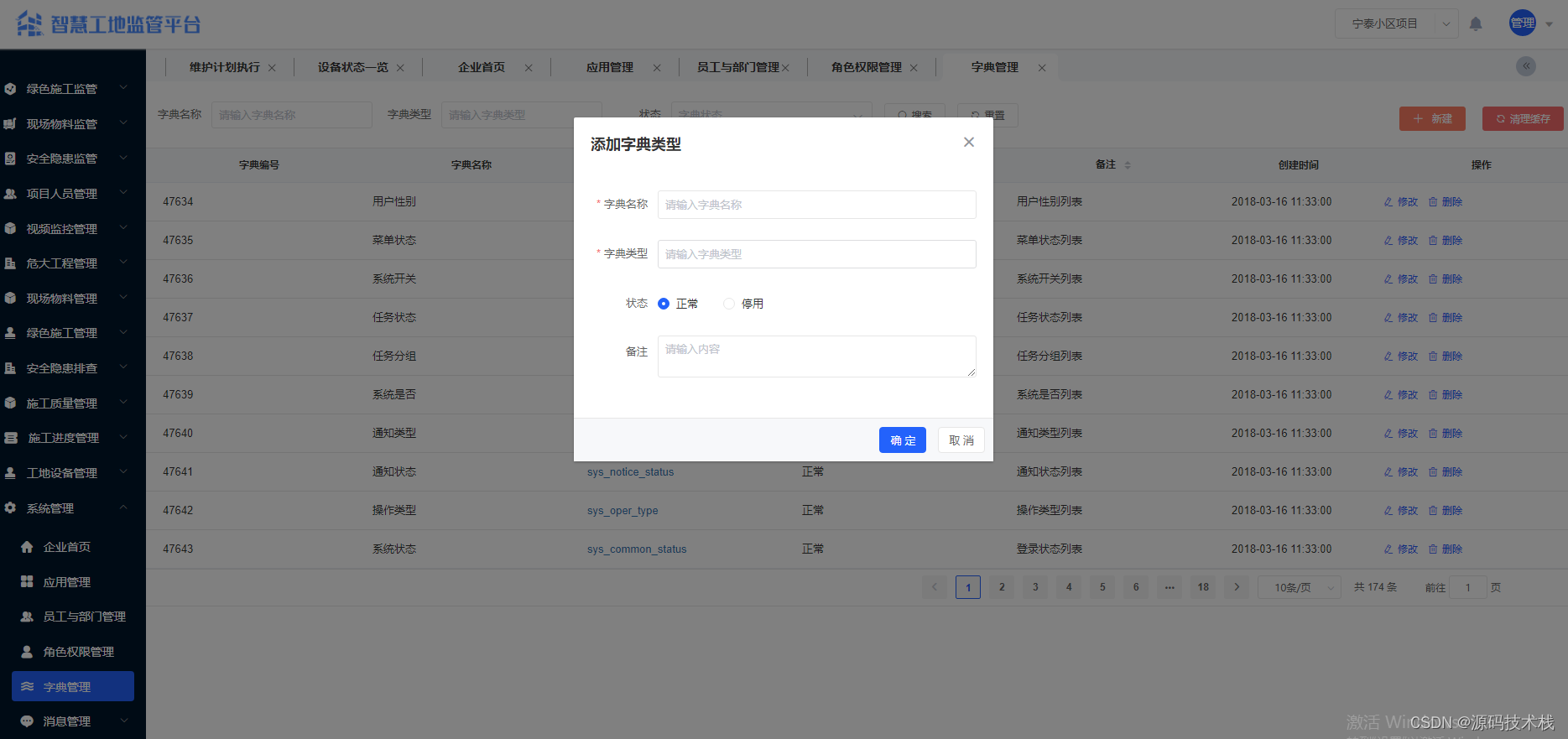
Java智慧工地源码 SAAS智慧工地源码 智慧工地管理可视化平台源码 带移动APP
一、系统主要功能介绍 系统功能介绍: 【项目人员管理】 1. 项目管理:项目名称、施工单位名称、项目地址、项目地址、总造价、总面积、施工准可证、开工日期、计划竣工日期、项目状态等。 2. 人员信息管理:支持身份证及人脸信息采集&#…...

php学习02-php标记风格
<?php echo "这是xml格式风格" ?><script language"php">echo 脚本风格标记 </script><% echo "这是asp格式风格" %>推荐使用xml格式风格 如果要使用简短风格和ASP风格,需要在php.ini中对其进行配置&#…...

13.1 jar文件
13.1 jar文件 java归档(JAR)文件,将应用程序打包后仅提供的单独文件,可包含类文件,也可包含图片、声音等其他类型文件。 JAR文件使用了大家熟悉的Zip压缩格式,pack200为通常的zip压缩算法,对类…...

论文阅读:Long-Term Visual Simultaneous Localization and Mapping
论文摘要指出,为了在长期变化的环境中准确进行定位,提出了一种新型的长期视觉SLAM(同步定位与地图构建)系统,该系统具备地图预测和动态物体移除功能。系统首先设计了一个高效的视觉点云匹配算法,将2D像素信…...
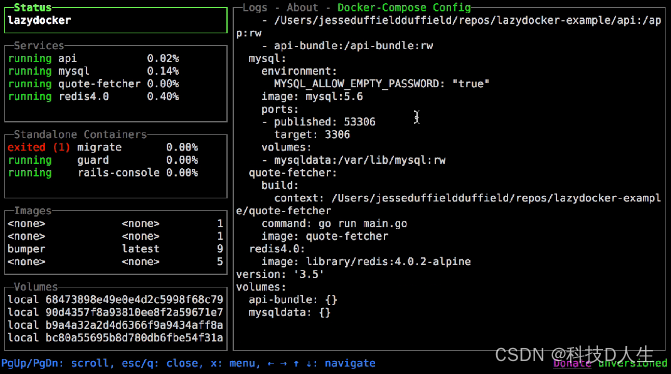
Docker 学习总结(80)—— 轻松驾驭容器,玩转 LazyDocker
前言 LazyDocker 是一个用户友好的命令行工具,简化了 Docker 的管理。它能够通过单一命令执行常见的 Docker 任务,如启动、停止、重启和移除容器。LazyDocker 还能轻松查看日志、清理未使用的容器和镜像,并自定义指标。 简绍 LazyDocker 是一个用户友好的 CLI 工具,可以轻…...
- MediaCodecList)
Android 13 - Media框架(24)- MediaCodecList
这一节我们要了解 MediaCodecList 中的信息是如何加载的,以及这些信息是如何使用到的。 // static sp<IMediaCodecList> MediaCodecList::getLocalInstance() {Mutex::Autolock autoLock(sInitMutex);if (sCodecList nullptr) {MediaCodecList *codecList n…...

【稳定检索|投稿优惠】2024年交通运输与能源动力国际学术会议(IACTEP 2024)
2024年交通运输与能源动力国际学术会议(IACTEP 2024) 2024 International Academic Conference on Transportation and Energy Power(IACTEP) 一、【会议简介】 2024年交通运输与能源动力国际学术会议(IACTEP 2024)将在美丽的三亚盛大启幕。本次会议将聚焦交通运输与能源动力等…...
React学习计划-React16--React基础(三)收集表单数据、高阶函数柯里化、类的复习
1. 收集表单数据 包含表单的组件分类 受控组件——页面中所有输入类的DOM,随着输入,把值存维护在状态里,需要用的时候去状态里取值(推荐,避免了过渡使用ref)非受控组件——页面中所有输入类的DOM,现用现取…...

研究生课程 |《数值分析》复习
搭配往年真题册食用最佳。...

55 回溯算法解黄金矿工问题
问题描述:你要开发一座金矿,地质学家已经探明了这座金矿中的资源分布,并用大小为m*n的网格grid进行了标注,每个单元格中的整数就表示这一单元格中的黄金数量;如果单元格是空的,那么就是0,为了使…...
[笔记]ByteBuffer垃圾回收
参考:https://blog.csdn.net/lom9357bye/article/details/133702169 public static void main(String[] args) throws Throwable {List<Object> list new ArrayList<>();Thread thread new Thread(() -> {ByteBuffer byteBuffer ByteBuffer.alloc…...

c++ opencv中unsigned char *、Mat、Qimage互相转换
unsigned char * 转Mat unsinged char * data img.data; Mat mat (h,w,cv_8UC3,data,0);void * 转Qimage uchar * bit (uchar*)pRknnInputData; QImage image QImage(bit, 2048,1536, QImage::Format_RGB888);qimage转Mat QImage image QImage (MODEL_INPUT_WIDTH_SIZE,MODE…...
法线贴图实现衣服上皱褶特效
在线工具推荐: 3D数字孪生场景编辑器 - GLTF/GLB材质纹理编辑器 - 3D模型在线转换 - Three.js AI自动纹理开发包 - YOLO 虚幻合成数据生成器 - 三维模型预览图生成器 - 3D模型语义搜索引擎 法线贴图在3D建模中扮演着重要的角色,它通过模拟表面的微…...

2017年第六届数学建模国际赛小美赛B题电子邮件中的笔迹分析解题全过程文档及程序
2017年第六届数学建模国际赛小美赛 B题 电子邮件中的笔迹分析 原题再现: 笔迹分析是一种非常特殊的调查形式,用于将人们与书面证据联系起来。在法庭或刑事调查中,通常要求笔迹鉴定人确认笔迹样本是否来自特定的人。由于许多语言证据出现在电…...

CentOS安装Python解释,CentOS设置python虚拟环境,linux设置python虚拟环境
一、安装python解释器 1、创建解释器安装的目录:/usr/local/python39 cd /usr/local mkdir python39 2、下载依赖 yum -y install zlib-devel bzip2-devel openssl-devel ncurses-devel sqlite-devel readline-devel tk-devel gcc make libffi-devel xz-devel …...
在线智能防雷监控(检测)系统应用方案
在线智能防雷监控系统是一种利用现代信息技术,对防雷设施的运行状态进行实时监测、管理和控制的系统,它可以有效提高防雷保护的安全性、可靠性和智能化程度,降低运维成本和风险,为用户提供全方位的防雷解决方案。 在线智能防雷监控…...
flutter + firebase 云消息通知教程 (android-安卓、ios-苹果)
如果能看到这篇文章的 一定已经对手机端的 消息推送通知 有了一定了解。 国内安卓厂商这里不提都有自己的FCM 可自行查找。(国内因无法科学原因 ,不能使用谷歌服务)只说海外的。 目前 adnroid 和 ios 推送消息分别叫 FCM 和 APNs。这里通过…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...
