初级数据结构(七)——二叉树
| 文中代码源文件已上传:数据结构源码 <-上一篇 初级数据结构(六)——堆 | NULL 下一篇-> |
1、写在前面
二叉树的基本概念在《初级数据结构(五)——树和二叉树的概念》中已经介绍得足够详细了。上一篇也演示了利用顺序表模拟二叉树。但链表形式的二叉树在逻辑上相对于顺序表尤其复杂,当然也比顺序表更为灵活。
链表形式的二叉树任何操作,本质都是有条件地遍历各个节点。而熟练掌握递归算法对遍历链表形式二叉树尤为重要。如果你对递归还犯迷糊可先翻阅《轻松搞懂递归算法》一文,其中对递归有较为详细的介绍。
2、建立
链表形式的二叉树的创建操作已经属于遍历操作了,本部分将通过边创建边说明的方式演示如何遍历二叉树。
2.1、前期工作
老样子,先建文件。

binaryTree.h :用于创建项目的结构体类型以及声明函数;
binaryTree.c :用于创建二叉树各种操作功能的函数;
main.c :仅创建 main 函数,用作测试。
这次演示是通过字符串创建二叉树,空节点以“ ? ”表示,所以在 binaryTree.h 中先写下如下代码:
#include <stdio.h>
#include <stdlib.h>typedef char DATATYPE;#define NULL_SYMBOL '?'
#define DATA_END '\0'
#define DATAPRT "%c"//创建二叉树节点
typedef struct Node
{DATATYPE data;struct Node* left;struct Node* right;
}Node;//函数声明-------------------------------------
//创建二叉树
extern Node* BinaryTreeCreate(DATATYPE*);
//销毁二叉树
extern void BinaryTreeDestroy(Node*);然后在 binaryTree.c 中 include 一下:
#include "binaryTree.h"在 main.c 中创建个 main 函数的空客:
#include "binaryTree.h"int main()
{return 0;
}2.2、常规遍历
二叉树有三种常用遍历顺序,称为前序、中序和后序。前中后序指的是访问节点中数据的次序。
前序:先访问根节点,之后问左树,最后访问右树。
中序:先访问左树,之后问根节点,最后访问右树。
后序:先访问左树,之后问右树,最后访问根节点。
先看图:

用前序访问上图第一棵树顺序是 A→B→C ,中序是 B→A→C ,后序则是 B→C→A 。而这是相对于子树而言的。如果访问上图第二棵树需要将树根据当前访问的节点拆分为子树。如用前序访问,先访问 D ,之后定位到 D 的左节子点 E , 但此时是先将 E 节点当作子树,访问的是该子树的根节点。 之后访问 G 也是如此。用前序访问的顺序是 D→E→G→F→H→I 。而实际访问顺序如下图:

D→E→G→NULL→NULL→NULL→F→H→NULL→NULL→I→NULL→NULL 。
用前序来说明可能不太明显。如果用中序,先定位到 D 节点,此时先不访问 D 的数据,而是访问 D 的左子节点 E 。而 E 作为子树,它还存在自己的左子节点,因此也不访问 E 的数据,而是它的子节点 G 。此时以 G 为根节点的子树不存在左子节点,因此访问 G 的数据,然后访问 G 的右子节点。但 G 不存在右子节点,所以访问完 G 的数据也就是访问完以 G 为根节点的子树,相当于 E 的左树访问完毕,此时才访问 E 的数据。下一步访问 E 的右子节点,但 E 不存在右子节点,所以 以 E 为根的子树访问完成,相当于 D 的左子树访问完毕,所以访问 D 的数据,然后访问 D 的右子树 F ……因此,以中序访问这棵树顺序是 G→E→D→H→F→I 。实际访问顺序:
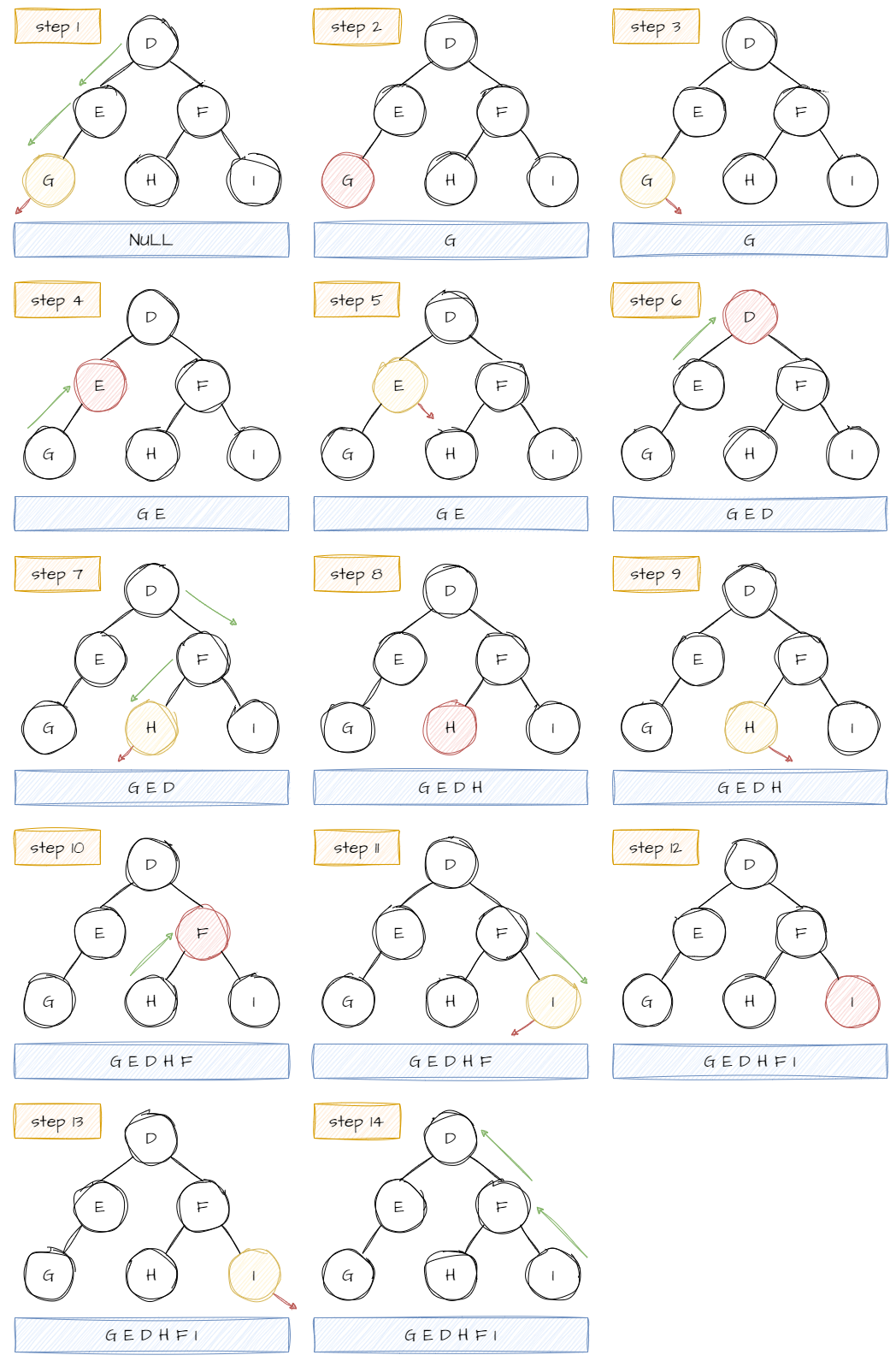
NULL→G→NULL→E→NULL→D→H→NULL→NULL→F→I→NULL→NULL 。
后序的逻辑可以类比中序,访问顺序是 G→E→H→I→F→D 。实际访问顺序:

NULL→NULL→G→NULL→E→NULL→NULL→H→NULL→NULL→I→F→D 。
2.3、操作函数
2.3.1、创建二叉树
创建二叉树的过程也是在遍历二叉树。而创建过程中,必须先有根节点,才能创建子树,所以建立二叉树是以前序边创建边访问建立的。
需要解决的问题是在创建节点的结构体时,并没有创建指向父节点的指针成员变量。当创建完左树之后,要如何回到根节点。这里先往回思考,在前中后序的说明中不难看出,这就是一种递归。树拆成子树,子树又拆成子树的子树……而不论拆分成哪一级子树,访问方式都是统一的顺序。而递归是具有回溯属性的,也就是说,用递归的方式创建二叉树再合适不过了。函数的代码便呼之欲出:
//创建二叉树
Node* BinaryTreeCreate(DATATYPE** ptr2_data)
{//参数有效性判定if (!ptr2_data || !*ptr2_data){fprintf(stderr, "Data Address NULL\n");return NULL;}//数据为空节点符号或末位尾符号则返回if (**ptr2_data == NULL_SYMBOL || **ptr2_data == DATA_END){return NULL;}//创建节点Node* node = NULL;while (!node){node = (Node*)malloc(sizeof(Node));}//前序递归node->data = **ptr2_data;*ptr2_data += !(**ptr2_data == DATA_END);node->left = BinaryTreeCreate(ptr2_data);*ptr2_data += !(**ptr2_data == DATA_END);node->right = BinaryTreeCreate(ptr2_data);return node;
}在 main 函数中用以下代码进行测试:
DATATYPE data[] = "abc??d??f?g?h";
DATATYPE* ptr_data = data;
Node* root = BinaryTreeCreate(&ptr_data);树并不像线性表那么直观,检查测试结果时最好自己先画图,然后在监视窗口中检查。对于以上测试结果应当如下图:

调试起来,将调试窗口中逐层展开,对其中的信息对比上图。或者另外画图, 将两张图作对比进行检查。

结果正确。顺带写出前中后三种顺序访问二叉树的函数。这里为了方便观察遍历顺序,多加一个参数用于控制是否显示空节点。先在 binaryTree.h 中加个枚举类型以完善传参时代码的可读性:
enum NULL_VISIBLE
{HIDE_NULL, //空节点不可见 = 0SHOW_NULL //空节点可见 = 1
};然后加声明:
//前序访问二叉树
extern void PreOrderTraversal(Node*, int);
//中序访问二叉树
extern void InOrderTraversal(Node*, int);
//后序访问二叉树
extern void PostOrderTraversal(Node*, int);函数具体内容:
//前序访问二叉树
void PreOrderTraversal(Node* root, int NULLvisible)
{//空树返回if (!root){if (NULLvisible == SHOW_NULL){printf("NULL ");}return;}printf(DATAPRT" ", root->data);PreOrderTraversal(root->left, NULLvisible);PreOrderTraversal(root->right, NULLvisible);
}//中序访问二叉树
void InOrderTraversal(Node* root, int NULLvisible)
{//空树返回if (!root){if (NULLvisible == SHOW_NULL){printf("NULL ");}return;}InOrderTraversal(root->left, NULLvisible);printf(DATAPRT" ", root->data);InOrderTraversal(root->right, NULLvisible);
}//后序访问二叉树
void PostOrderTraversal(Node* root, int NULLvisible)
{//空树返回if (!root){if (NULLvisible == SHOW_NULL){printf("NULL ");}return;}PostOrderTraversal(root->left, NULLvisible);PostOrderTraversal(root->right, NULLvisible);printf(DATAPRT" ", root->data);
}这里可以观察到,所谓前中后序不过是调整了一下访问 root->data 语句的位置,其余完全一样。
然后开始测试。
int main()
{DATATYPE data[] = "abc??d??f?g?h";DATATYPE* ptr_data = data;Node* root = BinaryTreeCreate(&ptr_data);//前序:printf("前序 --------------------\n");PreOrderTraversal(root, SHOW_NULL);printf("\n");PreOrderTraversal(root, HIDE_NULL);printf("\n");//中序printf("中序 --------------------\n");InOrderTraversal(root, SHOW_NULL);printf("\n");InOrderTraversal(root, HIDE_NULL);printf("\n");//后序printf("后序 --------------------\n");PostOrderTraversal(root, SHOW_NULL);printf("\n");PostOrderTraversal(root, HIDE_NULL);printf("\n");return 0;
}
对比上面的图,说明代码正确。
2.3.2、销毁二叉树
销毁跟创建是同样的逻辑,必须从底层开始销毁。当然也可以从根部销毁,但如果不先销毁子节点,一旦销毁根节点之后便无法再找到子节点的地址,因此还得对子节点地址进行记录后再销毁,显得过于麻烦。因此采用后序遍历销毁最为简便。
//销毁二叉树
void BinaryTreeDestroy(Node* root)
{//空树直接返回if (!root) return;//后序递归销毁节点BinaryTreeDestroy(root->left);BinaryTreeDestroy(root->right);free(root);
}这个函数测试过程需要一步一步调试观察。 实际上跟之前后序访问的函数是一个道理,这里也没必要再多作测试。但使用完该函数记得把根节点指针置空。
2.3.3、搜索
搜索也是通过遍历比对节点中的数据,再返回节点地址。
必不可少的声明:
//二叉树搜索
extern Node* BinaryTreeSearch(Node*, DATATYPE);代码:
//二叉树搜索
Node* BinaryTreeSearch(Node* root, DATATYPE data)
{//空树直接返回if (!root) return NULL;//创建节点地址指针Node* node = NULL;//前序搜索node = (root->data == data ? root : NULL);node = (node ? node : BinaryTreeSearch(root->left, data));node = (node ? node : BinaryTreeSearch(root->right, data));return node;
}在刚才创建的二叉树基础上测试:
Node* node = NULL;node = BinaryTreeSearch(root, 'f');if (node)printf("Found Data '"DATAPRT"' In 0x%p\n", node->data, node);elseprintf("Not Found\n");node = BinaryTreeSearch(root, 'j');if (node)printf("Found Data '"DATAPRT"' In %p\n", node->data, node);elseprintf("Not Found\n");
测试通过。此外,搜索既然实现了,修改就不必说了,这里不再演示。
3、层序
除了之前提到的前中后序遍历二叉树以外,还有层序遍历。顾名思义,就是逐层遍历二叉树中每个节点。层序遍历是最复杂的一种遍历方式。由于二叉树节点中并不包含兄弟节点和堂兄弟节点的指针,因此层序遍历需要其他变量来记录各层节点的左右子节点,并按照一定顺序排序。
3.1、队列
这里可以利用队列的特性,访问完根节点后,对左右子节点地址进行入队,并将根节点出队,从而实现遍历。因此,这里先在 binaryTree.h 中创建个队列。
//队列类型
typedef struct Queue
{int top;int bottom;size_t capacity;Node* data[];
}Queue;之后是在 binaryTree.c 中创建操作队列的各个函数。
//创建队列并初始化
static Queue* QueueCreate()
{Queue* queue = NULL;//创建队列while (!queue){queue = (Queue*)malloc(sizeof(Queue) + sizeof(Node*) * 4);}queue->top = -1;queue->bottom = -1;queue->capacity = 4;//返回队列return queue;
}//数据入队
static void QueuePush(Queue** queue, Node* node)
{//若队列空间不足,扩容if ((*queue)->top + 1 >= (*queue)->capacity){Queue* tempQueue = NULL;while (!tempQueue){tempQueue = (Queue*)realloc(*queue, sizeof(Queue) + sizeof(Node*) * (*queue)->capacity * 2);}(*queue) = tempQueue;(*queue)->capacity *= 2;}//节点入队(*queue)->bottom = ((*queue)->bottom == -1 ? 0 : (*queue)->bottom);(*queue)->top++;(*queue)->data[(*queue)->top] = node;
}//数据出队
static void QueuePop(Queue* queue)
{//空队列返回if (queue->top == -1)return;//出队queue->bottom++;//出队后若为空队列if (queue->bottom > queue->top){queue->bottom = -1;queue->top = -1;}
}3.2、层序访问
由于二叉树是有序树,每一层节点从左到右必然是有序的。仍以这棵树作演示:

首先将根节点 D 入队,访问完根节点后,将左右子节点 E、F 依次入队,排在 D 之后,然后弹出 D 。之后访问 E,再将 E 的左右子节点 G 和 NULL 入队,弹出 E 。继续访问 F ,H、I 入队后再弹出 F 。如果当前根节点为 NULL ,则不再将子节点入队,仅仅弹出 NULL 。最后当队列为空时,树也遍历完毕。
根据以上描述,可以知道层序访问顺序为 D→E→F→G→H→I,实际访问顺序:

D→E→F→G→NULL→H→I→NULL→NULL→NULL→NULL→NULL→NULL 。
3.3、代码部分
思路已经有了,代码也就顺理成章了。
//层序打印
static void LevelOrderPrint(Queue** queue)
{//空队列返回if ((*queue)->top == -1) return;//非空节点的左右子节点入队if ((*queue)->data[(*queue)->bottom]){QueuePush(queue, ((*queue)->data[(*queue)->bottom])->left);QueuePush(queue, ((*queue)->data[(*queue)->bottom])->right);}//打印非空节点if ((*queue)->data[(*queue)->bottom] != NULL){printf(DATAPRT" ", ((*queue)->data[(*queue)->bottom])->data);}//根节点出队QueuePop(*queue);LevelOrderPrint(queue);
}//层序遍历二叉树
void LevelOrderTraversal(Node* root)
{//创建队列Queue* queue = QueueCreate();//根节点入队QueuePush(&queue, root);//层序打印LevelOrderPrint(&queue);//销毁队列free(queue);
}仍沿用开头的测试案例,然后在 main 函数最后加入以下语句进行测试:
//层序printf("层序 --------------------\n");LevelOrderTraversal(root);printf("\n");![]()
至此完成。
相关文章:

初级数据结构(七)——二叉树
文中代码源文件已上传:数据结构源码 <-上一篇 初级数据结构(六)——堆 | NULL 下一篇-> 1、写在前面 二叉树的基本概念在《初级数据结构(五)——树和二叉树的概念》中已经介绍得足够详细了。上一…...

对比学习综述
1.简介 2.相关工作 2.1、Inst Disc 代理任务:个体判别。把每一个图片看作是一种类别,把每一个图片都区分开来。 正负样本选择:正样本是图片本身,负样本是数据集里的其他图片,该文章从memory bank中随机抽取4096个负…...

R语言【cli】——cli_warn可以更便捷的在控制台输出警告信息
Package cli version 3.6.2 cli_warn(message, ..., .envir parent.frame()) 参数【message】:它是通过调用 cli_bullets() 进行格式化的。进一步地,还需要调用 inline-makeup(内联标记)。 参数【...】:传递给 rlan…...
从零开始创建GPTs 人人都可以编写自己的ChatGPT产品
在这个人工智能迅猛发展的时代,GPT(生成式预训练变换器)已经成为一项令人兴奋的技术,它打开了创意和知识的新大门。无论你是一名编程新手、一位热爱探索的学生,还是对未来充满好奇的专业人士,GPTs都可以为你…...

人工智能对网络安全的影响
技术的快速发展带来了不断增长的威胁环境,网络犯罪分子和恶意行为者利用我们互联世界中的漏洞。在这个数字时代,数据泄露和网络攻击呈上升趋势,仅靠传统的安全措施已经不够了。人工智能 (AI) 的进步彻底改变了网络安全…...

鸿蒙(HarmonyOS)项目方舟框架(ArkUI)之TextInput输入框组件
鸿蒙(HarmonyOS)项目方舟框架(ArkUI)之TextInput输入框组件 一、操作环境 操作系统: Windows 10 专业版 IDE:DevEco Studio 3.1 SDK:HarmonyOS 3.1 二、TextInput 接口 TextInput(value?:{placeholder?: ResourceStr, tex…...

【C++入门到精通】互斥锁 (Mutex) C++11 [ C++入门 ]
阅读导航 引言一、Mutex的简介二、Mutex的种类1. std::mutex (基本互斥锁)2. std::recursive_mutex (递归互斥锁)3. std::timed_mutex (限时等待互斥锁)4. std::recursive_timed_mutex (限时等待…...
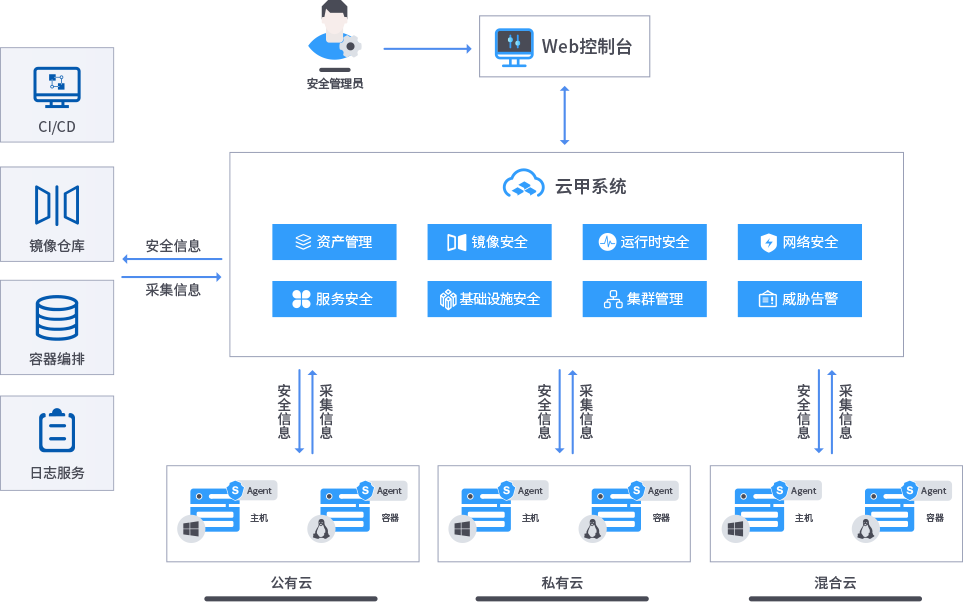
安全狗云原生安全-云甲·云原生容器安全管理系统
随着云计算的快速发展,容器技术逐渐成为主流。然而,随着容器的普及,安全问题也日益突出。为了解决这一问题,安全狗推出了云原生容器安全管理系统——云甲。 云甲是安全狗云原生安全的重要组成部分,它采用了先进的云原生…...

Python 学习路线:介绍、基础语法、数据结构、算法、高级主题、框架及异步编程详解
Python 介绍 Python 是一种 高级 的、解释型 的、通用 的编程语言。其设计哲学强调代码的可读性,使用显著的缩进。Python 是 动态类型 和 垃圾收集 的。 基本语法 设置 Python 环境并开始基础知识。 文章链接:Python 安装与快速入门 变量 变量用于…...
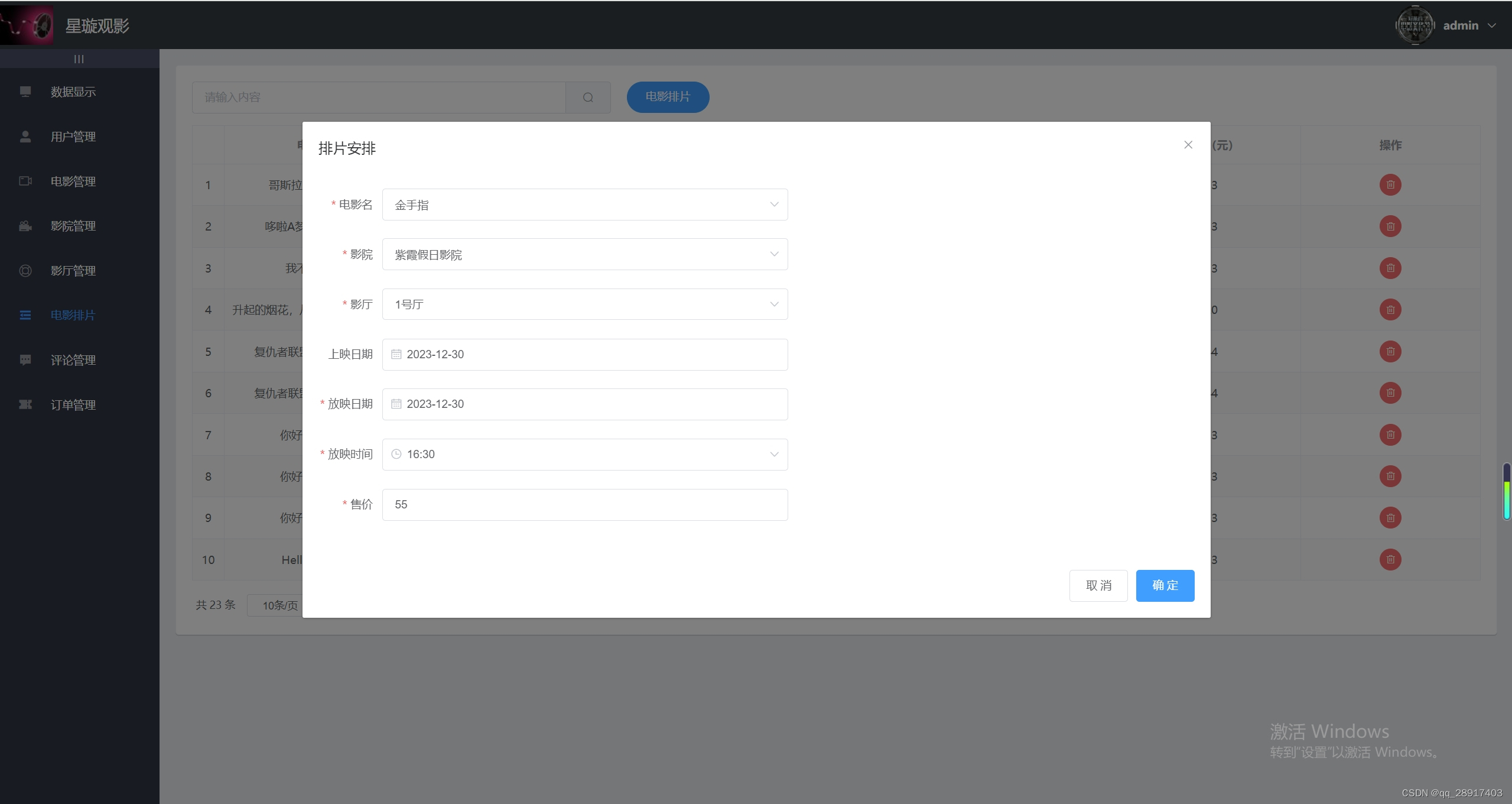
基于Java+SpringBoot+Mybaties-plus+Vue+ElementUI+Vant 电影院订票管理系统 的设计与实现
一.项目介绍 基于SpringBootVue 电影院订票管理系统 分为前端和后端。 前端(用户): 登录后支持查看首页、电影、影院和我的信息 支持查看正在热映和即将上映的电影信息 支持购票(需选择影院座位)、看过(评论…...
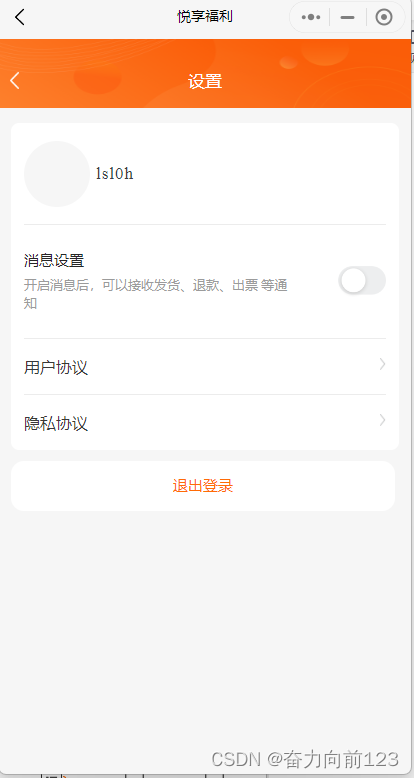
轻量级购物小程序H5产品设计经典样例
主要是看到这个产品设计的不错值得借鉴特记录如下: 不过大多数购物app都大致相同,这个算是经典样例,几乎都可以复制,我第一次使用,感觉和顺畅。看上去产品是经过打磨的,布局非常好。内容也很丰富。支持异业…...

final, finally, finalize 的区别?
1.final 用于声明属性,方法和类,分别表示属性不可变,方法不可覆盖,类不可继承。 内部类要访问局部变量,局部变量必须定义成 final 类型 2.finally 是异常处理语句结构的一部分,表示总是执行 3.finalize …...

4.使用 Blazor 构建 Web 应用程序
微软官方培训 了解如何通过 Blazor Web 用户界面框架构建你的第一个 Web 应用程序。 https://learn.microsoft.com/zh-cn/training/paths/build-web-apps-with-blazor/?viewaspnetcore-8.0 8个模块 目录 微软官方培训 1.使用 Blazor 进行 Web 开发的简介 2.使用 Blazor…...
CentOS操作学习(二)
上一篇学习了CentOS的常用指令CentOS指令学习-CSDN博客 现在我们接着学习 一、Vi编辑器 这是CentOS中自带的编辑器 三种模式 进入编辑模式后 i:在光标所在字符前开始插入a:在光标所在字符串后开始插入o:在光标所在行的下面另起一新行插入…...

OpenCV技术应用(9)— 视频的暂停播放和继续播放
前言:Hello大家好,我是小哥谈。本节课就手把手教大家如何控制视频的暂停播放和继续播放,希望大家学习之后能够有所收获~!🌈 目录 🚀1.技术介绍 🚀2.实现代码 🚀1.技术介绍…...

C#时间戳转换
时间戳转化为时间 long oldtime1703235741; System.DateTime startTime TimeZone.CurrentTimeZone.ToLocalTime(new System.DateTime(1970, 1, 1, 0, 0, 0, 0)); var newtimestartTime.AddMilliseconds(oldtime).ToString("yyyy-MM-dd HH:mm:ss.fff"); 时间转化为时…...
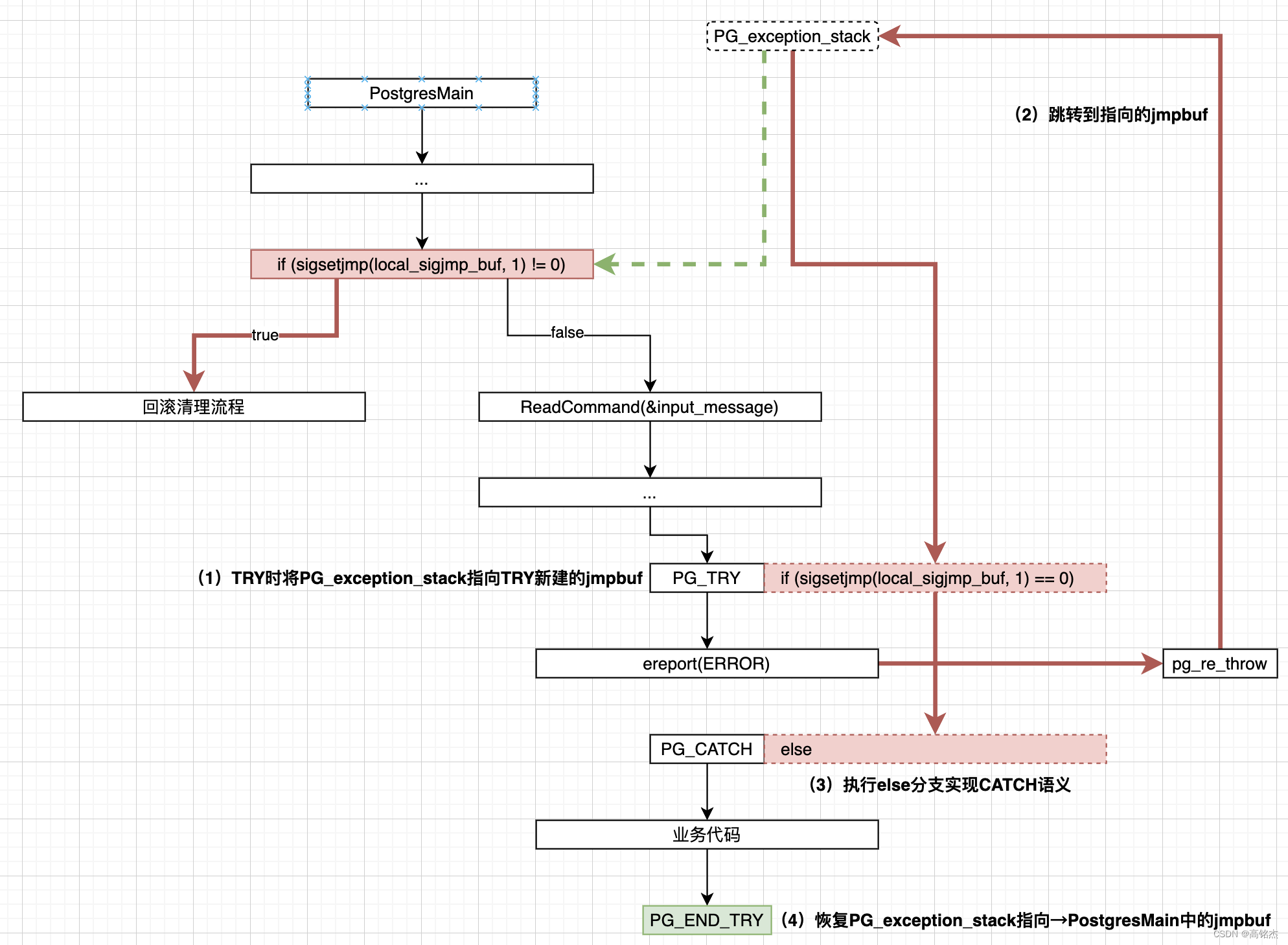
Postgresql源码(118)elog/ereport报错跳转功能分析
1 日志接口 elog.c完成PG中日志的生产、记录工作,对外常用接口如下: 1.1 最常用的ereport和elog ereport(ERROR,(errcode(ERRCODE_UNDEFINED_TABLE),errmsg("relation \"%s\" does not exist",relation->relname)));elog(ERRO…...

Python Selenium中的强大等待设置详解
更多资料获取 📚 个人网站:ipengtao.com 在Web自动化测试中,等待是至关重要的一环,而Selenium提供了丰富的等待设置来确保测试脚本的可靠性和稳定性。本文将深入研究Python Selenium中常用的必备等待设置,包括显式等待…...
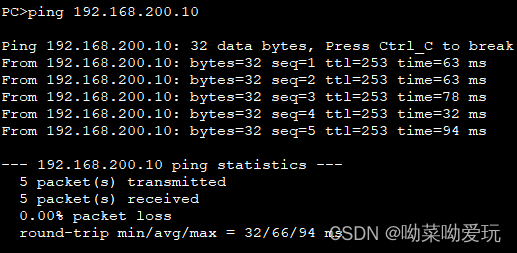
ACL实现固定时间访问资源——项目
文章目录 一、前言二、项目拓扑三、项目需求四、配置思路五、配置步骤1 IP地址2 端口类型3 静态路由4 流策略 六、结语 免责声明 本文旨在提供信息和解决问题的建议,观点和建议可能不适用于个人情况,仅供参考!!! 文章中…...

前端学习——关于前端框架的思考
前端框架 我们知道在AngularJS,react,vue等前端框架出现之前,前端开发都是通过js直接操作dom树来实现的,而有了前端框架之后,前端开发基本上不需要在直接操作dom树,相当于在原生html的dom树之间和前端程序…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...
