Codeforces Round 916 (Div. 3)(E:贪心 F贪心dfs G tarjan+topsort +线段树优化建图)
A:直接暴力统计每个字符的次数是否达标即可
#include<bits/stdc++.h>
using namespace std;
const int N = 3e5+10,mod=998244353;
#define int long long
typedef long long LL;
typedef pair<int, int> PII;
typedef unsigned long long ULL;const long long inf=1e17;
using node=tuple<int,int,int,int>;
int n,m,k;
int a[N];void solve()
{cin>>n;string s;cin>>s;map<int,int> mp;for(auto x:s)mp[x-'A'+1]++;int res=0;for(int i=1;i<=n;i++){if(mp[i]>=i) res++;}cout<<res<<"\n";
}signed main()
{cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int t=1;cin>>t;while(t--) solve();
}B:直接先输出所需要的k,然后降序输出剩下的即可
#include<bits/stdc++.h>
using namespace std;
const int N = 3e5+10,mod=998244353;
#define int long long
typedef long long LL;
typedef pair<int, int> PII;
typedef unsigned long long ULL;const long long inf=1e17;
using node=tuple<int,int,int,int>;
int n,m,k;
int a[N],b[N];
PII d[N];
void solve()
{cin>>n>>k;int l=1,r=n;for(int i=n-k;i<=n;i++){cout<<i<<" ";}for(int i=n-k-1;i>=1;i--) cout<<i<<" ";cout<<"\n";
}signed main()
{cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int t=1;cin>>t;while(t--) solve();
}C:
直接枚举最后操作到哪个位置就行了,然后贪心一直操作1到i的位置的b最大值即可
#include<bits/stdc++.h>
using namespace std;
const int N = 3e5+10,mod=998244353;
#define int long long
typedef long long LL;
typedef pair<int, int> PII;
typedef unsigned long long ULL;const long long inf=1e17;
using node=tuple<int,int,int,int>;
int n,m,k;
int a[N],b[N];void solve()
{cin>>n>>k;vector<int> s(n+10);for(int i=1;i<=n;i++) cin>>a[i];for(int i=1;i<=n;i++)cin>>b[i];int mx=0;int res=0,now=0;for(int i=1;i<=n;i++){if(i>k) break;now+=a[i];mx=max(mx,b[i]);res=max(res,now+mx*(k-i));}cout<<res<<"\n";
}signed main()
{cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int t=1;cin>>t;while(t--) solve();
}D:
先固定第一次是A 第二次是B 第三次是C
枚举B为中介点i,然后求1到i-1的A的最大值,和i+1到n的C最大值即可
然后三个数有6个排列暴力枚举即可
#include<bits/stdc++.h>
using namespace std;
const int N = 3e5+10,mod=998244353;
#define int long long
typedef long long LL;
typedef pair<int, int> PII;
typedef unsigned long long ULL;const long long inf=1e17;
using node=tuple<int,int,int,int>;
int n,m,k;
int a[N],b[N];void solve()
{cin>>n;vector<int> a(n+10),b(n+10),c(n+10);for(int i=1;i<=n;i++) cin>>a[i];for(int i=1;i<=n;i++) cin>>b[i];for(int i=1;i<=n;i++) cin>>c[i];auto get=[&](vector<int>&a,vector<int>&b,vector<int>&c){int mx=0;vector<int> l(n+10),r(n+10);for(int i=1;i<=n;i++) l[i]=max(a[i],l[i-1]);for(int i=n;i>=1;i--) r[i]=max(r[i+1],c[i]);for(int i=2;i<n;i++){mx=max(mx,l[i-1]+r[i+1]+b[i]);}return mx;};cout<<max({get(a,b,c),get(a,c,b),get(b,a,c),get(b,c,a),get(c,a,b),get(c,b,a)})<<"\n";
}signed main()
{cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int t=1;cin>>t;while(t--) solve();
}E:这个题我好像杭电多校做过...
范围那么大不太可能dp,不如从贪心切入
先想某个人取i位置贡献是啥,贡献是这个人获得了(a[i]-1),另外一个人失去了b[i]
所以这个人其实一共获得了a[i]-1+b[i]的价值
所以我们直接拿个堆维护当前a[i]+b[i]的最大值即可
#include<bits/stdc++.h>
using namespace std;
const int N = 3e5+10,mod=998244353;
#define int long long
typedef long long LL;
typedef pair<int, int> PII;
typedef unsigned long long ULL;const long long inf=1e17;
using node=tuple<int,int,int,int>;
int n,m,k;
int a[N],b[N];
PII d[N];
void solve()
{cin>>n;for(int i=1;i<=n;i++) cin>>a[i];for(int i=1;i<=n;i++) cin>>b[i];vector<bool> st(n+10);priority_queue<PII> q;for(int i=1;i<=n;i++){q.emplace(a[i]+b[i],i);}//sort(d+1,d+1+n);int res=0;int now=0;int l=1,r=n;for(int i=1;i<=n;i++,now^=1){if(now==0){auto x=q.top();res+=a[x.second]-1;q.pop();}else{auto x=q.top();res-=(b[x.second]-1);q.pop();}}cout<<res<<"\n";
}signed main()
{cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int t=1;cin>>t;while(t--) solve();
}F:
贪心吧我觉得
手玩一下样例可以发现,这跟子树大小有关的
假如1的子树有三个
x,y,z,他们不能内部消化的点分别是是 4 2 1
x,y,z,他们本身的子树大小是 4 6 4
我们的目标是让内部不能消化的点通过匹配其他点来消失
我们可以发现x的4个不能内部消化的点,可以和y和z一共3个不能消化的点配对
那么是不是就多出了一个不能消化点呢?
答案是错误的,不妨这么想,x的四个点直接和y子树的随便四个点来配合,
y的两个不能内部消化的点和z可以内部消化的点和不能内部消化的点都能拿来随便用。
可是如果x的子树不能配对的子树大小是10,那么这10个子树不能通过y,z的子树的点来全部配对完
肯定还有剩余的,且这些剩余的不能内部消化
贪心的假设当前点u的儿子节点x不能配对的数最大是 mx,那么如果,他其他子树的全部节点都不够这个mx大,即拿其他子树的全部节点都不能匹配完当前最大子树不能内部消化的点数,那么
他剩下既不能跟其他子树匹配且不能内部消化的剩余的点mx-(sz[u]-size[x])的往上传,让父节点的其他节点来匹配
所以我们维护一个当前u点不能配对的数 res.first
res.second就是维护的当前子树的大小
#include<iostream>
#include<vector>
#include<cassert>
using namespace std;
int N;
vector<int>G[2<<17];
int ch[2<<17];
int dfs0(int u)
{ch[u]=1;for(int v:G[u])ch[u]+=dfs0(v);return ch[u];
}
int dfs1(int u,int L)
{int mx=0,mxv=-1;for(int v:G[u]){if(mx<ch[v])mx=ch[v],mxv=v;}if(ch[u]-1-mx>=mx){return min(L,(ch[u]-1)/2*2);}else{assert(mxv!=-1);int nL=mx-(ch[u]-1-mx);int ret=dfs1(mxv,nL);ret+=(ch[u]-1-mx)*2;return min(L,ret);}
}
int main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int T;cin>>T;for(;T--;){cin>>N;for(int i=0;i<N;i++)G[i].clear();for(int i=1;i<N;i++){int p;cin>>p;G[p-1].push_back(i);}dfs0(0);cout<<dfs1(0,N)/2<<"\n";}
}
G1:
操作题先想操作的性质
比如例子
3 2 1 3 1 2
我们操作2,那么两个2之间就能全部点亮,再通过3再点亮第一个3
即我们颜色为2的点,可以点亮3 1的点,再通过3 1的点再点亮其他
假设最坏情况下,可以一直点亮是什么情况呢
是整个区间都变成一个环
为什么呢
比如 1 2 1 2
点1可以到点2
点2可以到点1,构成环
如果是1 2 2 1
1可以到点2,但是点2不能到1
把环缩成点后就变成了经典的拓扑排序问题
第一个答案就是这个拓扑排序入度为0的点,
方案数就是入度为0的点之间的大小相乘即可
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5+10,mod=998244353;
#define int long long
typedef long long LL;
typedef pair<int, int> PII;
typedef unsigned long long ULL;const long long inf=1e17;
using node=tuple<int,int,int,int>;
int n,m,k;
int a[N],b[N];
vector<int> g[N];int dfn[N],low[N];
int scc_cnt,timestamp;
int stk[N],id[N];
bool in_stk[N];
int sz[N],in[N];
int top;
void tarjan(int u){dfn[u] = low[u] = ++ timestamp;stk[ ++ top] = u, in_stk[u] = true;for (auto j:g[u]){if (!dfn[j]){tarjan(j);low[u] = min(low[u], low[j]);}else if (in_stk[j]) low[u] = min(low[u], dfn[j]);}if (dfn[u] == low[u]){++ scc_cnt;int y;do {y = stk[top -- ];in_stk[y] = false;id[y] = scc_cnt;sz[scc_cnt]++;} while (y != u);}}
void solve()
{cin>>n; scc_cnt=timestamp=top=0;for(int i=1;i<=n;i++){g[i].clear();dfn[i]=low[i]=0;in_stk[i]=false;sz[i]=id[i]=in[i]=0;}vector<int> l(n*2+10),r(n*2+10);for(int i=1;i<=n*2;i++){cin>>a[i];if(l[a[i]]==0) l[a[i]]=i;else r[a[i]]=i;} vector<PII> E;for(int i=1;i<=n;i++){for(int j=l[i]+1;j<=r[i]-1;j++){g[i].push_back(a[j]);E.push_back({i,a[j]});}}for(int i=1;i<=n;i++) if(!dfn[i]) tarjan(i);for(auto [u,v]:E){if(id[u]==id[v]) continue;in[id[v]]++;}int ans=1,cnt=0;for(int i=1;i<=scc_cnt;i++){if(!in[i]){cnt++;ans=2ll*ans*sz[i]%mod;}}cout<<cnt<<" "<<ans<<"\n";
}signed main()
{cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int t=1;cin>>t;while(t--) solve();
}G2:
线段树优化建图,每个点最多有nlogn个出边
用线段树优化建图后
我前面有个博客写过tarjan缩点后
因为是拓扑序大的 scc_cnt小,因为tarjan是先到底部的,底部的点会先缩,再回溯到上面缩,
所以拓扑排序正常是从scc_cnt大入度小,所以从scc_cnt大的点开始拓扑排序回去即可
每个点再把他当前联通块的点标记,标记为入度不为0即可
#include<iostream>
#include<cstring>
#include<vector>
#include<array>
using namespace std;
using LL = long long;
const int maxn = 4e5 + 5, mod = 998244353;struct SCC{vector<vector<int> > g, scc;vector<int> dfn, low, stk, id;vector<bool> ins;int ts, n;SCC(const vector<vector<int> > &g) : g(g){n = (int)g.size();dfn.assign(n, 0);low.assign(n, 0);id.assign(n, -1);ins.assign(n, false);stk.reserve(n);ts = 0;build();}void tarjan(int u){dfn[u] = low[u] = ++ts;stk.push_back(u);ins[u] = 1;for(auto j : g[u]){if (!dfn[j]){tarjan(j);low[u] = min(low[u], low[j]);}else if (ins[j]) low[u] = min(low[u], dfn[j]);}if (dfn[u] == low[u]){int scc_cnt = scc.size();scc.push_back({});int y;do{y = stk.back();stk.pop_back();id[y] = scc_cnt;ins[y] = 0;scc.back().push_back(y);}while(y != u);}}void build(){for(int i = 0; i < n; i++){if (!dfn[i]){tarjan(i);}}}
};vector<vector<int> > g;
int a[maxn];
int n;int b[maxn];
void build(int u, int l, int r){if (l == r){g[u].push_back(8 * n + a[r]);g[8*n+a[r]].push_back(u);return;}int mid = (l + r) / 2;g[u].push_back(2 * u);g[u].push_back(2 * u + 1);build(2 * u, l, mid); build(2 * u + 1, mid + 1, r);
}void modify(int u, int l, int r, int L, int R, int x){if (l > R || r < L) return;if (l >= L && r <= R){g[x].push_back(u);return;}int mid = (l + r) / 2;modify(2 * u, l, mid, L, R, x);modify(2 * u + 1, mid + 1, r, L, R, x);
}int main(){cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int T;cin >> T;while(T--){cin >> n;vector<array<int, 2> > pos(n + 1);for(int i = 1; i <= 2 * n; i++){cin >> a[i];if (pos[a[i]][0] == 0){pos[a[i]][0] = i;}else{pos[a[i]][1] = i;}}g.assign(9 * n + 1, {});build(1, 1, 2 * n);for(int i = 1; i <= n; i++){auto [l, r] = pos[i];if (l + 1 <= r - 1){modify(1, 1, 2 * n, l + 1, r - 1, 8 * n + i);}}SCC scc(g);const int m = scc.scc.size();vector<int> c(m);for(int i = 0; i < m; i++){int s = 0;for(auto x : scc.scc[i]){s += (x > 8 * n);}c[i] = s;}int cnt = 0, sum = 1;vector<int> bad(m);for(int i = m - 1; i >= 0; i--){if (!bad[i] && c[i] > 0){cnt += 1;sum = 2LL * sum * c[i] % mod;}bad[i] |= (c[i] > 0);for(auto x : scc.scc[i]){for(auto j : g[x]){if (scc.id[j] != i){bad[scc.id[j]] |= bad[i];}}}}cout << cnt << ' ' << sum << '\n';}}不会线段树优化建图的看这篇文章
「算法笔记」线段树优化建图 - maoyiting - 博客园 (cnblogs.com)
相关文章:
(E:贪心 F贪心dfs G tarjan+topsort +线段树优化建图))
Codeforces Round 916 (Div. 3)(E:贪心 F贪心dfs G tarjan+topsort +线段树优化建图)
A:直接暴力统计每个字符的次数是否达标即可 #include<bits/stdc.h> using namespace std; const int N 3e510,mod998244353; #define int long long typedef long long LL; typedef pair<int, int> PII; typedef unsigned long long ULL;const long l…...
eNSP错误40,原因三:windows10自带虚拟化软件Hyper-V
问题描述 Hyper-V软件与VirtualBox不兼容,一旦开启Hyper-V的话eNSP的路由器就会无法开启,显示ERROR 40 原理 大家注意看hypervisor的两种类型: 左边的是开启hypervisor的Type-1,hypervisor在启用的时候,宿主机也相…...

Maven将Jar包打入本地仓库
Maven将Jar包打入本地仓库 Maven将Jar包打入本地仓库嘚吧嘚下载Maven配置Maven新建MAVEN_HOME编辑Path验证Maven配置 Jar包打入Maven仓库 Maven将Jar包打入本地仓库 嘚吧嘚 最近项目用到一个Jar包,不能从远程仓库拉取,只有一个Jar包,所以需…...
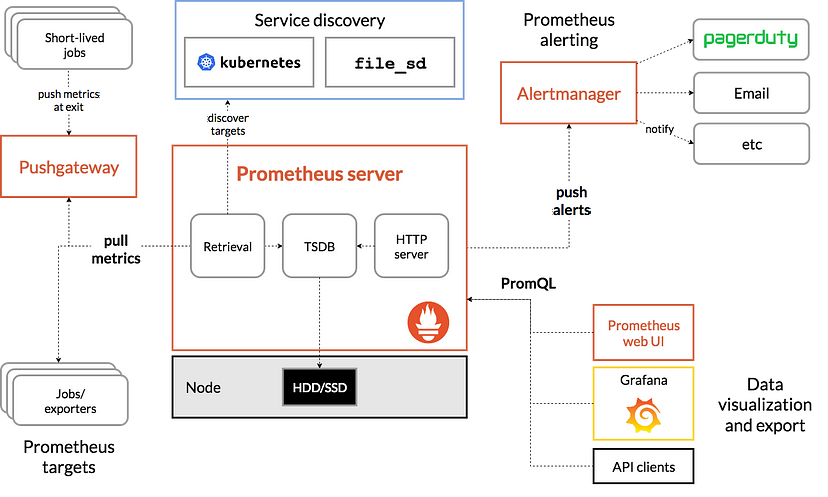
如何使用 Helm 在 K8s 上集成 Prometheus 和 Grafana|Part 1
本系列将分成三个部分,您将学习如何使用 Helm 在 Kubernetes 上集成 Prometheus 和 Grafana,以及如何在 Grafana 上创建一个简单的控制面板。Prometheus 和 Grafana 是 Kubernetes 最受欢迎的两种开源监控工具。学习如何使用 Helm 集成这两个工具&#x…...
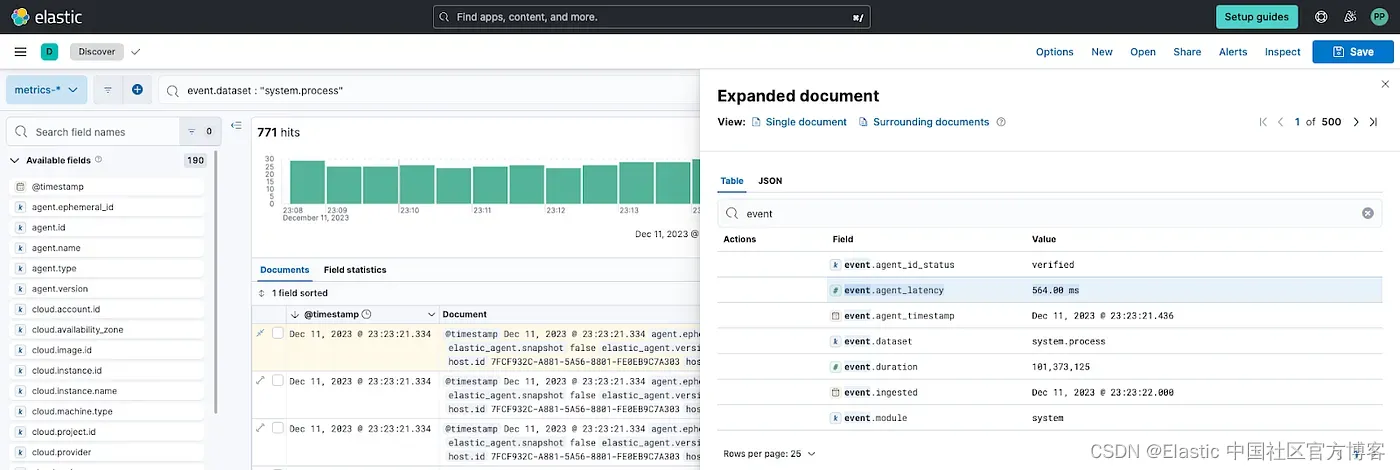
Observability:捕获 Elastic Agent 和 Elasticsearch 之间的延迟
在现代 IT 基础设施的动态环境中,高效的数据收集和分析至关重要。 Elastic Agent 是 Elastic Stack 的关键组件,通过促进将数据无缝摄取到 Elasticsearch 中,在此过程中发挥着至关重要的作用。 然而,显着影响此过程整体有效性的关…...

Ubuntu 常用命令之 less 命令用法介绍
📑Linux/Ubuntu 常用命令归类整理 less命令是一个在Unix和Unix-like系统中用于查看文件内容的命令行工具。与more命令相比,less命令提供了更多的功能和灵活性,例如向前和向后滚动查看文件,搜索文本,查看长行等。 les…...

探索Node.js包管理器npm:介绍与使用指南
引言: 在现代软件开发中,包管理器已经成为了不可或缺的工具。它们简化了软件的安装、升级和管理过程,使得开发者能够更加高效地构建项目。而作为Node.js的官方包管理器,npm(Node Package Manager)无疑是最受…...

探讨APP自动化测试工具的重要性
随着移动应用市场的蓬勃发展,企业对于保证其移动应用质量和用户体验的需求日益迫切。在这一背景下,APP自动化测试工具正变得越来越重要,成为企业成功的关键组成部分。本文将探讨APP自动化测试工具对企业的重要性,并为您解析其在提…...
)
el-date-picker日期时间插件只允许选择年月日小时并做可选择范围限制(精确到小时的范围)
一、首先明确下这个需求 1、要求只能选择年月日时,不要分钟和秒 2、根据后台返回的开始时间和天数设置可选择的开始时间和结束时间范围(包含小时)比如后台返回的开始时间是2023-12-20 13:24:30,天数365天,那么我们需要限制当前可选日期为2023-12-20 14时(不能选小于13:2…...

在MongoDB中使用数组字段和子文档字段进行索引
本文主要介绍在MongoDB使用数组字段和子文档字段进行索引。 目录 MongoDB的高级索引一、索引数组字段二、索引子文档字段 MongoDB的高级索引 MongoDB是一个面向文档的NoSQL数据库,它提供了丰富的索引功能来加快查询性能。除了常规的单字段索引之外,Mong…...
<JavaEE> 网络编程 -- 网络编程和 Socket 套接字
目录 一、网络编程的概念 1)什么是网络编程? 2)网络编程中的基本概念 1> 收发端 2> 请求和响应 3> 客户端和服务端 二、Socket套接字 1)什么是“套接字”? 2)Socket套接字的概念 3&…...

【计算机系统结构实验】实验2 流水线中的冲突实验
2.1 实验目的 加深对计算机流水线基本概念的理解; 理解MIPS结构如何用5段流水线来实现,理解各段的功能和基本操作; 加深对结构冲突/数据冲突/控制冲突的理解; 进一步理解解决数据冲突的方法,掌握如何应用定向技术来…...

conda环境下执行conda命令提示无法识别解决方案
1 问题描述 win10环境命令行执行conda命令,报命令无法识别,错误信息如下: PS D:\code\cv> conda activate pt conda : 无法将“conda”项识别为 cmdlet、函数、脚本文件或可运行程序的名称。请检查名称的拼写,如果包括路径&a…...
链接未来:深入理解链表数据结构(二.c语言实现带头双向循环链表)
上篇文章简述讲解了链表的基本概念并且实现了无头单向不循环链表:链接未来:深入理解链表数据结构(一.c语言实现无头单向非循环链表)-CSDN博客 那今天接着给大家带来带头双向循环链表的实现: 文章目录 一.项目文件规划…...

论文笔记 | Nature 2023 FunSearch:利用大语言模型在数学科学领域探索新的发现
文章目录 一、前言二、主要内容三、总结🍉 CSDN 叶庭云:https://yetingyun.blog.csdn.net/ 一、前言 科学中有许多难以解决的问题,这些问题难以获得确切解答,但却相对容易进行验证。在数学和计算机科学领域,这类问题被称为 NP 完全优化问题(NP-complete optimization pr…...

JavaScript 对象和 JSON 字符串的区别
JavaScript 对象和 JSON 字符串是两种不同的数据表示形式,它们有以下区别: 语法格式:JavaScript 对象是 JavaScript 语言中的一种数据类型,使用花括号 {} 包裹,属性和值之间使用冒号 : 分隔,并且使用逗号 …...

基于 Flink SQL 和 Paimon 构建流式湖仓新方案
目录 1. 数据分析架构演进 2. Apache Paimon 3. Flink + Paimon 流式湖仓 Consumer 机制 Changelog 生成编辑...
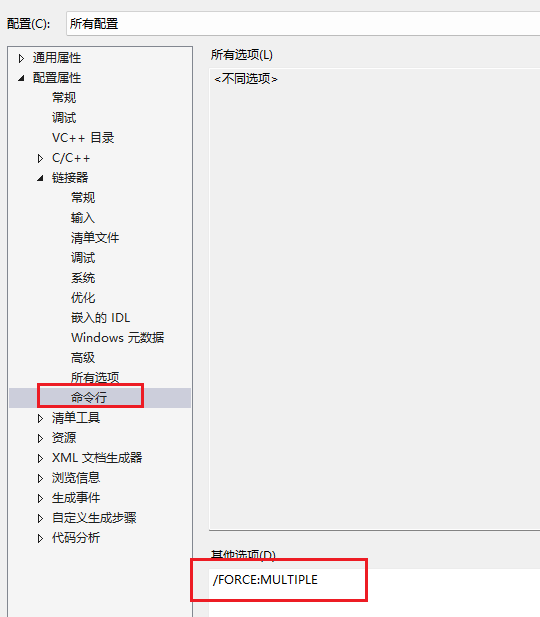
MFC静态链接+libtiff静态链接提示LNK2005和LNK4098
编译报错 1>msvcrt.lib(ti_inst.obj) : error LNK2005: "private: __thiscall type_info::type_info(class type_info const &)" (??0type_infoAAEABV0Z) 已经在 libcmtd.lib(typinfo.obj) 中定义 1>msvcrt.lib(ti_inst.obj) : error LNK2005: "pr…...
桶装水送水小程序:提升服务质量的利器
随着移动互联网的发展,越来越多的消费者通过手机在线购物和订购商品。如果你是一名桶装水供应商,想要拓展线上业务,那么开发一个桶装水微信小程序将是一个明智的选择。本文将指导你从零开始开发一个桶装水微信小程序,让你轻松完成…...

深度学习在训练什么,什么是模型
深度学习是机器学习的一个分支,它主要通过使用称为神经网络的复杂结构来学习数据的表征。在深度学习中,"训练"和"模型"是两个核心概念。 训练 在深度学习中,"训练"是指用数据来训练一个神经网络。这个过程涉…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...

用递归算法解锁「子集」问题 —— LeetCode 78题解析
文章目录 一、题目介绍二、递归思路详解:从决策树开始理解三、解法一:二叉决策树 DFS四、解法二:组合式回溯写法(推荐)五、解法对比 递归算法是编程中一种非常强大且常见的思想,它能够优雅地解决很多复杂的…...

2025-05-08-deepseek本地化部署
title: 2025-05-08-deepseek 本地化部署 tags: 深度学习 程序开发 2025-05-08-deepseek 本地化部署 参考博客 本地部署 DeepSeek:小白也能轻松搞定! 如何给本地部署的 DeepSeek 投喂数据,让他更懂你 [实验目的]:理解系统架构与原…...
