高级数据结构 ＜二叉搜索树＞

本文已收录至《数据结构(C/C++语言)》专栏！
作者：ARMCSKGT

---

---

前言

前面我们学习了二叉树，但仅仅只是简单的二叉树并没有很大的用处，而本节的二叉搜索树是对二叉树的升级，其查找效率相对于简单二叉树来说有一定提升，二叉搜索树是学习AVL树和红黑树的基础，所以我们必须先了解二叉搜索树。

---

正文

二叉搜索树的概念

---

二叉搜索树（Binary search tree）也称二叉排序树或二叉查找树，是在普通二叉树基础上的升级版本，普通二叉树的利用价值不大，而二叉搜索树要求 左节点比根小，右节点比根大，二叉搜索树将数据按二分性质插入在树中，所以将数据存入 二叉搜索树 中进行查找时，理想情况下只需要花费 logN 的时间（二分思想），此时使用中序遍历可以得到一列有序序列，因此 二叉搜索树 的查找效率极高，具有一定的实际价值。

二叉搜索树名字的由来就是因为搜索（查找）速度很快！

二叉搜索树基本特点
一棵二叉树，可以为空；如果不为空则：

• 如果左子树存在，则左子树根节点一定比根节点值要小
• 如果右子树存在，则右子树根节点一定比根节点值要大
• 左子树中的所有节点比根节点小，右子树中的所有节点比根节点大
• 所有的节点值都不相同，不会出现重复值的节点
• 所有子树都遵循这些性质

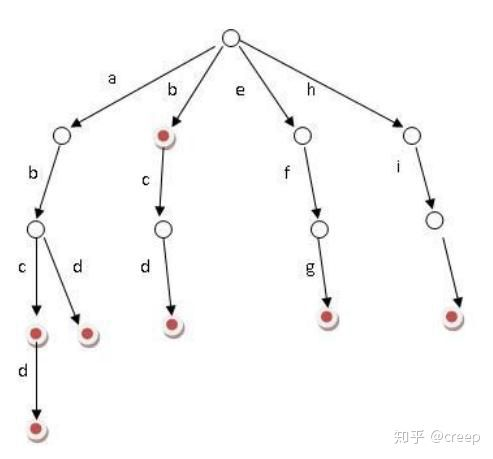
在这种性质下，使用中序遍历可以得到升序序列，如果将性质反转，即左比根大右比根小，则中序遍历可得到降序序列。

如上图的中树，中序遍历序列为：1 3 4 6 7 8 10 13 14

---

二叉搜索树的基本功能实现

---

二叉搜索树的基本框架

二叉搜索树的节点同样需要单独使用模板封装，且因为会用到比较函数，所以需要一个模板参数充当比较函数。

//节点类
template<class T>
struct TreeNode
{T _key;TreeNode<T>* _left;TreeNode<T>* _right;TreeNode():_key(T()), _left(nullptr), _right(nullptr){}TreeNode(const T& key):_key(key), _left(nullptr), _right(nullptr){}
};//默认比较函数
template<class T>
struct Compare
{bool operator()(const T& left, const T& right) { return left > right; }
};//二叉搜索树
template<class T, class Com = Compare<T>>
class BSTree
{//对节点类型 和 树类型 的重命名 方便使用using NodeType = TreeNode<T>; //相对于 typedef TreeNode<T> NodeType;using TreeType = BSTree<T, Com>; 
public:BSTree():_root(nullptr), _size(0){}
private:NodeType* _root; //根节点size_t _size;    //节点数量Com _com;        //比较函数
};

---

插入节点

对于插入函数，我们的目标是要找到合适的插入位置！

步骤

• 检查root根节点，如果根节点为空则直接赋值为根节点。
• 通过 key（插入值）参数查找最佳插入位置，如果遇到相等的，则返回false表示插入失败。
• 在查找时记录迭代变量cur的前驱节点parent，当迭代变量为nullptr时，记录的前驱节点就是合适插入节点，插入在该前驱节点后即可。
• 在链接插入时，比较插入值key与parent节点值的的大小，从而得知插入到左子树还是右子树，最终插入成功返回true。

代码实现(迭代版)：

bool Insert(const T& key)
{if (_root == nullptr){NodeType* newnode = new NodeType(key);_root = newnode;_size = 1;return true;}NodeType* parent = _root;NodeType* cur = _root;while (cur){parent = cur;//节点值小于keyif (_com(key, cur->_key)) cur = cur->_right;//节点值大于keyelse if (_com(cur->_key, key)) cur = cur->_left;else return false;}NodeType* newnode = new NodeType(key);//比较节点值key与parent节点值的大小，插入在正确的位置if (_com(key, parent->_key)) parent->_right = newnode;else parent->_left = newnode;++_size;return true;
}

注意：parent指针不能赋值为nullptr，当只有一个根节点时，插入会发生空指针访问！

当然，迭代可以实现插入，递归也可以，思想相同，但是实现上有一定差异。


关于递归版插入函数
因为有递归的存在，所以需要两个参数：一个用于查找的key和递归参数root节点地址。但是这个函数并不对外暴露，我们对外暴露的是一个key参数的函数，调用内部递归函数。
这里巧妙的是，我们传递的参数是对节点的引用，那么我们在当前递归函数中的修改，可以影响上一层的节点(父节点)。
假设当前节点为root，那么当我们递归root->left时，此时root参数变为root->left，我们修改root就是对上一层root->left修改，这样，当我们检查到root->left为nullptr时，创建新节点并构建链接关系然后返回即可完成插入新节点。
同样的，如果插入成功返回true，插入失败返回false。

代码实现(递归版)：

bool RecuInsert(const T& key) //递归插入-外部调用接口
{return _RecuInsert(key, _root);
}bool _RecuInsert(const T& key, NodeType*& root) //递归插入-实际调用函数
{//发现空节点直接链接 对节点的引用会自动完成对节点的链接if (root == nullptr){NodeType* newnode = new NodeType(key);root = newnode;return true;}//递归继续查找最佳插入位置if (_com(key, root->_key)) return _RecuInsert(key, root->_right);else if (_com(root->_key, key)) return _RecuInsert(key, root->_left);return false;
} 

可以发现，递归加持节点引用帮我们省去了很多麻烦，代码也很简洁，但迭代和递归各有优劣，我们都做介绍！

---

删除节点

对于删除函数，与插入类似，需要先查找值为key的节点，然后分情况删除。

步骤

• 通过key值从根节点开始遍历，寻找等值节点，cur逐个遍历节点，parent记录cur的前驱节点
• 如果根节点为nullptr或cur遍历为nullptr，则没有可删除的节点，返回false
• 如果找到节点，则开始分情况删除，删除后返回true

这里的难点是删除时，如何保证树的序列和链接关系，分为三种情况：

• 被删节点左右子树为空 (直接删除)
• 被删节点左子树或右子树为空 (托孤，将自己的子节点拜托给父节点管理)
• 被删节点左右子树都不为空 (找一个替代节点来管理)

实现代码(迭代版)：

bool Erase(const T& key)
{if (_root == nullptr) return false;//删除节点NodeType* parent = nullptr;NodeType* cur = _root;//找节点while (cur){//节点值小于keyif (_com(key, cur->_key)){parent = cur;cur = cur->_right;}//节点值大于keyelse if (_com(cur->_key, key)){parent = cur;cur = cur->_left;}else //找到了 开始删除{if (cur->_right == nullptr) //删除的节点只有左子树{NodeType* DelNode = cur;//改变链接关系//如果要删除的是根节点if (cur == _root) _root = cur->_left;else //非根节点{if (parent->_left == cur) parent->_left = cur->_left;else parent->_right = cur->_left;}delete DelNode;}else if (cur->_left == nullptr) //删除的节点只有右子树{NodeType* DelNode = cur;//改变链接关系//如果要删除的是根节点if (cur == _root) _root = cur->_right;else //非根节点{if (parent->_left == cur) parent->_left = cur->_right;else parent->_right = cur->_right;}delete DelNode;}else //子节点都在{//找替代 左子树的最大节点(最右节点) 右子树的最小节点(最左节点)//去左子树中找最大节点//NodeType* maxParent = cur;//NodeType* maxLeft = cur->_left;//while (maxLeft->_right)//{//	maxParent = maxLeft;//	maxLeft = maxLeft->_right;//}//cur->_key = maxLeft->_key;接管替代节点的右孩子//if (maxParent->_left == maxLeft) maxParent->_left = maxLeft->_left;//else maxParent->_right = maxLeft->_left;//delete maxLeft;//去右子树中找最小节点NodeType* minParent = cur;NodeType* minRight = cur->_right;while (minRight->_left){minParent = minRight;minRight = minRight->_left;}cur->_key = minRight->_key;//接管替代节点的右孩子if (minParent->_left == minRight) minParent->_left = minRight->_right;else minParent->_right = minRight->_right;delete minRight;}--_size;return true;}}return false; //找不到节点
}

将代码结合下图理解，就能知道这些情况到底在干什么了。


被删节点只有左子树或右子树时：
我们只需要让被删节点的父节点托管子节点即可，即让爷爷节点接管孙子节点。
>注意：如果被删节点是根节点，还需要特殊处理，修改根节点_root的值。

被删节点左右子树都存在：
此时我们需要找一个替代节点来接管左右子树，接管节点必须保证接管后树的整体形态和性质不变。
于是我们可以选择左子树中的最大节点(maxLeft) 或 右子树中的最小节点(minRight)，两个节点中的其中一个，将该节点值覆盖被删节点的值转而删除该节点即可，该替代节点一定是叶子节点，可以转换为直接删除。
因为 左子树的最大节点 小于和最接近 当前根节点 ，右子树中的最小节点大于和最接近。
所以我们在删除节点前，需要寻找合适的替代节点来接管左右孩子，维护树的形态，在寻找合适节点时，需要 记录替代节点的前驱节点，在被删除后及时更新替代节点父节点的链接关系。

这里我们并不是实际删除了11节点，而是采用伪删除法，替换节点值，转而删除替代节点。
这里使用伪删除法，将问题转化为删除叶子节点，省去了很多麻烦！


关于递归版删除函数
同样的，递归函数需要在内部单独实现，外部对递归函数重新封装。
我们在插入函数中使用对节点地址的引用解决了很多问题，同样的，在删除函数中，我们也使用了对节点的引用，这样可以做到 在不同的栈帧中，删除同一个节点，而非临时变量，同时递归删除还用到了一种思想：转换问题的量级。

因为是对节点的引用，所以当我们遍历到被删节点时，先记录被删除节点的地址，因为是对节点的引用，则在节点数大于1的情况下，当前函数中的root节点地址必然是对某根节点的左子树节点或右子树节点的引用，我们对其做出修改会直接影响链接关系，如果被删节点只有左子树或右子树，直接将其左子树或右子树赋值给当前函数中root即可，然后删除记录的节点，如果被删节点左右子树都存在，则同样需要找左子树最大节点或右子树最小节点作为替代节点，因为节点值交换了，所以被删节点转换成了替代节点，所以继续调用递归删除替代节点即可。

实现代码(递归版)：

bool RecuErase(const T& key) //递归删除-外部接口
{return _RecuErase(key, _root);
}bool _RecuErase(const T& key, NodeType*& root) //递归删除-实际调用函数
{if (root == nullptr) return false;//节点值比key小，递归去右子树中寻找 否则去左子树中寻找if (_com(key, root->_key)) return _RecuErase(key, root->_right);else if (_com(root->_key, key)) return _RecuErase(key, root->_left);else //找到了{NodeType* delNode = root; //记录要删除的节点if (root->_left == nullptr) root = root->_right;else if (root->_right == nullptr) root = root->_left;else //两个子节点都存在{//找一个替代//找左边的最大节点NodeType* cur = root->_left;while (cur->_right) cur = cur->_right;//找右边的最小节点//NodeType* cur = root->_right;//while (cur->_left) cur = cur->_left;//将要删除的值与替代节点交换T tmp = root->_key;root->_key = cur->_key;cur->_key = tmp;return _RecuErase(key, root->_left); //转而删除子节点//return _RecuErase(key, root->_right); //转而删除子节点}delete delNode;return true;}return false;
}

关于删除需要注意的：

• 涉及更改链接关系的操作，都需要保存父节点的信息
• 左右子树都为空时，表示删除根节点root，此时 parent 为空，不必更改父节点链接关系，更新根节点root的信息后，删除目标节点即可，这种情况需要特殊处理。
• 左右子树都不为空时，parent 要初始化为 cur，避免后面的野指针或空指针的问题。
  

删除函数细节比较多，需要结合代码多多理解！
关于搜索二叉树的删除函数，还有一道题，大家可以尝试：删除二叉搜索树中的节点

---

查找函数

查找函数相对比较简单，一个变量cur向下遍历即可。

步骤

• 当cur节点值小于key时cur走向右子树，大于则走向左子树
• 当cur遍历到值为key的节点时返回true
• 当根节点root或cur遍历到nullptr时，表示树中不存在该节点，返回false
  

实现代码(迭代版)：

		bool Find(const T& key){if (_root == nullptr) return false;NodeType* cur = _root;while (cur){if (_com(key, cur->_key)) cur = cur->_right;else if (_com(cur->_key, key)) cur = cur->_left;else return true;}return false;}

关于递归版查找函数
递归版查找函数也需要实现一个内部的递归函数，然后使用外部调用接口封装。
同样的，查找节点也有递归版本，其实现比较简单，当root小于key时递归遍历其右子树，大于则遍历其左子树，等于时返回true，root为nullptr时，返回false。

实现代码(递归版)：

bool RecuFind(const T& key) //删除函数-外部接口
{return _RecuFind(key, _root);
}bool _RecuFind(const T& key, NodeType* root) //删除函数-实际调用函数
{if (root == nullptr) return false;if (_com(key, root->_key)) return _RecuFind(key, root->_right);else if (_com(root->_key, key)) return _RecuFind(key, root->_left);else return true;return false;
}

---

中序遍历函数

中序遍历函数会变遍历边打印，最终打印出的节点序列成有序。
这个函数比较简单，我们在第一次接触二叉树时就已经接触到了，但是因为我们需要递归，所有需要在内部实现一个递归函数，使用外部接口调用即可。

void MidBfd() //中序遍历-外部接口
{_MidBfd(_root);cout << endl;
}void _MidBfd(NodeType* root) //中序遍历-实际调用函数
{if (root == nullptr) return;_MidBfd(root->_left);cout << root->_key << " ";_MidBfd(root->_right);
}

乱序插入后，中序遍历打印有序。

---

析构函数和销毁函数(后序遍历销毁)

销毁一棵二叉树，我们需要先销毁子树再销毁根节点，那么后序遍历再合适不过了。
因为销毁函数需要后序遍历，递归销毁，所以我们需要单独封装一个带节点指针参数的递归函数来销毁树。
当析构函数在析构时调用销毁函数后置空根节点指针即可！

~BSTree() //析构函数
{Destroy(_root);_root = nullptr;
}void Destroy(NodeType* root) //后序销毁
{if (root == nullptr) return;Destroy(root->_left);Destroy(root->_right);delete root;
}

---

拷贝构造和赋值重载(前序遍历创建)

编译器默认的拷贝构造默认是浅拷贝，当浅拷贝根节点指针后销毁时便会出现异常。

递归拷贝函数： 所以我们必须实现一个可以拷贝一棵树且返回根节点地址的函数，这个函数我们采用前序遍历，前序遍历一棵树，每遍历一个节点就创建一个节点然后递归创建其左子树和右子树，最后返回根节点地址。

拷贝构造函数：我们只需要调用拷贝函数拷贝另一棵树然后将根节点地址赋值给本对象的_root即可(实现了拷贝构造函数就必须实现一个默认构造函数)。

赋值重载函数：我们重新赋值一棵树时需要先销毁当前对象的树，再调用拷贝函数拷贝这棵树，不过这样做显得很繁琐。我们可以将赋值重载函数参数改为传值传参，这样传值传参会调用拷贝构造拷贝一棵临时的树，然后我们调用swap将我们需要赋值树的节点地址交换，就完成了，当函数执行完成，临时变量会调用析构函数销毁树，因为我们把原来的树交换给了临时变量对象，所以临时变量会帮我们销毁而不需要我们自己销毁，这样就节省了我们的操作步骤。

实现代码：

BSTree(const TreeType& bst) //拷贝构造:_root(nullptr), _size(0)
{_root = Copy(bst._root);_size = bst._size;
}TreeType& operator=(TreeType bst) //赋值重载
{swap(bst); //我们自己实现的交换函数return *this;
}NodeType* Copy(const NodeType* root) //前序拷贝一棵树
{if (root == nullptr) return nullptr;NodeType* newnode = new NodeType(root->_key);newnode->_left = Copy(root->_left);newnode->_right = Copy(root->_right);return newnode;
}

---

其他函数

剩下的函数是比较简单的基础函数：

• 获取节点数量
• 交换函数
• 清空节点

size_t size() { return _size; }void swap(TreeType& bst) //交换函数
{//也可以调用库中的swapNodeType* root = bst._root;bst._root = _root;_root = root;Com com = bst._com;bst._com = _com;_com = com;size_t sz = bst._size;bst._size = _size;_size = sz;
}void clear() //清空节点
{Destroy(_root);_root = nullptr;
}

---

二叉搜索树的应用场景

---

二叉搜索树凭借着极快的查找速度，有着一定的实战价值，常用的查找模型是 key查找模型和 key / value 查找模型 及 存储模型。

---

key模型

key模型其实就是我们上面实现的树，节点中只有一个值，一般适用于在集合中查找某个参数在不在！

应用场景：

• 门禁系统
• 单词拼写检查
• . . . . . .
  
  

//简易字典
int main()
{BSTree<string> bst;bst.Insert("中国");bst.Insert("CSDN");bst.Insert("BIT");bst.Insert("C++");bst.Insert("668");while (true){string tmp;cout << "请输入>>> ";cin >> tmp;if (bst.Find(tmp)) cout << "在词典中" << endl;else cout << "不在词典中" << endl;}return 0;
';;}

单值key的意义本身就是判断在不在，判断在不在也需要查找，二叉搜索树比较合适。

---

key-value模型

key-value模型需要存储两个值，其中用来对比(插入删除的依据)的是key，同时存储value (仅存储，value没用任何其他意义) 建立key-value的映射关系，这是一种典型的哈希思想。


应用场景：

• 电话号码查询快递信息
• 词典互译
• . . . . . .
  
  

我们将key模型的代码微微改动就可以实现key-value模型的二叉搜索树。
这里我们简单实现一下。

//二叉搜索树KV
template<class KT, class VT, class Com = Compare<KT>>
class KVBSTree
{using NodeType = TreeNode<pair<KT, VT>>;using TreeType = KVBSTree<KT, VT, Com>;
public:KVBSTree():_root(nullptr), _size(0){}KVBSTree(const TreeType& bst):_root(nullptr), _size(0){_root = Copy(bst._root);_size = bst._size;}TreeType& operator=(TreeType bst){swap(bst); //我们自己实现的交换函数return *this;}bool Insert(const KT& key, const VT& value){if (_root == nullptr){NodeType* newnode = new NodeType({ key,value });_root = newnode;_size = 1;return true;}NodeType* parent = _root;NodeType* cur = _root;while (cur){parent = cur;//节点值小于keyif (_com(key, cur->_key.first)) cur = cur->_right;//节点值大于keyelse if (_com(cur->_key.first, key)) cur = cur->_left;else return false;}NodeType* newnode = new NodeType({ key,value });if (_com(key, parent->_key.first)) parent->_right = newnode;else parent->_left = newnode;++_size;return true;}bool Erase(const KT& key){if (_root == nullptr) return false;//删除节点NodeType* parent = nullptr;NodeType* cur = _root;//找节点while (cur){//节点值小于keyif (_com(key, cur->_key.first)){parent = cur;cur = cur->_right;}//节点值大于keyelse if (_com(cur->_key.first, key)){parent = cur;cur = cur->_left;}else //找到了 开始删除{if (cur->_right == nullptr) //删除的节点只有左子树{NodeType* DelNode = cur;//改变链接关系//如果要删除的是根节点if (cur == _root) _root = cur->_left;else //非根节点{if (parent->_left == cur) parent->_left = cur->_left;else parent->_right = cur->_left;}delete DelNode;}else if (cur->_left == nullptr) //删除的节点只有右子树{NodeType* DelNode = cur;//改变链接关系//如果要删除的是根节点if (cur == _root) _root = cur->_right;else //非根节点{if (parent->_left == cur) parent->_left = cur->_right;else parent->_right = cur->_right;}delete DelNode;}else //子节点都在{//找替代 左子树的最大节点(最右节点) 右子树的最小节点(最左节点)//去左子树中找最大节点//NodeType* maxParent = cur;//NodeType* maxLeft = cur->_left;//while (maxLeft->_right)//{//	maxParent = maxLeft;//	maxLeft = maxLeft->_right;//}//cur->_key = maxLeft->_key;接管替代节点的右孩子//if (maxParent->_left == maxLeft) maxParent->_left = maxLeft->_left;//else maxParent->_right = maxLeft->_left;//delete maxLeft;//去右子树中找最小节点NodeType* minParent = cur;NodeType* minRight = cur->_right;while (minRight->_left){minParent = minRight;minRight = minRight->_left;}cur->_key = minRight->_key;//接管替代节点的右孩子if (minParent->_left == minRight) minParent->_left = minRight->_right;else minParent->_right = minRight->_right;delete minRight;}--_size;return true;}}return false; //找不到节点}pair<pair<KT, VT>, bool> Find(const KT& key) //key-value模型 通过key找value{//这里使用pair再套一层pair，用于返回查询的结果是否有效//false表示查询返回值无效if (_root == nullptr) return { {},false };NodeType* cur = _root;while (cur){if (_com(key, cur->_key.first)) cur = cur->_right;else if (_com(cur->_key.first, key)) cur = cur->_left;else return { cur->_key,true };}return { {},false };}size_t size() { return _size; }void swap(TreeType& bst) //交换函数{//也可以调用库中的swapNodeType* root = bst._root;bst._root = _root;_root = root;Com com = bst._com;bst._com = _com;_com = com;size_t sz = bst._size;bst._size = _size;_size = sz;}void clear() //清空节点{Destroy(_root);_root = nullptr;}//中序遍历打印void MidBfd(){_MidBfd(_root);cout << endl;}~KVBSTree(){Destroy(_root);_root = nullptr;}private://前序拷贝一棵树NodeType* Copy(const NodeType* root){if (root == nullptr) return nullptr;NodeType* newnode = new NodeType(root->_key);newnode->_left = Copy(root->_left);newnode->_right = Copy(root->_right);return newnode;}//中序void _MidBfd(NodeType* root){if (root == nullptr) return;_MidBfd(root->_left);cout << root->_key.first << " : " << root->_key.second << endl;_MidBfd(root->_right);}//后序销毁void Destroy(NodeType* root){if (root == nullptr) return;Destroy(root->_left);Destroy(root->_right);delete root;}private:NodeType* _root; //根节点size_t _size;       //节点数量Com _com;        //比较函数
};

关于pair：
pair是C++自带的一个用于存储key-value的对象。

还有一个函数make_pair，传递两个参数(key / value)，快速构建pair对象。

简易词典：

int main() 
{ KVBSTree<string, string> bst;bst.Insert("china", "中国");bst.Insert("fruit", "水果");bst.Insert("god", "神");bst.Insert("great", "伟大");bst.Insert("blue", "蓝色");while (true){string str;cout << "请输入>>> ";cin >> str;auto ret = bst.Find(str);if (ret.second) cout << ret.first.first << " : " << ret.first.second << endl;else cout << "词典中没有该词!" << endl;}return 0; 
}

---

关于二叉搜索树

---

本章介绍了最基本的二叉搜索树，因为其左右性质，其查找速度很快。

关于二叉搜索树的时间复杂度：最快 O(logn)，最慢 O(n)

我们仔细分析可以发现，当二叉搜索树插入有序序列时，会变成链表！

当二叉搜索树的高度等于节点数，则查找速度就是O(n)
为了解决这个问题，大佬们发明了 AVL树 和 红黑树 等，降低二叉搜索树的高度，以加速查找。

AVL树 和 红黑树 的时间复杂度近似为：O(logn)
后面我们将详细介绍！

---

最后

本节我们介绍了二叉搜索树，讲解了二叉搜索树的相关概念，为后面AVL树和红黑树的学习做铺垫，本节我们只是实现了最基本的代码，在AVL树和红黑树中，我们将实现更多功能，来完善我们的二叉搜索树。

本次 <二叉搜索树> 就先介绍到这里啦，希望能够尽可能帮助到大家。

如果文章中有瑕疵，还请各位大佬细心点评和留言，我将立即修补错误，谢谢！

本节涉及代码：二叉搜索树博客代码

🌟其他文章阅读推荐🌟
数据结构初级＜二叉树＞
C++ <继承>
C++ <STL容器适配器>
Linux进程间通信
Linux软硬链接和动静态库
🌹欢迎读者多多浏览多多支持!🌹