P8074 [COCI2009-2010#7] SVEMIR 最小生成树
[COCI2009-2010#7] SVEMIR
题目描述
太空帝国要通过建造隧道来联通它的 NNN 个星球。
每个星球用三维坐标 (xi,yi,zi)(x_i,y_i,z_i)(xi,yi,zi) 来表示,而在两个星球 A,BA,BA,B 之间建造隧道的价格为 min{∣xA−xB∣,∣yA−yB∣,∣zA−zB∣}\min\{|x_A-x_B|,|y_A-y_B|,|z_A-z_B|\}min{∣xA−xB∣,∣yA−yB∣,∣zA−zB∣}。
现要建造 N−1N-1N−1 条隧道使得所有的星球都能直接或间接相连。求完成该任务所需的最小总价。
输入格式
第一行,一个整数 NNN。
接下来的 NNN 行,每行三个整数 xi,yi,zix_i,y_i,z_ixi,yi,zi,表示第 iii 个星球的坐标。
数据保证不存在两个具有相同坐标的星球。
输出格式
输出所需的最小总价。
样例 #1
样例输入 #1
2
1 5 10
7 8 2
样例输出 #1
3
样例 #2
样例输入 #2
3
-1 -1 -1
5 5 5
10 10 10
样例输出 #2
11
样例 #3
样例输入 #3
5
11 -15 -15
14 -5 -15
-1 -1 -5
10 -4 -1
19 -4 19
样例输出 #3
4
提示
【数据规模与约定】
- 对于 100%100\%100% 的数据,1≤N≤1051 \le N \le 10^51≤N≤105,−109≤xi,yi,zi≤109-10^9 \le x_i,y_i,z_i \le 10^9−109≤xi,yi,zi≤109。
【提示与说明】
题目译自 COCI 2009-2010 CONTEST #7 Task 4 SVEMIR。
本题分值按 COCI 原题设置,满分 100100100。
最小生成树,如果把每两个点之间的边都存储,会超时超空间。
放宽条件,问题等价于每个点之间有三条边,边权分别是|x1-x2|,|y1-y2|,|z1-z2|,然后求最小生成树距离。
所以观察规律,如果按x排序,只用在相邻次序的点之间建立x插值边,分析得知相隔的点对pi,pk (|i-k|!=1)建立的x差值边一定用不上(如果这两点在两棵树上,想要连通这两棵树,选择x差值边,一
定不如它们中间一点到其中某一点的x差值边来得好)。
按照y和z排序同理。
#include <bits/stdc++.h>
#define for0(a,n) for(int (a)=0;(a)<(n);(a)++)
#define for1(a,n) for(int (a)=1;(a)<=(n);(a)++)
typedef long long ll;using namespace std;const int maxn=1e5+0.5;
int m,n;
ll ans;
int pre[maxn+5];
struct Edge
{int u,v,w;Edge(){}Edge(int u,int v,int w):u(u),v(v),w(w){}bool operator<(const Edge & e) const{return w<e.w;}};
vector<Edge>edges;struct Node
{int x,y,z,idx;bool operator <(const Node & b) const{return x<b.x;}
} nodes[maxn+5];bool cmp_y(Node & a, Node & b) {return a.y<b.y;}
bool cmp_z(Node & a, Node & b) {return a.z<b.z;}void init()
{m=0;edges.clear();ans=0;for0(i,n+1) pre[i]=i;
}int findroot(int x) {return pre[x]==x?x: pre[x]= findroot(pre[x]);}
bool merge(int &x,int &y)
{int rootx=findroot(x);int rooty=findroot(y);if (rootx==rooty) return false;pre[rootx]=rooty;return true;
}int main()
{std::ios::sync_with_stdio(false);while(cin>>n){for1(i,n){cin>>nodes[i].x>>nodes[i].y>>nodes[i].z;nodes[i].idx=i;}init();sort(nodes+1,nodes+n+1);// for1(i,n)
// {
// cout<<nodes[i].x<<" "<<nodes[i].y<<" "<<nodes[i].z;
// }for1(i,n-1){int dis=abs(nodes[i].x-nodes[i+1].x);edges.push_back( Edge(nodes[i].idx,nodes[i+1].idx,dis));}sort(nodes+1,nodes+n+1,cmp_y);for1(i,n-1){int dis=abs(nodes[i].y-nodes[i+1].y);edges.push_back( Edge(nodes[i].idx,nodes[i+1].idx,dis));}sort(nodes+1,nodes+n+1,cmp_z);for1(i,n-1){int dis=abs(nodes[i].z-nodes[i+1].z);edges.push_back( Edge(nodes[i].idx,nodes[i+1].idx,dis));}sort(edges.begin(),edges.end());m=edges.size();// for0(i,m)
// {
// cout<<edges[i].u<<" "<<edges[i].v<<" "<<edges[i].w<<endl;
// }int T=n-1;for0(i,m){Edge & e = edges[i];int u=e.u,v=e.v,w=e.w;if(!merge(u,v)) continue;ans+= w;if (--T==0) break;}printf("%lld\n",ans);}return 0;
}
/*
2
1 5 10
7 8 23
-1 -1 -1
5 5 5
10 10 105
11 -15 -15
14 -5 -15
-1 -1 -5
10 -4 -1
19 -4 19
*/
相关文章:

P8074 [COCI2009-2010#7] SVEMIR 最小生成树
[COCI2009-2010#7] SVEMIR 题目描述 太空帝国要通过建造隧道来联通它的 NNN 个星球。 每个星球用三维坐标 (xi,yi,zi)(x_i,y_i,z_i)(xi,yi,zi) 来表示,而在两个星球 A,BA,BA,B 之间建造隧道的价格为 min{∣xA−xB∣,∣yA−yB∣,∣zA−zB∣}\min\{|x_A-x_…...

10种常见网站安全攻击手段及防御方法
在某种程度上,互联网上的每个网站都容易遭受安全攻击。从人为失误到网络罪犯团伙发起的复杂攻击均在威胁范围之内。 网络攻击者最主要的动机是求财。无论你运营的是电子商务项目还是简单的小型商业网站,潜在攻击的风险就在那里。 知己知彼百战不殆&…...

为什么我选择收费的AdsPower指纹浏览器?
在决定开始用指纹浏览器之前,龙哥让我们团队的运营小哥找了市面上很多产品去测试。最后,还是决定用AdsPower。每个人的使用感受都不一样,龙哥就说说几个用得顺手的几个点。一、指纹环境强大 双内核引擎 市面上指纹浏览器内核都是基于谷歌Chro…...

Java输入输出和数组
一、问答题 1. 如何声明和创建一个一维数组? Int i[]new int[3] 2. 如何访问数组的元素? Int a[]new int a[3] for (int x0;x<a.length;x){ System.out.print(i[x]); } System.out.println(); 3.数组下标的类型是什么?最小的下标是什…...

这些免费API帮你快速开发,工作效率杠杠滴
一、短信发送 短信的应用可以说是非常的广泛了,短信API也是当下非常热门的API~ 短信验证码:可用于登录、注册、找回密码、支付认证等等应用场景。支持三大运营商,3秒可达,99.99%到达率,支持大容量高并发。…...

干货|最全PCB布线教程总结,14条PCB布线原则技巧,保姆级搞定PCB布线
1、坚持手动布线,慎用自动布线2、了解制造商的规格3、合适的走线宽度4、迹线之间留出足够的空间5、元器件放置6、保持模拟和数字走线分开7、接地层8、走线和安装孔留有足够的空间9、交替走线方向10、避免电容耦合11、放置散热孔和焊盘12、接地和电源走线13、利用丝印…...

编程快捷键和markdown语法小计
Data Structure FQA文章目录1.idea快捷键汇总2.markdown一些常用语法1.idea快捷键汇总 altenter 快捷生成变量 altInsert可以新建类,文件,get或set方法,此快捷键又名创造一切 编辑区和文件区的跳转。 alt 1 :编辑区跳转至…...
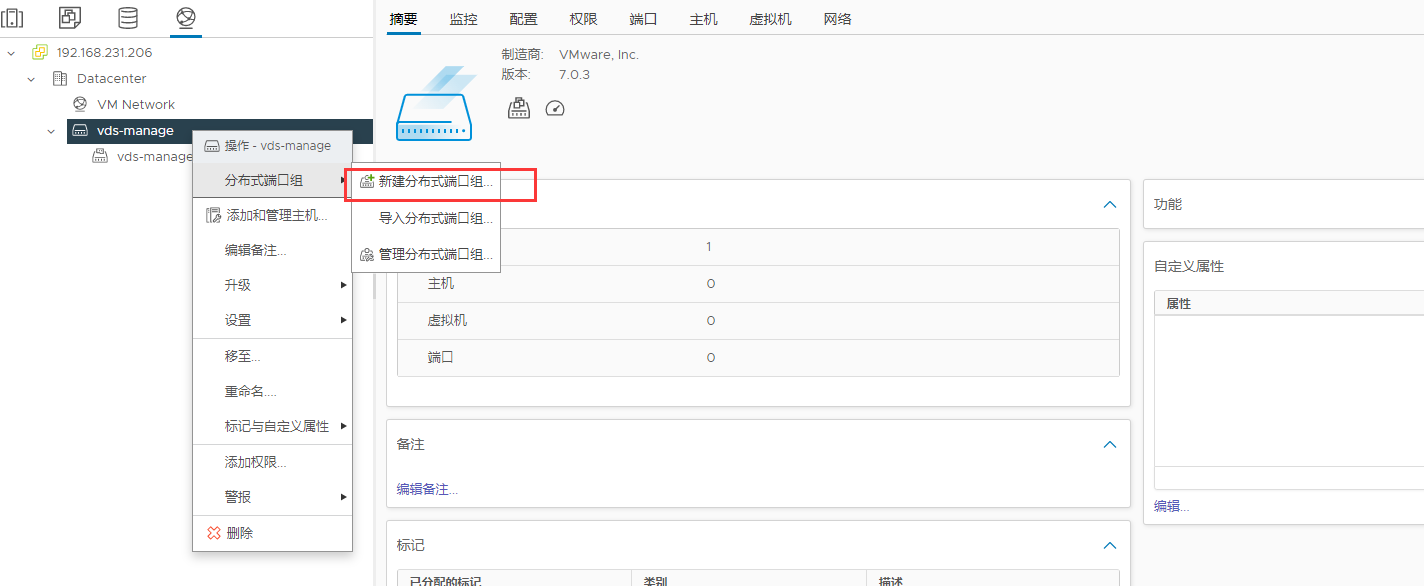
内网vCenter部署教程二,最全的了!
一、组网说明 vCenter组网最佳实践 每台服务器需要6个网口,需要三个分布式交换机,每个交换机分配2个物理网卡做冗余,分别做为管理网络、业务网络、高可用网络使用。另vsan网络和vmotion网络可以复用业务网络或管理网络,vcenter HA需要单独用一个网络。 二、创建管理网络…...

2023-3-2 刷题情况
迷宫 题目描述 这天, 小明在玩迷宫游戏。 迷宫为一个 nn 的网格图, 小明可以在格子中移动, 左上角为 (1,1), 右 下角 (n,n) 为终点。迷宫中除了可以向上下左右四个方向移动一格以外, 还有 m 个双向传送门可以使用, 传送门可以连接两个任意格子。 假如小明处在格子 (x1,y1)(…...
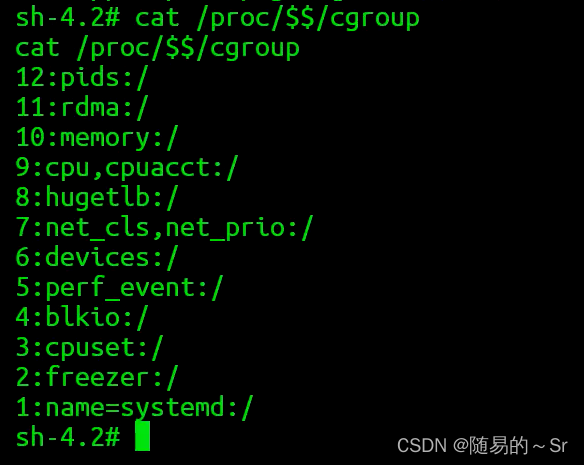
Docker SYS_ADMIN 权限容器逃逸
1.漏洞原理Docker容器不同于虚拟机,它共享宿主机操作系统内核。宿主机和容器之间通过内核命名空间(namespaces)、内核Capabilities、CGroups(control groups)等技术进行隔离。若启动docker容器时给主机一个--cap-addSY…...

【Kotlin】 yyyy-MM-dd HH:mm:ss 时间格式 时间戳 全面解读超详细
时间格式 时间格式(协议)描述gg时期或纪元。y不包含纪元的年份。不具有前导零。yy不包含纪元的年份。具有前导零。yyyy包含纪元的四位数的年份。M月份数字。一位数的月份没有前导零。MM月份数字。一位数的月份有一个前导零。MMM月份的缩写名称,在AbbreviatedMonthN…...

git repack多包使用及相关性能测试
1、git数据结构 git 中存在四种数据结构,即object包含四种,分别是tree对象、blob对象、commit对象、tag对象 1.1 blob对象 存储文件内容,内容是二进制的形式,通过SHA-1算法对文件内容和头信息进行计算得到key(文件名)。 如果一…...
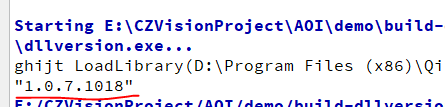
QT获取dll库文件详细信息
一、需求背景获取软件下依赖的dll库的版本信息,如下图所示版本为1.0.7.1018二、实现方法2.1步骤windows下实现,基于version.lib(version.dll)提供的函数获取这些信息首先使用GetFileVersionInfoSizeA(W)获取VersionInfo的大小,申请缓冲区&…...

常见的电脑运行卡顿原因及解决方法
大家在日常使用电脑过程中,会发现多开几个文件就卡顿,其实很多时候都跟C盘长期不清理有关,C盘的内存被下载的软件安装包、页面文件、休眠文件、更新文件等一系列的文件占据。大的文件甚至能占到20-30G,驱动人生就为大家带来几种解…...

案例08-让软件的使用者成为软件的设计者
一:背景介绍 对于需求的开发每天可能都会有上线的情况,为了防止每次上线拉取代码或者修改配置而引发的冲突以及发生了冲突应该找谁一起确定一下代码留下那一部分的情况。所以在开发的群中会有一个表格来记录每个需求上线修改的环境、是否修改数据库、是否…...

QinQ与Vlan Mapping讲解
目录 QinQ Vlan扩展 QinQ实现方式 QinQ实验配置 Vlan Mapping Vlan映射 映射方式 配置命令 QinQ Vlan扩展 QinQ全称为802.1Q-in-802.1Q,为Vlan扩展技术,在802.1Q标签报文的基础上再增加一层802.1Q标签,实现扩展Vlan空间;可…...

golang 获取token方法
package main import ( "fmt" "time" "github.com/dgrijalva/jwt-go" ) const ( SECRETKEY "202203021124355xxx" //私钥 ) // 自定义 Claims type CustomClaims struct { UserId int64 jwt.StandardClaims } func main() { //生…...
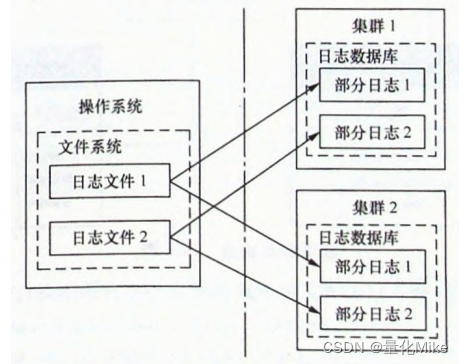
【数据库专题】数据库Mongodb之深入认知云计算三种服务方式、mongodb特点、mongodb重要进程 mongod、mongo、其他进程区别
文章目录一、什么是云计算1. IaaS:基础设施即服务2. SaaS:软件即服务3. PaaS:平台即服务二、大数据与云计算关系三、什么是MongoDB四、大数据与MongoDB五、MongoDB特点六、安装MongoDB七、重要进程介绍7.1 mongod进程7.2 mongo进程7.3 其他进程7.3.1 mongodump重建数据库7.3.2 …...
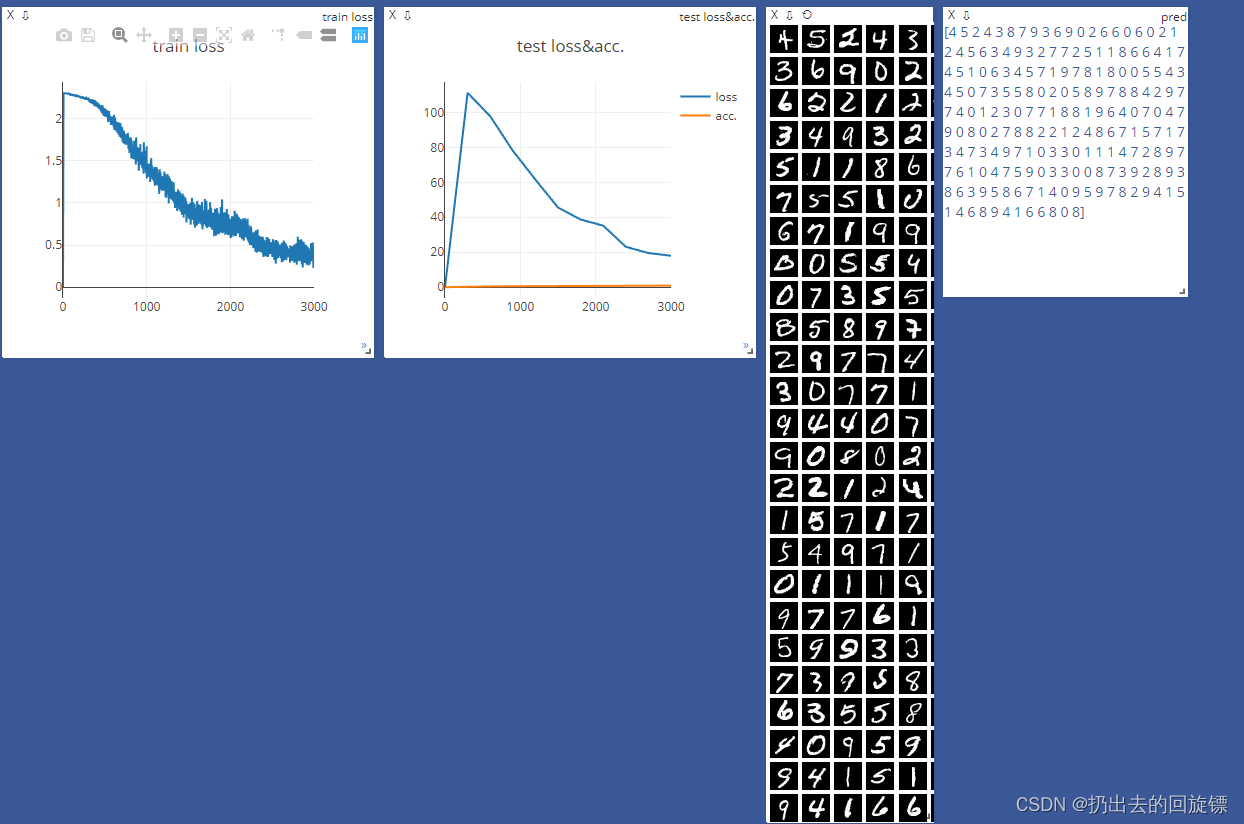
ccc-pytorch-小实验合集(4)
文章目录一、 Himmelblau 优化二、多分类实战-Mnist三、Sequential与CPU加速-Mnist四、visidom可视化一、 Himmelblau 优化 Himmelblau 是一个具有4个最优值的2维目标函数。其函数和最优值点如下: 图象绘制: import numpy as np from matplotlib impo…...

webrtc音频系列——4、RTP与RTCP协议
如果让你从0开发一套实时互动直播系统,你首先要选择网络传输协议。UDP 还是 TCP?答案是:UDP。为什么实时传输不能用 TCP ?TCP 的目的就是实现数据的可靠传输,因此他有一套 握手,发送 -> 确认,…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...
