【算法】【动规】回文串系列问题
文章目录
- 跳转汇总链接
- 3.1 回文子串
- 3.2 最长回文子串
- 3.3 分割回文串 IV
- 3.4 分割回文串II(hard)
跳转汇总链接
👉🔗动态规划算法汇总链接
3.1 回文子串
🔗题目链接
给定一个字符串 s ,请计算这个字符串中有多少个回文子字符串。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
- 状态表示
- dp[i][j] 表示字符串 s 中以 i 位置开头 j 位置结尾的子串,是否是回文。
- 状态转移方程
-
分析 dp 表,要判断 [i, j] 位置的子串是否为回文,首先要根据 s[i] 和 s[j] 的大小判定,具体如下:
s[i] != s[j], false s[i] == s[j], i == j, truei + 1 == j, truej - i > 1, s[i+1][j-1] == true, trues[i+1][j-1] == false, false
-
- 初始化
- 这里主要是[i+1][j-1] 可能会超出需要范围,但是有个隐含条件 i <= j,可以在 for 循环中控制,所以不需要初始化。
- 填表顺序
- 填写 dp[i][j],需要有 [i+1] 和 [j-1],故二维数组从下往上填写。
- 返回值
- dp 中的 true 的出现次数。
🐎代码如下:
class Solution {
public:int countSubstrings(string s) {int n = s.size();vector<vector<bool>> dp(n, vector<bool>(n));int ret = 0;for(int i = n - 1; i >= 0; i--){for(int j = i; j < n; j++){// 默认都是 false,只需要处理 true 的位置if(s[i] == s[j])dp[i][j] = i + 1 < j ? dp[i+1][j-1] : true;if(dp[i][j])ret++;}}return ret;}
};
3.2 最长回文子串
🔗题目链接
给你一个字符串 s,找到 s 中最长的回文子串。
如果字符串的反序与原始字符串相同,则该字符串称为回文字符串。
如上题分析,写 dp 方程。
在 dp[i][j] 且满足基本约束时,找到 len(即 j - i + 1)的最大值,
同时,由于 dp 表是从下往上(从后往前)填的,正好更新 begin。
🐎代码如下:
class Solution {
public:string longestPalindrome(string s) {int n = s.size();int len = 1, begin = 0;vector<vector<bool>> dp(n, vector<bool>(n));for(int i = n - 1; i >= 0; i--){for(int j = i; j < n; j++){if(s[i] == s[j])dp[i][j] = i+1 < j ? dp[i+1][j-1] : true;if(dp[i][j] && j-i+1 > len)len = j - i + 1, begin = i;}}return s.substr(begin, len);}
};
3.3 分割回文串 IV
🔗题目链接
给你一个字符串 s ,如果可以将它分割成三个 非空 回文子字符串,那么返回 true ,否则返回 false 。
当一个字符串正着读和反着读是一模一样的,就称其为 回文字符串 。
还是照上述方法,生成 dp 表,记录是否为回文子串,进行数据预处理;
再将字符分成三部分,依次遍历,如果 相应位置的 dp 值为 true,就可以直接返回啦。
🐎代码如下:
class Solution {
public:bool checkPartitioning(string s) {int n = s.size();// 1. 预处理:子串是否是回文vector<vector<bool>> dp(n, vector<bool>(n));for(int i = n - 1; i >= 0; i--)for(int j = i; j < n; j++)if(s[i] == s[j])dp[i][j] = i+1 < j ? dp[i+1][j-1] : true;// 2. 字符串分成三段,枚举就好了// [0, i) [i, j) [j, n)for(int i = 1; i < n - 1; i++) // i 是第二段的起始for(int j = i + 1; j < n; j++) // j 是第三段的起始if(dp[0][i-1] && dp[i][j-1] && dp[j][n-1])return true;return false;}
};
3.4 分割回文串II(hard)
🔗题目链接
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是回文。
返回符合要求的 最少分割次数 。
同样先预处理数据,方便判断子串是否是回文串;
剩下的分析方法与 1.4 单词拆分题 一样:
- dp[i] 表示 s[0, i] 位置上的最长字串的最小分割次数;
- 当分析 dp[i] 的时候,需要将[0, i] 分成两部分:
-
首先是离 i 最近的 [j, i],找到能满足是回文的 j,
-
再找 [0, j-1] 的最小分割次数,正是和状态表示一样,于是有
dp[i], [0, i] 是回文,0[0, i] 不是回文,有 0 < j <= i,[j, i] 是回文,求 min(dp[j]+1)[j, i] 不是回文,不考虑
-
🐎代码如下:
class Solution {
public:int minCut(string s) {int n = s.size();// 1. 预处理:子串是否是回文vector<vector<bool>> sub(n, vector<bool>(n));for(int i = n - 1; i >= 0; i--)for(int j = i; j < n; j++)if(s[i] == s[j])sub[i][j] = i+1 < j ? sub[i+1][j-1] : true;// 2. 分割,是另一个dp问题咯~vector<int> dp(n, 0x3f3f3f3f);for(int i = 0; i < n; i++){if(sub[0][i]) dp[i] = 0;elsefor(int j = 1; j <= i; j++)if(sub[j][i])dp[i] = min(dp[j - 1] + 1, dp[i]);}return dp[n-1];}
};
🥰如果本文对你有些帮助,欢迎👉 点赞 收藏 关注,你的支持是对作者大大莫大的鼓励!!(✿◡‿◡) 若有差错恳请留言指正~~
相关文章:

【算法】【动规】回文串系列问题
文章目录 跳转汇总链接3.1 回文子串3.2 最长回文子串3.3 分割回文串 IV3.4 分割回文串II(hard) 跳转汇总链接 👉🔗动态规划算法汇总链接 3.1 回文子串 🔗题目链接 给定一个字符串 s ,请计算这个字符串中有多少个回文子字符串。 …...

4-Docker命令之docker logs
1.docker logs介绍 docker logs命令是用来获取docker容器的日志 2.docker logs用法 docker logs [参数] CONTAINER [root@centos79 ~]# docker logs --helpUsage: docker logs [OPTIONS] CONTAINERFetch the logs of a containerAliases:docker container logs, docker lo…...

svelte基础语法学习
官网文档地址:绑定 / Each 块绑定 • Svelte 教程 | Svelte 中文网 1、样式 一般情况下父子组件内样式隔离、同级组件间样式隔离 2、页面布局 <style>P{color: red;} </stye><script> // 类似data let name ‘jiang’ let countVal 0 let s…...

Node.js教程-mysql模块
概述 在Node.js中,mysql模块是实现MySQL协议的JavaScript客户端工具。Node.js程序通过与MySQL建立链接,然后可对数据进行增、删、改、查等操作。 安装 由于mysql模块不是Node.js内置模块,需手动安装 npm i mysql注意:若MySQL服…...
网络通信协议
WebSocket通信 WebSocket是一种基于TCP的网络通信协议,提供了浏览器和服务器之间的全双工通信(full-duplex)能力。在WebSocket API中,浏览器和服务器只需要完成一次握手,两者之间就直接可以创建持久性的连接ÿ…...
Spark集群部署与架构
在大数据时代,处理海量数据需要分布式计算框架。Apache Spark作为一种强大的大数据处理工具,可以在集群中高效运行,处理数十TB甚至PB级别的数据。本文将介绍如何构建和管理Spark集群,以满足大规模数据处理的需求。 Spark集群架构…...
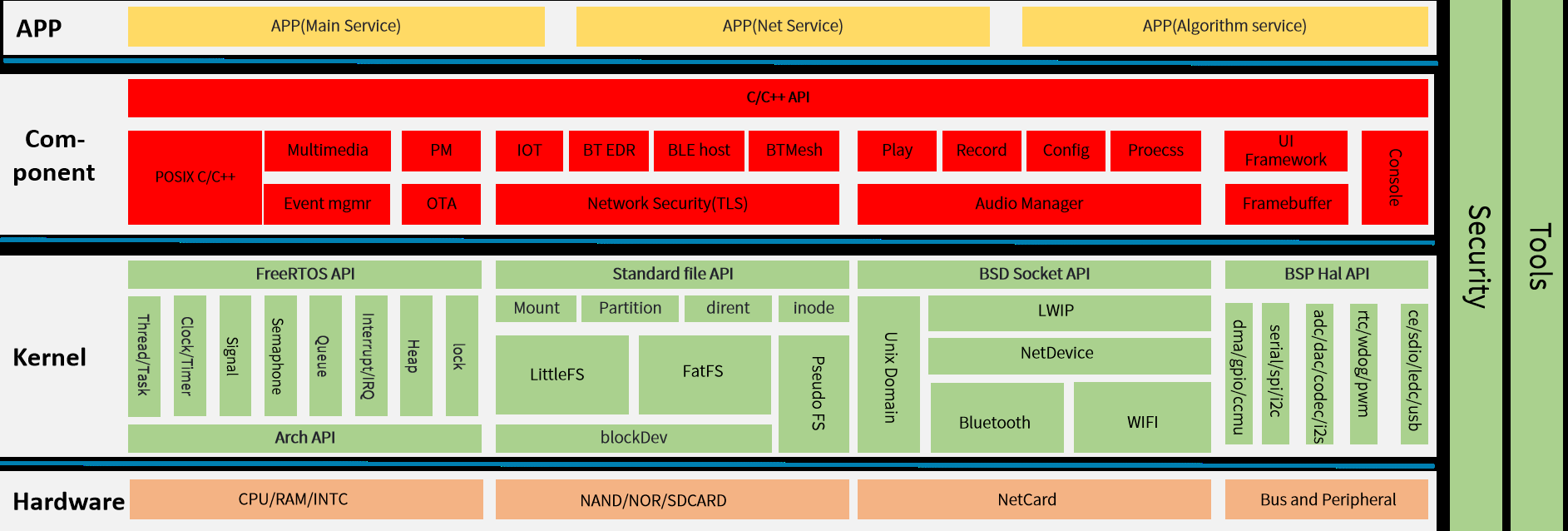
DshanMCU-R128s2 SDK 架构与目录结构
R128 S2 是全志提供的一款 M33(ARM)C906(RISCV-64)HIFI5(Xtensa) 三核异构 SoC,同时芯片内部 SIP 有 1M SRAM、8M LSPSRAM、8M HSPSRAM 以及 16M NORFLASH。 本文档作为 R128 FreeRTOS SDK 开发指南,旨在帮助软件开发工程师、技术支持工程师快速上手&am…...

【5G PHY】NR参考信号功率和小区总传输功率的计算
博主未授权任何人或组织机构转载博主任何原创文章,感谢各位对原创的支持! 博主链接 本人就职于国际知名终端厂商,负责modem芯片研发。 在5G早期负责终端数据业务层、核心网相关的开发工作,目前牵头6G算力网络技术标准研究。 博客…...

k8s学习 — 各知识点快捷入口
k8s学习 — 各知识点快捷入口 k8s学习 — 第一章 核心概念 k8s学习 — 第一章 核心概念 命名空间 实践: k8s学习 — (实践)第二章 搭建k8s集群k8s学习 — (实践)第三章 深入Podk8s学习 — (实践࿰…...

【Python】Python 批量转换PDF到Excel
PDF是面向展示和打印使用的,并未考虑编辑使用,所以缺少了很多编辑属性且非常难修改PDF里面的数据。当您需要分析或修改PDF文档数据时,可以将PDF保存为Excel工作簿,实现轻松编辑数据的需求。PDF转Excel,技术关键就是提取…...

Python并行计算和分布式任务全面指南
更多Python学习内容:ipengtao.com 大家好,我是彭涛,今天为大家分享 Python并行计算和分布式任务全面指南。全文2900字,阅读大约8分钟 并发编程是现代软件开发中不可或缺的一部分,它允许程序同时执行多个任务࿰…...

微信小程序promise封装
一. 在utils文件夹内创建一个request.js 写以下封装的 wx.request() 方法 const baseURL https:// 域名 ; //公用总路径地址 export const request (params) > { //暴露出去一个函数,并且接收一个外部传入的参数let dataObj params.data || {}; //…...

hash长度扩展攻击
作为一个信息安全的人,打各个学校的CTF比赛是比较重要的! 最近一个朋友发了道题目过来,发现有道题目比较有意思,这里跟大家分享下 这串代码的大致意思是: 这段代码首先引入了一个名为"flag.php"的文件&am…...
设计模式--命令模式
实验16:命令模式 本次实验属于模仿型实验,通过本次实验学生将掌握以下内容: 1、理解命令模式的动机,掌握该模式的结构; 2、能够利用命令模式解决实际问题。 [实验任务]:多次撤销和重复的命令模式 某系…...

单例模式的七种写法
为什么使用单例? 避免重复创建对象,节省内存,方便管理;一般我们在工具类中频繁使用单例模式; 1.饿汉式(静态常量)-[可用] /*** 饿汉式(静态常量)*/ public class Singleton1 {private static final Singleton1 INSTANCE new Singleton1();private Singleton1(){}…...
ElasticSearch入门介绍和实战
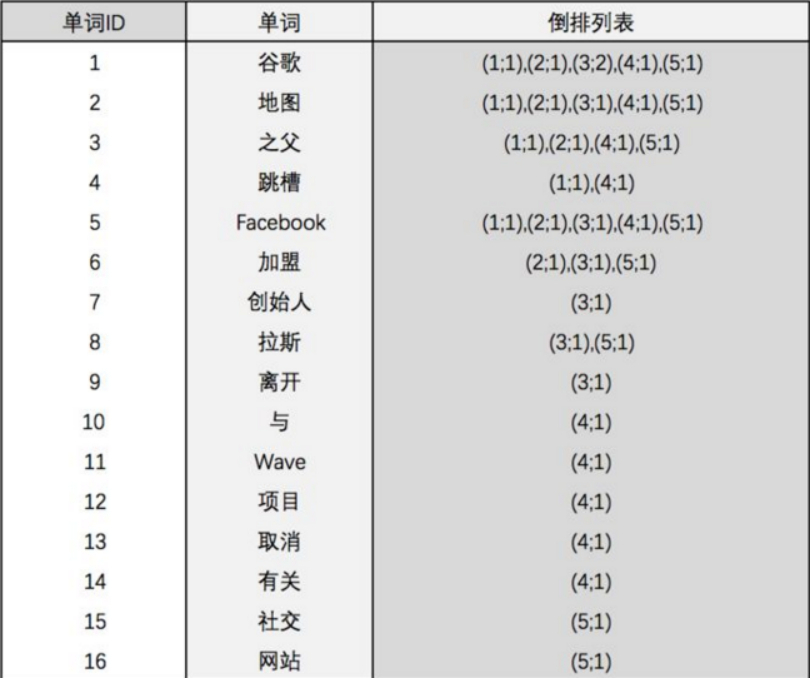
目录 1.ElasticSearch简介 1.1 ElasticSearch(简称ES) 1.2 ElasticSearch与Lucene的关系 1.3 哪些公司在使用Elasticsearch 1.4 ES vs Solr比较 1.4.1 ES vs Solr 检索速度 2. Lucene全文检索框架 2.1 什么是全文检索 2.2 分词原理之倒排索引…...

【FPGA】分享一些FPGA视频图像处理相关的书籍
在做FPGA工程师的这些年,买过好多书,也看过好多书,分享一下。 后续会慢慢的补充书评。 【FPGA】分享一些FPGA入门学习的书籍【FPGA】分享一些FPGA协同MATLAB开发的书籍 【FPGA】分享一些FPGA视频图像处理相关的书籍 【FPGA】分享一些FPGA高速…...
)
AUTOSAR从入门到精通-车载以太网(四)
目录 前言 原理 车载以太网发展历史 为何选择车载以太网...

MySQL报错:1054 - Unknown column ‘xx‘ in ‘field list的解决方法
我在操作MySQL遇到1054报错,报错内容:1054 - Unknown column Cindy in field list,下面演示解决方法,非常简单。 根据箭头指示,Cindy对应的应该是VARCHAR文本数字类型,字符串要用引号,所以解决方…...
:40+个依赖子模块之ActionBarShadow)
【Android 13】使用Android Studio调试系统应用之Settings移植(四):40+个依赖子模块之ActionBarShadow
文章目录 一、篇头二、系列文章2.1 Android 13 系列文章2.2 Android 9 系列文章2.3 Android 11 系列文章三、子模块AS移植3.1 AS创建目标3.2 创建ActionBarShadow(1)使用VS Code打开org_settings/SettingsLib目录(2)ActionBarShadow的Manifest.xml(3)ActionBarShadow的An…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...

DAY 45 超大力王爱学Python
来自超大力王的友情提示:在用tensordoard的时候一定一定要用绝对位置,例如:tensorboard --logdir"D:\代码\archive (1)\runs\cifar10_mlp_experiment_2" 不然读取不了数据 知识点回顾: tensorboard的发展历史和原理tens…...
