Simple Baselines for Image Restoration
Abstract.
尽管近年来在图像恢复领域取得了长足的进步,但SOTA方法的系统复杂性也在不断增加,这可能会阻碍对方法的分析和比较。在本文中,我们提出了一个简单的基线,超过了SOTA方法,是计算效率。为了进一步简化基线,我们揭示了非线性激活函数,如Sigmoid、ReLU、GELU、Softmax等是不必要的:它们可以用乘法替换或删除。因此,我们从基线推导出一个非线性激活自由网络,即NAFNet。SOTA结果在各种具有挑战性的基准上实现,例如在GoPro(用于图像去模糊)上达到33.69 dB PSNR,超过了以前的SOTA 0.38 dB,仅消耗了8.4%的计算成本;在SIDD(用于图像去噪)上,PSNR为40.30 dB,超过了以前的SOTA 0.28 dB,而计算成本不到原来的一半。代码和经过训练的模型可以在github.com/megvii-research/NAFNet上发布。
1 Introduction
随着深度学习技术的发展,图像恢复方法的性能有了明显的提高。基于深度学习的方法[5,37,39,36,6,7,32,8,25]取得了巨大的成功。例如,[39]和[8]在SIDD[1]/GoPro[26]上的PSNR分别达到40.02/33.31 dB,用于图像去噪/去模糊。
尽管这些方法具有良好的性能,但它们存在较高的系统复杂性。为了便于讨论,我们将系统复杂度分解为两个部分:块间复杂度和块内复杂度。首先是块间复杂度,如图2所示。[7,25]引入不同大小的特征图之间的联系;[5,37]是多阶段网络,后期对前一阶段的结果进行细化。二是块内复杂性,即块内的各种设计选择。例如[39]中的Multi-Dconv Head Transposed Attention Module和Gated Dconv前馈网络(如图3a所示),[22]中的Swin Transformer Block,[5]中的HINBlock,等等。逐一评估设计选择是不现实的。
基于上述事实,一个自然的问题出现了:低块间复杂度和低块内复杂度的网络是否可能实现SOTA性能?为了实现第一个条件(块间复杂度低),本文采用单级UNet作为体系结构(遵循了一些SOTA方法[39,36]),重点关注第二个条件。为此,我们从一个简单的块开始,其中包含最常见的组件,即卷积、ReLU和快捷方式[14]。从普通块开始,我们添加/替换SOTA方法的组件,并验证这些组件能带来多少性能增益。通过广泛的消融研究,我们提出了一个简单的基线,如图3c所示,它超过了SOTA方法,并且计算效率很高。它有可能激发新的想法,并使它们的验证更容易。由GELU[15]和通道注意模块[16](CA)组成的基线可以进一步简化:我们发现基线中的GELU可以被视为门控线性单元[10](GLU)的一个特例,并由此经验地证明它可以被一个简单的门取代,即特征映射的元素级积。此外,我们还揭示了CA与GLU在形式上的相似性,并且可以去除CA中的非线性激活函数。总之,简单的基线可以进一步简化为非线性无激活网络,即NAFNet。我们主要对SIDD[1]进行图像去噪,对GoPro[26]进行图像去模糊实验,如下[5,39,37]。主要结果如图1所示,我们提出的基线和NAFNet在实现SOTA结果的同时具有计算效率:在GoPro上33.40/33.69 dB,分别超过了之前的SOTA[8] 0.09/0.38 dB,计算成本为8.4%;超过[39].;28 dB,计算成本不到其一半。我们进行了大量的数量和质量实验,以说明我们提出的基线的有效性。
本文的主要贡献如下:
通过对SOTA方法进行分解并提取其基本组件,我们形成了一个系统复杂度较低的基线(见图3c),它可以超过之前的SOTA方法,并且具有较低的计算成本,如图1所示。它可以帮助研究人员激发新的想法,并方便地评估它们。
通过揭示GELU、Channel Attention to Gated Linear Unit之间的联系,我们通过删除或替换非线性激活函数(如Sigmoid、ReLU和GELU),进一步简化了基线,并提出了一个非线性激活自由网络,即NAFNet。虽然简化了,但它可以匹配或超过基线。据我们所知,这是首次证明非线性激活函数在SOTA计算机视觉方法中可能不需要。这项工作可能有潜力扩展SOTA计算机视觉方法的设计空间。
2 Related Works
2.1 Image Restoration
图像恢复任务的目的是将退化的图像(如噪声,模糊)恢复为一个干净的图像。最近,基于深度学习的方法[5,37,39,36,6,7,32,8,25]在这些任务上实现了SOTA结果,大多数方法可以被视为经典解UNet[29]的变体。它堆叠块到一个u形结构与跳跃连接。这些变体带来了性能的提高,以及系统的复杂性,我们将复杂性大致分为块间复杂度和块内复杂度。
块间复杂度[37,5]为多级网络,即后期对前一阶段的结果进行细化,每一阶段为u形结构。本设计基于将困难的图像恢复任务分解为多个子任务有助于提高性能的假设。不同的是,[7,25]采用了单阶段设计并获得了竞争性的结果,但它们引入了各种大小的特征图之间的复杂连接。有些方法同时采用了上述策略,如[32]。其他的SOTA方法,如[39,36]保持了单级UNet的简单结构,但它们引入了块内复杂性,我们将在下面讨论。
块内复杂性有很多不同的块内设计方案,我们在这里举几个例子。[39]通过通道注意图而不是空间注意图降低了自我注意[34]的记忆复杂度和时间复杂度。前馈网络采用门控线性单元[10]和深度卷积。[36]引入了基于windows的多头自我注意,类似于[22]。此外,在其块中引入局部增强前馈网络,在前馈网络中加入深度卷积,增强局部信息捕获能力。不同的是,我们揭示了增加系统复杂性并不是提高性能的唯一方法:SOTA性能可以通过一个简单的基线实现。
2.2 Gated Linear Units
门控线性单元[10](GLU)可以通过两个线性变换层的逐元生成来解释,其中一个线性变换层被非线性激活。GLU或其变体已经在NLP中验证了其有效性[30,10,9],并且在计算机视觉中有很好的发展趋势[32,39,17,20]。在本文中,我们揭示了GLU带来的非平凡的改进。与[30]不同的是,我们在不降低GLU性能的情况下,去掉了GLU中的非线性激活函数。此外,基于非线性激活自由GLU本身包含非线性(由于两次线性变换的乘积会产生非线性)的事实,我们的基线可以通过用两个特征映射的乘法替换非线性激活函数来简化。据我们所知,这是第一个在没有非线性激活函数的情况下实现SOTA性能的计算机视觉模型。
相关文章:

Simple Baselines for Image Restoration
Abstract.尽管近年来在图像恢复领域取得了长足的进步,但SOTA方法的系统复杂性也在不断增加,这可能会阻碍对方法的分析和比较。在本文中,我们提出了一个简单的基线,超过了SOTA方法,是计算效率。为了进一步简化基线&…...
)
Python数据可视化:局部整体图表可视化(基础篇—6)
目录 1、饼图 2、圆环图 3、马赛克图 4、华夫饼图 5、块状/点状柱形图 在学习本篇博文之前请先看一看之前发过的关联知识:...
CSDN新星计划新玩法、年度勋章挑战赛开启
文章目录🌟 写在前面🌟 逐步亮相的活动🌟 勋章挑战赛🌟 新星计划🌟 有付费课程才可参与?🌟 成就铭牌🌟 博客跟社区的关系🌟 写在最后🌟 写在前面 哈喽&#…...
Docker之部署Mysql
通过docker对Mysql进行部署。 如果没有部署过docker,看我之前写的目录拉取镜像运行容器开放端口拉取镜像 前往dockerHub官网地址,搜索mysql。 找到要拉取的镜像版本,在tag下找到版本。 拉取mysql镜像,不指定版本数,…...
基于C/C++获取电脑网卡的IP地址信息
目录 前言 一、网卡是什么? 二、实现访问网卡信息 1.引入库及相关的头文件 2.操作网卡数据 3. 完整代码实现 4.结果验证 总结 前言 简单示例如何在windows下使用c/c代码实现 ipconfig/all 指令 提示:以下是本篇文章正文内容,下面案例可供参考…...

28相似矩阵和若尔当标准型
一、关于正定矩阵的一些补充 在此之前,先讲一下对称矩阵中那些特征值为正数的矩阵,这样特殊的矩阵称为正定矩阵。其更加学术的定义是: SSS 是一个正定矩阵,如果对于每一个非零向量xxx,xTSx>0x^TSx>0xTSx>0 正…...

springboot操作MongoDB
启动类及配置import com.mongodb.client.MongoClient;import com.mongodb.client.MongoClients;import com.mongodb.client.internal.MongoClientImpl;import org.springframework.boot.SpringApplication;import org.springframework.boot.autoconfigure.SpringBootApplicatio…...
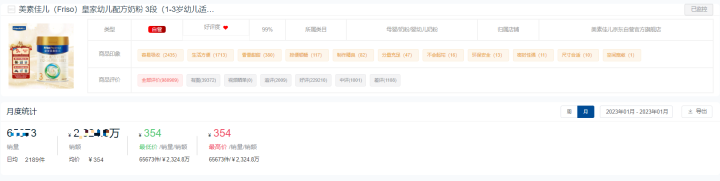
1月奶粉电商销售数据榜单:销售额约20亿,高端化趋势明显
鲸参谋电商数据监测的2023年1月份京东平台“奶粉”品类销售数据榜单出炉! 根据鲸参谋数据显示,1月份京东平台上奶粉的销量约675万件,销售额约20亿元,环比均下降19%左右。与去年相比,整体也下滑了近34%。可以看出&#…...
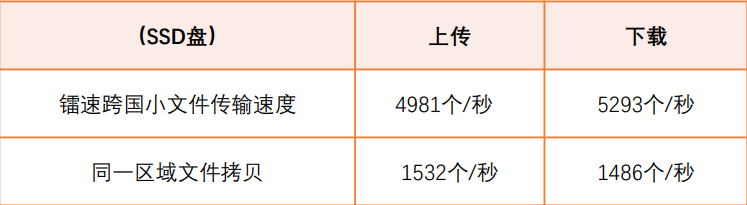
跨境数据传输是日常业务中经常且至关重要的组成部分
跨境数据传输是日常业务中经常且至关重要的组成部分。在过去的20年中,由于全球通信网络和业务流程的发展,全球数据流的模式已迅速发展。随着数据从数据中心移到数据中心和/或跨边界移动,安全漏洞已成为切实的风险。有可能违反国家和国际数据传…...

错误: tensorflow.python.framework.errors_impl.OutOfRangeError的解决方案
近日,在使用CascadeRCNN完成目标检测任务时,我在使用这个模型训练自己的数据集时出现了如下错误: tensorflow.python.framework.errors_impl.OutOfRangeError: PaddingFIFOQueue _1_get_batch/batch/padding_fifo_queue is closed and has in…...

springboot项目初始化执行sql
Sprint Boot应用可以在启动的时候自动执行项目根路径下的SQL脚本文件。我们需要先将sql脚本写好,并将这些静态资源都放置在src/main/resources文件夹下。 再配置application.yml: spring.datasource.initialization-mode 必须配置初始化模式initializa…...

Kubernetes之存储管理(中)
NFS网络存储 emptyDir和hostPath存储,都仅仅是把数据存储在pod所在的节点上,并没有同步到其他节点,如果pod出现问题,通过deployment会产生一个新的pod,如果新的pod不在之前的节点,则会出现问题,…...
MySQL workbench的基本操作
1. 创建新的连接 hostname主机名输入“local host”和“127.0.0.1”效果是一样的,指的是本地的服务器。 需要注意的是,此处的密码在安装软件的时候已经设定。 点击【Test Connection】,测试连接是否成功。 创建完的连接可以通过,…...

【Flink】FlinkSQL中Table和DataStream互转
在我们实际使用Flink的时候会面临很多复杂的需求,很可能需要FlinkSQL和DataStream互相转换的情况,这就需要我们熟练掌握Table和DataStream互转,本篇博客给出详细代码以及执行结果,可直接使用,通过例子可学会Table和DataStream互转,具体步骤如下: maven如下<?xml ver…...
一)
网络总结知识点(网络工程师必备)一
♥️作者:小刘在C站 ♥️个人主页:小刘主页 ♥️每天分享云计算网络运维课堂笔记,努力不一定有收获,但一定会有收获加油!一起努力,共赴美好人生! ♥️夕阳下,是最美的绽放,树高千尺,落叶归根人生不易,人间真情 目录 1.TCP UDP协议的区别 2.ARP是第几层协议,其作用...
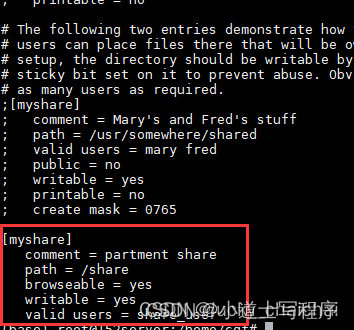
离线安装samba与配置(.tar方式安装)
一、samba离线安装【安装并设置成功后,相关文件及其位置:①smbd:/usr/local/samba/sbin/smbd②nmdb:/usr/local/samba/sbin/nmbd③配置文件 smb.conf:/usr/local/samba/lib/smb.conf④添加用户的 smbpasswd 文件&#…...
[Java基础]—JDBC
前言 其实学Mybatis前就该学了,但是寻思目前主流框架都是用mybatis和mybatis-plus就没再去看,结果在代码审计中遇到了很多cms是使用jdbc的因此还是再学一下吧。 第一个JDBC程序 sql文件 INSERT INTO users(id, NAME, PASSWORD, email, birthday) VAL…...
基本面向对象编程-计算机基本功能实现_
《C/S项目实训》实验报告 实验名称: 基本面向对象编程-计算机基本功能实现_ 一、实验目的 通过综合实践项目,理解Java 程序设计是如何体现面向对象编程基本思想,掌握OOP方法,掌握事件触发、消息响应机制。进一步巩固面向对…...

C++面向对象之多态性
文章目录C面向对象之多态性1.静态多态2.动态多态3.多态的好处3.1使用方法4.纯虚函数5.虚析构与纯虚析构5.1问题5.2解决6.其他知识点7.代码8.测试结果8.1父类中无虚函数,父类的指针指向子类对象,将调用父类中的函数,无法调用子类中的重写函数&…...

Android性能优化系列篇:弱网优化
弱网优化1、Serializable原理通常我们使用Java的序列化与反序列化时,只需要将类实现Serializable接口即可,剩下的事情就交给了jdk。今天我们就来探究一下,Java序列化是怎么实现的,然后探讨一下几个常见的集合类,他们是…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...
