当前位置： 首页 > news >正文

Crow：Middlewares 庖丁解牛7 after_handlers_call_helper

news 2026/2/3 20:52:15

Crow：Middlewares 庖丁解牛6 middleware_call_helper-CSDN博客

介绍了对插件before_handle的调用

当完成了detail::middleware_call_helper的调用后，如果没有在before_handle中设置req被终止处理，也就是

if (!res.completed_)
{need_to_call_after_handlers_ = true;handler_->handle(req_, res, routing_handle_result_);
}

handler_->handle(req_, res, routing_handle_result_);

也就是Crow：http请求到Rule绑定的handler_的调用链-CSDN博客

说明的通过handl

相关文章：

Crow：Middlewares 庖丁解牛7 after_handlers_call_helper

Crow：Middlewares 庖丁解牛6 middleware_call_helper-CSDN博客 介绍了对插件before_handle的调用 当完成了detail::middleware_call_helper的调用后，如果没有在before_handle中设置req被终止处理，也就是 if (!res.completed_) {need_to_call_after_handlers_ = true;handler…...

编程日记 2023/12/25 22:44:52

ts相关笔记（extends、infer、Pick、Omit）

最近刷了本ts小册，对一些知识点做下笔记。 extends extends 是一个关键字，用于对类型参数做一些约束。 A extends B 意味着 A 是 B 的子类型，比如下面是成立的 ‘abc’ extends string599 extends number 看下面例子： type …...

编程日记 2023/12/25 22:41:49

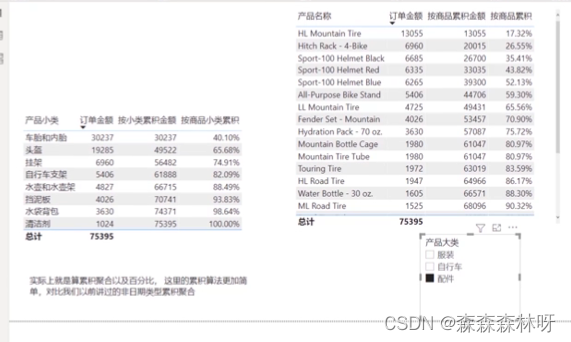
8.21 PowerBI系列之DAX函数专题-帕累托分析

需求 实现 1 按商品小类累积 var rollup_sales calculate(//计算当前累计销售额 [销售额], filter(allselected(order_2[产品小类]),sum(order_2[订单金额])<[销售额]) ) //按小类累积金额,filter内的销售额为选中的各小类的销售额 //金额从大到小累积&#xff0c;用&l…...

编程日记 2023/12/25 22:40:49

结构体-2-测试排名

22-结构体-2-测试排名 [命题人 : 外部导入] 时间限制 : 1.000 sec 内存限制 : 128 MB 题目描述 为了提升同学们的编程能力&#xff0c;老师们会在平时进行C语言的上机测试&#xff0c;了解班上同学的学习情况&#xff0c;对于一些测试成绩较差的同学&#xff0c;老师会进行督促…...

编程日记 2023/12/25 22:38:47

LeetCode刷题---快乐数

解题思路 该题的解题思路为使用哈希表来存储每次平方的和的结果&#xff0c;看是否有重复的数&#xff0c;如果存在第n次的平方和的数和第i次(i<n)平方和的数想等&#xff0c;那么它就不是一个快乐数。否则&#xff0c;则为快乐数。 代码实现&#xff1a; public boolean i…...

编程日记 2023/12/25 22:33:42

web前端游戏项目-辨色大比拼【附源码】

web前端游戏项目-辨色大比拼【附源码】 《辨色大比拼》是一个旨在测试和提升玩家颜色识别能力的在线游戏。在游戏中&#xff0c;玩家将通过辨识颜色来解谜并推进游戏进程。辨色大比拼也是一个寓教于乐的游戏&#xff0c;它不仅提供了一个有趣的辨色挑战&#xff0c;还能帮助玩…...

编程日记 2023/12/25 22:32:41

MongoDB操作_数据库_集合

.......................................................................................................................................................... 三、MongoDB操作 3.1 数据库操作 一个mongodb中可以建立多个数据库。 MongoDB的默认数据库为"test…...

编程日记 2023/12/25 22:30:39

50个免费的 AI 工具，提升工作效率（附网址）

上次我们已经介绍了20个精选的提高工作效率的免费AI工具&#xff0c;但如果你觉得这些AI工具还不过瘾的话&#xff0c;想进一步成为职场中最了解AI的人&#xff0c;本文将汇总介绍免费最新的50个AI工具。 DeepSwap DeepSwap 是一个基于 AI 的工具&#xff0c;适用于想要制作令人…...

编程日记 2023/12/25 22:29:38

g++ strip debug

strip(1) command_--strip-debug-CSDN博客 strip main.outll main.out -rwxr-xr-x 1 root root 6272 Mar 22 16:14 main.outfile main.out main.out: ELF 64-bit LSB executable, x86-64, version 1 (SYSV), dynamically linked (uses shared libs), for GNU/Linux 2.6.32, Bu…...

编程日记 2023/12/25 22:28:37

微服务实战系列之Dubbo（上）

前言 随着一年一度冬至的到来&#xff0c;2023的步伐也将远去。而博主的系列文章&#xff0c;也将从今天起&#xff0c;越来越聚焦如何构建微服务“内核”上。前序系列文章几乎囊括了微服务的方方面面&#xff0c;无论使用什么框架、组件或工具&#xff0c;皆可拿来用之。 那么…...

编程日记 2023/12/25 22:27:36

一篇讲透：箭头函数、普通函数有什么区别

前言 &#x1f4eb; 大家好&#xff0c;我是南木元元&#xff0c;热衷分享有趣实用的文章&#xff0c;希望大家多多支持&#xff0c;一起进步&#xff01; &#x1f345; 个人主页&#xff1a;南木元元 目录 什么是箭头函数 箭头函数和普通函数的区别 更简洁的语法 箭头函数…...

编程日记 2023/12/25 22:21:30

第40节: Vue3 注册生命周期钩子

在UniApp中使用Vue3框架时&#xff0c;你可以注册生命周期钩子来执行特定的逻辑。以下是一个示例&#xff0c;演示了如何在UniApp中使用Vue3框架注册生命周期钩子&#xff1a; <template> <view> <p>{{ message }}</p> </view> </templ…...

编程日记 2023/12/25 22:20:30

docker给容器分配固定ip

1.为 Docker 容器设置一个固定的 IP 地址 要为 Docker 容器设置一个固定的 IP 地址&#xff0c;有几种常见的方法&#xff1a; 使用自定义网络和静态 IP 地址&#xff1a; 你可以创建一个自定义的 Docker 网络&#xff0c;并在这个网络上为容器分配静态 IP 地址。首先&#x…...

编程日记 2023/12/25 22:19:29

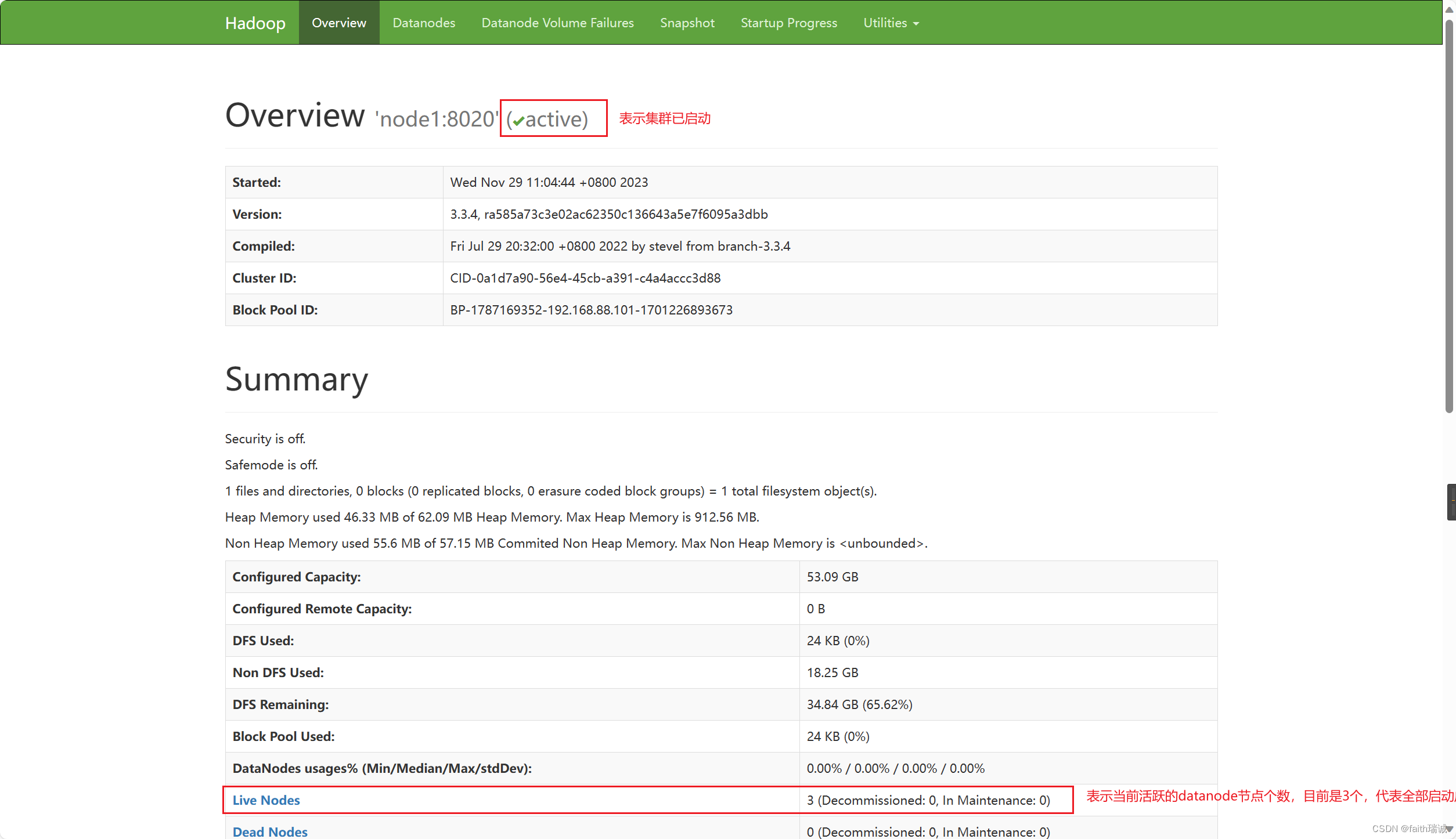
Hadoop入门学习笔记——二、在虚拟机里部署HDFS集群

视频课程地址&#xff1a;https://www.bilibili.com/video/BV1WY4y197g7 课程资料链接&#xff1a;https://pan.baidu.com/s/15KpnWeKpvExpKmOC8xjmtQ?pwd5ay8 Hadoop入门学习笔记&#xff08;汇总&#xff09; 目录 二、在虚拟机里部署HDFS集群2.1. 部署node1虚拟机2.2. 部…...

编程日记 2023/12/25 22:18:28

Spring之国际化：i18n

学习的最大理由是想摆脱平庸&#xff0c;早一天就多一份人生的精彩&#xff1b;迟一天就多一天平庸的困扰。各位小伙伴&#xff0c;如果您&#xff1a; 想系统/深入学习某技术知识点… 一个人摸索学习很难坚持&#xff0c;想组团高效学习… 想写博客但无从下手&#xff0c;急需…...

编程日记 2023/12/25 22:17:27

Java读取类路径下的JSON文件并转换为实体列表

使用 Jackson 库来读取类路径下的 JSON 文件并将其转换为对应实体列表。 在实际开发中可能在本地环境中需要调用别人的接口&#xff0c;别人的接口如果还没开发好或者本地环境不支持外部接口调用的时候&#xff0c;可以读取json文件来造数据&#xff0c;方便调试。 以Student…...

编程日记 2023/12/25 22:15:24

复分析——第1章——复分析准备知识(E.M. Stein R. Shakarchi)

第一章 复分析准备知识 (Preliminaries to Complex Analysis) The sweeping development of mathematics during the last two centuries is due in large part to the introduction of complex numbers; paradoxically, this is based on the seemingly absurd no…...

编程日记 2023/12/25 22:12:20

C++ 继承方式

C++ 继承方式 实验介绍 本章节将学习权限关键字的使用，并将一一举例验证 public、protected、private 的使用，学完本小节实验后将彻底掌握权限关键字的使用。 知识点 权限关键字使用位置继承中的权限关键字public 继承protected 继承private 继承权限关键字使用位置 示例…...

编程日记 2023/12/25 22:03:13

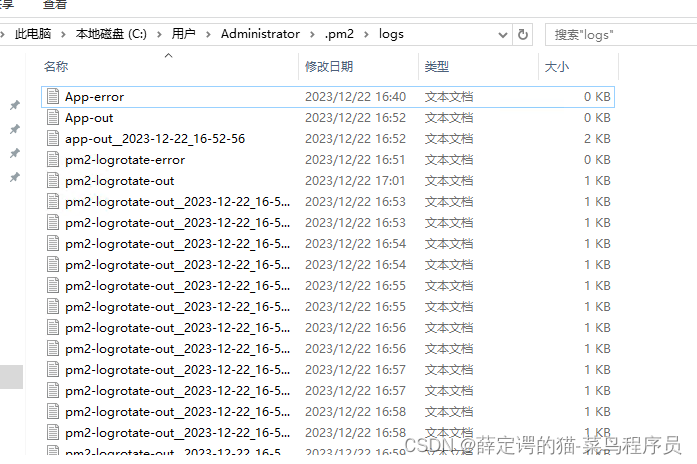
华为云Windows Server服务器下，Node使用pm2-logrotate分割pm2日志，解决pm2日志内存占用过高的问题。

一、简介 PM2 是一个守护进程管理器&#xff0c;它将帮助您管理和保持您的应用程序在线。PM2 入门很简单&#xff0c;它以简单直观的 CLI 形式提供&#xff0c;可通过 NPM 安装。官网地址&#xff1a;https://pm2.keymetrics.io/ 二、问题&#xff1a;pm2日志内存占用过高&am…...

编程日记 2023/12/25 22:01:11

web3风险投资公司之Electric Capital

文章目录 什么是 Electric CapitalElectric团队 Electric Capital 开发者报告参考 什么是 Electric Capital 官网&#xff1a;https://www.electriccapital.com/ 官方github&#xff1a;https://github.com/electric-capital Electric Capital 是一家投资于加密货币、区块链企…...

编程日记 2023/12/25 22:00:10

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)

题目&#xff1a;3442. 奇偶频次间的最大差值 I 思路 &#xff1a;哈希&#xff0c;时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况&#xff0c;哈希表这里用数组即可实现。 C版本&#xff1a; class Solution { public:int maxDifference(string s) {int a[26]…...

编程新知 2026/2/2 22:26:49

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析

一、变量声明设计&#xff1a;let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性&#xff0c;这种设计体现了语言的核心哲学。以下是深度解析&#xff1a; 1.1 设计理念剖析 安全优先原则&#xff1a;默认不可变强制开发者明确声明意图 let x 5; …...

编程新知 2025/9/28 20:12:12

web vue 项目 Docker化部署

Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段&#xff1a; 构建阶段&#xff08;Build Stage&#xff09;&#xff1a…...

编程新知 2025/8/12 16:28:43

conda相比python好处

Conda 作为 Python 的环境和包管理工具&#xff0c;相比原生 Python 生态&#xff08;如 pip 虚拟环境&#xff09;有许多独特优势&#xff0c;尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处&#xff1a; 一、一站式环境管理&#xff1a…...

编程新知 2025/11/29 6:54:19

设计模式和设计原则回顾

设计模式和设计原则回顾 23种设计模式是设计原则的完美体现，设计原则设计原则是设计模式的理论基石， 设计模式 在经典的设计模式分类中（如《设计模式：可复用面向对象软件的基础》一书中），总共有23种设计模式，分为三大类： 一、创建型模式（5种） 1. 单例模式（Sing…...

编程新知 2025/12/14 20:57:41

【Oracle APEX开发小技巧12】

有如下需求&#xff1a; 有一个问题反馈页面&#xff0c;要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据&#xff0c;方便管理员及时处理反馈。 我的方法&#xff1a;直接将逻辑写在SQL中&#xff0c;这样可以直接在页面展示 完整代码&#xff1a; SELECTSF.FE…...

编程新知 2026/1/31 12:19:33

Qt Http Server模块功能及架构

Qt Http Server 是 Qt 6.0 中引入的一个新模块&#xff0c;它提供了一个轻量级的 HTTP 服务器实现&#xff0c;主要用于构建基于 HTTP 的应用程序和服务。 功能介绍&#xff1a; 主要功能 HTTP服务器功能&#xff1a; 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

编程新知 2025/10/17 21:16:57

Java 加密常用的各种算法及其选择

在数字化时代&#xff0c;数据安全至关重要&#xff0c;Java 作为广泛应用的编程语言&#xff0c;提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景&#xff0c;有助于开发者在不同的业务需求中做出正确的选择。​ 一、对称加密算法…...

编程新知 2025/11/22 20:41:02

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分

一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计&#xff0c;提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合&#xff1a;各模块职责清晰&#xff0c;便于独立开发…...

编程新知 2025/10/13 4:15:41

Map相关知识

数据结构 二叉树 二叉树&#xff0c;顾名思义&#xff0c;每个节点最多有两个“叉”&#xff0c;也就是两个子节点&#xff0c;分别是左子 节点和右子节点。不过&#xff0c;二叉树并不要求每个节点都有两个子节点&#xff0c;有的节点只 有左子节点&#xff0c;有的节点只有…...

编程新知 2026/1/26 21:25:32