用 C 语言开发一门编程语言 — 函数库的设计与实现
目录
文章目录
- 目录
- 前言
- 前文列表
- 基础功能演示
- 数字运算
- 变量与代数运算
- 列表处理
- Lambda 函数
- 条件分支
- 字符串
- 源文件加载
- 函数库
- 列表处理函数库
- 条件分支函数库
- 数学库
前言
通过开发一门类 Lisp 的编程语言来理解编程语言的设计思想,本实践来自著名的《Build Your Own Lisp》。
- 代码实现:https://github.com/JmilkFan/Lispy
前文列表
《用 C 语言开发一门编程语言 — 交互式解析器》
《用 C 语言开发一门编程语言 — 语法解析器运行原理》
《用 C 语言开发一门编程语言 — 波兰表达式解析器》
《用 C 语言开发一门编程语言 — 表达式存储器》
《用 C 语言开发一门编程语言 — 符号表达式解析器》
《用 C 语言开发一门编程语言 — 引用表达式解析器》
《用 C 语言开发一门编程语言 — 变量的设计与实现》
《用 C 语言开发一门编程语言 — 基于 Lambda 表达式的函数设计与实现》
《用 C 语言开发一门编程语言 — 条件分支的设计与实现》
《用 C 语言开发一门编程语言 — 字符串的设计与实现》
基础功能演示
目前为止,我们开发的编程语言已经拥有了以下功能:
- 交互式解析器界面;
- MPC 语法解析器;
- 基于波兰表达式的数字运算;
- 基于符号表达式的代数运算;
- 基于引用表达式的变量;
- 基于 Lambda 表达式的函数;
- 条件分支逻辑控制语句;
- 文件加载;
- 等等。
在本文中,我们将完整的演示上述技术功能,并尝试通过预定义一些常用的函数库来辅助编程。
数字运算
lispy> + 4 5 // 4+5
9
lispy> - 8 3 // 8-3
5
lispy> * 6 2 // 6 * 2
12
lispy> / 10 5 // 10/5
2
lispy> / 10 0 // 10/0
Division By Zero!
lispy> - (* 10 10) (+ 1 1 1) // (10*10) - (1+1+1)
97
变量与代数运算
lispy> def {x} 1
()
lispy> + x 1
2
lispy> def {y} 2
()
lispy> + x y
3
lispy> def {a b} 2 3
()
lispy> + a b
5
lispy> + x (* a b) y // x + (a * b) + y
9
lispy> def {arglist} {a b c d}
()
lispy> def arglist 1 2 3 4
()
lispy> list a b c d
{1 2 3 4}
列表处理
lispy> def { l1 } {1 2 3}
()
lispy> def { l2 } {4 5 6}
()
lispy> head l1
{1}
lispy> tail l1
{2 3}
lispy> join l1 l2
{1 2 3 4 5 6}
lispy> list l1 l1
{{1 2 3} {1 2 3}}
lispy> eval {+ 1 2 3}
6
Lambda 函数
lispy> def {add-mul} (\ {x y} {+ x (* x y)})
()
lispy> add-mul 10 20
210
lispy> add-mul 30 40
1230
lispy> def {add-mul-ten} (add-mul 10)
()
lispy> add-mul-ten 50
510
条件分支
lispy> def {x y} 100 200
()
lispy> if (== x y) {+ x y} {- x y}
-100
lispy> if (< x y) {+ x y} {- x y}
300
字符串
lispy> print "Hello World!"
"Hello World!"
()
lispy> error "This is an error!"
This is an error!
源文件加载
$ cat hello.lspy
(print "hello world.")$ main hello.lspy
"hello world."
函数库
列表处理函数库
- list.lspylib
; 空类型
(def {nil} {}); 布尔类型
(def {true} 1)
(def {false} 0); 函数定义 Lambda 表达式
(def {fun} (\ {f b} {def (head f) (\ (tail f) b)
})); 取列表中的第一、二、三项
(fun {fst l} { eval (head l) })
(fun {snd l} { eval (head (tail l)) })
(fun {trd l} { eval (head (tail (tail l))) }); 获取列表长度
(fun {len l} {if (== l nil){0}{+ 1 (len (tail l))}
}); 取列表中的第 n 项
(fun {nth n l} {if (== n 0){fst l}{nth (- n 1) (tail l)}
}); 取列表中的最后一项
(fun {last l} {nth (- (len l) 1) l}); 取列表中的前 n 项
(fun {take n l} {if (== n 0){nil}{join (head l) (take (- n 1) (tail l))}
}); 删除列表中的前 n 项
(fun {drop n l} {if (== n 0){l}{drop (- n 1) (tail l)}
}); 从第 n 项分裂列表
(fun {split n l} {list (take n l) (drop n l)}); 取元素的 idx
(fun {elem x l} {if (== l nil){false}{if (== x (fst l)) {true} {elem x (tail l)}}
}); Map 函数:所有列表元素执行相同的操作
(fun {map f l} {if (== l nil){nil}{join (list (f (fst l))) (map f (tail l))}
}); Filter 函数:根据过滤条件进行元素过滤
(fun {filter f l} {if (== l nil){nil}{join (if (f (fst l)) {head l} {nil}) (filter f (tail l))}
}); Fold Left 函数:向左折叠逐一执行指定函数操作
(fun {foldl f z l} {if (== l nil){z}{foldl f (f z (fst l)) (tail l)}
}); 向左折叠求和
(fun {sum l} {foldl + 0 l})
; 向左折叠求积
(fun {product l} {foldl * 1 l})
应用:列表处理。
lispy> load "./samples/list.lspylib"
()
lispy> def {l1} {1 2 3 4 5 6}
()
lispy> len l1
6
lispy> nth 2 l1
3
lispy> last l1
6
lispy> take 3 l1
{1 2 3}
lispy> def {l2} (drop 4 l1)
()
lispy> l2
{5 6}
lispy> split 5 l1
{{1 2 3 4 5} {6}}
lispy> elem 1 l1
1
lispy> elem 7 l1
0
lispy> map (\ {x} {+ x 10}) {5 2 11} // 所有元素的数值 +10
{15 12 21}
lispy> filter (\ {x} {> x 2}) {5 2 11 -7 8 1} // 过滤出 >2 的元素
{5 11 8}
lispy> sum l1 // 求和
21
lispy> product l1 // 求积
720
条件分支函数库
- condition.lspylib
; 空类型
(def {nil} {}); 布尔类型
(def {true} 1)
(def {false} 0); 函数定义 Lambda 表达式
(def {fun} (\ {f b} {def (head f) (\ (tail f) b)
})); 取列表中的第一、二、三项
(fun {fst l} { eval (head l) })
(fun {snd l} { eval (head (tail l)) })
(fun {trd l} { eval (head (tail (tail l))) }); Unpack List for Function
(fun {unpack f l} {eval (join (list f) l)
})
; Pack List for Function
(fun {pack f & xs} {f xs}); switch 关键字
(fun {switch & cs} {if (== cs nil){error "No Selection Found"}{if (fst (fst cs)) {snd (fst cs)} {unpack switch (tail cs)}}
}); default 关键字
(def {default} true); case 关键字
(fun {case x & cs} {if (== cs nil){error "No Case Found"}{if (== x (fst (fst cs))) {snd (fst cs)} {unpack case (join (list x) (tail cs))}}
}); 条件选择月份后缀函数
(fun {month-day-suffix i} {switch{(== i 0) "st"}{(== i 1) "nd"}{(== i 3) "rd"}{default "th"}
}); 条件选择星期几函数
(fun {day-name x} {case x{0 "Monday"}{1 "Tuesday"}{2 "Wednesday"}{3 "Thursday"}{4 "Friday"}{5 "Saturday"}{6 "Sunday"}
})
- 应用:switch/case 语句。
lispy> load "./samples/condition.lspylib"
()
lispy> month-day-suffix 1
"nd"
lispy> month-day-suffix 2
"th"
lispy> day-name 0
"Monday"
lispy> day-name 1
"Tuesday"
数学库
- fibonacci.lspylib
; 空类型
(def {nil} {}); 布尔类型
(def {true} 1)
(def {false} 0); 函数定义 Lambda 表达式
(def {fun} (\ {f b} {def (head f) (\ (tail f) b)
})); 取列表中的第一、二、三项
(fun {fst l} { eval (head l) })
(fun {snd l} { eval (head (tail l)) })
(fun {trd l} { eval (head (tail (tail l))) }); Unpack List for Function
(fun {unpack f l} {eval (join (list f) l)
})
; Pack List for Function
(fun {pack f & xs} {f xs}); switch 关键字
(fun {switch & cs} {if (== cs nil){error "No Selection Found"}{if (fst (fst cs)) {snd (fst cs)} {unpack switch (tail cs)}}
}); default 关键字
(def {default} true); Fibonacci
(fun {fib n} {switch{ (== n 0) 0 }{ (== n 1) 1 }{ default (+ (fib (- n 1)) (fib (- n 2))) }
})
- 应用:
lispy> load "./samples/fibonacci.lspylib"
()
lispy>
()
lispy> fib 10
55
lispy> fib 20
6765
相关文章:

用 C 语言开发一门编程语言 — 函数库的设计与实现
目录 文章目录目录前言前文列表基础功能演示数字运算变量与代数运算列表处理Lambda 函数条件分支字符串源文件加载函数库列表处理函数库条件分支函数库数学库前言 通过开发一门类 Lisp 的编程语言来理解编程语言的设计思想,本实践来自著名的《Build Your Own Lisp》…...
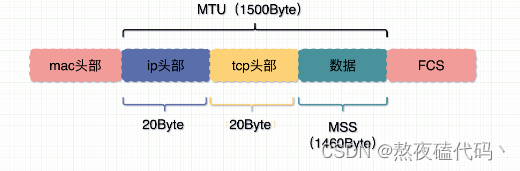
网络层IP协议与数据链路层以太网协议
文章目录一、IP协议IP地址地址管理路由选择DNS二、以太网协议以太网帧MTU一、IP协议 IP协议是我们网络层的代表协议,今天我们就来一起学习一下吧,我们这里介绍的主要是IPv4协议。 版本:指定IP协议的版本,版本的取值只有4&#x…...
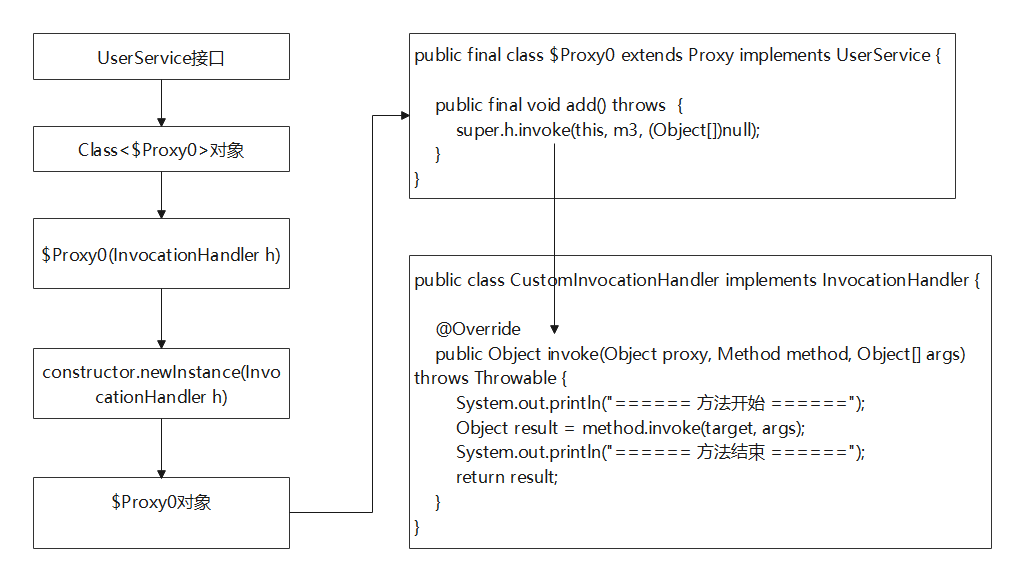
JDK动态代理详解
1.什么是动态代理 可能很多小伙伴首次接触动态代理这个名词的时候,或者是在面试过程中被问到动态代理的时候,不能很好的描述出来,动态代理到底是个什么高大上的技术。不方,其实动态代理的使用非常广泛,例如我们平常使用…...

实时的软件生成 —— Prompt 编程打通低代码的最后一公里?
PS:这也是一篇畅想,虽然经过了一番试验,依旧有一些不足,但是大体上站得住脚。传统的软件生成方式需要程序员编写大量的代码,然后进行测试、发布等一系列繁琐的流程。而实时生成技术则是借助人工智能技术,让…...
互联网工程师 1480 道 Java 面试题及答案整理 ( 2023 年 整理版)
最近很多粉丝朋友私信我说:熬过了去年的寒冬却没熬过现在的内卷;打开 Boss 直拒一排已读不回,回的基本都是外包,薪资还给的不高,对技术水平要求也远超从前;感觉 Java 一个初中级岗位有上千人同时竞争&#…...

Spark开发
第一步:创建RDD Spark提供三种创建RDD方式:** 集合、本地文件、HDFS文件** 使用程序中的集合创建RDD,主要用于进行测试,可以在实际部署到集群运行之前,自己使用集合构造一些测试数据,来测试后面的spark应…...

Tornado异步框架
简介: tornado是Python的web框架。tornado和主流的web服务器框架有明显的区别:它是非阻塞式服务器,而且速度非常快,得力于其非阻塞的方式和epoll的运用tornado可以每秒处理数以千计的连接(号称) 基本配置 …...

openpnp - error - 吸嘴没下降到板子上, 就将元件松开
文章目录openpnp - error - 吸嘴没下降到板子上, 就将元件松开概述笔记ENDopenpnp - error - 吸嘴没下降到板子上, 就将元件松开 概述 以前用过国内一家openpnp厂家出的设备, 他们家的openpnp是自己改过的. 贴片流程已经走过一遍. 这次还是按照以前记录的笔记, 按照国内那家的…...

【Java】yyyy-MM-dd HH:mm:ss 时间格式 时间戳 全面解读超详细
时间格式 时间格式(协议)描述gg时期或纪元。y不包含纪元的年份。不具有前导零。yy不包含纪元的年份。具有前导零。yyyy包含纪元的四位数的年份。M月份数字。一位数的月份没有前导零。MM月份数字。一位数的月份有一个前导零。MMM月份的缩写名称,在AbbreviatedMonthN…...

快鲸SCRM发布口腔企业私域运营解决方案
口腔企业普遍面临着以下几方面运营痛点问题 1、获客成本居高不下,恶性竞争严重 2、管理系统落后,人员流失严重 3、客户顾虑多、决策时间长 4、老客户易流失,粘性差 以上这些痛点,不得不倒逼口腔企业向精细化运营客户迈进。 …...
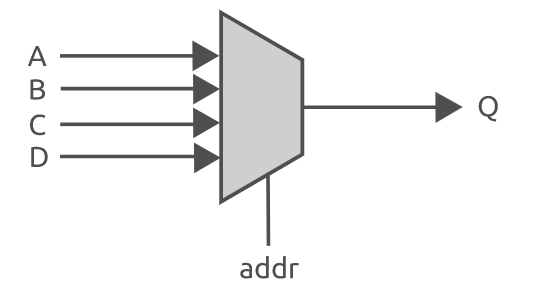
Verilog实现组合逻辑电路
在verilog 中可以实现的数字电路主要分为两类----组合逻辑电路和时序逻辑电路。组合逻辑电路比较简单,仅由基本逻辑门组成---如与门、或门和非门等。当电路的输入发生变化时,输出几乎(信号在电路中传递时会有一小段延迟)立即就发生…...

2023前端菜鸟笔试血泪史html5-one--找到工作前都更新
1.说说对html语义化的理解 什么的HTML语义化,顾名思义,HTML语义化就是可以不通过了解HTML的内容,就可以知道这个部分所代表的的意义。 HTML语义化的意义:在使用HTML标签构建页面时,避免大篇幅的使用无语义的标签。 …...
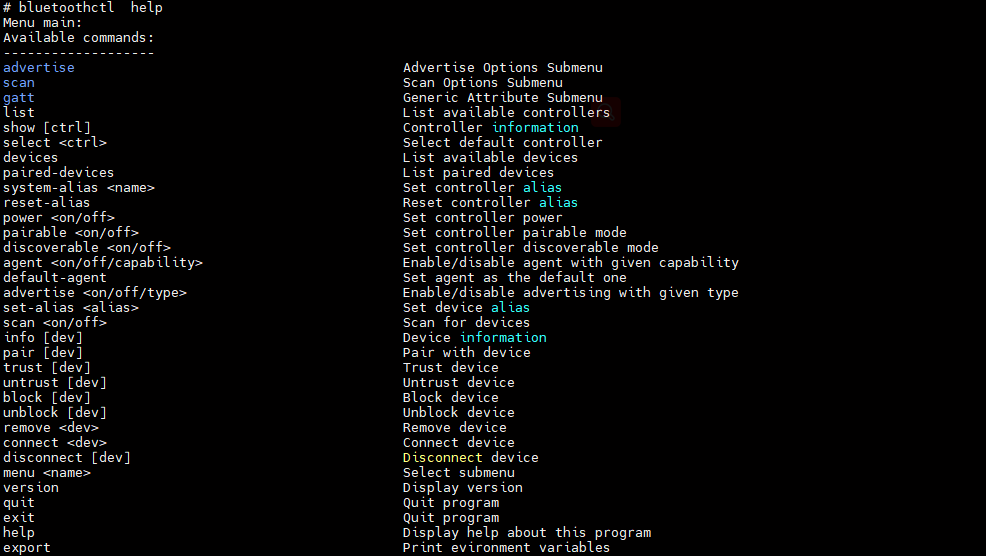
蓝牙调试工具集合汇总
BLE 该部分主要分享一下常用的蓝牙调试工具,方便后续蓝牙抓包及分析。 目录 1 hciconfig 2 hcitool 3 hcidump 4 hciattach 5 btmon 6 bluetoothd 7 bluetoothctl 1 hciconfig 工具介绍:hciconfig,HCI 设备配置工具 命令格式&…...

Java 获取文件后缀名【一文总结所有方法】
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...
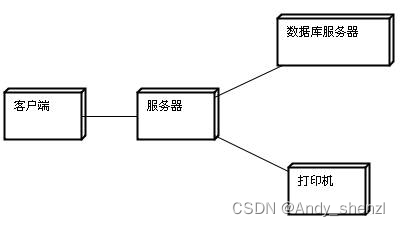
UML常见图的总结
一、概述 UML:Unified Modeling Language,统一建模语言,支持从需求分析开始的软件开发的全过程。是一个支持模型化和软件系统开发的图形化语言、为软件开发的所有阶段提供模型化和可视化支持,包括由需求分析到规格,到…...

WebRTC系列-工具系列之音频相关工具
文章目录 1. audio_util数据格式转换类2. WavFile文件读写类2.1 读取wav文件2.2 写入wav文件这篇文章主要介绍WebRTC中一些音频工具这些,大部分都在 common_audio目录下,这个文件夹下提供音频的大量算法,包括sinc重采样算法,音频数据格式的转换:例如 float转int16_t格式等…...
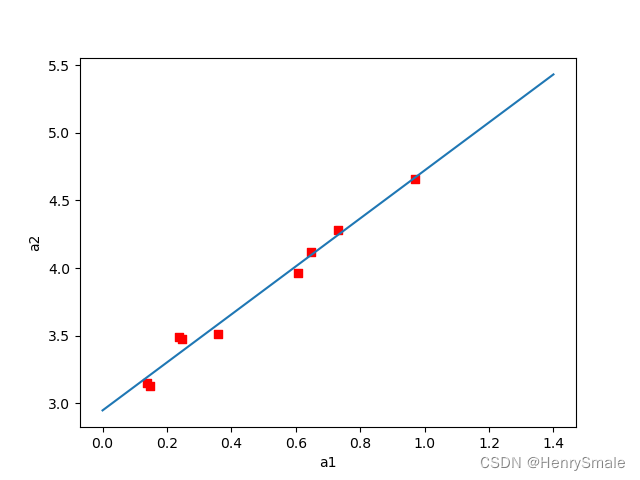
7 线性回归及Python实现
1 统计指标 随机变量XXX的理论平均值称为期望: μE(X)\mu E(X)μE(X)但现实中通常不知道μ\muμ, 因此使用已知样本来获取均值 X‾1n∑i1nXi.\overline{X} \frac{1}{n} \sum_{i 1}^n X_i. Xn1i1∑nXi.方差variance定义为: σ2E(∣X−μ∣2).\sigma^2 E(|…...

适合小团队协作、任务管理、计划和进度跟踪的项目任务管理工具有哪些?
适合小团队协作、任务管理、计划和进度跟踪的项目任务管理工具有哪些? 大家可以参考这个模板:http://s.fanruan.com/irhj8管理项目归根结底在管理人、物,扩展来说便是: 人:员工能力、组织机制; 物:项目内…...

从100%进口到自主可控,从600块降到10块,中科院攻克重要芯片
前言 2月28日,“20多位中科院专家把芯片价格打到10块”冲上微博热搜,据河南省官媒大象新闻报道,热搜中提到的中科院专家所在企业为全球最大的PLC分路器芯片制造商仕佳光子,坐落于河南鹤壁。 为实现芯片技术自主可控自立自强&#…...

关于git的一些基本点总结
1.什么是git? git是一个常用的分布式版本管理工具。 2.git 的常用命令: clone(克隆): 从远程仓库中克隆代码到本地仓库 checkout (检出):从本地仓库中检出一个仓库分支然后进行修订 add(添加): 在提交前…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...
