7 线性回归及Python实现
1 统计指标
- 随机变量XXX的理论平均值称为期望: μ=E(X)\mu = E(X)μ=E(X)
- 但现实中通常不知道μ\muμ, 因此使用已知样本来获取均值
X‾=1n∑i=1nXi.\overline{X} = \frac{1}{n} \sum_{i = 1}^n X_i. X=n1i=1∑nXi. - 方差variance定义为:
σ2=E(∣X−μ∣2).\sigma^2 = E(|X - \mu|^2). σ2=E(∣X−μ∣2). - 用已知样本的数据来代替:
S2=Var(X)=1n∑i=1n(Xi−μ)2.S^2 = Var(X) = \frac{1}{n} \sum_{i = 1}^n (X_i - \mu)^2. S2=Var(X)=n1i=1∑n(Xi−μ)2. - 由于μ\muμ未知, 使用贝塞尔校正:
S2=Var(X)=1n−1∑i=1n(Xi−X‾)2.S^2 = Var(X) = \frac{1}{n - 1} \sum_{i = 1}^{n} (X_i - \overline{X})^2. S2=Var(X)=n−11i=1∑n(Xi−X)2. - 原因: 在已知数据上, 使用X‾\overline{X}X获得的结果一般更小:
∑i=1n−1(Xi−X‾)2≤∑i=1n−1(Xi−μ)2.\sum_{i = 1}^{n - 1} (X_i - \overline{X})^2 \leq \sum_{i = 1}^{n - 1} (X_i - \mu)^2. i=1∑n−1(Xi−X)2≤i=1∑n−1(Xi−μ)2. - 更多解释: https://www.zhihu.com/question/20099757
- 标准差:
σX=S=Var(X).\sigma_X = S = \sqrt{Var(X)}. σX=S=Var(X).
偏差与方差:
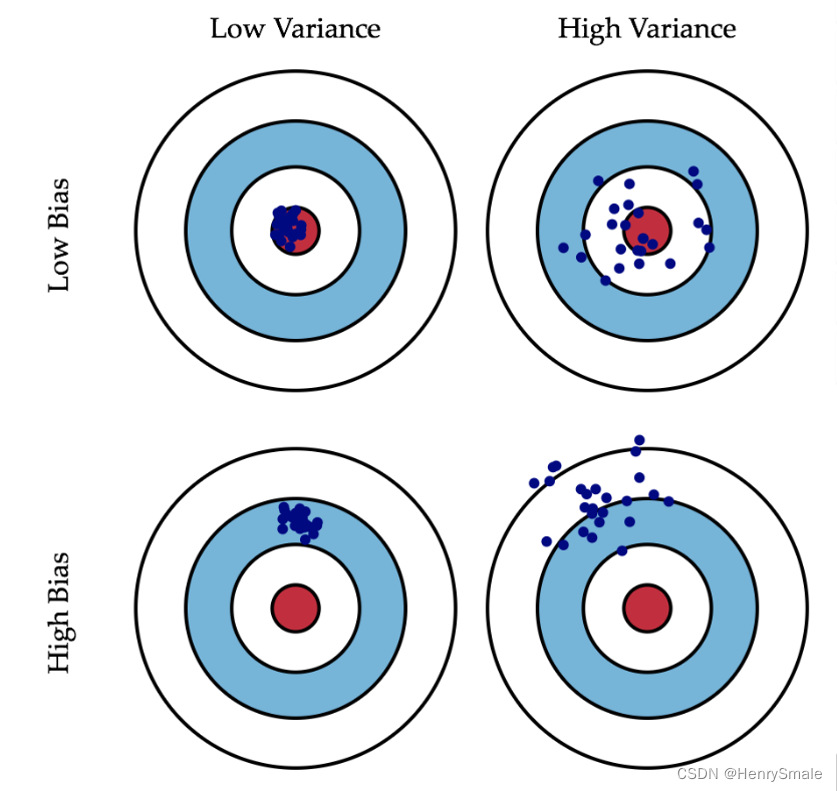
- 方差(again)
Var(X)=σX2=1n−1∑i=1n(Xi−X‾)(Xi−X‾).Var(X) = \sigma_X^2 = \frac{1}{n - 1} \sum_{i = 1}^{n} (X_i - \overline{X})(X_i - \overline{X}). Var(X)=σX2=n−11i=1∑n(Xi−X)(Xi−X). - 协方差
Cov(X,Y)=1n−1∑i=1n(Xi−X‾)(Yi−Y‾).Cov(X, Y) = \frac{1}{n - 1} \sum_{i = 1}^{n} (X_i - \overline{X})(Y_i - \overline{Y}). Cov(X,Y)=n−11i=1∑n(Xi−X)(Yi−Y). - Pearson相关系数
Corr(X,Y)=ρX,Y=Cov(X,Y)σXσY.Corr(X, Y) = \rho_{X, Y} = \frac{Cov(X, Y)}{\sigma_X \sigma_Y}. Corr(X,Y)=ρX,Y=σXσYCov(X,Y).
2 线性回归
2.1 回归任务
分类与回归
- 分类任务预测类别,即是/否等离散值:如是否生病;
- 回归任务预测实型值:如气温
拟合空间中的点 (注意数据点没有类别标记, 输出也占一维):
- 一个条件属性:直线;
- 两个条件属性:平面;
- 更多条件属性:超平面.
拟合线:
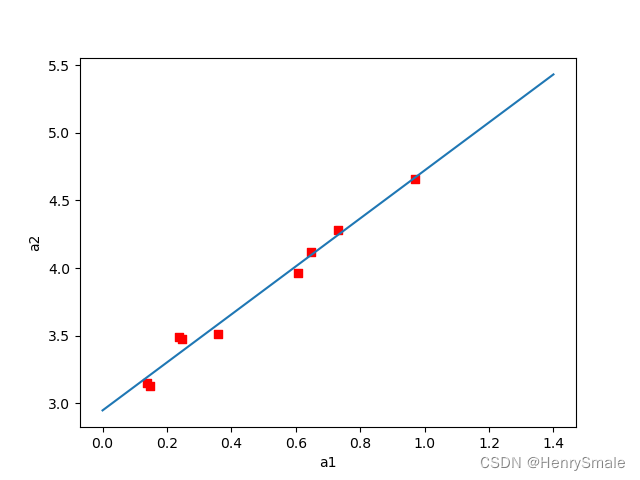
3 局部线性回归
4 岭回归
5 Lasso回归
6 小结
相关文章:

7 线性回归及Python实现
1 统计指标 随机变量XXX的理论平均值称为期望: μE(X)\mu E(X)μE(X)但现实中通常不知道μ\muμ, 因此使用已知样本来获取均值 X‾1n∑i1nXi.\overline{X} \frac{1}{n} \sum_{i 1}^n X_i. Xn1i1∑nXi.方差variance定义为: σ2E(∣X−μ∣2).\sigma^2 E(|…...

适合小团队协作、任务管理、计划和进度跟踪的项目任务管理工具有哪些?
适合小团队协作、任务管理、计划和进度跟踪的项目任务管理工具有哪些? 大家可以参考这个模板:http://s.fanruan.com/irhj8管理项目归根结底在管理人、物,扩展来说便是: 人:员工能力、组织机制; 物:项目内…...

从100%进口到自主可控,从600块降到10块,中科院攻克重要芯片
前言 2月28日,“20多位中科院专家把芯片价格打到10块”冲上微博热搜,据河南省官媒大象新闻报道,热搜中提到的中科院专家所在企业为全球最大的PLC分路器芯片制造商仕佳光子,坐落于河南鹤壁。 为实现芯片技术自主可控自立自强&#…...

关于git的一些基本点总结
1.什么是git? git是一个常用的分布式版本管理工具。 2.git 的常用命令: clone(克隆): 从远程仓库中克隆代码到本地仓库 checkout (检出):从本地仓库中检出一个仓库分支然后进行修订 add(添加): 在提交前…...
PyTorch保姆级安装教程
1 安装CUDA1.1 查找Nvidia适用的CUDA版本桌面右键,【打开 NVIDIA控制面板】查看【系统信息】查看NVIDIA的支持的CUDA的版本,下图可知支持的版本是 10.11.2 下载CUDACUDA下载官方网址https://developer.nvidia.com/cuda-toolkit-archive找到适合的版本下载…...
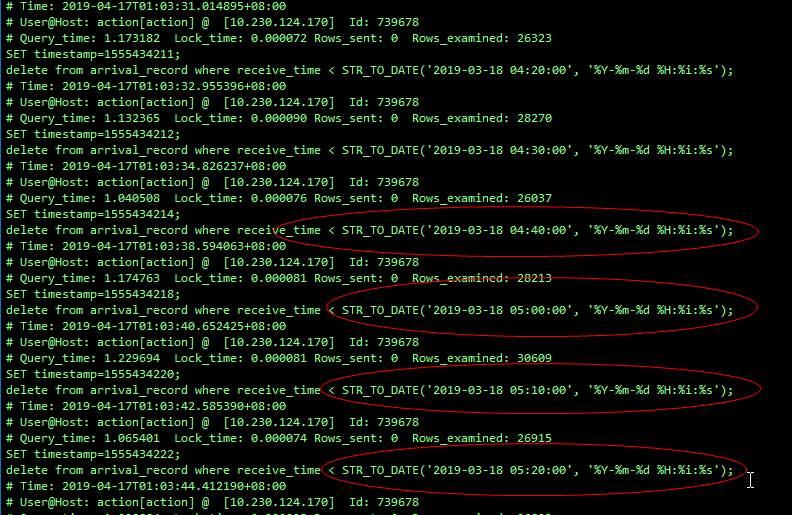
MySQL 上亿大表如何优化?
背景XX 实例(一主一从)xxx 告警中每天凌晨在报 SLA 报警,该报警的意思是存在一定的主从延迟。(若在此时发生主从切换,需要长时间才可以完成切换,要追延迟来保证主从数据的一致性)XX 实例的慢查询…...
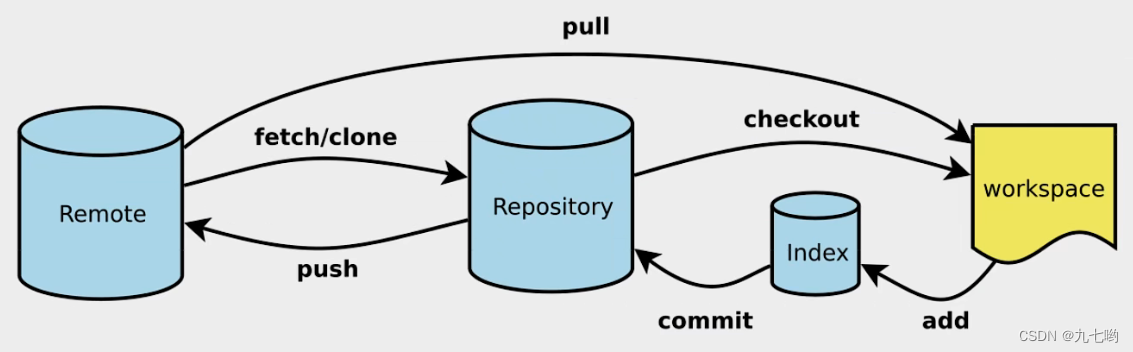
Git(狂神课堂笔记)
1.首先去git官网下载我们对应的版本Git - Downloading Package (git-scm.com) 2.安装后我们会发现git文件夹里有三个应用程序: Git Bash:Unix与Linux风格的命令行,使用最多,推荐最多 Git CMD:Windows风格的命令行 G…...

「2」指针进阶,最详细指针和数组难题解题思路
🐶博主主页:ᰔᩚ. 一怀明月ꦿ ❤️🔥专栏系列:线性代数,C初学者入门训练 🔥座右铭:“不要等到什么都没有了,才下定决心去做” 🚀🚀🚀大家觉不错…...

云服务器是做什么的?云服务器典型的应用场景介绍
云服务器可能是很多企业以及个人上云用户的必选产品了,但是对于初学者或者非专业的用户来说云服务器还是比较陌生的,它到底是干什么的,如此生活中哪些地方可以接触到,这篇文章将详细的介绍云服务器使用的应用场景以及相关的操作 本…...
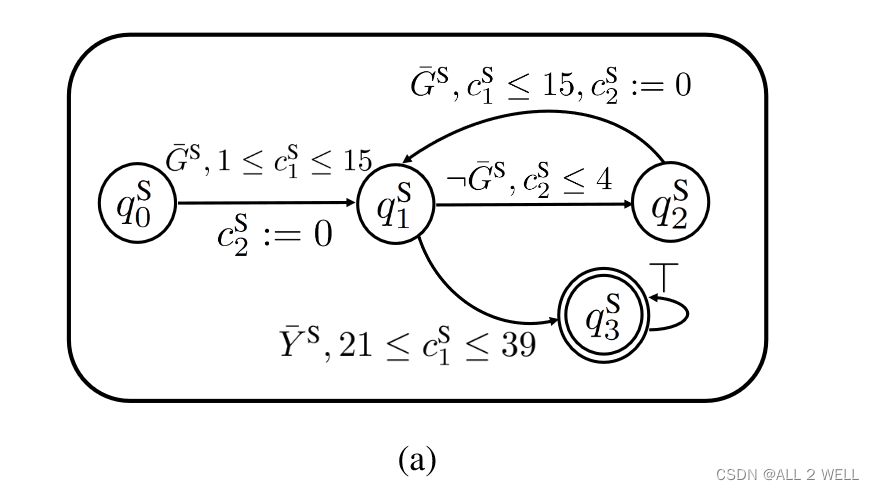
【论文随笔】Transfer of temporal logic formulas in reinforcement learning
Zhe Xu and Ufuk Topcu. 2019. Transfer of temporal logic formulas in reinforcement learning. In Proceedings of the 28th International Joint Conference on Artificial Intelligence (IJCAI’19). AAAI Press, 4010–4018. 这是一篇将inference和learning结合起来的文章…...

蓝桥杯-货物摆放
蓝桥杯-货物摆放1、题目描述1.1 答案提交1.2 运行限制2、解决方案2.1 方案一:暴力解法(三重循环)2.2 方案二:找出乘机的因子1、题目描述 小蓝有一个超大的仓库,可以摆放很多货物。 现在,小蓝有 n 箱货物要摆放在仓库,每…...

10 种顶流聚类算法 Python 实现(附完整代码)
聚类或聚类分析是无监督学习问题。它通常被用作数据分析技术,用于发现数据中的有趣模式,例如基于其行为的客户群。 有许多聚类算法可供选择,对于所有情况,没有单一的最佳聚类算法。相反,最好探索一系列聚类算法以及每…...

微信小程序第一节 —— 自定义顶部、底部导航栏以及获取胶囊体位置信息。
一、前言 大家好!我是 是江迪呀。我们在进行微信小程序开发时,常常需要自定义一些东西,比如自定义顶部导航、自定义底部导航等等。那么知道这些自定义内容的具体位置、以及如何适配不同的机型就变得尤为重要。下面让我以在iPhone机型&#x…...
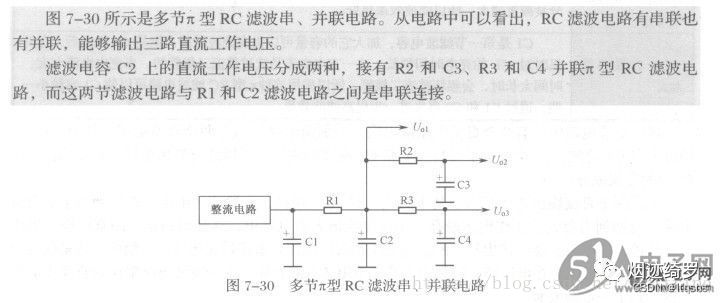
快速吃透π型滤波电路-LC-RC滤波器
π型滤波器简介 π型滤波器包括两个电容器和一个电感器,它的输入和输出都呈低阻抗。π型滤波有RC和LC两种, 在输出电流不大的情况下用RC,R的取值不能太大,一般几个至几十欧姆,其优点是成本低。其缺点是电阻要消耗一些…...
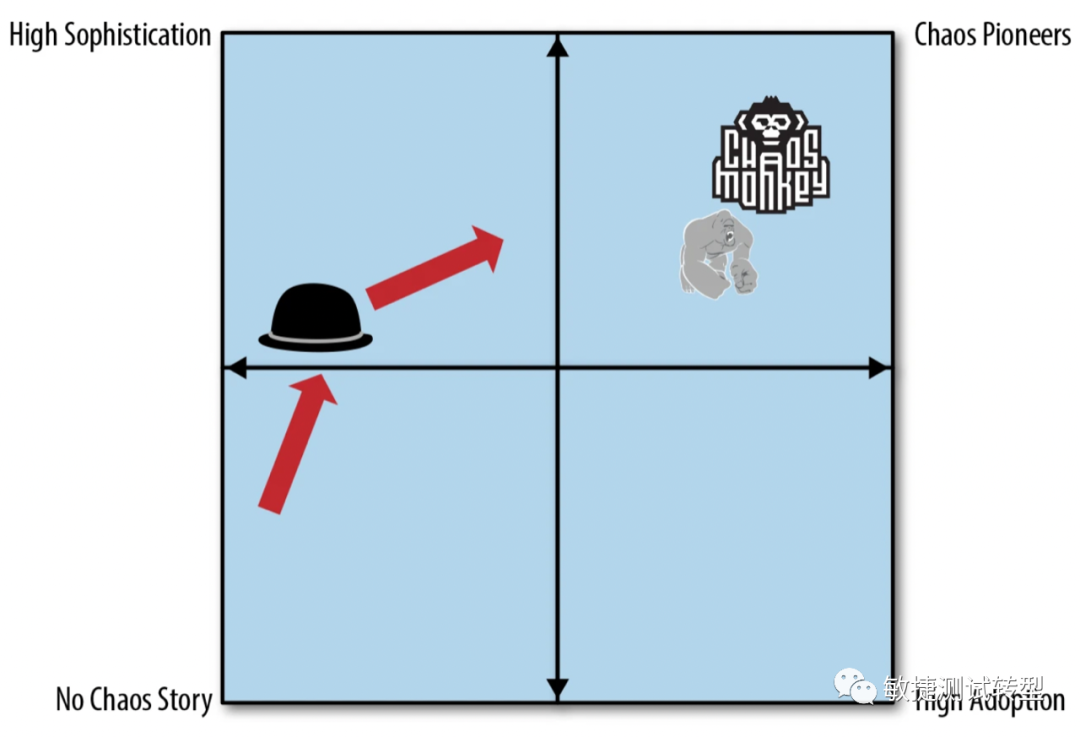
聊聊混沌工程
这是鼎叔的第五十四篇原创文章。行业大牛和刚毕业的小白,都可以进来聊聊。欢迎关注本专栏和微信公众号《敏捷测试转型》,大量原创思考文章陆续推出。混沌工程是一门新兴学科,它不仅仅只是个技术活动,还包含如何设计能够持续协作的…...

做为骨干网络的分类模型的预训代码安装配置简单记录
一、安装配置环境 1、准备工作 代码地址 GitHub - bubbliiiing/classification-pytorch: 这是各个主干网络分类模型的源码,可以用于训练自己的分类模型。 # 创建环境 conda create -n ptorch1_2_0 python3.6 # 然后启动 conda install pytorch1.2.0 torchvision…...

网络协议(九):应用层(域名、DNS、DHCP)
网络协议系列文章 网络协议(一):基本概念、计算机之间的连接方式 网络协议(二):MAC地址、IP地址、子网掩码、子网和超网 网络协议(三):路由器原理及数据包传输过程 网络协议(四):网络分类、ISP、上网方式、公网私网、NAT 网络…...
有趣的小知识(三)提升网站速度的秘诀:掌握缓存基础,让你的网站秒开
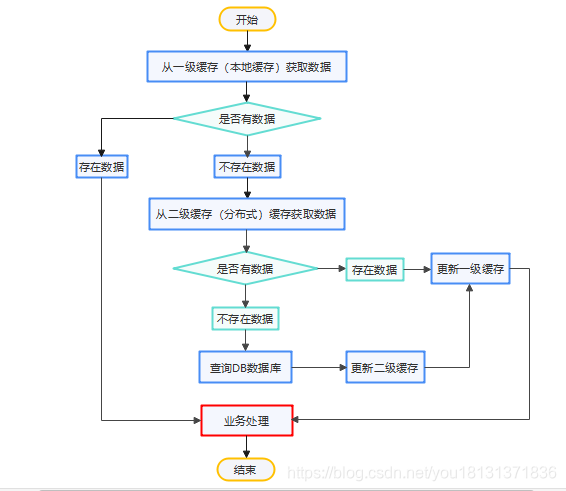
像MySql等传统的关系型数据库已经不能适用于所有的业务场景,比如电商系统的秒杀场景,APP首页的访问流量高峰场景,很容易造成关系型数据库的瘫痪,随着缓存技术的出现很好的解决了这个问题。 一、缓存的概念(什么是缓存…...

SpringCloud之服务拆分和实现远程调用案例
服务拆分对单体架构项目来说:简单方便,高度耦合,扩展性差,适合小型项目。而对于分布式架构来说:低耦合,扩展性好,但架构复杂,难度大。微服务就是一种良好的分布式架构方案࿱…...
: com.atguigu.dao.UserDao.save)
mybatis: Invalid bound statement (not found): com.atguigu.dao.UserDao.save
问题描述: 1 问题实质: dao层(又叫mapper接口)跟mapper.xml文件没有映射 2 问题原因: 出现这种映射问题的原因分为低级原因和更低级原因两种 更低级原因: (1)dao层的方法和mapper.xml中的方法不一样; (2)mapper中的namespace 值 和对应的dao层entity层不一致 &…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...

算法250609 高精度
加法 #include<stdio.h> #include<iostream> #include<string.h> #include<math.h> #include<algorithm> using namespace std; char input1[205]; char input2[205]; int main(){while(scanf("%s%s",input1,input2)!EOF){int a[205]…...

Qt的学习(二)
1. 创建Hello Word 两种方式,实现helloworld: 1.通过图形化的方式,在界面上创建出一个控件,显示helloworld 2.通过纯代码的方式,通过编写代码,在界面上创建控件, 显示hello world; …...

当下AI智能硬件方案浅谈
背景: 现在大模型出来以后,打破了常规的机械式的对话,人机对话变得更聪明一点。 对话用到的技术主要是实时音视频,简称为RTC。下游硬件厂商一般都不会去自己开发音视频技术,开发自己的大模型。商用方案多见为字节、百…...
