xgboost:算法数学原理
xgboost算法数学原理
1、求预测值
y^i=ϕ(xi)=∑k=1Kfk(xi),fk∈F,(1)\hat{y}_i=\phi\left(\mathbf{x}_i\right)=\sum_{k=1}^K f_k\left(\mathbf{x}_i\right), \quad f_k \in \mathcal{F},\tag{1} y^i=ϕ(xi)=k=1∑Kfk(xi),fk∈F,(1)
F={f(x)=wq(x)}(q:Rm→T,w∈RT)\mathcal{F}=\left\{f(\mathbf{x})=w_{q(\mathbf{x})}\right\}\left(q: \mathbb{R}^m \rightarrow T, w \in \mathbb{R}^T\right)F={f(x)=wq(x)}(q:Rm→T,w∈RT):递归树的的空间;
qqq:每棵树的结构,映射一个样本到一个叶子节点index;
T:T:T:叶子的数目;fkf_kfk对于一个独立的树结构qqq和叶子权重www。
wiw_iwi:在i−thi-thi−th叶子节点的分数;(与决策树不同,递归树在每个叶子节点上包含一个连续分数)。
示例图:(注:图中的人指的是一个个样本)
结合上面的公式理解就是对于样本iii的预测值等于KKK棵递归树样本落在的叶子节点对应的分数的和;

2、计算带正则项的损失
L(ϕ)=∑il(y^i,yi)+∑kΩ(fk)where Ω(f)=γT+12λ∥w∥2(2)\begin{aligned} & \mathcal{L}(\phi)=\sum_i l\left(\hat{y}_i, y_i\right)+\sum_k \Omega\left(f_k\right) \\ & \text { where } \Omega(f)=\gamma T+\frac{1}{2} \lambda\|w\|^2 \end{aligned}\tag{2} L(ϕ)=i∑l(y^i,yi)+k∑Ω(fk) where Ω(f)=γT+21λ∥w∥2(2)
lll:衡量预测值yi^\hat{y_i}yi^和目标值yiy_iyi差别的可微的凸函数;
Ω\OmegaΩ:模型复杂度的惩罚项;用于平滑最终的学习权重避免过拟合。正则化的目标函数倾向于选择一个更简单、可预测的函数(递归树模型);传统的梯度提升树没有用正则化项,RGF用到。
3、梯度树集成(Gradient Tree Boosting)
从对全部递归树的损失,利用贪心和近似,推导到一棵树的损失
为什么用(3)式作为目标函数而不是(2)式?
将(1)和(2)合并:
L(ϕ)=∑il(∑k=1Kfk(xi),yi)+∑kΩ(fk)where Ω(f)=γT+12λ∥w∥2(2)\begin{aligned} & \mathcal{L}(\phi)=\sum_i l\left(\sum_{k=1}^K f_k\left(\mathbf{x}_i\right), y_i\right)+\sum_k \Omega\left(f_k\right) \\ & \text { where } \Omega(f)=\gamma T+\frac{1}{2} \lambda\|w\|^2 \end{aligned}\tag{2} L(ϕ)=i∑l(k=1∑Kfk(xi),yi)+k∑Ω(fk) where Ω(f)=γT+21λ∥w∥2(2)
可以看到(2)式不能进行优化,不能优化的原因是KKK棵树的话,就有KKK个f(x)f(x)f(x),在优化理论中,相当于多变量优化,是一个极其难以优化的问题。所以使用(3)式这种贪婪的方式,每一次只优化一棵树。
L(t)=∑i=1nl(yi,y^i(t−1)+ft(xi))+Ω(ft)(3)\mathcal{L}^{(t)}=\sum_{i=1}^n l\left(y_i, \hat{y}_i^{(t-1)}+f_t\left(\mathbf{x}_i\right)\right)+\Omega\left(f_t\right)\tag{3} L(t)=i=1∑nl(yi,y^i(t−1)+ft(xi))+Ω(ft)(3)
yi^t\hat{y_i}^{t}yi^t:第iii个样本实例在第ttt次迭代的预测值;
注:二阶泰勒公式:
f(x+Δx)≈f(x)+f′(x)⋅Δx+12f′′(x)⋅Δx2f(x+\Delta x)\approx f(x)+f'(x)\cdot\Delta x+\dfrac{1}{2}f''(x)\cdot\Delta x^2 f(x+Δx)≈f(x)+f′(x)⋅Δx+21f′′(x)⋅Δx2
但是(3)式还是不容易优化,需要进行二阶近似:
L(t)≃∑i=1n[l(yi,y^(t−1))+gift(xi)+12hift2(xi)]+Ω(ft)(4)\mathcal{L}^{(t)} \simeq \sum_{i=1}^n\left[l\left(y_i, \hat{y}^{(t-1)}\right)+g_i f_t\left(\mathbf{x}_i\right)+\frac{1}{2} h_i f_t^2\left(\mathbf{x}_i\right)\right]+\Omega\left(f_t\right)\tag{4} L(t)≃i=1∑n[l(yi,y^(t−1))+gift(xi)+21hift2(xi)]+Ω(ft)(4)
gig_igi:gi=∂y^(t−1)l(yi,y^(t−1))g_i=\partial_{\hat{y}^{(t-1)}} l\left(y_i, \hat{y}^{(t-1)}\right)gi=∂y^(t−1)l(yi,y^(t−1))
hih_ihi:hi=∂y^(t−1)2l(yi,y^(t−1))h_i=\partial_{\hat{y}^{(t-1)}}^2 l\left(y_i, \hat{y}^{(t-1)}\right)hi=∂y^(t−1)2l(yi,y^(t−1))
进一步去掉常数项,得到损失函数:(常数项不影响损失函数,因为常数项不影响最小化损失函数问题,只会影响损失函数的结果的量级)
L~(t)=∑i=1n[gift(xi)+12hift2(xi)]+Ω(ft)(5)\tilde{\mathcal{L}}^{(t)}=\sum_{i=1}^n\left[g_i f_t\left(\mathbf{x}_i\right)+\frac{1}{2} h_i f_t^2\left(\mathbf{x}_i\right)\right]+\Omega\left(f_t\right)\tag{5} L~(t)=i=1∑n[gift(xi)+21hift2(xi)]+Ω(ft)(5)
按照叶子节点进行样本的集合划分:
L~(t)=∑i=1n[gift(xi)+12hift2(xi)]+γT+12λ∑j=1Twj2=∑j=1T[(∑i∈Ijgi)wj+12(∑i∈Ijhi+λ)wj2]+γT(6)\begin{aligned} \tilde{\mathcal{L}}^{(t)} & =\sum_{i=1}^n\left[g_i f_t\left(\mathbf{x}_i\right)+\frac{1}{2} h_i f_t^2\left(\mathbf{x}_i\right)\right]+\gamma T+\frac{1}{2} \lambda \sum_{j=1}^T w_j^2 \\ & =\sum_{j=1}^T\left[\left(\sum_{i \in I_j} g_i\right) w_j+\frac{1}{2}\left(\sum_{i \in I_j} h_i+\lambda\right) w_j^2\right]+\gamma T \end{aligned}\tag{6} L~(t)=i=1∑n[gift(xi)+21hift2(xi)]+γT+21λj=1∑Twj2=j=1∑Ti∈Ij∑giwj+21i∈Ij∑hi+λwj2+γT(6)
Ij={i∣q(xi)=j}I_j=\{i|q(\mathbf{x}_i)=j\}Ij={i∣q(xi)=j}:叶子节点jjj的样本集合;
然后对www求导数,令其==0,得到:
wj∗=−∑i∈Ijgi∑i∈Ijhi+λ,(7)w_j^*=-\dfrac{\sum_{i\in I_j}g_i}{\sum_{i\in I_j}h_i+\lambda},\tag{7} wj∗=−∑i∈Ijhi+λ∑i∈Ijgi,(7)
计算对应的优化值:
L~(t)(q)=−12∑j=1T(∑i∈Ijgi)2∑i∈Ijhi+λ+γT.(8)\tilde{\mathcal{L}}^{(t)}(q)=-\dfrac{1}{2}\sum\limits_{j=1}^{T}\dfrac{\left(\sum_{i\in I_j}g_i\right)^2}{\sum_{i\in I_j}h_i+\lambda}+\gamma T.\tag{8} L~(t)(q)=−21j=1∑T∑i∈Ijhi+λ(∑i∈Ijgi)2+γT.(8)
式(8)可以作为像决策树里面的纯度、信息熵一样的划分函数,得到树的划分分数。如图

通常应该计算单个叶子节点和添加左右节点的贪婪算法来评估是不是增加分支,而不能直接计算(8),如下:
Lsplit=12[(∑i∈ILgi)2∑i∈ILhi+λ+(∑i∈IRgi)2∑i∈IRhi+λ−(∑i∈Igi)2∑i∈Ihi+λ]−γ(9)\mathcal{L}_{split}=\dfrac{1}{2}\left[\dfrac{(\sum_{i\in I_L}g_i)^2}{\sum_{i\in I_L}h_i+\lambda}+\dfrac{(\sum_{i\in I_R}g_i)^2}{\sum_{i\in I_R}h_i+\lambda}-\dfrac{(\sum_{i\in I}g_i)^2}{\sum_{i\in I}h_i+\lambda}\right]-\gamma\tag{9} Lsplit=21[∑i∈ILhi+λ(∑i∈ILgi)2+∑i∈IRhi+λ(∑i∈IRgi)2−∑i∈Ihi+λ(∑i∈Igi)2]−γ(9)
R}h_i+\lambda}-\dfrac{(\sum_{i\in I}g_i)^2}{\sum_{i\in I}h_i+\lambda}\right]-\gamma\tag{9}
$$
相关文章:

xgboost:算法数学原理
xgboost算法数学原理 1、求预测值 y^iϕ(xi)∑k1Kfk(xi),fk∈F,(1)\hat{y}_i\phi\left(\mathbf{x}_i\right)\sum_{k1}^K f_k\left(\mathbf{x}_i\right), \quad f_k \in \mathcal{F},\tag{1} y^iϕ(xi)k1∑Kfk(xi),fk∈F,(1) F{f(x)wq(x)}(q:Rm→T,w∈RT)\mathca…...

map、multimap、unordered_map
引用:windows程序员面试指南 map map 红黑树 map 对value值无要求 map 有序,按照key值自动排序 map key值唯一 map 头文件:#include map 支持重载[]的运算符 map 为保持有序性,erase()开销大 multimap multimap 红黑树 multim…...

2023年全国最新会计专业技术资格精选真题及答案11
百分百题库提供会计专业技术资格考试试题、会计考试预测题、会计专业技术资格考试真题、会计证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 一、选择题 1.下列各项中,仅将生产过程中消耗的变动成本计入产品成本…...

Centos7搭建NFS
1.NFS简介Network File System(网络文件系统,通过网络让不同的机器系统之间可以彼此共享文件和目录,类似Samba服务。2.NFS挂载原理 在网络中服务器和客户端进行连接都是通过端口进行数据传输,而NFS服务端的端口是随机的,从而导致N…...
ThreadLoca基本使用以及与synchronized的区别
文章目录1. ThreadLocal介绍1.1 官方介绍1.2 基本使用1.2.1 常用方法1.2.2 使用案例1.3 ThreadLocal类与synchronized关键字1.3.1 synchronized同步方式1.3.2 ThreadLocal与synchronized的区别2. 运用场景_事务案例2.1 转账案例2.1.1 场景构建2.1.2 引入事务2.2 常规解决方案2.…...

【C++】纯虚函数、纯虚析构
纯虚函数语法:virtual 返回值类型 函数名(参数列表) 0纯虚函数的作用:不用定义!在多态中,通常父类中虚函数的实现是无意义的(因为主要用子类重写的,父类只是为了派生子类当做一个类族的顶层出现࿰…...

Python 进阶小技巧:7招展开嵌套列表
大家好,今天给大家讲解一个Python的进阶知识点:如何将一个嵌套的大列表展开形成一个列表。 小编提供了7种方法供大家学习参考: for循环 列表推导式 使用第三方库itertools 使用sum函数 python自加() 使用extend函…...

【Spring6】| Bean的作用域
目录 一:Bean的作用域 1. singleton(单例) 2. prototype(多例) 3. 其它scope 4. 自定义scop(了解) 一:Bean的作用域 1. singleton(单例) (1…...

Qt界面美化之自定义qss样式表
原生的QT界面不好看,有时候需要根据美工的设计图修改样式。如果使用QML的话搞界面是快,但是QML有点儿吃内存,有时简单的功能还是用传统c的widget方便些。好在有qss,传统界面也可以美化的。QSS称为Qt Style Sheets也就是Qt样式表&a…...

春招进行时:“211文科硕士吐槽工资5500” HR:行情和能力决定价值
学历重要,还是能力重要? 春招进行时,不少学生求职遇冷,会把原因归结为学历水平不够高、毕业院校不够档次、专业不够热门、非一线城市就业机会少等等。 直到上海一位211大学的文科男硕士,吐槽招聘会提供的岗位薪资待遇…...
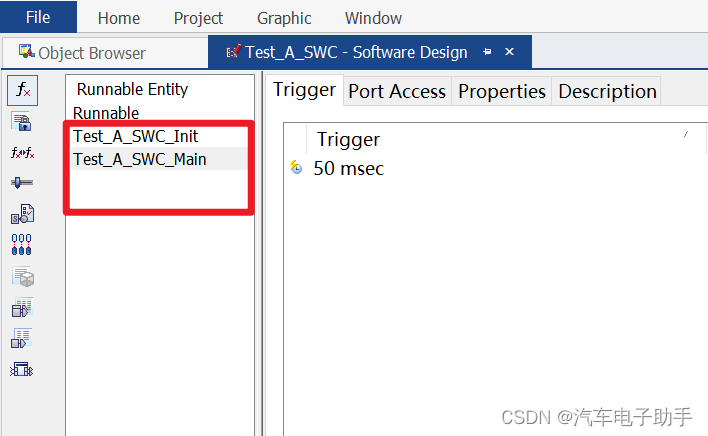
【DaVinci Developer专题】-45-自动生成SWC中所有Runnable对应的C文件
点击返回「Autosar从入门到精通-实战篇」总目录 案例背景(共5页精讲): 在DaVinci Developer中,以Test_A_SWC的Runnable为例,见图0-1。我们现在尝试自动生成一个包含Test_A_SWC_Init和Test_A_SWC_Main函数原型(也是适用于 C/S Port Serve Runnable)的C文件。 图0-1 目…...

redis启动和关闭服务脚本
编译安装redis,自己写了个脚本。 简单实现启动、关闭和 查看redis服务。 基本流程如下: 脚本执行,必须附带1个参数,没有参数会提示附带参数。 脚本会获取redis-server进程数量。作为开启、关闭以及查看redis服务的数据依据。 …...

windows CMD快捷键:
🐱个人主页:莎萌玩家🙋♂️作者简介:全栈领域新星创作者、专注于全栈各领域技术,共同学习共同进步,一起加油呀!💫系列专栏:网络爬虫、WEB全栈开发📢资料领取…...
【C/C++语言】刷题|双指针|数组|单链表
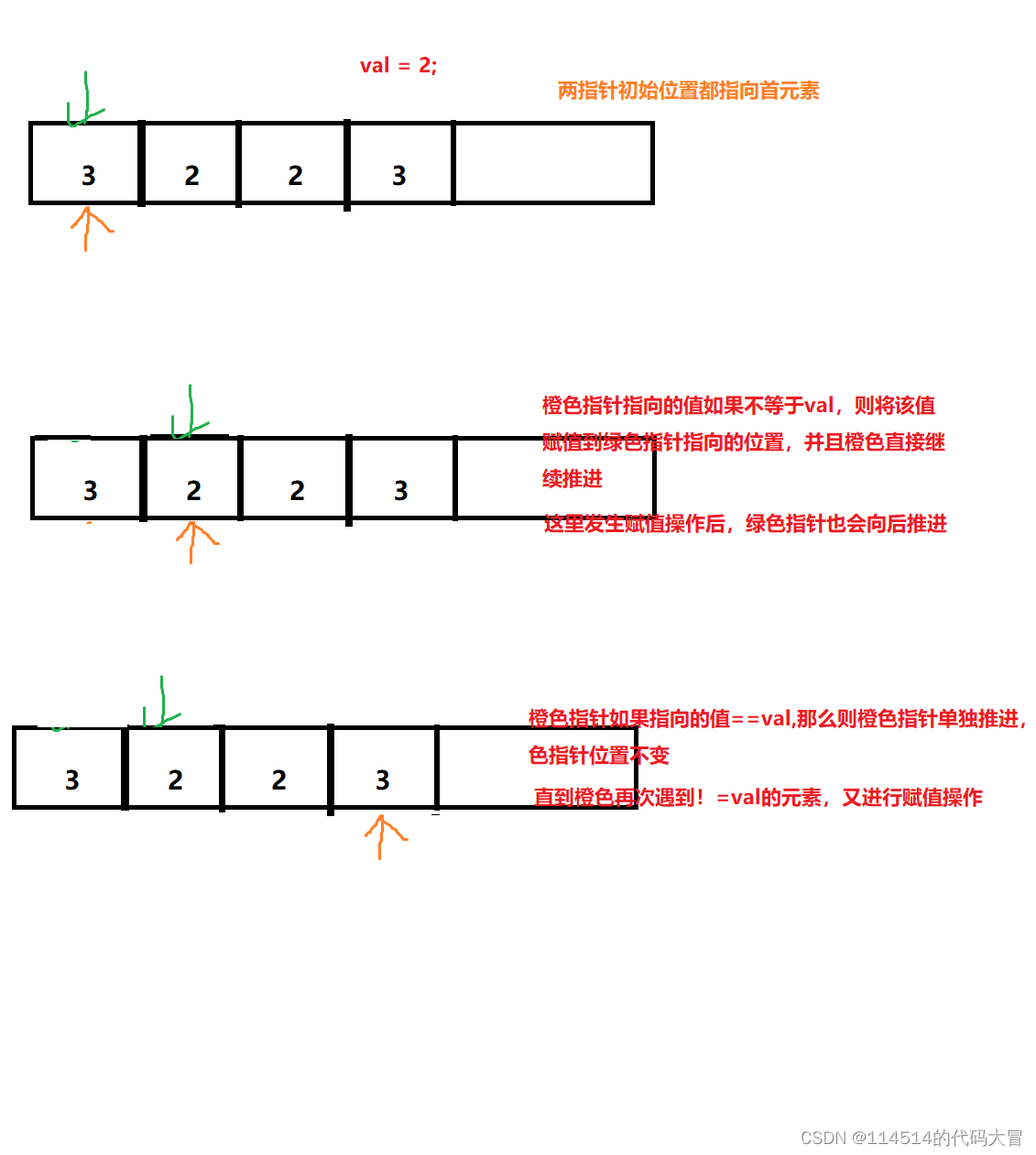
主页:114514的代码大冒 qq:2188956112(欢迎小伙伴呀hi✿(。◕ᴗ◕。)✿ ) Gitee:庄嘉豪 (zhuang-jiahaoxxx) - Gitee.com 文章目录 目录 文章目录 前言 一、删除有序数组中的重复项 二、合并两个有序数组 三,移除…...

Leetcode.1487 保证文件名唯一
题目链接 Leetcode.1487 保证文件名唯一 Rating : 1697 题目描述 给你一个长度为 n的字符串数组 names。你将会在文件系统中创建 n个文件夹:在第 i 分钟,新建名为 names[i]的文件夹。 由于两个文件 不能 共享相同的文件名,因此如…...
-双星号(**)-函数动态参数匹配-解包操作)
python-星号(*)-双星号(**)-函数动态参数匹配-解包操作
文章目录1.乘法和幂运算符2.函数接收数量不固定的入参3.限制函数入参仅以关键字形式输入4. 可迭代对象解包操作5.扩展可迭代对象解包1.乘法和幂运算符 ● 单个 * 用于乘法运算 ● 两个 ** 表示幂运算 >>> 2*3 >>> 6 >>> 2**3 >>> 82.函数…...

面试官:为什么说ArrayList线程不安全?
本博客知识点收录于:⭐️《JavaSE系列教程》⭐️ 1)线程安全与不安全集合 我们学习集合的时候发现集合存在由线程安全集合和线程不安全集合;线程安全效率低,安全性高;反之,线程不安全效率高,安…...
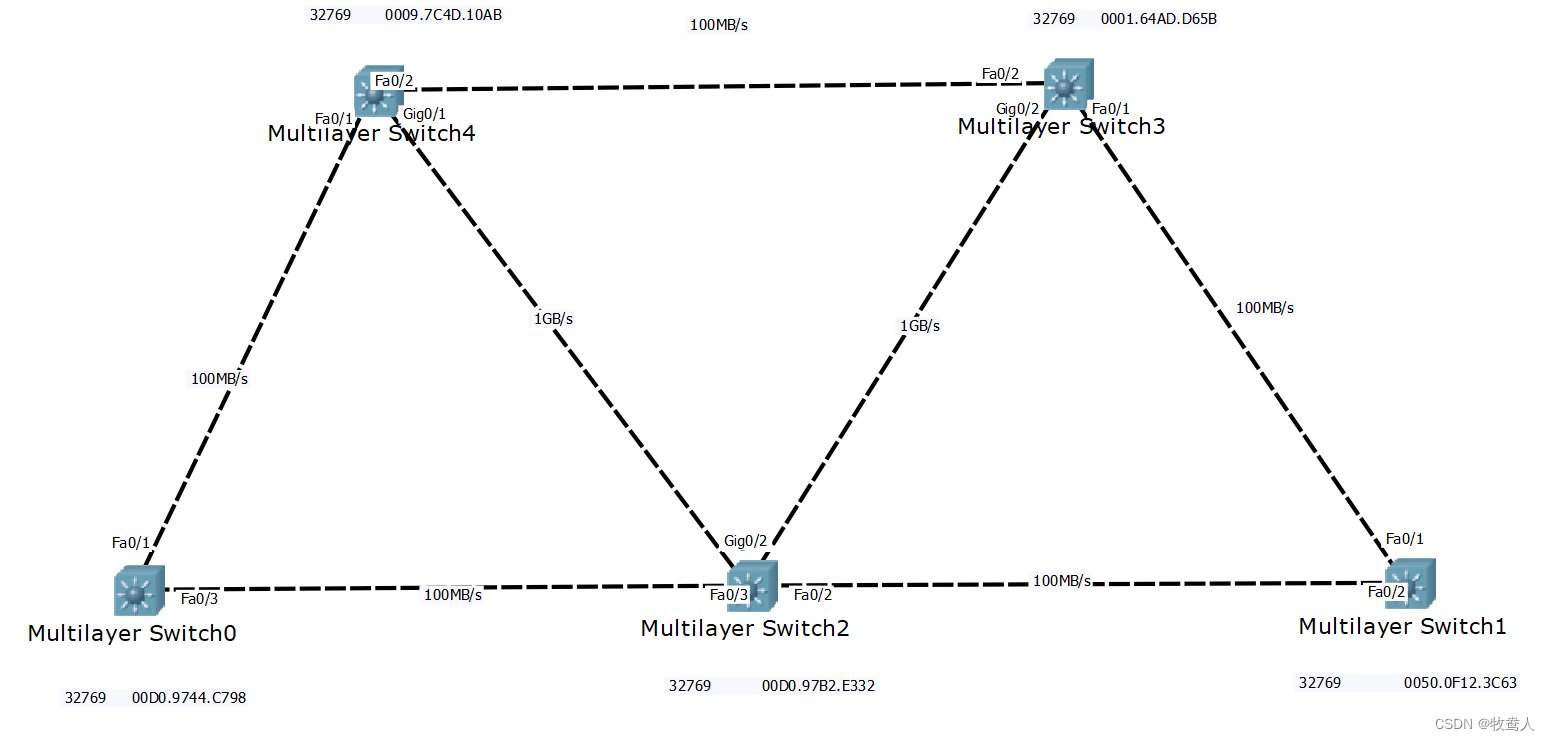
STP详解
STP STP全称为“生成树协议”(Spanning Tree Protocol),是一种网络协议,用于在交换机网络中防止网络回路产生,保证网络的稳定和可靠性。它通过在网络中选择一条主路径(树形结构),并…...

linux AWK常用命令 —— 筑梦之路
搜集整理awk常用命令,以便使用查询 # 打印文件第一列awk {print $1} rumenz.txt# 打印文件前两列awk {print $1,$2} rumenz.txt# 打印文件最后一列awk {print $NF} rumenz.txt# 打印文件总行数awk END{print NR} rumenz.txt# 打印文件第一行awk NR1{print} rumenz.…...
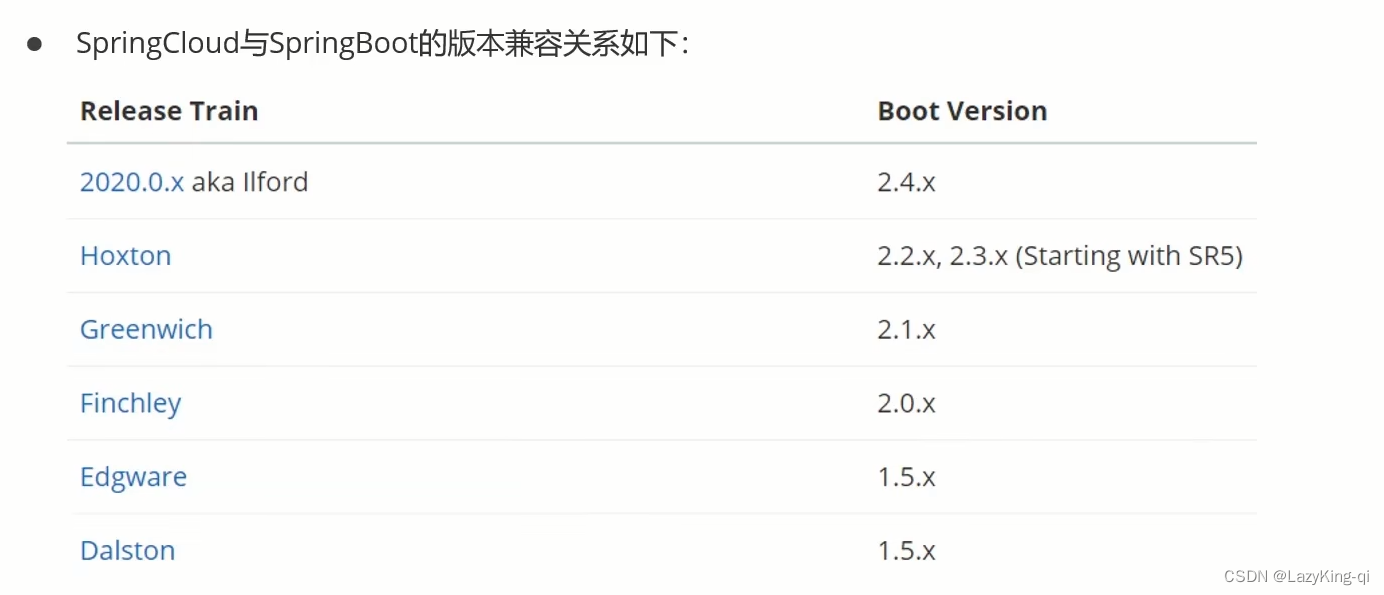
SpringCloud:服务拆分及远程调用
目录 SpringCloud:服务拆分及远程调用 1、服务拆分 2、远程调用 SpringCloud:服务拆分及远程调用 SpringCloud是目前国内使用最广泛的微服务框架。 官网地址: Spring Cloud SpringCloud集成了各种微服务功能组件,并基于SpringBoot实现了…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...
