【机器学习】西瓜书第6章支持向量机课后习题6.1参考答案
【机器学习】西瓜书学习心得及课后习题参考答案—第6章支持向量机
1.试证明样本空间中任意点x到超平面(w,b)的距离为式(6.2)。
首先,直观解释二维空间内点到直线的距离:

由平面向量的有关知识,可得:
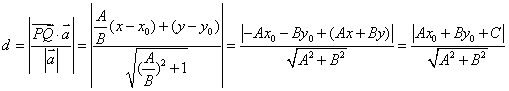
超平面的法向量为 w w w,任取平面上一点 x 0 x_0 x0,则超平面可以表示为 ω T ⋅ x 0 + b = 0 ω^T \cdot x_0 + b = 0 ωT⋅x0+b=0。一个点 x x x到超平面的距离可以用该点到 x 0 x_0 x0 的距离在法向量 (ω) 方向上的投影来表示,即:
距离 = ∣ ω T ( x − x 0 ) ∣ ∣ ∣ ω ∣ ∣ = ∣ ω T x + b ∣ ∣ ∣ ω ∣ ∣ \text{距离} = \frac{|ω^T(x−x_0)|}{||ω||} = \frac{|ω^T x + b|}{||ω||} 距离=∣∣ω∣∣∣ωT(x−x0)∣=∣∣ω∣∣∣ωTx+b∣
其中:
- ω T ω^T ωT 表示向量 w w w 的转置。
- ∣ ∣ ω ∣ ∣ ||ω|| ∣∣ω∣∣ 表示向量 w w w 的范数(模长)。
- x x x 是指向平面上的任意点。
- x 0 x_0 x0 是平面上的某一点。
- b b b 是平面的偏置项。
这个公式表示了点 x x x 到平面的距离,计算方式是将点 x x x 投影到法向量 ω ω ω 上,然后除以 ω ω ω 的模长。
其中 ω = ( ω_1; ω_2; … ; ωd) 为法向量,决定了超平面的方向 ; b b b 为位移项,决定
了超平面与原点之间的距离.
相关文章:
【机器学习】西瓜书第6章支持向量机课后习题6.1参考答案
【机器学习】西瓜书学习心得及课后习题参考答案—第6章支持向量机 1.试证明样本空间中任意点x到超平面(w,b)的距离为式(6.2)。 首先,直观解释二维空间内点到直线的距离: 由平面向量的有关知识,可得: 超平面的法向量为 w w w&am…...

【OpenAI Q* 超越人类的自主系统】DQN :Q-Learning + 深度神经网络
深度 Q 网络:用深度神经网络,来近似Q函数 强化学习介绍离散场景,使用行为价值方法连续场景,使用概率分布方法实时反馈连续场景:使用概率分布 行为价值方法 DQN(深度 Q 网络) 深度神经网络 Q-L…...

Vue axios Post请求 403 解决之道
前言: 刚开始请求的时候报 CORS 错误,通过前端项目配置后算是解决了,然后,又开始了新的报错 403 ERR_BAD_REQUEST。但是 GET 请求是正常的。 后端的 Controller 接口代码如下: PostMapping(value "/login2&qu…...
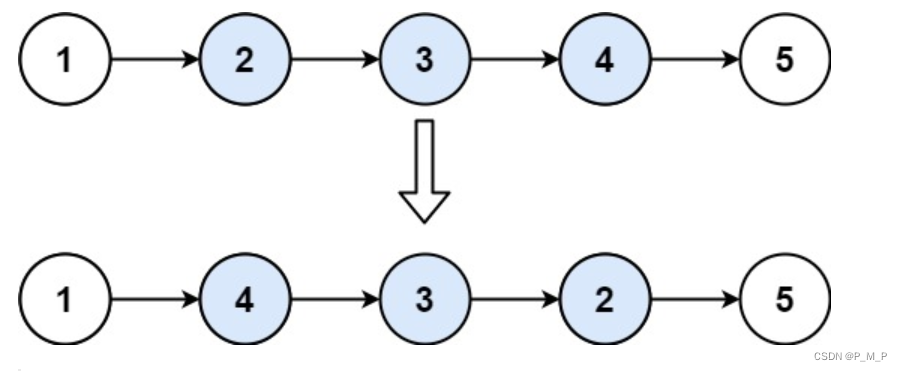
【Leetcode】重排链表、旋转链表、反转链表||
目录 💡重排链表 题目描述 方法一: 方法二: 💡旋转链表 题目描述 方法: 💡反转链表|| 题目描述 方法: 💡总结 💡重排链表 题目描述 给定一个单链表 L 的头节…...
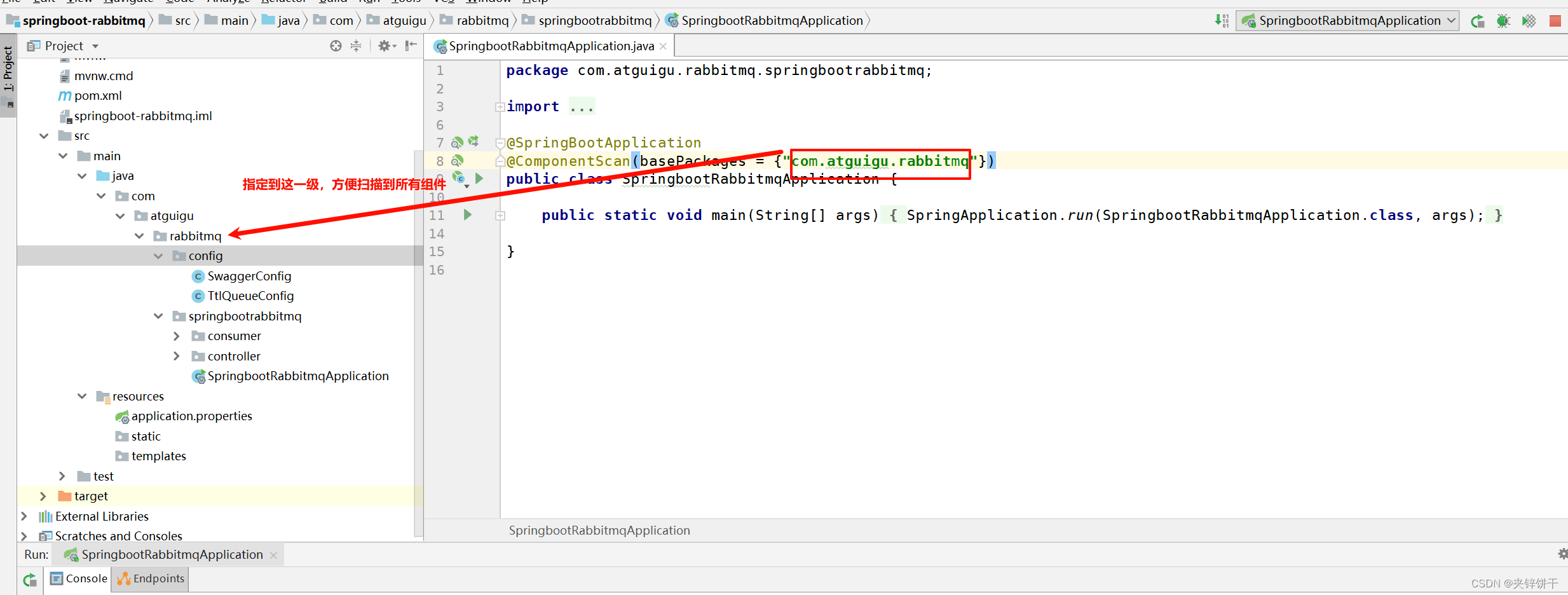
RabbitMQ 报错:Failed to declare queue(s):[QD, QA, QB]
实在没想到会犯这种低级错误。 回顾整理一下吧: 原因:SpringBoot主配置类默认只会扫描自己所在的包及其子包下面的组件。其他位置的配置不会被扫描。 如果非要使用其他位置,就需要在启动类上面指定新的扫描位置。注意新的扫描位置会覆盖默…...
Neo4j 5建库
Neo4j 只有企业版可以运行多个库,社区版无法创建多个库,一个实例只能运行一个库; 如果业务需要使用多个库怎么办呢? 就是在一个机器上部署多个实例,每个实例单独一个库名 这个库的名字我们可以自己定义; …...

鲁棒最小二乘法 拟合圆
圆拟合算法_基于huber加权的拟合圆算法-CSDN博客 首次拟合圆得到采用的上述blog中的 Ksa Fit 方法。 该方法存在干扰点时,拟合得到的结果会被干扰。 首次拟合圆的方法 因此需要针对外点增加权重因子,经过多次迭代后&…...

LeetCode——动态规划
动态规划 一、一维数组:斐波那契数列 爬楼梯70简单 dp定义: dp[i]表示爬到第i阶有多少种不同的方式 状态转移方程: dp[i] dp[i-1] dp[i-1] (每次可以爬1或2个台阶) 边界条件: dp[0] 1; dp[1] 1;&#…...

opencv和gdal的读写图片波段顺序问题
最近处理遥感影像总是不时听到 图片的波段错了,一开始不明就里,都是图片怎么就判断错了。 1、图像RGB波段顺序判断 后面和大家交流,基本上知道了一个判断标准。 一般来说,进入人眼的自然画面在计算机视觉中一般是rgb波段顺序表示…...

PyQt 打包成exe文件
参考链接 Python程序打包成.exe(史上最全面讲解)-CSDN博客 手把手教你将pyqt程序打包成exe(1)_pyqt exe-CSDN博客 PyInstaller 将DLL文件打包进exe_怎么把dll文件加到exe里-CSDN博客 自己的问题 按照教程走的话,会出现找不到“mmdeploy_ort_net.dll”文件的报错…...
)
【Web2D/3D】SVG(第二篇)
1. 前言 SVG(Scalable Vector Graphics,可缩放矢量图形)是一种使用XML描述2D图形的语言,由于SVG是基于XML(HTML也是基于XML的),因为SVG DOM中每个元素都是可以操作的,包含修改元素属…...

leetcode18. 四数之和
题目描述 给你一个由 n 个整数组成的数组 nums ,和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]] (若两个四元组元素一一对应,则认为两个四元组重复): …...
(十八)Flask之threaing.local()对象
0、引子: 如下是一段很基础的多线程代码: from threading import Threaddemo 0def task(arg):global demodemo argprint(demo)for i in range(10):t Thread(targettask, args(i, ))t. start()当程序运行时,可能会看到输出的顺序是混乱的…...
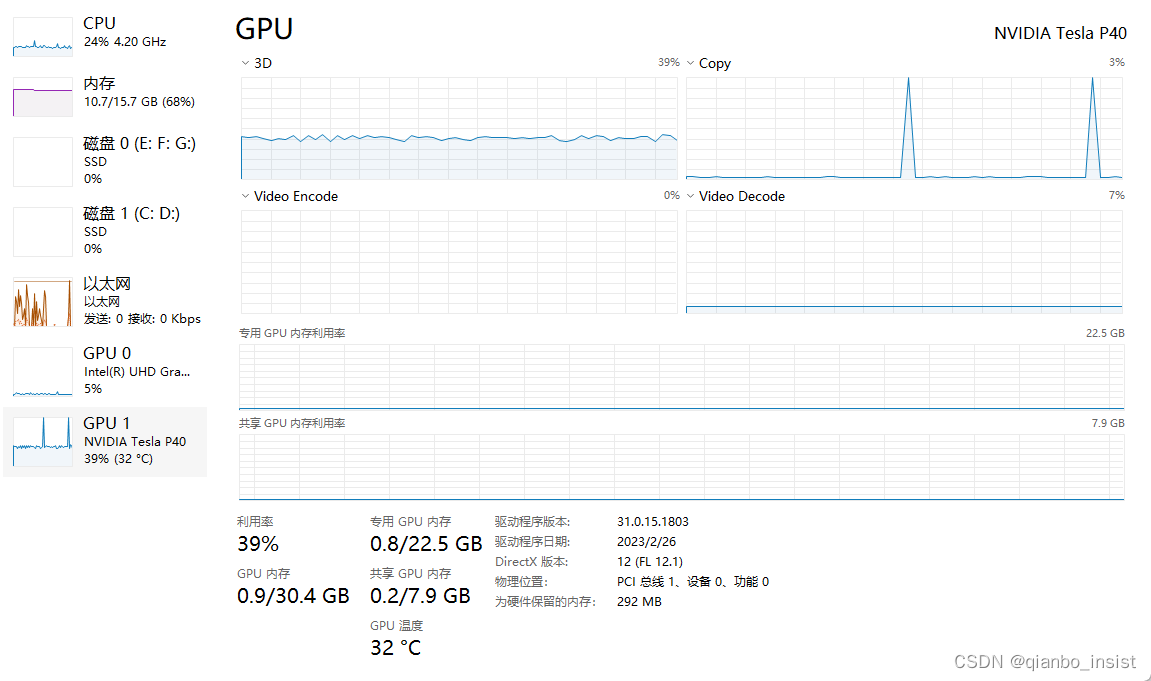
ffmpeg 硬件解码零拷贝unity 播放
ffmpeg硬件解码问题 ffmpeg 在硬件解码,一般来说,我们解码使用cuda方式,当然,最好的方式是不要确定一定是cuda,客户的显卡不一定有cuda,windows 下,和linux 下要做一些适配工作,最麻…...
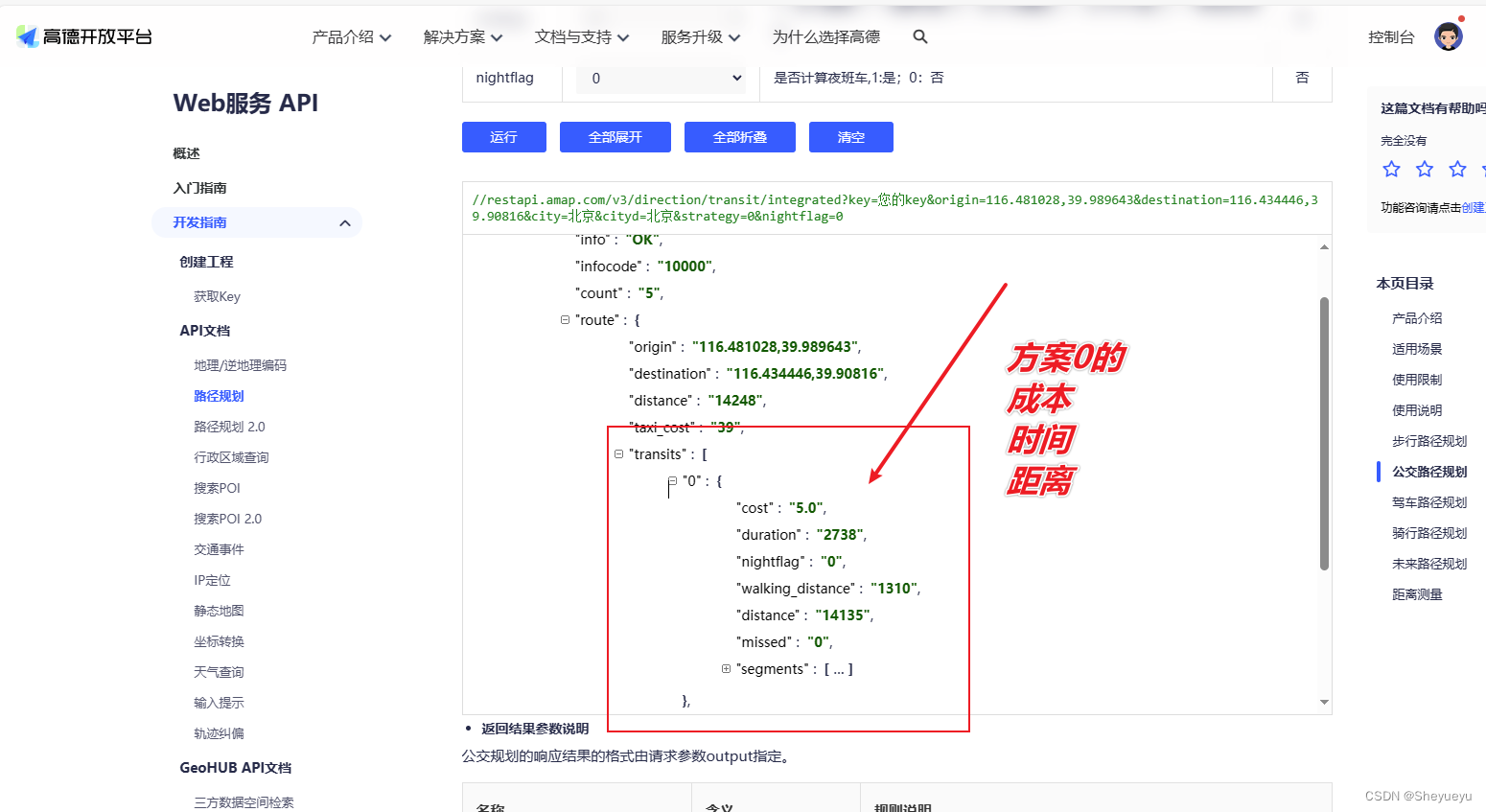
高德地图_公共交通路径规划API,获取两地点之间的驾车里程和时间
import pandas as pd import requests import jsondef get_dis_tm(origin, destination,city,cityd):url https://restapi.amap.com/v3/direction/transit/integrated?key xxx #这里就是需要去高德开放平台去申请key,请在xxxx位置填写,web服务APIlink {}origin{}&desti…...

PyTorch深度学习实战(28)——对抗攻击(Adversarial Attack)
PyTorch深度学习实战(28)——对抗攻击 0. 前言1. 对抗攻击2. 对抗攻击模型分析3. 使用 PyTorch 实现对抗攻击小结系列链接 0. 前言 近年来,深度学习在图像分类、目标检测、图像分割等诸多领域取得了突破性进展,深度学习模型已经能…...
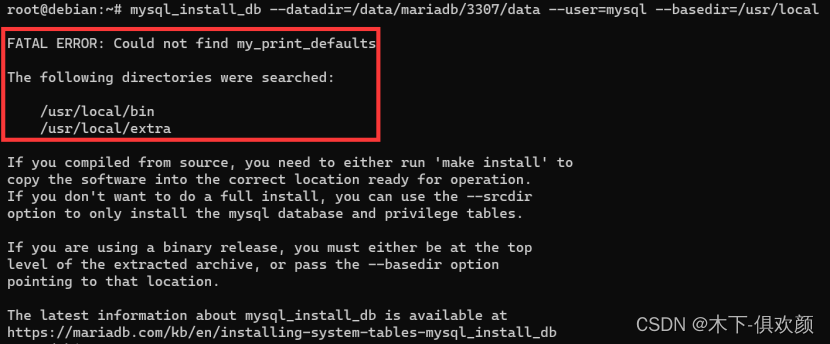
MariaDB单机多实例的配置方法
1、什么是数据库的单机多实例 数据库的单机多实例是指在一台物理服务器上运行多个数据库实例。这种部署方式允许多个数据库实例共享相同的物理资源,如CPU、内存和存储,从而提高硬件利用率并降低成本。每个数据库实例可以独立运行,处理不同的…...
加强->servlet->tomcat
0什么是servlet jsp也是servlet 细细体会 Servlet 是 JavaEE 的规范之一,通俗的来说就是 Java 接口,将来我们可以定义 Java 类来实现这个接口,并由 Web 服务器运行 Servlet ,所以 TomCat 又被称作 Servlet 容器。 Servlet 提供了…...

Python初学者必须吃透的69个内置函数!
所谓内置函数,就是Python提供的, 可以直接拿来直接用的函数,比如大家熟悉的print,range、input等,也有不是很熟,但是很重要的,如enumerate、zip、join等,Python内置的这些函数非常精巧且强大的&…...
Day73力扣打卡
打卡记录 统计移除递增子数组的数目 II(双指针) 链接 class Solution:def incremovableSubarrayCount(self, a: List[int]) -> int:n len(a)i 0while i < n - 1 and a[i] < a[i 1]:i 1if i n - 1: # 每个非空子数组都可以移除return n …...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...
