图论 经典例题
1 拓扑排序
对有向图的节点排序,使得对于每一条有向边 U-->V U都出现在V之前
*有环无法拓扑排序
indegree[], nxs[];//前者表示节点 i 的入度,后者表示节点 i 指向的节点
queue = []
for i in range(n):if indege[i] == 0: queue.add(i)// 入度为0的节点加入队列
while queue:curnode = queue.popleft()for nx in nxs[curnode]:indegre[nx] -= 1;if indegre[nx] == 0:queue.add(nx);207 课程表1
#include <vector>
#include <deque>using namespace std;class Solution {
public:bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {// 邻接表vector<vector<int>> nxs(numCourses, vector<int>());// 入度数组vector<int> indegree(numCourses, 0);// 填充入度数组和邻接表for (auto pre : prerequisites) {int a = pre[0];int b = pre[1];// a 的入度增加indegree[a]++;// 将 b 加入 a 的邻接表nxs[b].push_back(a);}deque<int> q;// 1.找到入度为0的点for (int i = 0; i < numCourses; i++) {if (indegree[i] == 0) {q.push_back(i);}}// 2.迭代,更新入度while (!q.empty()) {int curr = q.front();q.pop_front();numCourses--; // 完成一个课程for (int neighbor : nxs[curr]) {if (--indegree[neighbor] == 0) {q.push_back(neighbor);}}}// 如果所有课程都完成了,则返回 truereturn numCourses == 0;}
};210 课程表II
class Solution {
public:vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {// 邻接表vector<vector<int>> nxs (numCourses, vector<int>());// 入度数组vector<int> indegree (numCourses);// 填充入度数组和邻接表for (auto pre : prerequisites) {int a = pre[0];int b = pre[1];indegree[a]++;nxs[b].push_back(a);}vector<int> res;deque<int> q;int index = 0;for (int i = 0; i < numCourses; ++i) {if (indegree[i] == 0) {q.push_back(i);}}while (!q.empty()) {int k = q.front();q.pop_front();res.push_back(k);index++;for (auto neg : nxs[k]) {if (--indegree[neg] == 0) {q.push_back(neg); }}}if (index != numCourses) {return vector<int>();}else{return res;} }
};310 最小高度树
依次删去度数为 1 的点
class Solution {
public:vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {// 找到使得树的高度最小的节点// 找到最中间的点if (n == 1) return vector<int>({0});// 储存度数,而非入度vector<int> degrees(n, 0);// 邻接表vector<vector<int>> adjacencyList(n, vector<int>());for (auto edge : edges) {int a = edge[0];int b = edge[1];degrees[a]++;degrees[b]++;adjacencyList[a].push_back(b);adjacencyList[b].push_back(a);}// 队列,储存入度为 1deque<int> q;// 找到度数为 1 的点for (int i = 0; i < n; ++i) {if (degrees[i] == 1) {q.push_back(i);}}vector<int> res;// 遍历所有边缘节点while (!q.empty()) {res.clear();// 层序更新,这一批点处理完之后,先看结果对不对int len = q.size();for (int i = 0; i < len; ++i) {int node = q.front();q.pop_front();res.push_back(node);// 更新两个矩阵for (auto nex : adjacencyList[node]) {degrees[nex]--;if (degrees[nex] == 1){q.push_back(nex);}}}}return res;}
};
802 逆向拓扑
找到不能进入环的点,跟它在不在环里面没关系
有向图找环
从出度为 0 的点出发,它们不可能在环中
class Solution {
public:vector<int> eventualSafeNodes(vector<vector<int>>& graph) {int n = graph.size();// 出度vector<int> outdegree(n);// 逆向邻接表vector<vector<int>> pre_nodes(n, vector<int>());for (int i = 0; i < n; ++i) {for (auto nx : graph[i]) {// i --> nxoutdegree[i]++;pre_nodes[nx].push_back(i);}}deque<int> q;// 找到出度为 0 的点for (int i = 0; i < n; ++i) {if (outdegree[i] == 0) {q.push_back(i);}}// 储存结果vector<int> res;while (!q.empty()) {int node = q.front();q.pop_front();res.push_back(node);for (auto nex : pre_nodes[node]) {outdegree[nex]--;if (outdegree[nex] == 0) {q.push_back(nex);}}}sort(res.begin(), res.end());return res;}
};2 并查集
查找连通块的数量
int[] fa;void init(int n) {fa = new int[n];// 初始化for (int i = 0; i < n; ++i) fa[i] = i;// 遍历,都指向自己
}// 0 和 3 是亲戚,则 0 和 3建立链接
int find(int x) {// 如果 x 是自己的 boss 则返回 x// 如果不是,则 return x == fa[x] ? x : (fa[x] = find(fa[x]));// 是否是根节点
}void union(int x, int y) {fa[find(x)] = find(y);// 连通
} vector<int> fa; // 并查集的父节点数组// 初始化并查集,设置每个节点的父节点为自己// 0 -- n-1void init(int n) {fa.resize(n);for (int i = 0; i < n; ++i) {fa[i] = i;}}// 查找节点x所在的集合的根节点,同时进行路径压缩int find(int x) {return x == fa[x] ? x : (fa[x] = find(x));}// 合并两个节点所在的集合void uni(int x, int y) {fa[find(x)] = find(y);}构建并查集的操作基本都是一样的
1.查询根节点 + 路径压缩
2.合并块
题眼一般是多个集合的合并
547 省份数量
并查集 + 求连通块的数量
class Solution {
public:vector<int> fa;// 初始化 n 个城市的父节点为它们自己void init(int n) {fa.resize(n, 0);for (int i = 0; i < n; ++i) {fa[i] = i;}}// 找 x 的夫节点int find(int x) {return x == fa[x] ? x : (fa[x] = find(fa[x]));}// 合并void uni(int x, int y) {fa[find(x)] = find(y);}// 判断多少个根节点int findCircleNum(vector<vector<int>>& isConnected) {int n = isConnected.size();// 初始化init(n);for (int i = 0; i < n; ++i){for (int j = i + 1; j < n; ++j) {if (isConnected[i][j] == 1) uni(i, j);}}// 检查最后有几个点的父节点是它自己,即根的数目int cnt = 0;for (int i = 0; i < n; ++i) {if (fa[i] == i) {cnt++;}}return cnt;}
};684 冗余连接
根据父节点的特点找冗余路径
class Solution {
public:vector<int> fa;// 节点是 1 -- nvoid init(int n) {fa.resize(n + 1, 0);for (int i = 1; i <= n; ++i) {fa[i] = i;}}int find(int x) {return fa[x] == x ? x : find(fa[x]);}void uni(int x, int y) {fa[find(x)] = find(y);}vector<int> findRedundantConnection(vector<vector<int>>& edges) {int n = edges.size();init(n);for (auto edge : edges) {int a = edge[0];int b = edge[1];// 如果父类节点都一样,那么找到了冗余路径if (find(a) == find(b)) {return edge;} else {uni(a, b);}}return vector<int>();}
};1319
先连通,看连通块的数量,连接 n 个块需要 n - 1 个边
class Solution {
public:vector<int> fa;void init(int n) {fa.resize(n);for (int i = 0; i < n; ++i) {fa[i] = i;}}int find(int x) {return fa[x] == x ? x : (fa[x] = find(fa[x]));}void uni(int x, int y) {fa[find(x)] = find(y);}int makeConnected(int n, vector<vector<int>>& connections) {// 判断端点是否连通// 如果已经连通可以拆除// 连接 n 个连通块需要 n - 1 个边init(n);int cnt = 0;for (auto con : connections) {int a = con[0];int b = con[1];if (find(a) == find(b)) {cnt++;}else{uni(a, b);}}// 判断连通块的数量int num = 0; // 初始化for (int i = 0; i < n; ++i) {if (fa[i] == i) {num++;}}// 判断边是不是够用if (cnt >= num - 1) {return num - 1;}return -1;}
};水域大小
变体,需要维护连通块的数量
class Solution {
public:// 需要维护每个连通块的数量vector<int> fa;vector<int> cnts;// 只对根节点生效void init(int n) {fa.resize(n);cnts.resize(n);for (int i = 0; i < n; ++i) {fa[i] = i;cnts[i] = 1;}}int find(int x) {return fa[x] == x ? x : (fa[x] = find(fa[x]));}void uni(int x, int y) {int xp = fa[find(x)], yp = find(y);fa[xp] = yp;cnts[yp] += cnts[xp];}int getId(int x, int y, int col) {return x * col + y;}vector<int> pondSizes(vector<vector<int>>& land) {// x * col + y// 表示八个方向的方向数组vector<vector<int>> dirs = {{0, 1}, // 向右{0, -1}, // 向左{1, 0}, // 向下{-1, 0}, // 向上{1, 1}, // 右下{1, -1}, // 右上{-1, 1}, // 左下{-1, -1} // 左上};int n = land.size();int m = land[0].size();init(n * m);for (int i = 0; i < n; ++i) {for (int j = 0; j < m; ++j) {if (land[i][j] == 0) {for (auto dir : dirs) {// 遍历八个方向int nx = i + dir[0];int ny = j + dir[1];// 如果方向不越界 且 为水域if (nx < 0 || ny < 0 || nx >= n || ny >= m || land[nx][ny] != 0) {continue;}else{int id1 = getId(i, j, m);int id2 = getId(nx, ny, m);if (find(id1) != find(id2)) {uni(id1, id2);}}}}}}vector<int> res;for (int i = 0; i < n; ++i) {for (int j = 0; j < m; ++j) {int id = getId(i, j, m);if (fa[id] == id && land[i][j] == 0) {res.push_back(cnts[id]);}}}sort(res.begin(), res.end());return res;}
};721 账户合并(字符串)
建立映射 [0, a, b] 其中 0 代表人名,a 代表邮箱地址
最后还要倒过来输出
#include <vector>
#include <string>
#include <map>
#include <algorithm>class Solution {
public:// 并查集代码vector<int> fa; // 并查集的父节点数组// 初始化并查集,设置每个节点的父节点为自己void init(int n) {fa.resize(n);for (int i = 0; i < n; ++i) {fa[i] = i;}}// 查找节点x所在的集合的根节点,同时进行路径压缩int find(int x) {return x == fa[x] ? x : find(fa[x]);}// 合并两个节点所在的集合void uni(int x, int y) {fa[find(x)] = find(y);}vector<vector<string>> accountsMerge(vector<vector<string>>& accounts) {int n = accounts.size(); // 账号的数量init(n); // 初始化并查集// 邮箱到账号ID的映射map<string, int> email_accId;// 构建并查集,合并具有相同邮箱地址的账号for (int accId = 0; accId < n; accId++) {int m = accounts[accId].size(); // 当前账号的邮箱数量for (int i = 1; i < m; ++i) {string email = accounts[accId][i]; // 获取邮箱地址// 如果邮箱地址不存在,建立映射关系// if (email_accId.find(email) == email_accId.end()) {email_accId[email] = accId; } else {// 当前id和之前id合并uni(accId, email_accId[email]); // 如果邮箱地址已存在,合并账号}}}// 账号ID到邮箱的映射map<int, vector<string>> accId_emails;// 遍历所有邮箱账号,将它们归类到相同的账号ID下for (auto& pair : email_accId) {string email = pair.first;int accId = find(pair.second); // 获取根账号IDaccId_emails[accId].push_back(email);}// 构建最终的合并后的账户列表vector<vector<string>> mergedAccounts;for (auto& pair : accId_emails) {int accId = pair.first;vector<string> emails = pair.second;// 将账号ID添加到前面vector<string> mergedAccount = {accounts[accId][0]};sort(emails.begin(), emails.end()); // 对邮箱地址排序mergedAccount.insert(mergedAccount.end(), emails.begin(), emails.end());mergedAccounts.push_back(mergedAccount);}return mergedAccounts; // 返回合并后的账户列表}
};
相关文章:

图论 经典例题
1 拓扑排序 对有向图的节点排序,使得对于每一条有向边 U-->V U都出现在V之前 *有环无法拓扑排序 indegree[], nxs[];//前者表示节点 i 的入度,后者表示节点 i 指向的节点 queue [] for i in range(n):if indege[i] 0: queue.add(i)// 入度为0的节…...
Oracle数据updater如何回滚
1.查询update语句执行的时间节点 ; select t.FIRST_LOAD_TIME, t.SQL_TEXT from v$sqlarea t where to_char(t.FIRST_LOAD_TIME) > 2023-03-19/17:00:00 order by t.FIRST_LOAD_TIME desc;开启表的行迁移 alter table test enable row movement;3.回滚表数据到…...

redis开启密码验证
开启密码验证 (1)配置文件中设置 redis.conf文件里面配置requirepass参数,redis认证密码:foobared,然后重启redis服务 ./redis-cli 127.0.0.1:6379> 127.0.0.1:6379> 127.0.0.1:6379> CONFIG SET requi…...
一种删除 KubeSphere 中一直卡在 Terminating 的 Namespace--KubeSphere Logging System的简单方法
文章目录 一、问题提出二、删除方法1,获取kubesphere-logging-syste的详细信息json文件2,编辑kubesphere-logging-system.json3,执行清理命令 三、检查结果 一、问题提出 在使用 KubeSphere 的时候发现有一个日志服务KubeSphere Logging Sys…...

Flink1.17实战教程(第七篇:Flink SQL)
系列文章目录 Flink1.17实战教程(第一篇:概念、部署、架构) Flink1.17实战教程(第二篇:DataStream API) Flink1.17实战教程(第三篇:时间和窗口) Flink1.17实战教程&…...

nest定时任务调用service报错
报错: ERROR [Scheduler] ValidationError: Using global EntityManager instance methods for context specific actions is disallowed. If you need to work with the global instances identity map, use allowGlobalContext configuration option or fork() i…...
[Angular] 笔记 11:可观察对象(Observable)
chatgpt: 在 Angular 中,Observables 是用于处理异步数据流的重要工具。它们被广泛用于处理从异步操作中获取的数据,比如通过 HTTP 请求获取数据、定时器、用户输入等。Observables 提供了一种机制来订阅这些数据流,并可以在数据到达时执行相…...
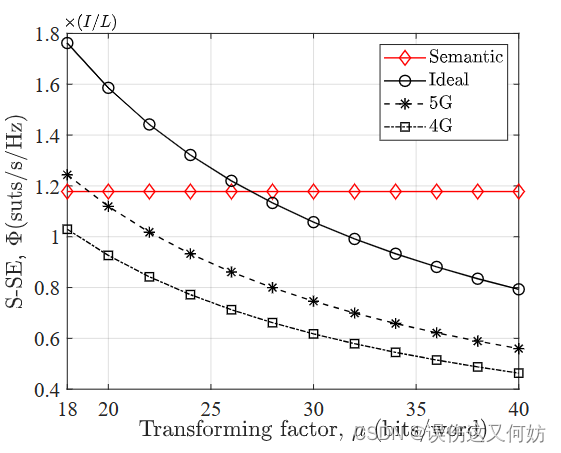
【论文阅读】Resource Allocation for Text Semantic Communications
这是一篇关于语义通信中资源分配的论文。全文共5页,篇幅较短。 目录在这里 摘要关键字引言语义通信资源分配贡献公式符号 系统模型DeepSC TransmitterTransmission ModelDeepSC Receiver 语义感知资源分配策略Semantic Spectral Efficiency (S-SE&#…...
VMware16 pro 安装openEuler-23.09-x86_64,详细操作流程+详图。
1.环境: win11, vmware16 pro, openEuler-23.09-x86_64-dvd.iso 社区版openEuler 23.09官方下载地址: openEuler下载 | 欧拉系统ISO镜像 | openEuler社区官网欧拉操作系统(openEuler, 简称“欧拉”)是面向数字基础设施的操作系统,支持服务器、云计算、…...

Mybatis 动态 SQL - script,bind,多数据库支持
script 在使用注解的映射器类中使用动态SQL时,可以使用<script>元素。例如: Update({"<script>","update Author"," <set>"," <if testusername ! null>username#{username},</if&g…...

Scikit-Learn线性回归(一)
Scikit-Learn线性回归一 1、线性回归概述1.1、回归1.2、线性1.3、线性回归1.4、线性回归的优缺点1.5、线性回归与逻辑回归2、线性回归的原理2.1、线性回归的定义与原理2.2、线性回归的损失函数3、Scikit-Learn线性回归3.1、Scikit-Learn库3.2、Scikit-Learn线性回归API3.3、Sci…...

Mybatis 动态 SQL - choose, when, otherwise
有时候我们并不希望所有的条件都生效,而是只想在多个选项中选择一个。类似于Java中的switch语句,MyBatis提供了 <choose>元素。 让我们使用上面的例子,但现在如果提供了标题,则只搜索标题;如果提供了作者&a…...
idea Spring Boot项目使用JPA创建与数据库链接
1.pom.xml文件中添加依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-jpa</artifactId></dependency><dependency><groupId>com.mysql</groupId><artifactId>…...
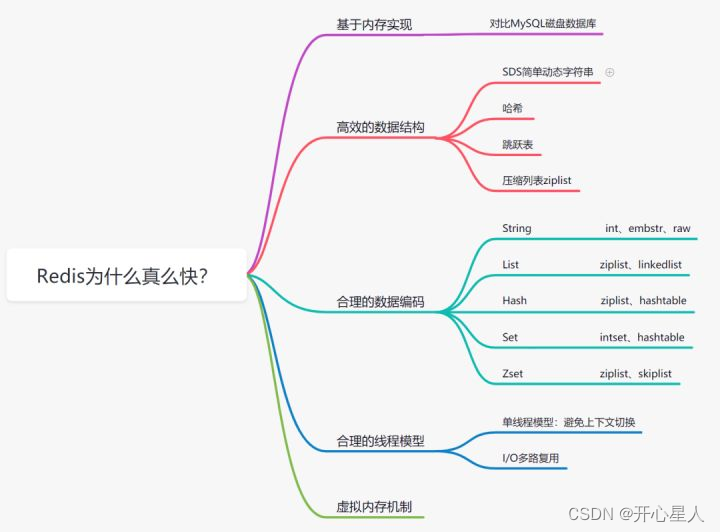
redis基础知识
学一点,整一点,基本都是综合别人的,弄成我能理解的内容 https://blog.csdn.net/liqingtx/article/details/60330555 https://blog.csdn.net/u014723137/article/details/125658176 https://redis.io/commands/ 官方命令 📌导航小助…...
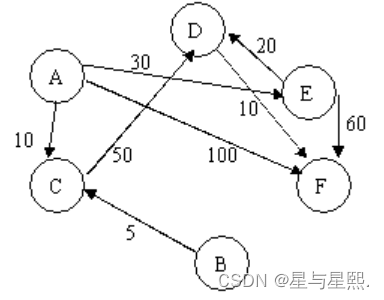
最短路径(数据结构实训)(难度系数100)
最短路径 描述: 已知一个城市的交通路线,经常要求从某一点出发到各地方的最短路径。例如有如下交通图: 则从A出发到各点的最短路径分别为: B:0 C:10 D:50 E:30 F:60 输…...
基于SSM实现的电动汽车充电网点管理系统
一、系统架构 前端:jsp | jquery | bootstrap | css 后端:spring | springmvc | jdbc 环境:jdk1.8 | mysql 二、代码及数据库 三、功能介绍 01. web端-首页 02. web端-登录 03. web端-注册 04. web端-我要充电 05. web端-个人中心-消…...
Android ImageView如何使用.svg格式图片
我们知道imageview常用的图片格式是.jpg/.png或者drawable里的部分.xml文件。但有时UI会给过来.svg格式的文件,下面讲解如何使用.svg格式图片文件 step1:AS点击File -> New -> Vector Asset step2:选中要使用的.svg文件,按需要命名和调整&#x…...

力扣热题100道-子串篇
字串 560.和为K的子数组 给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的子数组的个数 。 子数组是数组中元素的连续非空序列。 示例 1: 输入:nums [1,1,1], k 2 输出:2示例 2: 输入&a…...

day3--Shell
1.shell语法 概论 概论 shell是我们通过命令行与操作系统沟通的语言。shell脚本可以直接在命令行中执行,也可以将一套逻辑组织成一个文件,方便复用。 AC Terminal中的命令行可以看成是一个“shell脚本在逐行执行”。Linux中常见的shell脚本有很多种&…...

【数据结构】插入排序、选择排序、冒泡排序、希尔排序、堆排序
前言:生活中我们总是会碰到各种各样的排序,今天我们就对部分常用的排序进行总结和学习,今天的内容还是相对比较简单的一部分,各位一起加油哦! 💖 博主CSDN主页:卫卫卫的个人主页 💞 ὄ…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...
