Python解题 - CSDN周赛第33期
本期四道题全考过,题解在网上也都搜得到。。。没有想法,顺手水一份题解吧。
第一题:奇偶排序
给定一个存放整数的数组,重新排列数组使得数组左边为奇数,右边为偶数。
输入描述:第一行输入整数n。(1<=n<=1000)表示数组大小;第二行输入n个整数a.(1<=n<=100)
输出描述:输出重排之后的数组。
示例:
示例 输入 6
3 34 67 89 90 58输出 3 67 89 34 90 58
分析
超级大水题,直接遍历一遍数组,把奇数和偶数分开成两个数组,最后再把两个数组返回即可,时间复杂度 。
如果想加点花,比如降低空间复杂度(上面需要借助外部空间存储奇数和偶数数组),可以在原数组遍历,如果遇到奇数,就和它前面的数交换位置,直到前面为空或不是偶数位置。类似冒泡排序,时间复杂度 ,很没必要。
本题因为要求奇数间和偶数间的相对位置不变,所以不能使用不稳定的排序方法比如快排。
参考代码
n = int(input().strip())
arr = [int(item) for item in input().strip().split()]
odd = list()
even = list()
for i in arr:if i%2: odd.append(i)else: even.append(i)
print(*odd, *even)第二题:小艺改编字符串
已知字符串str。添加至少多少字符可以使得str变成回文串。
输入描述:输入字符串s.(1<=len(str)<=100000)
输出描述:输出最小需要添加字符的数量。
示例:
示例 输入 abab 输出 1
分析
很久以前考过,不过还是值得一说。思路还是动态规划,好像递归也可以?没有试过。
问哥觉得关于字符串的动态规划常常有点抽象,不太好理解,所以保险起见,我们还是画图来看。
首先,对于任意一个长度大于 1 的字符串(长度等于 1 的字符串本身就是回文串,不需要添加字符),如果我们观察它的左右两端,只有下面两种可能:
- 最左端和最右端的字符相同;
- 最左端和最右端的字符不同。
我们可以用 和
表示左右两端字符串的下标,用
表示从下标
到
的字符串,如下图所示:

然后,对于左右端字符相同的字符串,我们可以把它们剥掉,得到一个新的子串 ,很显然,只要子串
是回文串,那么原来的
必定也是回文串。所以原问题就转变成一个子问题:需要添加多少字符可以使得子串
变成回文串?

而对于左右端字符不同的字符串,我们有两种选择:
- 如果子串
是回文串,我们可以在左边添加一个和最右端相同的字符,使原字符串
变成回文串;
- 如果子串
是回文串,则我们也可以在右边添加一个和最左端相同的字符,使原字符串
变成回文串。

那么,只要在这两种选择中取较小的作为答案即可。
于是,动态转移过程就很清楚了。我们定义一个二维数组 表示需要添加多少字符使得字符串
变成回文串,则可得状态转移方程如下(
和
分别表示字符串
左右两端的字符):
- 如果
,则
- 如果
,则
先给个递归的写法,就是直接把上面的转移公式套进来。
参考代码一
def fun(s):n = len(s)if n <= 1: return 0i, j = 0, n-1if s[i] == s[j]: return fun(s[i+1:j])return min(fun(s[i:j]), fun(s[i+1:j+1]))+1
s = input().strip()
print(fun(s))但是因为字符串长度达到1e5,递归极有可能超时。
但是递归给我们的顺序值得参考:所有递归到最终的字符串长度必定为 1 或 0 (空字符串)。
所以,如果我们使用动态规划,原字符串的答案,必须按子字符串的长度,从小到大,递推过来。也就是说,我们必须先得到所有长度为 1 或 0 的子串的答案,再递推到长度为 2 的,然后是长度为 3 的。。。直到长度等于原字符串。
所以我们在传统的 双循环中必须加一个变量
,用来表示子字符串的长度。而一旦
的长度确定了,
,所以还是双循环。循环次数也很好计算,就是所有子串数量之和:
时间复杂度是 ,但是因为除以 2,所以计算量级还是 1e9,勉强可以接受。
参考代码二
s = input().strip()
n = len(s)
dp = [[0]*n for _ in range(n)]
for k in range(1, n):for i in range(n - k):j = i + kif s[i] == s[j]: dp[i][j] = dp[i+1][j-1]else: dp[i][j] = min(dp[i+1][j], dp[i][j-1]) + 1
print(dp[0][n-1])第三题:公司新表
公司里为了凸显公司的特性。安装了一个n进制表。已知新的表的时间是”H:M”。时间合法的定义为H<=23 && M<=59。时间有多少种进制定义的方式,依次打印出来。如果有无数种解输出”-1”,不存在输出”0”。
输入描述:输入一行字符串a:b形式。
输出描述:输出答案。
示例:
示例 输入 11:20 输出 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
分析
13期考过。
不难,但是因为要分析字符串,既抽象又繁琐,所以本题参考代码不想给了,问哥写得很繁琐,大部分时间浪费在这题,看到就烦 ><。
简单说说思路:先把给定的字符串按冒号一分为二,左边为小时数,右边为分钟数。
先特判,什么样的情况是有无数种解呢?因为字符串中可以含有字母,那么假定字母代表了一个数字,只要不进位(字符串长度为 1),就可以代表无数种解。比如一个字母 A,可以代表11进制以上的所有进制,因为 A 就代表了10(按照顺序),是合法的小时(小于24)或分钟(小于60)数。同样,很显然,如果代表小时的一个字母表示了24以上的十进制数字,或代表分钟的一个字母表示60以上的十进制数字,则必定是没有解,返回 0。
而如果进了一位,答案必定有限,比如 11,最多只能代表22进制(该进制中11代表十进制的23)。所以,只要检查分割后的代表小时和分钟的字符串的长度,小于等于1且代表十进制数字小于24或小于60,就必定是无数种解,直接返回-1。
然后就是穷举了,从小时和分钟数所能代表的最小进制开始,比如字符串AB,不可能代表12进制及以下的进制。然后循环加一,每次计算小时和分钟翻译成十进制是否小于24和小于60。知道不满足此条件为止。
如果一个都没找到,很显然,直接返回 0。否则就把所有答案打印出来即可。
第四题:选择客栈
丽江河边有 n 家很有特色的客栈,客栈按照其位置顺序从 1 到 n 编号。每家客栈都按照某一种色调进行装饰(总共 k 种,用整数 0 ~ k-1 表示),且每家客栈都设有一家咖啡店,每家咖啡店均有各自的最低消费。两位游客一起去丽江旅游,他们喜欢相同的色调,又想尝试两个不同的客栈,因此决定分别住在色调相同的两家客栈中。晚上,他们打算选择一家咖啡店喝咖啡,要求咖啡店位于两人住的两家客栈之间(包括他们住的客栈),且咖啡店的最低消费不超过 p 。他们想知道总共有多少种选择住宿的方案,保证晚上可以找到一家最低消费不超过 p 元的咖啡店小聚。
输入描述:共n+1 行。第一行三个整数 n ,k ,p ,每两个整数之间用一个空格隔开,分别表示客栈的个数,色调的数目和能接受的最低消费的最高值;接下来的 n 行,第 i+1 行两个整数,之间用一个空格隔开,分别表示 i 号客栈的装饰色调和 i 号客栈的咖啡店的最低消费。
输出描述:一个整数,表示可选的住宿方案的总数。
示例:
示例 输入 5 2 3
0 5
1 3
0 2
1 4
1 5输出 3
分析
15期考过。还是动态规划,可以参考我以前的题解,详细记录了思考过程(写得可能有些繁琐),这里不再赘述了。
相关文章:
Python解题 - CSDN周赛第33期
本期四道题全考过,题解在网上也都搜得到。。。没有想法,顺手水一份题解吧。 第一题:奇偶排序 给定一个存放整数的数组,重新排列数组使得数组左边为奇数,右边为偶数。 输入描述:第一行输入整数n。(1<n<…...

Session攻击
Session攻击Session攻击简介主要攻击方式会话预测会话劫持中间人攻击会话固定Session攻击简介 Session对于Web应用是最重要的,也是最复杂的。对于Web应用程序来说,加强安全性的首要原则就是:不要信任来自客户端的数据,一定要进行数据验证以及…...
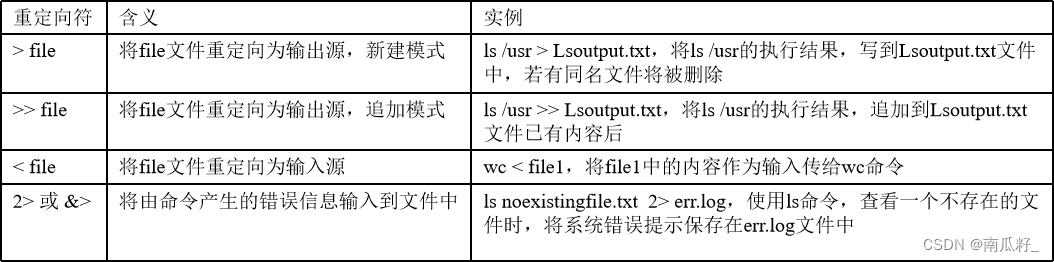
【Linux】Shell详解
😊😊作者简介😊😊 : 大家好,我是南瓜籽,一个在校大二学生,我将会持续分享Java相关知识。 🎉🎉个人主页🎉🎉 : 南瓜籽的主页…...

汉字找不同隐私协议
本隐私信息保护政策版本:2021 V1 一、重要提示 请您(以下亦称“用户”)在使用本平台App时仔细阅读本协议之全部条款,并确认您已完全理解本协议之规定,尤其是涉及您的重大权益及义务的加粗或划线条款。如您对协议有任…...

CEC2017:斑马优化算法(Zebra Optimization Algorithm,ZOA)求解cec2017(提供MATLAB代码)
一、斑马优化算法 斑马优化算法(Zebra Optimization Algorithm,ZOA)Eva Trojovsk等人于2022年提出,其模拟斑马的觅食和对捕食者攻击的防御行为。 斑马因身上有起保护作用的斑纹而得名。没有任何动物比斑马的皮毛更与众不同。斑…...

【Linux要笑着学】进程创建 | 进程终止 | slab分派器
爆笑教程《看表情包学Linux》👈 猛戳订阅!💭 写在前面:本章我们主要讲解进程的创建与终止。首先讲解进程创建,fork 函数是我们早在讲解 "进程的概念" 章节就提到过的一个函数&#…...

数据资产管理建设思考(二)
关于数据资产管理,近两年是数据治理行业中一个热点话题,当然有我们前面提到的国家的政策支持及方向指引的原因。另一方面我们做数据治理的同行们从学习吸收国外优秀的数据治理理论,进一步在实践中思考如何应用理论,并结合我们国家…...

微软发布多模态版ChatGPT!取名“宇宙一代”
文|CoCo酱Ludwig Wittgenstein曾说过:“我语言的局限,即是我世界的局限”。大型语言模型(LLM)已成功地作为各种自然语言任务的通用接口,只要我们能够将输入和输出转换为文本,就可以将基于LLM的接…...
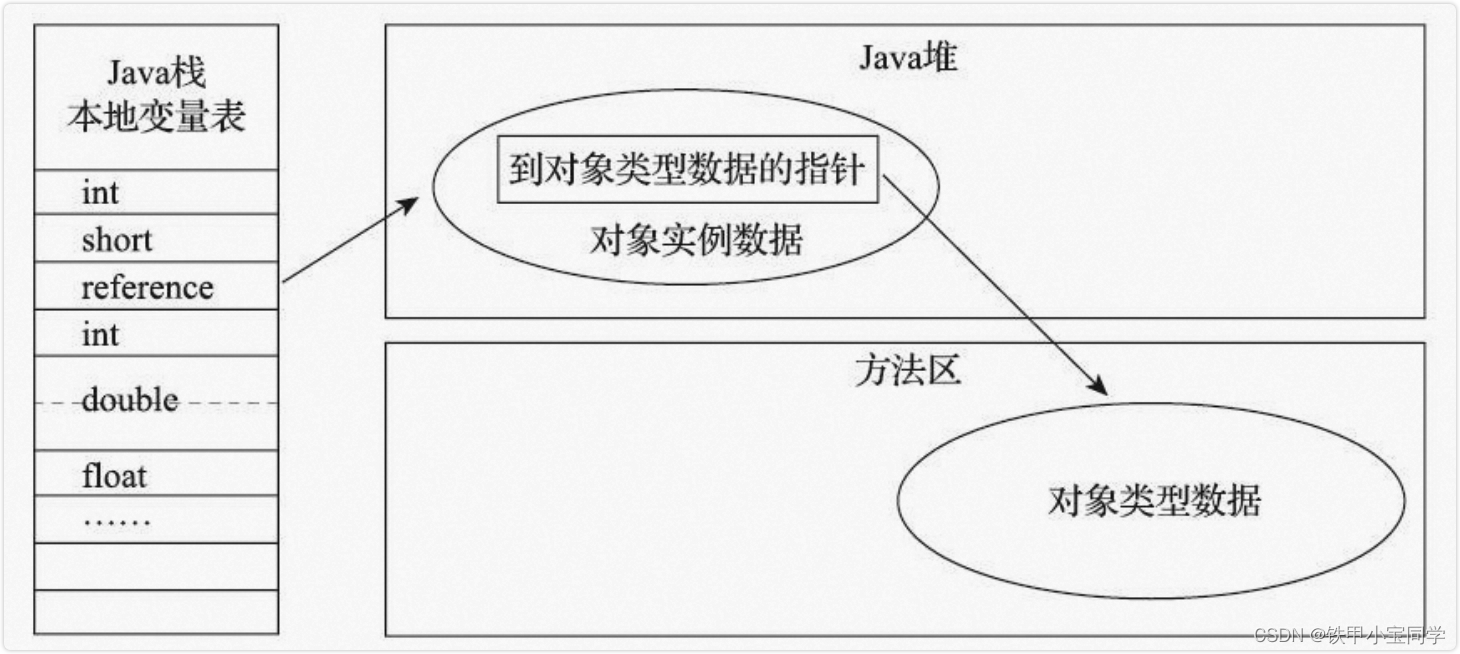
【学习笔记】深入理解JVM之对象的实例化
参考尚硅谷JVM 102 - 106 集 首发地址:地址 1、JVM对象的实例化 1.1 对象的创建方式 对象有一下几种创建对象的方式 new Object object new Object();Class的newInstance() Object object Object.class.newInstance();Constructor的newInstance(…...

IP协议的漏洞及防护措施
文章目录一、TCP/IP协议族二、IP协议三、IP协议的安全问题及防护措施一、TCP/IP协议族 二、IP协议 网际协议(Internet Protocol,IP)是TCP/IP协议族的核心,也是网际层最重要的协议。 IP数据报由首部和数据两部分组成;…...

Linux命令·mkdir
linux mkdir 命令用来创建指定的名称的目录,要求创建目录的用户在当前目录中具有写权限,并且指定的目录名不能是当前目录中已有的目录。1.命令格式:mkdir [选项] 目录...2.命令功能:通过 mkdir 命令可以实现…...

智能家居项目(八)之树莓派+摄像头进行人脸识别
目录 1、编辑Camera.c 2、编辑contrlDevices.h 3、编辑mainPro.c 4、进行编译: 5、运行结果: ./test1 6、项目图片演示 智能家居项目(七)之Libcurl库与HTTPS协议实现人脸识别_Love小羽的博客-CSDN博客 经过上一篇文章&…...

渗透测试之地基服务篇:无线攻防之钓鱼无线攻击(上)
简介 渗透测试-地基篇 该篇章目的是重新牢固地基,加强每日训练操作的笔记,在记录地基笔记中会有很多跳跃性思维的操作和方式方法,望大家能共同加油学到东西。 请注意 : 本文仅用于技术讨论与研究,对于所有笔记中复现…...

「ABAP」一文带你入门OPEN SQL中的SELECT查询(附超详细案例解析)
💂作者简介: THUNDER王,一名热爱财税和SAP ABAP编程以及热爱分享的博主。目前于江西师范大学会计学专业大二本科在读,同时任汉硕云(广东)科技有限公司ABAP开发顾问。在学习工作中,我通常使用偏后…...

【搞透C语言指针】那年我双手插兜, 不知道指针是我的对手
☃️内容专栏:【C语言】进阶部分 ☃️本文概括: 征服C语言指针!一篇文章搞清楚指针的全部要点。 ☃️本文作者:花香碟自来_ ☃️发布时间:2023.3.3 目录 一、字符指针 二、指针数组 三、数组指针 1.数组指针的定义…...
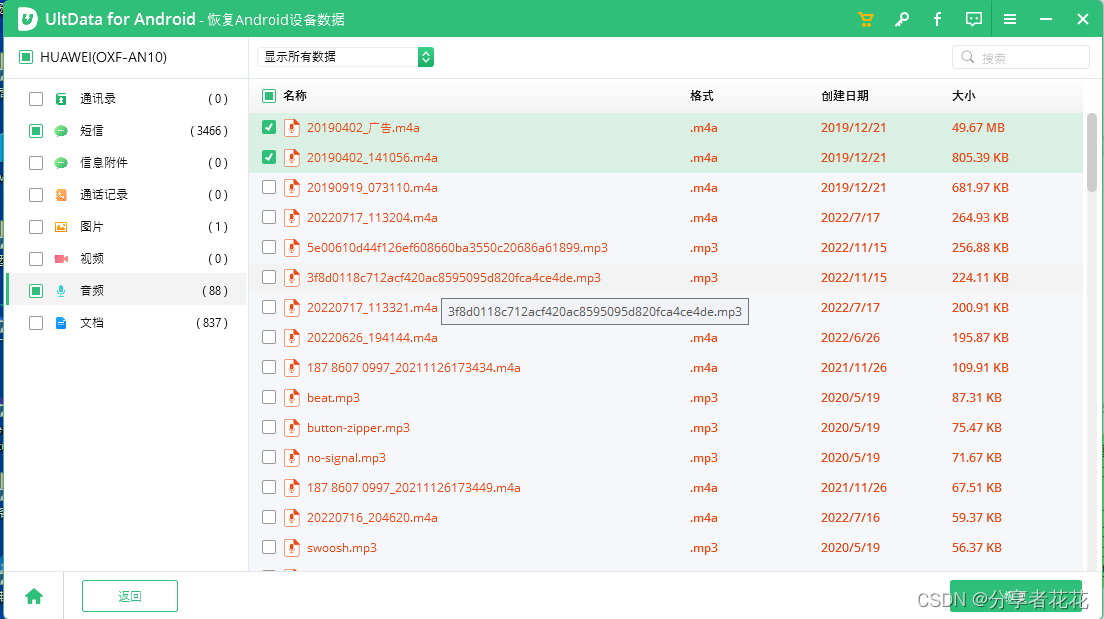
如何从 Android 手机上的 SD 卡恢复已删除的照片
为了扩展手机的存储空间,很多人都会在安卓手机上插入一张SD卡来存储一些大文件,比如电影、照片、视频等。虽然SD卡给我们带来了很大的方便,但我们还是避免不了数据丢失一些事故造成的。您是否正在为 SD 卡上的照片意外丢失而苦恼?…...
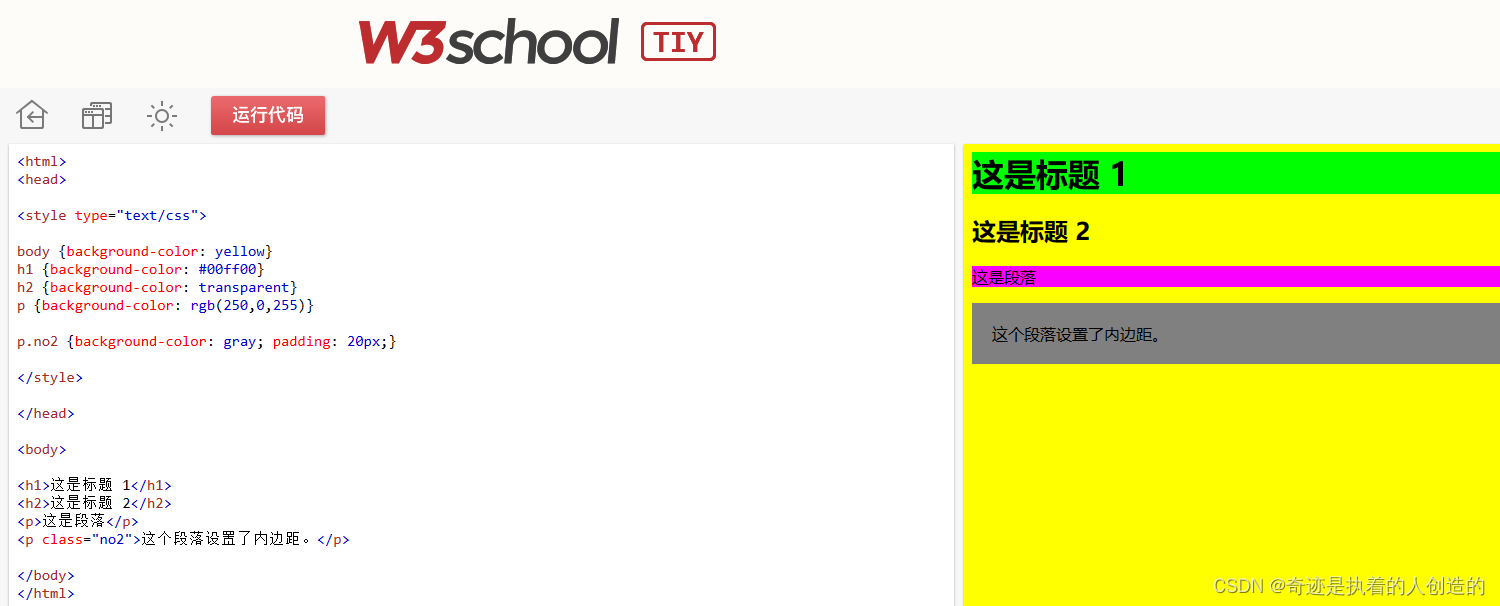
01-前端-htmlcss
文章目录HTML&CSS1,HTML1.1 介绍1.2 快速入门1.3 基础标签1.3.1 标题标签1.3.2 hr标签1.3.3 字体标签1.3.4 换行标签1.3.5 段落标签1.3.6 加粗、斜体、下划线标签1.3.7 居中标签1.3.8 案例1.4 图片、音频、视频标签1.5 超链接标签1.6 列表标签1.7 表格标签1.8 布…...

【YOLO系列】YOLOv5超详细解读(网络详解)
前言 吼吼!终于来到了YOLOv5啦! 首先,一个热知识:YOLOv5没有发表正式论文哦~ 为什么呢?可能YOLOv5项目的作者Glenn Jocher还在吃帽子吧,hh 目录 前言 一、YOLOv5的网络结构 二、输入端 (1…...

从 ChatGPT 爆火回溯 NLP 技术
ChatGPT 火遍了全网,多个话题频频登上热搜。见证了自然语言处理(NLP)技术的重大突破,体验到通用技术的无限魅力。GPT 模型是一种 NLP 模型,使用多层变换器(Transformer)来预测下一个单词的概率分…...

面了 6 家大厂,并拿下 5 家 offer,进大厂好像也没有那么困难吧....
前言 二月份的时候因为换工作的缘故,陆续参加了华为、蚂蚁、字节跳动、PDD、百度、Paypal 的社招面试,除了字节跳动流程较长,我主动结束面试以外,其他的都顺利拿到了 Offer。 最近时间稍微宽裕点了,写个面经…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...
