【机器学习】深度学习概论(二)
五、受限玻尔兹曼机(Restricted Boltzmann Machine,RBM)

5.1 RBM介绍

示例代码:
Python 编写了一个简单的 RBM 实现,并用一些假数据训练了它。然后,他展示了如何用 RBM 来解释用户的电影偏好,以及如何用 RBM 来生成电影推荐:
使用一些假数据训练了RBM。
爱丽丝:(哈利波特 = 1,阿凡达 = 1,LOTR 3 = 1,角斗士 = 0,泰坦尼克号 = 0,闪光 = 0)。SF/奇幻大粉丝。
鲍勃:(哈利波特 = 1,阿凡达 = 0,LOTR 3 = 1,角斗士 = 0,泰坦尼克号 = 0,闪光 = 0)。SF/奇幻迷,但不喜欢《阿凡达》。
卡罗尔:(哈利波特 = 1,阿凡达 = 1,LOTR 3 = 1,角斗士 = 0,泰坦尼克号 = 0,闪光 = 0)。SF/奇幻大粉丝。
大卫:(哈利波特 = 0,阿凡达 = 0,LOTR 3 = 1,角斗士 = 1,泰坦尼克号 = 1,闪光 = 0)。奥斯卡大奖得主的粉丝。
埃里克:(哈利波特 = 0,阿凡达 = 0,LOTR 3 = 1,角斗士 = 1,泰坦尼克号 = 1,闪光 = 0)。奥斯卡奖得主的粉丝,泰坦尼克号除外。
弗雷德:(哈利波特 = 0,阿凡达 = 0,LOTR 3 = 1,角斗士 = 1,泰坦尼克号 = 1,闪光 = 0)。奥斯卡大奖得主的粉丝。
该网络学习了以下权重:
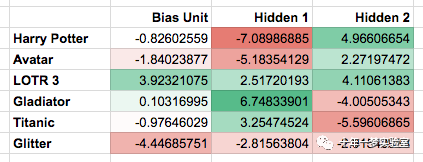
请注意,第一个隐藏单元似乎对应于奥斯卡奖得主,第二个隐藏单元似乎对应于 SF/奇幻电影,正如我们所希望的那样。
如果我们给 RBM 一个新用户 George,他将 (Harry Potter = 0, Avatar = 0, LOTR 3 = 0, Gladiator = 1, Titanic = 1, Glitter = 0) 作为他的偏好,会发生什么?它打开了奥斯卡奖得主单元(但不是 SF/奇幻单元),正确地猜测乔治可能喜欢奥斯卡奖得主的电影。
如果我们只激活 SF/幻想单元,并运行一系列不同的 RBM,会发生什么?在我的试验中,它打开了哈利波特、阿凡达和 LOTR 3 三次;它打开了《阿凡达》和《LOTR 3》,但没有打开《哈利波特》一次;它打开了哈利波特和 LOTR 3,但没有打开阿凡达,两次。请注意,根据我们的训练示例,这些生成的偏好确实符合我们期望真正的 SF/奇幻粉丝想要观看的内容。
# 导入未来模块,用于兼容不同版本的Python
from __future__ import print_function
# 导入numpy库,用于科学计算
import numpy as np# 定义一个类,表示受限玻尔兹曼机
class RBM:# 定义初始化方法,接受可见层单元数和隐藏层单元数作为参数def __init__(self, num_visible, num_hidden):# 将隐藏层单元数和可见层单元数赋值给类的属性self.num_hidden = num_hiddenself.num_visible = num_visible# 设置一个调试打印的标志,用于控制是否打印训练信息self.debug_print = True# 创建一个随机数生成器,指定随机种子为1234np_rng = np.random.RandomState(1234)# 创建一个权重矩阵,用于存储可见层和隐藏层之间的连接权重# 权重矩阵的形状为(num_visible, num_hidden),即每一列对应一个隐藏单元,每一行对应一个可见单元# 权重矩阵的初始值为均匀分布在[-0.1 * np.sqrt(6. / (num_hidden + num_visible)),# 0.1 * np.sqrt(6. / (num_hidden + num_visible))]之间的随机数,这个范围是根据论文中的建议选择的self.weights = np.asarray(np_rng.uniform(low=-0.1 * np.sqrt(6. / (num_hidden + num_visible)),high=0.1 * np.sqrt(6. / (num_hidden + num_visible)),size=(num_visible, num_hidden)))# 在权重矩阵的第一行和第一列插入零,用于表示偏置单元的权重# 偏置单元是一种特殊的单元,它的值始终为1,用于增加模型的灵活性# 第一行的权重表示隐藏层的偏置,第一列的权重表示可见层的偏置self.weights = np.insert(self.weights, 0, 0, axis = 0)self.weights = np.insert(self.weights, 0, 0, axis = 1)# 定义一个训练方法,接受数据,最大训练轮数,学习率等参数def train(self, data, max_epochs = 1000, learning_rate = 0.1):# 获取数据的样本数,即第一个维度的大小num_examples = data.shape[0]# 在数据的第一列插入1,用于表示偏置单元的值data = np.insert(data, 0, 1, axis = 1)# 遍历训练轮数for epoch in range(max_epochs): # 将数据作为可见层的状态,计算隐藏层的激活值# 这是正向传播的过程,也称为正相对比散度阶段,或者现实阶段# 激活值等于数据与权重矩阵的点积,形状为(num_examples, num_hidden + 1)pos_hidden_activations = np.dot(data, self.weights) # 计算隐藏层的激活概率,即隐藏层的单元以一定的概率被激活(取值为1)# 激活概率是通过逻辑斯蒂函数(或称为Sigmoid函数)计算的,它可以将任意值映射到(0,1)之间# 形状仍为(num_examples, num_hidden + 1)pos_hidden_probs = self._logistic(pos_hidden_activations)# 将第一列的激活概率设为1,用于表示偏置单元的值pos_hidden_probs[:,0] = 1 # Fix the bias unit.# 根据隐藏层的激活概率,生成隐藏层的状态# 隐藏层的状态是一个二值的矩阵,形状为(num_examples, num_hidden + 1)# 隐藏层的状态等于激活概率是否大于一个随机数,如果大于则为1,否则为0pos_hidden_states = pos_hidden_probs > np.random.rand(num_examples, self.num_hidden + 1)# 注意,我们在计算关联矩阵时,使用的是隐藏层的激活概率,而不是隐藏层的状态# 我们也可以使用状态,具体可以参考Hinton的论文《A Practical Guide to Training Restricted Boltzmann Machines》的第三节# 关联矩阵是可见层和隐藏层的状态的外积,形状为(num_visible + 1, num_hidden + 1)pos_associations = np.dot(data.T, pos_hidden_probs)# 从隐藏层的状态重构可见层的激活值# 这是反向传播的过程,也称为负相对比散度阶段,或者梦境阶段# 激活值等于隐藏层的状态与权重矩阵的转置的点积,形状为(num_examples, num_visible + 1)neg_visible_activations = np.dot(pos_hidden_states, self.weights.T)# 计算可见层的激活概率,即可见层的单元以一定的概率被激活(取值为1)# 激活概率是通过逻辑斯蒂函数(或称为Sigmoid函数)计算的,它可以将任意值映射到(0,1)之间# 形状仍为(num_examples, num_visible + 1)neg_visible_probs = self._logistic(neg_visible_activations)# 将第一列的激活概率设为1,用于表示偏置单元的值neg_visible_probs[:,0] = 1 # Fix the bias unit.# 从可见层的激活概率计算隐藏层的激活值# 激活值等于可见层的激活概率与权重矩阵的点积,形状为(num_examples, num_hidden + 1)neg_hidden_activations = np.dot(neg_visible_probs, self.weights)# 计算隐藏层的激活概率,即隐藏层的单元以一定的概率被激活(取值为1)# 激活概率是通过逻辑斯蒂函数(或称为Sigmoid函数)计算的,它可以将任意值映射到(0,1)之间# 形状仍为(num_examples, num_hidden + 1)neg_hidden_probs = self._logistic(neg_hidden_activations)# 注意,我们在计算关联矩阵时,使用的是可见层和隐藏层的激活概率,而不是状态# 关联矩阵是可见层和隐藏层的激活概率的外积,形状为(num_visible + 1, num_hidden + 1)neg_associations = np.dot(neg_visible_probs.T, neg_hidden_probs)# 更新权重矩阵# 权重矩阵的更新量等于学习率乘以正相关联矩阵减去负相关联矩阵,再除以样本数# 这样可以使得正相的概率增大,负相的概率减小,从而最大化数据的似然度# 更新权重矩阵,使用学习率、正相联和负相联的差值除以样本数作为增量self.weights += learning_rate * ((pos_associations - neg_associations) / num_examples)# 计算误差,使用数据和负可见概率的差的平方和error = np.sum((data - neg_visible_probs) ** 2)# 如果开启了调试打印,打印出每个迭代的误差if self.debug_print:print("Epoch %s: error is %s" % (epoch, error))# 定义一个方法,用于从可见层运行网络,得到隐藏层的状态def run_visible(self, data):# 获取样本数num_examples = data.shape[0]# 创建一个矩阵,每一行是一个训练样本对应的隐藏单元(加上一个偏置单元)hidden_states = np.ones((num_examples, self.num_hidden + 1))# 在数据的第一列插入偏置单元,值为1data = np.insert(data, 0, 1, axis = 1)# 计算隐藏单元的激活值hidden_activations = np.dot(data, self.weights)# 计算隐藏单元被激活的概率hidden_probs = self._logistic(hidden_activations)# 根据概率随机激活隐藏单元hidden_states[:,:] = hidden_probs > np.random.rand(num_examples, self.num_hidden + 1)# 始终将偏置单元设置为1# hidden_states[:,0] = 1# 忽略偏置单元hidden_states = hidden_states[:,1:]return hidden_states# 定义一个方法,用于从隐藏层运行网络,得到可见层的状态# TODO: 去除这个方法和`run_visible`之间的代码重复?def run_hidden(self, data):# 获取样本数num_examples = data.shape[0]# 创建一个矩阵,每一行是一个训练样本对应的可见单元(加上一个偏置单元)visible_states = np.ones((num_examples, self.num_visible + 1))# 在数据的第一列插入偏置单元,值为1data = np.insert(data, 0, 1, axis = 1)# 计算可见单元的激活值visible_activations = np.dot(data, self.weights.T)# 计算可见单元被激活的概率visible_probs = self._logistic(visible_activations)# 根据概率随机激活可见单元visible_states[:,:] = visible_probs > np.random.rand(num_examples, self.num_visible + 1)# 始终将偏置单元设置为1# visible_states[:,0] = 1# 忽略偏置单元visible_states = visible_states[:,1:]return visible_states# 定义一个方法,用于生成梦境样本,即从网络中随机抽取可见层的状态def daydream(self, num_samples):# 创建一个矩阵,每一行是一个可见单元(加上一个偏置单元)的样本samples = np.ones((num_samples, self.num_visible + 1))# 从均匀分布中取第一个样本samples[0,1:] = np.random.rand(self.num_visible)# 开始交替的吉布斯采样# 注意,我们保持隐藏单元的二进制状态,但是将可见单元作为实数概率# 参见 Hinton 的 "A Practical Guide to Training Restricted Boltzmann Machines" 的第三节# 了解更多原因for i in range(1, num_samples):visible = samples[i-1,:]# 计算隐藏单元的激活值hidden_activations = np.dot(visible, self.weights) # 计算隐藏单元被激活的概率hidden_probs = self._logistic(hidden_activations)# 根据概率随机激活隐藏单元hidden_states = hidden_probs > np.random.rand(self.num_hidden + 1)# 始终将偏置单元设置为1hidden_states[0] = 1# 重新计算可见单元被激活的概率visible_activations = np.dot(hidden_states, self.weights.T)visible_probs = self._logistic(visible_activations)visible_states = visible_probs > np.random.rand(self.num_visible + 1)samples[i,:] = visible_states# 忽略偏置单元(第一列),因为它们总是被设置为1return samples[:,1:] # 判断是否是主模块,如果是,则执行以下代码
if __name__ == '__main__':# 创建一个受限玻尔兹曼机的实例,指定可见层单元数为6,隐藏层单元数为2r = RBM(num_visible = 6, num_hidden = 2)# 创建一个训练数据的数组,每一行是一个样本,每一列是一个特征# 这里的数据是一个二值的矩阵,表示6个特征的存在或缺失training_data = np.array([[1,1,1,0,0,0],[1,0,1,0,0,0],[1,1,1,0,0,0],[0,0,1,1,1,0], [0,0,1,1,0,0],[0,0,1,1,1,0]])# 调用训练方法,指定最大训练轮数为5000r.train(training_data, max_epochs = 5000)# 打印出训练后的权重矩阵print(r.weights)# 创建一个用户数据的数组,表示一个新的样本user = np.array([[0,0,0,1,1,0]])# 打印出从可见层运行网络得到的隐藏层的状态print(r.run_visible(user))输出结果:
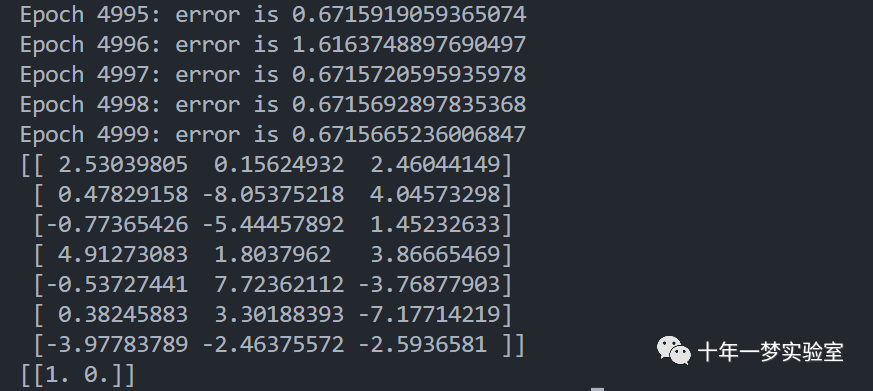
5.2 深度玻尔兹曼机
深度玻尔兹曼机(Deep Boltzmann Machine,DBM)是一种基于能量的生成模型,它可以用来学习复杂数据的概率分布。DBM由多层隐变量组成,每层隐变量之间没有连接,但是每层隐变量都与下一层可见变量或上一层隐变量相连。DBM的最底层是可见层,它表示观测到的数据,例如图像、文本或音频。DBM的目标是最大化数据的对数似然,即让模型生成的数据尽可能接近真实数据。DBM的训练过程涉及到两个阶段:预训练和微调。预训练是使用贪婪逐层算法,将每两层隐变量视为一个受限玻尔兹曼机(Restricted Boltzmann Machine,RBM),并用对比散度(Contrastive Divergence,CD)算法进行无监督学习。微调是使用随机最大似然(Stochastic Maximum Likelihood,SML)算法,对整个模型进行联合优化,以提高模型的泛化能力。
DBM具有以下几个优点:
DBM可以从高维、非线性、非高斯的数据中学习出抽象的特征表示,从而实现数据的降维和特征提取。
DBM可以用于生成新的数据样本,例如生成新的图像或文本,从而实现数据的增强和创造。
DBM可以用于多种任务,例如分类、回归、聚类、协同过滤、推荐系统等,只需在模型的顶层添加一个适当的输出层即可。
DBM也有以下几个缺点:
DBM的训练过程比较复杂和耗时,需要大量的计算资源和数据量。
DBM的训练过程涉及到很多超参数的选择,例如学习率、批量大小、采样步数、正则化项等,这些超参数对模型的性能有很大的影响,但是很难确定最优的值。
DBM的理论分析比较困难,很多性质和定理还没有得到严格的证明,例如模型的收敛性、稳定性、可解释性等
5.3 深度置信网
深度置信网(Deep Belief Network,DBN)是一种基于图模型的生成模型,它由多层受限玻尔兹曼机(RBM)堆叠而成。DBN的最底层是可见层,它表示观测到的数据,例如图像、文本或音频。DBN的最顶层是一个无向图,它表示数据的高层抽象特征。DBN的中间层是有向图,它表示数据的中间层特征。DBN的目标是最大化数据的对数似然,即让模型生成的数据尽可能接近真实数据。DBN的训练过程涉及到两个阶段:预训练和微调。预训练是使用贪婪逐层算法,将每两层视为一个RBM,并用CD算法进行无监督学习。微调是使用反向传播(Backpropagation,BP)算法,对整个模型进行有监督学习,以提高模型的泛化能力。
DBN具有以下几个优点:
DBN可以从高维、非线性、非高斯的数据中学习出抽象的特征表示,从而实现数据的降维和特征提取。
DBN可以用于生成新的数据样本,例如生成新的图像或文本,从而实现数据的增强和创造。
DBN可以用于多种任务,例如分类、回归、聚类、协同过滤、推荐系统等,只需在模型的顶层添加一个适当的输出层即可。
DBN也有以下几个缺点:
DBN的训练过程比较复杂和耗时,需要大量的计算资源和数据量。
DBN的训练过程涉及到很多超参数的选择,例如学习率、批量大小、采样步数、正则化项等,这些超参数对模型的性能有很大的影响,但是很难确定最优的值。
DBN的理论分析比较困难,很多性质和定理还没有得到严格的证明,例如模型的收敛性、稳定性、可解释性等
附录:
受限玻尔兹曼机应用场景

各种激活函数的优缺点
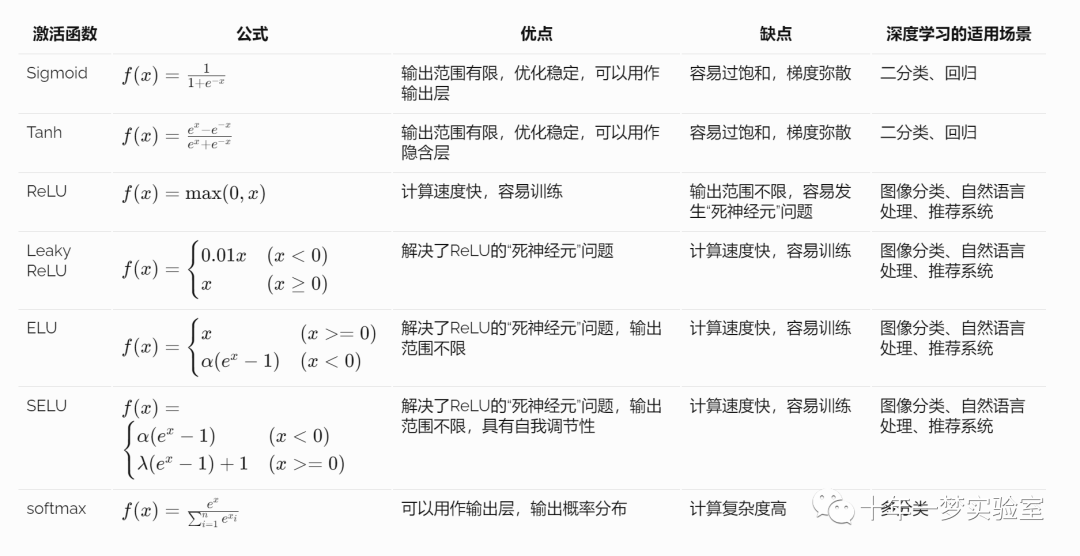
各种激活函数各有优缺点,在深度学习中都有其适用场景。
Sigmoid和Tanh函数是传统的激活函数,具有输出范围有限、优化稳定等优点,但容易过饱和,梯度弥散。
ReLU函数是近年来流行的激活函数,具有计算速度快、容易训练等优点,但容易发生“死神经元”问题。
Leaky ReLU、ELU和SELU等函数是ReLU函数的改进版本,解决了“死神经元”问题。
softmax函数常用于多分类任务,可以用来输出概率分布
参考网址
https://blog.echen.me/2011/07/18/introduction-to-restricted-boltzmann-machines/
https://github.com/python-pillow/Pillow/ Python 图像库
https://blog.echen.me/2011/07/18/introduction-to-restricted-boltzmann-machines/ 受限玻尔兹曼机简介 (echen.me)
The End
相关文章:

【机器学习】深度学习概论(二)
五、受限玻尔兹曼机(Restricted Boltzmann Machine,RBM) 5.1 RBM介绍 示例代码: Python 编写了一个简单的 RBM 实现,并用一些假数据训练了它。然后,他展示了如何用 RBM 来解释用户的电影偏好,以…...
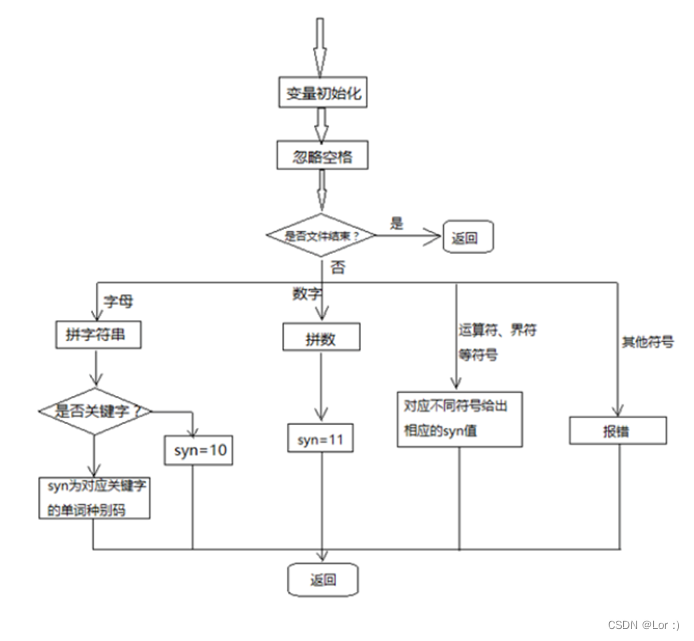
词法语法语义分析程序设计及实现,包含出错提示和错误恢复
词法说明 (1)关键字 main, int, char, if, else, for, while, void (2)运算符 - * / < < > > ! (3)界符 ; ( ) { } (4)标识符 ID letter(letter|digit)* (5)整型常数 NUM digit digit* (6)空格 ‘ ‘ ‘\n’ ‘\r’ ‘\t’ 空格用来分隔ID,NUM,运算符,界…...

Linux的capability深入分析
from:https://www.cnblogs.com/iamfy/archive/2012/09/20/2694977.html 一)概述: 1)从2.1版开始,Linux内核有了能力(capability)的概念,即它打破了UNIX/LINUX操作系统中超级用户/普通用户的概念,由普通用户也可以做只有超级用户可以完成的工作. 2)capability可以作用在进程上…...

【自然语言处理】类似GPT的模型
除了GPT (Generative Pre-trained Transformer) 之外,还有一些其他的好用的类似工具可以用来生成文本。以下是几个受欢迎的工具: BERT (Bidirectional Encoder Representations from Transformers): BERT 是一个预训练的深度双向 Transformer 模型&#…...
【Unity】【FBX】如何将FBX模型导入Unity
【背景】 网上能够找到不少不错的FBX模型资源,大大加速游戏开发时间。如何将这些FBX导入Unity呢? 【步骤】 打开Unity项目文件,进入场景。 点击Projects面板,右键选择Import New Assets 选中FBX文件后导入。Assets文件夹中就会…...
腾讯云标准型S5服务器4核8G配置优惠价格表
腾讯云4核8G服务器S5和轻量应用服务器优惠价格表,轻量应用服务器和CVM云服务器均有活动,云服务器CVM标准型S5实例4核8G配置价格15个月1437.3元,5年6490.44元,轻量应用服务器4核8G12M带宽一年446元、529元15个月,腾讯云…...
学习笔记:R语言基础
文章目录 一、R语言简介二、选择R的原因三、R基本数据对象(一)向量(二)矩阵(三)数组(四)因子(五)列表(六)数据框(七&#…...

初识智慧城市
文章目录 智慧家居 智慧社区 智慧交通 智慧医疗 智慧教育 智慧旅游 智慧农业 智慧安防 智慧家居 利用智能语音、智能交互等技术,实现用户对家居系统各设备的远程操控和能控制如开关窗帘(窗户)、操控家用电器和照明系统、打扫卫生等操作。利用计算机视觉等技术,对被照看…...

Zookeeper之手写一个分布式锁
前言 我之前写了一篇快速上手ZK的文章:https://blog.csdn.net/qq_38974073/article/details/135293106 本篇最要是进一步加深学习ZK,算是一次简单的实践,巩固学习成果。 设计一个分布式锁 对锁的基本要求 可重入:允许同一个应…...
【音视频 ffmpeg 学习】 RTMP推流 mp4文件
1.RTMP(实时消息传输协议)是Adobe 公司开发的一个基于TCP的应用层协议。 2.RTMP协议中基本的数据单元称为消息(Message)。 3.当RTMP协议在互联网中传输数据的时候,消息会被拆分成更小的单元,称为消息块(Chunkÿ…...

跨进程通信 macOS XPC 创建实例
一:简介 XPC 是 macOS 里苹果官方比较推荐和安全的的进程间通信机制。 集成流程简单,但是比较绕。 主要需要集成 XPC Server 这个模块,这个模块最终会被 apple 的根进程 launchd 管理和以独立进程的方法唤起和关闭, 我们主app 进…...

Python圣诞树代码
Python圣诞树代码 # 小黄 2023/12/25import turtle as t # as就是取个别名,后续调用的t都是turtle from turtle import * import random as rn 100.0speed(20) # 定义速度 pensize(5) # 画笔宽度 screensize(800, 800, bgblack) # 定义背景颜色,可…...
flask之文件管理系统-项目 JRP上线啦!!! ---修订版,兼容Windows和Linux系统
上一章的版本https://blog.csdn.net/weixin_44517278/article/details/135275066,在Windows下debug完成无异常后,上传到我的树莓下开始正式服役 由于开发环境是Windows,使用环境是Linux,导致最后没能成功运行起来 这个版本是今天去…...

希尔排序:排序算法中的调优大师
希尔排序:排序算法中的调优大师 大家好,我是免费搭建查券返利机器人赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天,让我们一同探讨一个经典而高效的排序算法——希尔排序。…...

LeetCode 1185. 一周中的第几天
一、题目 1、题目描述 给你一个日期,请你设计一个算法来判断它是对应一周中的哪一天。 输入为三个整数:day、month 和 year,分别表示日、月、年。 您返回的结果必须是这几个值中的一个 {"Sunday", "Monday", "Tues…...
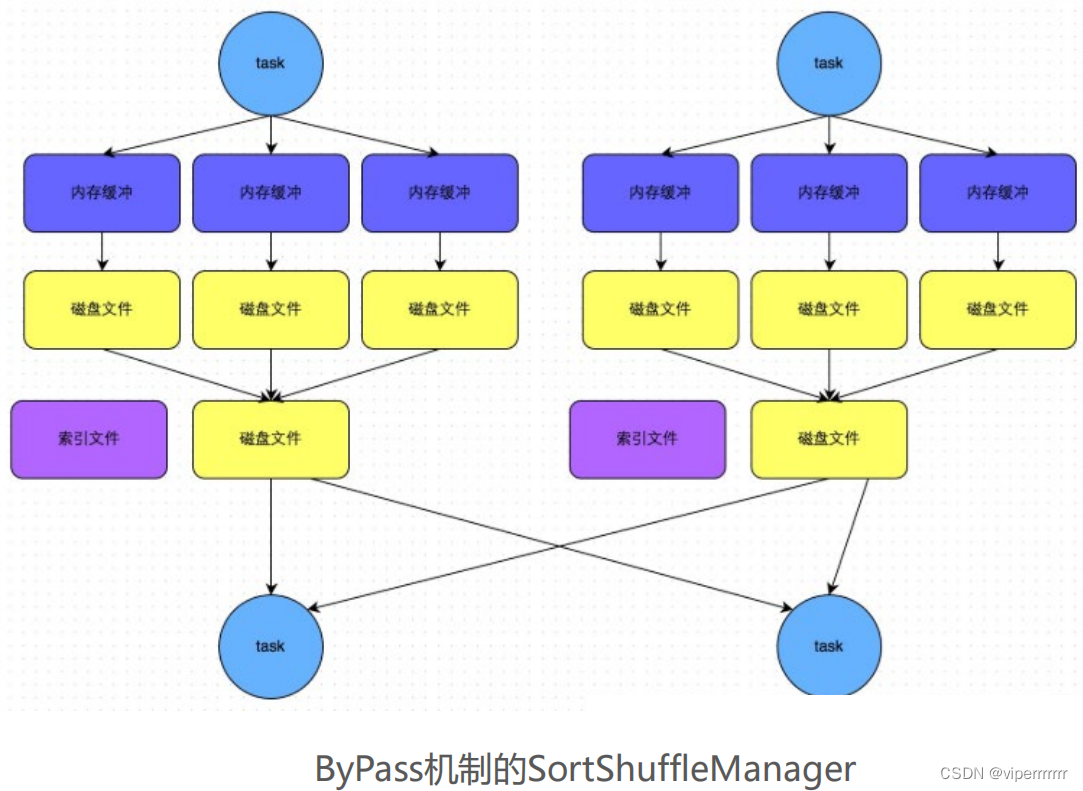
大数据学习(30)-Spark Shuffle
&&大数据学习&& 🔥系列专栏: 👑哲学语录: 承认自己的无知,乃是开启智慧的大门 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言📝支持一下博主哦ᾑ…...

Linux部署ELK
大家好,我是升仔 引言 在复杂的系统架构中,日志管理是一个关键的环节。ELK栈提供了一个高效的解决方案,能够帮助我们快速定位问题、分析数据,并实现实时监控。部署ELK栈是一项挑战,但收益巨大。 基础安装和配置 环境准…...

Python 实现 PDF 到 Word 文档的高效转换(DOC、DOCX)
PDF(Portable Document Format)已成为一种广泛使用的电子文档格式。PDF的主要优势是跨平台,可以在不同设备上呈现一致的外观。然而,当我们需要对文件内容进行编辑或修改,直接编辑PDF文件会非常困难,而且效果…...
【MYSQL】MYSQL 的学习教程(七)之 慢 SQL 优化思路
1. 慢 SQL 优化思路 慢查询日志记录慢 SQLexplain 分析 SQL 的执行计划profile 分析执行耗时Optimizer Trace 分析详情确定问题并采用相应的措施 1. 慢查询日志记录慢 SQL 如何定位慢SQL呢? 我们可以通过 慢查询日志 来查看慢 SQL。 ①:开启慢查询日志…...
unity学习笔记----游戏练习0
一、修复植物种植的问题 1.当手上存在植物时,再次点击卡片上的植物就会在手上添加新的植物,需要修改成只有手上没有植物时才能再次获取到植物。需要修改AddPlant方法。 public bool AddPlant(PlantType plantType) { //防止手上出现多个植…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...
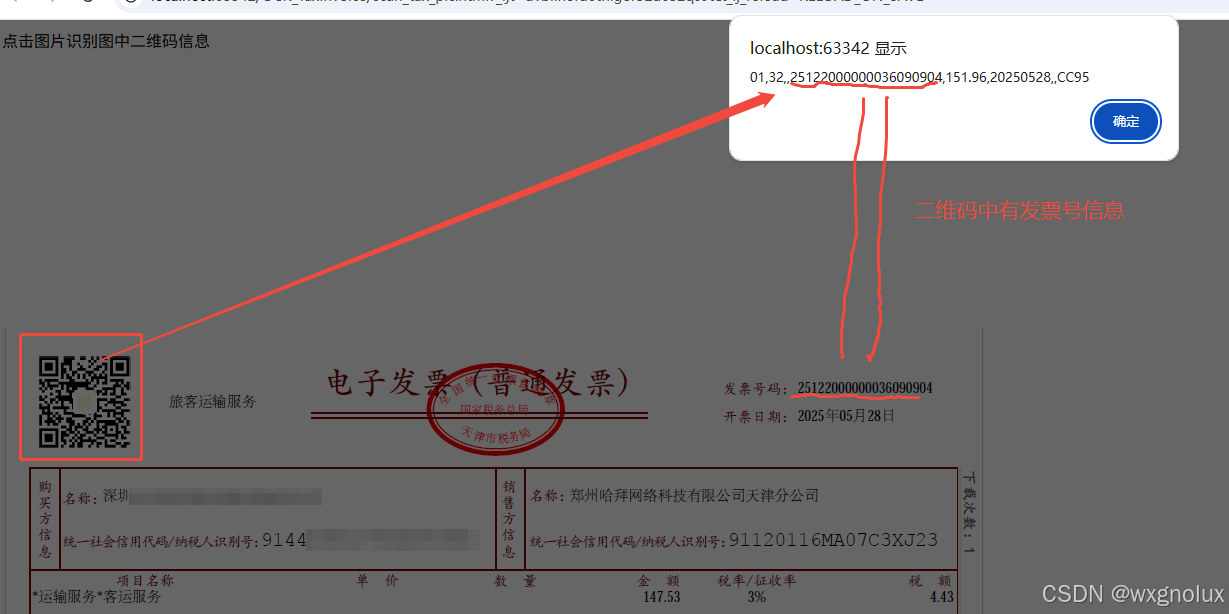
网页端 js 读取发票里的二维码信息(图片和PDF格式)
起因 为了实现在报销流程中,发票不能重用的限制,发票上传后,希望能读出发票号,并记录发票号已用,下次不再可用于报销。 基于上面的需求,研究了OCR 的方式和读PDF的方式,实际是可行的ÿ…...

GeoServer发布PostgreSQL图层后WFS查询无主键字段
在使用 GeoServer(版本 2.22.2) 发布 PostgreSQL(PostGIS)中的表为地图服务时,常常会遇到一个小问题: WFS 查询中,主键字段(如 id)莫名其妙地消失了! 即使你在…...
