【数值分析】乘幂法,matlab实现
乘幂法
一种求实矩阵 A {A} A 的按模最大的特征值,及其对应的特征向量 x i {x_i} xi 的方法,只能求一个。特别适合于大型稀疏矩阵。
一个矩阵的特征值和特征向量可以通过矩阵不断乘以一个初始向量得到。
每次乘完之后要规范化,防止上溢或下溢。规范化可以用各种范数。
要保证矩阵最大特征值只有一个,有 n {n} n 个线性无关的特征向量。
有多个相同特征值时,求得的特征向量可以近似看成排第一个的最大特征值的特征向量。
步骤:
1. 求初始向量 u 0 模最大元素的编号 i d , 初始特征值 β 0 = u 0 ( i d ) , 求归一化后的初始向量 y 0 2. 迭代 , k = 0 , 1 , ⋯ u k + 1 = A y k β k + 1 = u k + 1 ( i d k ) y k + 1 = u k + 1 ∣ ∣ u k + 1 ∣ ∣ ∞ i d k + 1 = u k + 1 模最大元素的编号 3. 判断是否满足 β k + 1 − β k < eps , 特征值 = β k + 1 \begin{align*}1. &求初始向量u_0模最大元素的编号 id \,\,,\,\, 初始特征值 \beta_0=u_0(id) \,\,,\,\, 求归一化后的初始向量y_0 \\ \\ 2.& 迭代 \,\,,\,\, k=0,1, \cdots \\ \\ & u_{k+1}=Ay_k \\ \\ & \beta_{k+1}=u_{k+1}(id_k) \\ \\ & y_{k+1}= \frac{u_{k+1}}{||u_{k+1}||_\infty} \\ \\ & id_{k+1}=u_{k+1}模最大元素的编号 \\ \\ 3.& 判断是否满足 \,\,\, \beta_{k+1}- \beta_k< \text{eps} \,\,,\,\, 特征值= \beta_{k+1} \end{align*} 1.2.3.求初始向量u0模最大元素的编号id,初始特征值β0=u0(id),求归一化后的初始向量y0迭代,k=0,1,⋯uk+1=Aykβk+1=uk+1(idk)yk+1=∣∣uk+1∣∣∞uk+1idk+1=uk+1模最大元素的编号判断是否满足βk+1−βk<eps,特征值=βk+1
[!example]-
A = [ 1 2 1 3 ] , u 0 = [ 0.6 0.8 ] A= \begin{bmatrix} 1 & 2 \\ 1 & 3 \end{bmatrix} \,\,,\,\, u_0= \begin{bmatrix} 0.6\\0.8 \end{bmatrix} A=[1123],u0=[0.60.8]
解:
y 0 = u 0 ∣ ∣ u 0 ∣ ∣ ∞ = [ 0.75 1.00 ] y_0= \frac{u_0}{||u_0||_\infty}= \begin{bmatrix} 0.75\\ 1.00 \end{bmatrix} y0=∣∣u0∣∣∞u0=[0.751.00]
u 1 = A y 0 = [ 2.75 3.75 ] u_1=Ay_0 = \begin{bmatrix} 2.75\\3.75 \end{bmatrix} u1=Ay0=[2.753.75]
在 y 0 {y_0} y0 中 1 {1} 1 在下面,所以近似最大特征值
β 1 = 3.75 \beta_1= 3.75 β1=3.75
特征向量
y 1 = u 1 ∣ ∣ u 1 ∣ ∣ ∞ = [ 0.7333 1.0000 ] y_1= \frac{u_1}{||u_1||_\infty}= \begin{bmatrix} 0.7333\\ 1.0000 \end{bmatrix} y1=∣∣u1∣∣∞u1=[0.73331.0000]
乘幂法matlab实现
%% 乘幂法例子
A = [12 6 -6; 6 16 2; -6 2 16];
u0 = [1.0, 0.5, -0.5]';
format long
[beta1, i] = powerMethod(A, u0, 1e-6, 10)%% 乘幂法求模最大特征值和特征向量
% 输入矩阵、初始迭代向量、精度、最大迭代次数
% 输出特征值、无穷范数归一化后的特征向量、迭代次数
function [lbd, y1, i] = powerMethod(A, u0, eps, max_iter)[u0norm, id] = max(abs(u0)); % 取无穷范数和其所在行beta0 = u0(id);y0 = u0/ u0norm;for i = 1:max_iteru1 = A*y0;beta1 = u1(id);[u1norm, id] = max(abs(u1));y1 = u1/u1norm;if abs(beta1 - beta0)<epslbd = beta1;break;endy0 = y1; % 当前变成过去beta0 = beta1;end
end
相关文章:

【数值分析】乘幂法,matlab实现
乘幂法 一种求实矩阵 A {A} A 的按模最大的特征值,及其对应的特征向量 x i {x_i} xi 的方法,只能求一个。特别适合于大型稀疏矩阵。 一个矩阵的特征值和特征向量可以通过矩阵不断乘以一个初始向量得到。 每次乘完之后要规范化,防止上溢或…...

视频监控EasyCVR如何通过设置sei接口,实现在webrtc视频流中添加画框和文字?
安防视频监控系统基于视频综合管理平台EasyCVR视频系统,采用了开放式的网络结构,可以提供实时远程视频监控、视频录像、录像回放与存储、告警、语音对讲、云台控制、平台级联、磁盘阵列存储、视频集中存储、云存储等丰富的视频能力,具备权限管…...

智能三维数据虚拟现实电子沙盘
一、概述 易图讯科技(www.3dgis.top)以大数据、云计算、虚拟现实、物联网、AI等先进技术为支撑,支持高清卫星影像、DEM高程数据、矢量数据、无人机倾斜摄像、BIM模型、点云、城市白模、等高线、标高点等数据融合和切换,智能三维数…...

【SpringCloud】-GateWay源码解析
GateWay系列 【SpringCloud】-GateWay网关 一、背景介绍 当一个请求来到 Spring Cloud Gateway 之后,会经过一系列的处理流程,其中涉及到路由的匹配、过滤器链的执行等步骤。今天我们来说说请求经过 Gateway 的主要执行流程和原理是什么吧 二、正文 …...
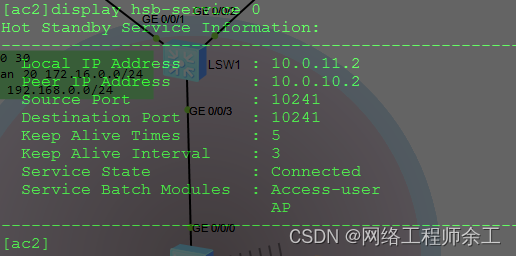
华为无线ac双链路冷备和热备配置案例
所谓的冷备和热备,冷备就是不用vrrp和hsb协议同步ap和用户信息,主的断了等七十五秒后,备的capwap和ap连接上去。 双链路冷备不用vrrp和hsb 双链路热备份只用hsb同步ap和用户信息,不用vrrp,两个ac可以不用在同一个二层…...
VSCode Python开发环境配置
目录 1 插件安装2 Debug和测试配置常见问题 1 插件安装 1.1 基础编译插件,Python、Pylance 1.2 修改语言服务器类型,进入用户配置页面搜索Python: Language Server,选择Pylance(一定要修改可以提供很多语法提示) 1…...

浅谈【GPU和CPU】
GPU和显卡的区别 GPU(Graphics Processing Unit,图形处理器)通常指的就是显卡。显卡是一种安装在计算机中的扩展卡,主要用于图形和图像处理任务。 GPU作为显卡的核心组件,负责处理图形渲染、图像处理、视频解码和其他…...
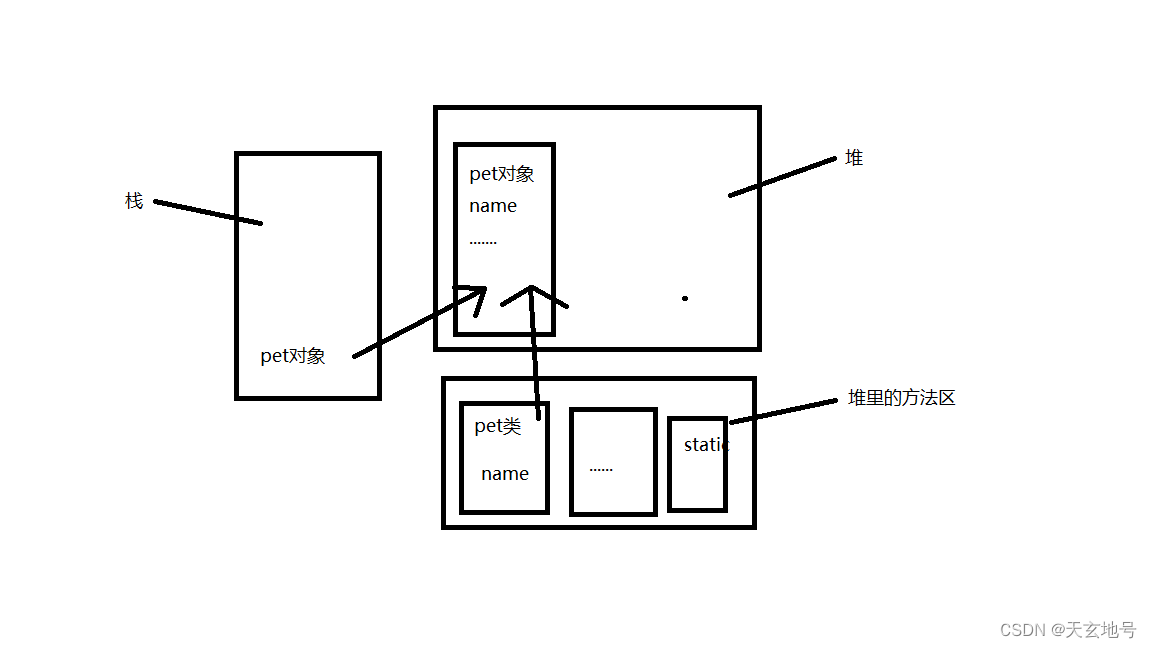
啥是构造器?
当我们new一个对象时就是在引用构造器 构造器又叫做构造函数 构造函数一般分为无参构造函数与有参构造函数 假设我们创建一个pet类,这个类里面就会有一个看不见的自动生成的无参构造函数 如果pet类里没有这个隐形的无参构造,我们new一个对象时就会报错…...

Linux基础知识学习2
tree命令的使用 可以看到dir2目录下的这些文件,要想显示dir2的具体结构,可用tree命令 mv命令 它可以实现两个功能 1.将文件移动到另一个目录中 2.对某一个文件进行重命名 1.将文件移动到另一个目录中 这里将dir1中的2.txt移动到他的子目录dir3中 执行…...

Grafana二进制部署并配置prometheus数据源
1、获取grafna二进制安装包 https://grafana.com/grafana/download?pggraf&plcmtdeploy-box-1 grafana官网下载地址 [rootambari-hadoop1 ~]# cd /opt/module/grafana/ [rootambari-hadoop1 grafana]# pwd /opt/module/grafana2、在安装自己的安装目录执行 wget https:…...

时序预测 | Matlab实现SSA-CNN-BiLSTM麻雀算法优化卷积双向长短期记忆神经网络时间序列预测
时序预测 | Matlab实现SSA-CNN-BiLSTM麻雀算法优化卷积双向长短期记忆神经网络时间序列预测 目录 时序预测 | Matlab实现SSA-CNN-BiLSTM麻雀算法优化卷积双向长短期记忆神经网络时间序列预测预测效果基本介绍程序设计参考资料 预测效果 基本介绍 MATLAB实现SSA-CNN-BiLSTM麻雀算…...

Java中的单元测试
单元测试 单元测试概述: 单元测试是指在软件开发中对软件的最小可测试单元进行测试和验证的过程。最小可测试单元通常是指函数、方法或者类,单元测试可以保证开发人员的代码正确性,同时也方便后期维护和修改。单元测试的主要目的是检测代码的正确性&am…...
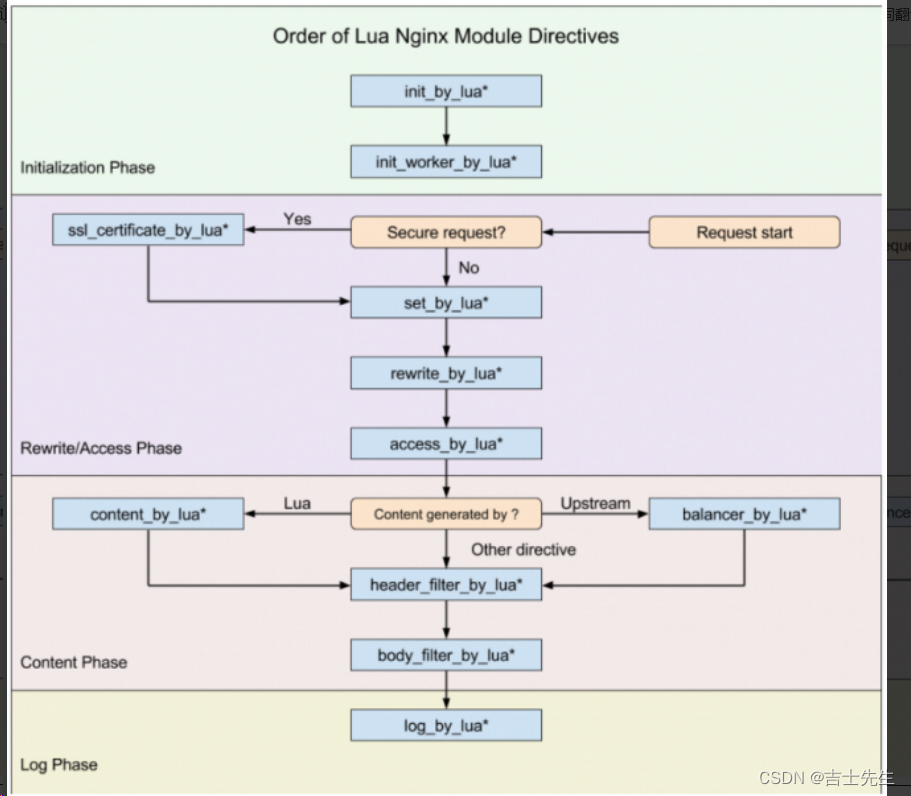
143.【Nginx-02】
Nginx-02 (五)、Nginx负载均衡1.负载均衡概述2.负载均衡的原理及处理流程(1).负载均衡的作用 3.负载均衡常用的处理方式(1).用户手动选择(2).DNS轮询方式(3).四/七层负载均衡(4).Nginx七层负载均衡指令 ⭐(5).Nginx七层负载均衡的实现流程 ⭐ 4.负载均衡状态(1).down (停用)(2)…...

代码随想录刷题 | Day2
今日学习目标 一、基础 链表 接下来说一说链表的定义。 链表节点的定义,很多同学在面试的时候都写不好。 这是因为平时在刷leetcode的时候,链表的节点都默认定义好了,直接用就行了,所以同学们都没有注意到链表的节点是如何定…...

C++ enum class 如何使用
enum class 是 C11 引入的一种新的枚举类型,它是对传统 C 风格的枚举的一种改进。enum class 提供了更强大的类型安全性和作用域限定。以下是关于 enum class 的详细介绍和用法说明: 1. 基本语法 enum class EnumName {Enumerator1,Enumerator2,// ...…...
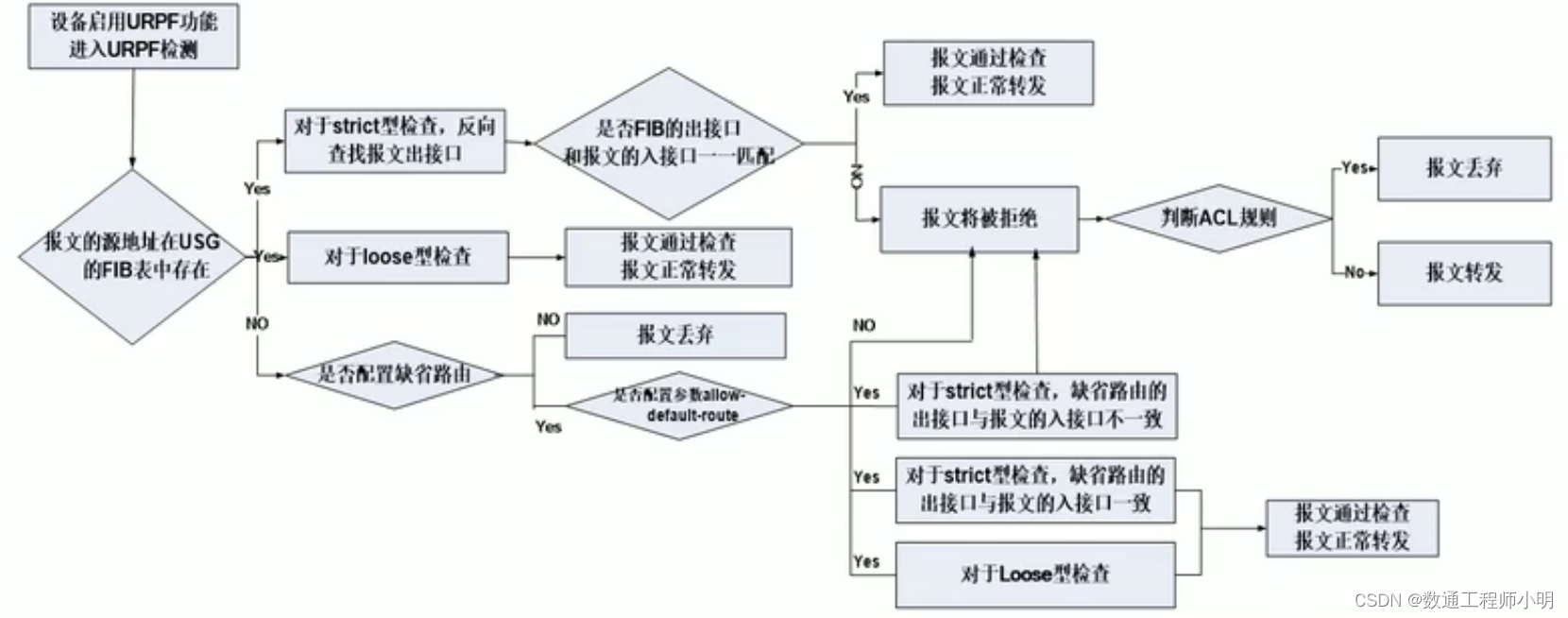
攻防技术-单包攻击防范:扫描、畸形、特殊(HCIP)
单包攻击类型介绍 一、扫描窥探攻击 1、地址扫描攻击防范 攻击介绍 运用ping程序探测目标地址,确定目标系统是否存活。也可使用TCP/UDP报文对目标系统发起探测(如TCP ping)。 防御方法 检测进入防火墙的ICMP、TCP和UDP报文,根…...
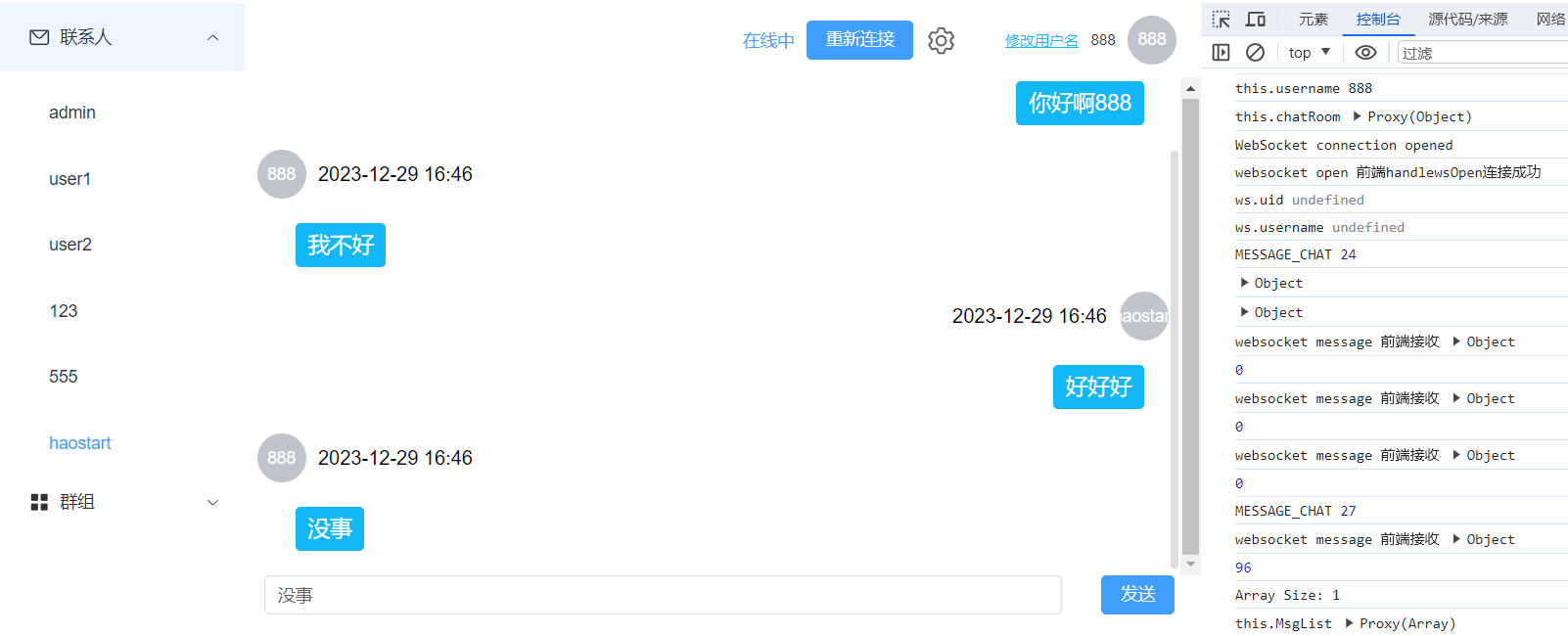
基于 Vue3 和 WebSocket 实现的简单网页聊天应用
首先附上项目介绍,后面详细解释技术细节 1. chat-websocket 一个基于Vue3和WebSocket的简易网络聊天室项目,包括服务端和客户端部分。 项目地址 websocket-chat 下面是项目的主要组成部分和功能: 项目结构 chat-websocket/ |-- server/ # WebSocket 服…...
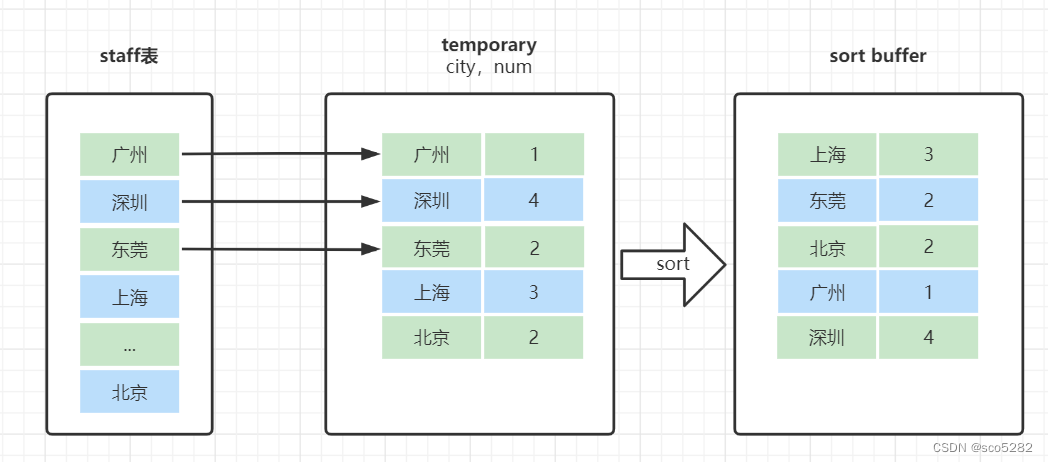
【MYSQL】MYSQL 的学习教程(八)之 12 种慢 SQL 查询原因
日常开发中,我们经常会遇到数据库慢查询。那么导致数据慢查询都有哪些常见的原因呢?今天就跟大家聊聊导致 MySQL 慢查询的 12 个常见原因,以及对应的解决方法: SQL 没加索引SQL 索引失效limit 深分页问题单表数据量太大join 或者…...

C语言例题3
1.设x、y、z和k都是int型变量,则执行表达式:x(y4,z16,k32)后,x的值为(32); x(y4,z16,k32),x的值为32 理解逗号运算符在c语言中的工作方式:逗号运算…...

很实用的ChatGPT网站——httpchat-zh.com
很实用的ChatGPT网站——http://chat-zh.com/ 今天介绍一个好兄弟开发的ChatGPT网站,网址[http://chat-zh.com/]。这个网站功能模块很多,包含生活、美食、学习、医疗、法律、经济等很多方面。下面简单介绍一些部分功能与大家一起分享。 登录和注册页面…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...
