湘潭大学-2023年下学期-c语言-作业0x0a-综合1
A 求最小公倍数
#include<stdio.h>int gcd(int a,int b)
{return b>0?gcd(b,a%b):a;
}int main()
{int a,b;while(~scanf("%d%d",&a,&b)){if(a==0&&b==0) break;printf("%d\n",a*b/gcd(a,b));}return 0;
}
记住最大公约数的函数,然后最小公倍数等于两个数的乘积除以最大公约数,最大公约数函数是代码中的gcd函数
B 爱你一生一世
#include<stdio.h>int gcd(int a,int b)
{return b>0?gcd(b,a%b):a;
}int main()
{int k;scanf("%d",&k);while(k--){int n,m;scanf("%d%d",&n,&m);//礼物的件数和不喜欢的礼物的件数if(m<2) printf("1\n");else if(n==m) printf("0\n");else{int a=(n-1)*n-(m-1)*m;int b=n*(n-1);int temp=gcd(a,b);a/=temp;b/=temp;printf("%d/%d\n",a,b);}}return 0;
}
这道题我非常感慨,因为以前对我来说确实是拦路虎,现在确实可以轻松写出来了
应用最大公约数函数,分式计算的话,就是分子分母同时除以最大公约数,如果分母等于1 ,就只需要输出分子
该题还需要推一下公式,选两件不同的礼物,至少有一件礼物是她喜欢的,反面是没有一件礼物是她喜欢的,用1减去反面的概率,就是我们要求的概率,很明显,反面的概率更容易求

公式如上,不喜欢的礼物数目小于2的话,选两件礼物,一定至少有一件礼物是她喜欢的,所以概率是1,如果所有礼物她都不喜欢,概率就是0(想起来,网上一个段子,她不是不喜欢这件礼物,只是不喜欢你哈哈)
甚至都不需要判断分母是否等于1,因为分母不可能等于1,如果分母等于1,只有一种情况,就是答案为1,但是答案为1的情况我们已经特判过了
C 奇偶校验
#include<stdio.h>
#include<string.h>int main()
{int n;while(~scanf("%d",&n)){if(n==-1) break;int a[10];for(int i=1;i<=8;i++){a[i]=n%2;n/=2;}//for(int i=8;i>=1;i--) printf("%d",a[i]);int cnt=0;for(int i=8;i>=2;i--){if(a[i]==1){cnt++;}}int b=0;if(cnt%2==0) b=0;else b=1;if(b==a[1]) printf("Yes");else printf("No");printf("\n");memset(a,0,sizeof a);}return 0;
}
进制转换的一道题目,对进制取模,然后除以进制,非常经典,记住这个讨论即可
注意这里下标是从0开始的(题干里面),所以我一开始还是非常奇怪的,为什么只算前面六位当数据位,原来从0开始数数到六是七位
思路就是把一个十进制数字转换成二进制数字,把每一位数字存在数组里面,然后根据题目要求模拟一下即可
D n!进制
#include<stdio.h>int a[15];void fact()
{a[0]=1;a[1]=1;for(int i=2;i<=15;i++) a[i]=a[i-1]*i;
}int main()
{fact();int n;while(~scanf("%d",&n)){if(n==0) {puts("0");continue;}int temp=0;for(int i=15;i>=1;i--) {if(a[i]<=n) {temp=i;break;}}while(temp!=0)//最小是到1的阶乘{int ans=n/a[temp];printf("%d",ans);n%=a[temp];temp--;}puts("");}return 0;
}不知道是什么原因,挺难理解这个题目的意思的
题目的意思是说,给定一个十进制数字,要求我们输出这个十进制数字的n!进制数字。这个定义比较奇怪,光看题干的21的例子,我还以为是把数位上的数字乘以该数字的阶乘,然后累加,累加的结果就是答案
但是事实上,10按照这个思路应该是1,100按照这个思路也是1,但是样例分别是120和4020
权重乘以系数就是总共的大小,观察一下数据范围,数据范围是3628799,这个数字是10的阶乘减去1,权重乘以系数,表示数字大小,每一位上的系数,从高位一直输出到最低位就是答案
要优先处理最高位,因为权重最大,假设优先处理最低位,很有可能会导致系数非常大,与实际情乱矛盾
所以思路就是,找到比当前十进制数字小的最大的阶乘,然后除以该阶乘,表示的是最高位的系数,输出这个系数,十进制数字n对该阶乘取余,表示的是剩下的数字的大小,然后把阶乘变成下一个阶乘(比如说4的阶乘变成3的阶乘,3的阶乘变成2的阶乘),一直到阶乘是1的阶乘,表示操作结束,输出换行即可
在循环里我们除了使用 if 这种条件判断,还可以使用 continue 表示后面的都不考虑,直接下一次循环,也非常方便
前面的 fact 函数是用来求阶乘的,fact是 factorial 英文的前四个字母,表示阶乘
另外发现写c语言题目还是用 c 语言比较友好,不然我辛苦写却不符合学弟学妹的需求,还是有点无奈的哈哈
笔者都大二了,还是不能随手秒掉这些 c语言题目,还是非常惭愧啊
E ICPC
#include<stdio.h>
#include<string.h>char s1[110],s2[110],s3[110];
int cnt[10];int main()
{int n;while(~scanf("%d",&n)){if(n==0) break;scanf("%s",s1+1);scanf("%s",s2+1);scanf("%s",s3+1);char ans;for(int i=1;i<=n;i++){ans=s1[i];if(s2[i]<ans) ans=s2[i];if(s3[i]<ans) ans=s3[i];printf("%c",ans);cnt[ans-'A'+1]++;}printf("\n");for(int i=1;i<=4;i++) printf("%d ",cnt[i]);printf("%d\n",cnt[5]);memset(cnt,0,sizeof cnt);}return 0;
}
算是简单的数组的使用
主要问题是空格……
还有就是不用c++的min函数确实写起来不是很熟练
输入字符的时候,空格也会读入,所以非常不方便,所以还是用字符串读入比较好,然后计数器数组每一次循环之后要重置,不然会影响下一次循环的结果
题目需要模拟的就是输入的数据里面,每一列的最小的字母,输出这个字母,然后给这个字母计数即可,注意输出的格式,防止PE
F coins
#include<stdio.h>int dp[45][2];int main()
{dp[1][0]=1;//正面dp[1][1]=1;//反面for(int i=2;i<=40;i++){dp[i][0]+=dp[i-1][1];dp[i][1]+=(dp[i-1][0]+dp[i-1][1]);}int n;while(~scanf("%d",&n)){if(n==0) break;printf("%d\n",dp[n][0]+dp[n][1]);}return 0;
}
做不出来,简单的动态规划题目……
不包含连续的正面的方案数目。意思就是,只能是全部是反面,正反交替,或者是反面+正反交替
本来以为正面不好枚举答案,然后发现反面也不好枚举答案
DP来做这题,首先是DP集合表示什么意思,第一维表示的是有多少个硬币,第二维表示的是正面或者反面两种情况,我们需要做的是枚举所有情况
状态计算的时候,0表示正面,正面前面可以放反面
1表示反面,反面前面任意放
代码很短,但是得有动态规划的思路,才能做出来
G 因子和
#include<stdio.h>int main()
{long long n;while(~scanf("%I64d",&n)){if(n==0) break;long long ans=0;for(int i=1;i*i<=n;i++){if(n%i==0){if(i==n/i) ans+=i;else ans+=i+n/i;}}printf("%I64d\n",ans);}return 0;
}
第一眼以为是前缀和,求1到n所有数字的和
直接按照题意模拟,用%lld输出,超时了,改成%I64d就过了
正解应该是要用算数基本定理的推论去分解质因数,然后套用公式求解
如果两个因子相等表示该数字是一个完全平方数,该因子只能被计算一次,如果不是的话就可以计算两次,分界点是输入的数字开根号
结语
总结就是,我感觉我C语言期末考试要爆零了,感觉一个题都做不来,慌……
相关文章:

湘潭大学-2023年下学期-c语言-作业0x0a-综合1
A 求最小公倍数 #include<stdio.h>int gcd(int a,int b) {return b>0?gcd(b,a%b):a; }int main() {int a,b;while(~scanf("%d%d",&a,&b)){if(a0&&b0) break;printf("%d\n",a*b/gcd(a,b));}return 0; }记住最大公约数的函数&…...
网络协议-BIO实战和NIO编程
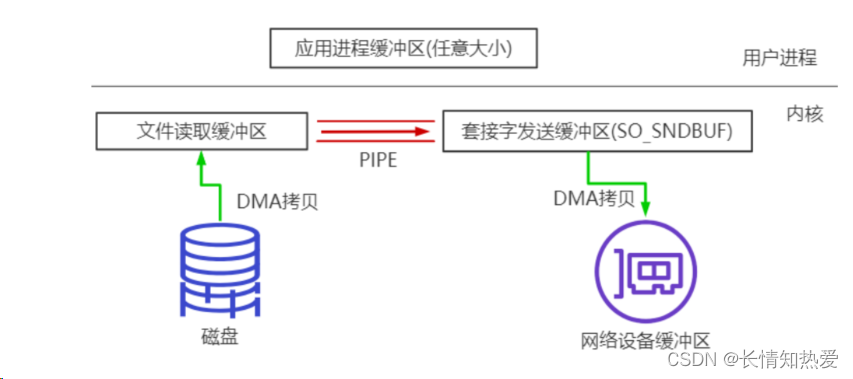
网络通信编程基本常识 在开发过程中,如果类的名字有 Server 或者 ServerSocket 的,表示这个类是给服务端容纳网络 服务用的,如果类的名字只包含 Socket 的,那么表示这是负责具体的网络读写的。 ServerSocket 并不负责具体的网络读…...
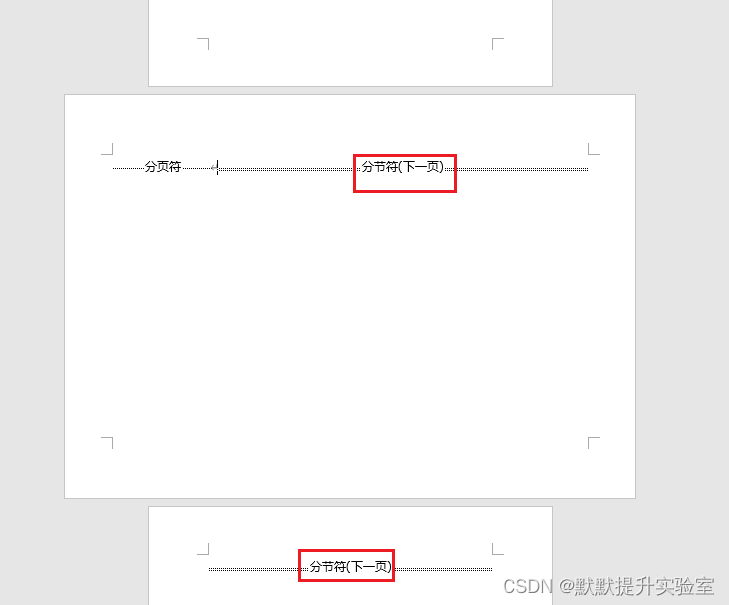
Word 将页面方向更改为横向或纵向
文章目录 更改整个文档的方向更改部分页面的方向方法1:方法2: 参考链接 更改整个文档的方向 选择“布局”>“方向”,选择“纵向”或“横向”。 更改部分页面的方向 需要达到下图结果: 方法1: 选:中你要在横向页面…...
关键字:abstract关键字
在 Java 中,abstract是一个关键字,用于修饰类和方法。当一个类被声明为抽象类时,它不能被实例化,只能被其他类继承。同时,抽象类可以包含抽象方法,抽象方法没有方法体,只包含方法的签名…...
从PDF中提取图片
由于工作需要,要从pdf文件中提取出图片保存到本地,项目中就引用到了Apache PDFBox库。 1 什么是Apache PDFBox? Apache PDFBox库,一个用于处理PDF文档的开源Java工具。它允许用户创建全新的PDF文件,操作现有的PDF文档࿰…...

推荐:一个不错的介绍Apache Doris的PPT
原来Apache Doris居然是百度开源出来的,不错。部分节选:完整下载地址网盘: 链接: https://pan.baidu.com/s/18WR70R_f72GxCjh0lykStQ 提取码: umd3 复制这段内容后打开百度网盘手机App,操作更方便哦 --来自百度网盘超级会员v7的分…...
】进度对话框QProgressDialog类的基本用法)
【Python_PySide2学习笔记(二十二)】进度对话框QProgressDialog类的基本用法
进度对话框QProgressDialog类的基本用法 进度对话框QProgressDialog类的基本用法前言一、QProgressDialog 的常用方法1、创建进度对话框2、进度对话框设置窗口标题3、进度对话框隐藏"最大化"、"最小化"、"关闭"4、进度对话框设置是否自动关闭5、…...

使用rust读取usb设备ACR122U的nfc卡片id
rust及其高效和安全著称,而且支持跨平台,所以就想使用这个rust开发一个桌面端程序,来读取nfc设备的nfc卡片的id信息,下面就做一个最简单的入门教程吧,也是我写的第三个rust应用。 当你电脑上安装好了rust环境之后&…...

servlet总结
目录 1.生命周期 2.线程总结 3.配置 4.请求和响应 5.会话管理 6.过滤和监听器 7.处理表单数据 8.与JSP集成 9.异常处理 10.安全性和认证 Servlet是一种基于Java的Web组件,用于处理客户端请求并生成动态Web内容。以下是关于Servlet的一些总结 1.生命周期 …...
Nacos2.1.2改造适配达梦数据库7.0
出于业务需求,现将Nacos改造适配达梦数据库7.0,记录本次改造过程。 文章目录 一、前期准备二、适配流程1、项目初始化2、引入驱动3、源码修改 三、启动测试四、打包测试 一、前期准备 Nacos源码,版本:2.1.2:源码下载…...
TPRI-DMP平台介绍
TPRI-DMP平台介绍 1 TPRI-DMP平台概述 TPRI-DMP为华能集团西安热工院自主产权的工业云PaaS平台,已经过13年的发展和迭代,其具备大规模能源电力行业生产应用软件开发和运行能力。提供TPRI-DMP平台主数据管理、业务系统开发与运行、应用资源管理…...
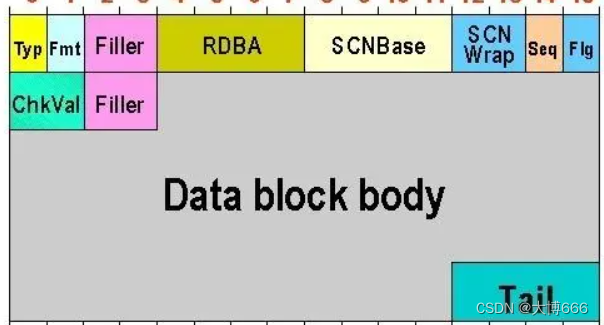
oracle-存储结构
文件包括 控制文件.ctl、数据文件.dbf、日志文件.log这三类放在存储上。 参数文件:空间的划分,进程的选用(.ora) oracle启动的时候需要读一下,数据库启动后,参数文件并不关闭,但即使文件丢了&a…...

获取PG库 database与 user 创建时间以及cluster初始化时间
代码实现 echo "获取数据库创建时间" data_dir$(psql -U postgres -d postgres -X -qAt -c "show data_directory" ) db_dirs$(ls $data_dir/base |grep -v pgsql_tmp) for db_oid in $db_dirs dodb_exists$(psql -U postgres -d postgres -X -qAt -c &qu…...

【12.29】转行小白历险记-刷算法05
242.有效的字母异位词 数组、set、map,数组是比较高效查找的 函数功能 判断字符串 s 和 t 是否互为字母异位词。如果它们包含相同的字符且每个字符出现的次数也相同,那么它们互为字母异位词。 代码逻辑 长度检查: if (s.length ! t.lengt…...
docker部署kafka zookeeper模式集群
单机模式链接:https://blog.csdn.net/wsdhla/article/details/133032238 kraft集群模式链接:部署Kafka_kafka 部署-CSDN博客 zookeeper选举机制举例: 目前有5台服务器,每台服务器均没有数据,它们的编号分别是1,2,3,4,5…...

Apache Flink连载(二十一):Flink On Yarn运行原理-Yarn Application模式
🏡 个人主页:IT贫道_大数据OLAP体系技术栈,Apache Doris,Clickhouse 技术-CSDN博客 🚩 私聊博主:加入大数据技术讨论群聊,获取更多大数据资料。 🔔 博主个人B栈地址:豹哥教你大数据的个人空间-豹哥教你大数据个人主页-哔哩哔哩视频 目录 1. 任务提交命令...

《深入理解C++11:C++11新特性解析与应用》笔记五
第五章 提高类型安全 5.1 强类型枚举 5.1.1 枚举:分门别类与数值的名字 具名枚举类型一般声明类似:enum Gender { Male, Female }。 匿名枚举类型可以使用三种方式实现: 第一种方式时宏,比如 #define Male 0 #define Femal…...
Y9000P + ubuntu22.04 配置Anaconda+pycharm +pytorch
Anaconda3 的安装及使用方法安装 Anaconda3 Anaconda3 是 Anaconda 的具体版本 Anaconda3 中的 Python 解释器默认使用的是 Python3.x 版本,而不是 Python2.x 版本 Python2.x 版本中,字符串是以 ASCII 编码处理的,而在 Python3.x 版本中&am…...

使用Ubuntu编译FFmpeg生成Android动态库/静态库
环境 我这里使用windows里的wsl2的ubuntu,使用物理机或者vmware,vbox之类的安装的ubuntu理论上也可以. gcc编译使用的环境如下: Ndk使用17 FFmpeg使用4.0.2. clang编译使用的环境如下: Ndk使用21.4 FFmpeg使用6.1 FFmpeg下载地址:https://ffmpeg.org/…...

【AIGC-图片生成视频系列-2】八仙过海,各显神通:AI生成视频相关汇总剖析
最近「图片生成视频系列」层出不穷,我拜读并结合实践(对,就是手撕代码,有开源就撕),并对以下几篇文章的相似点以及关键点稍微做个总结: 一. 生成视频中图像的一致性 在图像生成视频的这个过程…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...
