基于图搜索的自动驾驶规划算法 - BFS,Dijstra,A*
本文将讲解BFS,Dijstra,A*,动态规划的算法原理,不正之处望读者指正,希望有兴趣的读者能在评论区提出一些这些算法的面试考点,共同学习,一起进步
0 图论基础
图有三种:无向图、有向图、带权重的图
无向图

有向图

带权重的图

1 BFS
广度优先搜索算法
利用队列queue数据结构实现:先进先出
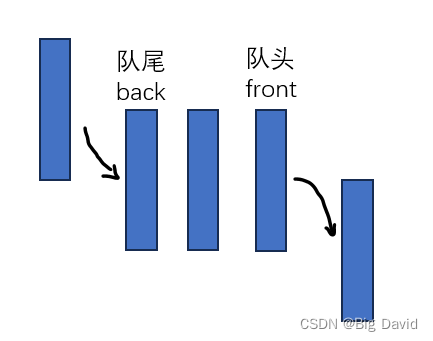
算法流程(伪代码):
BFS(G, start, goal):let Q be queue;Q.push(start);mark start as visited;while (!Q.empty()){v = Q.front();Q.pop();if (v is the goal) return v;for all neighbours n of v in GQ.push(n);n->parent = v;mark n as visited;}
BFS总结:
(1)相同探索所有的方向
(2)如果所有边权重为1,那么用BFS搜索出来的路径是cost最优的
(3)在不同的场景中,不能保证所有的边权重为1,对于这些场景,BFS受限
2 Dijstra
核心思想:
(1)相比BFS,Dijstra维护一个新变量g(n),g(n)表示从起始节点到当前节点的累积成本
(2)从openset(Min-priority queue)中访问累积成本g最低的节点
算法流程(伪代码):
Dijstra(G, start, goal):let open_list be priority_queue;open_list.push(start, 0);g[start] = 0;while (!open_list.empty()){current = open_list.pop();mark current as visited;if (current is the goal) return current;for (all unvisited neightbours next of current in G){next_cost = g[current] + cost(current, next);if (next is not in open_list)open_list.push(next, next_cost);else {if (g[next] > next_cost)g[next] = next_cost;}}}
优点:
(1)Dijstra算法能找到从起始节点到图上所有其他节点的最短路径
(2)Dijstra算法满足最优性
缺点:每次都会从open_list寻找代价最少的节点,但是并不知道终点在哪,如果用这个算法做图中特定两个点的最短路径,是比较低效的
3 A*算法
A*算法手撕版本见手撕A算法(详解A算法)
核心思想:
(1)相比Dijstra,A*将目标点的成本估计为启发式信息以提高效率
(2)启发式函数h(n):表示从节点n到目标的估计成本
(3)评估每个节点的成本函数:f(n)=g(n)+h(n)
(4)从open_list选择f-score最低的节点,而不是Dijstra算法中的g-score
算法流程(伪代码):
Astar(G, start, goal):let open_list be priority_queue;g[start] = 0;f[start] = g[start] + h[start];open_list.push(start, f[start]);while (!open_list.empty()){current = open_list.pop();mark current as visited;if (current is the goal) return current;for all unvisited neighbours next of current in Gnext_cost = g[current] + cost(current, next);if (next is not in open_list)open_list.push(next, next_cost + h[next]);else{if (g[next] > next_cost) {g[next] = next_cost;f[next] = next_cost + h[next];}}}
启发式函数设计
在路径搜索过程中,没有唯一启发函数设计原则,需要根据特定的任务来设计,如果最优性和距离相关,则可以计算节点之间的直线距离来估计
三种常用的距离:
起点: ( p 1 , p 2 ) (p_1, p_2) (p1,p2) 终点: ( q 1 , q 2 ) (q_1, q_2) (q1,q2)
(1)Euclidian distance
d ( p , q ) = ( q 1 − p 1 ) 2 + ( q 2 − p 2 ) 2 d(p,q)=\sqrt{(q_1-p_1)^2+(q_2-p_2)^2} d(p,q)=(q1−p1)2+(q2−p2)2
(2)Manhattan distance
d ( p , q ) = ∣ q 1 − p 1 ∣ + ∣ q 2 − p 2 ∣ d(p,q)=|q_1 - p_1|+|q_2 - p_2| d(p,q)=∣q1−p1∣+∣q2−p2∣
(3)Great circle distance

△ σ = a r c c o s ( s i n ϕ 1 s i n ϕ 2 + c o s ϕ 1 c o s ϕ 2 c o s ( △ λ ) ) \bigtriangleup \sigma =arccos(sin\phi _1sin\phi_2+cos\phi_1cos\phi_2cos(\bigtriangleup\lambda )) △σ=arccos(sinϕ1sinϕ2+cosϕ1cosϕ2cos(△λ))
d = r △ σ d = r\bigtriangleup \sigma d=r△σ
最优性
启发式函数 h ( n ) < c o s t ( n , g o a l ) h(n)<cost(n,goal) h(n)<cost(n,goal)
只要启发式函数提供了小于实际成本的估计,A*将始终找到最优路径,并且通常比Dijstra快
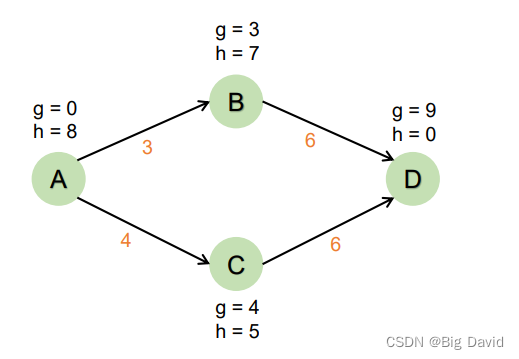
实际上A->B->D是最短路径
因为B的启发式函数高估了对目标的成本
这种高估导致搜索算法相信节点C总成本低于节点B,使得节点C在节点B之前访问,导致结果不是最优路径
在gridmap中如何设计启发式函数

使用8连接,曼哈顿距离启发式高估了成本
欧几里得距离总是可以接受
A*算法的精度和效率

(1) h ( n ) = 0 h(n)=0 h(n)=0:A退化为Dijstra
(2) h ( n ) < c o s t ( n , g o a l ) h(n)<cost(n,goal) h(n)<cost(n,goal):A满足最优性,效率比Dijstra更高
(3) h ( n ) = c o s t ( n , g o a l ) h(n)=cost(n,goal) h(n)=cost(n,goal):A满足最优性,并且有最高的效率
(4) h ( n ) > c o s t ( n , g o a l ) h(n)>cost(n,goal) h(n)>cost(n,goal):A不满足最优性,高估实际成本
BFS、Dijstra、A*总结:
| BFS | Dijstra | A* |
|---|---|---|
| (1)BFS算法会朝着周围等价扩展 | (1)相比BFS,Dijstra倾向于累积成本最小化,不是平等地搜索所有可能的路径,能在加权图中满足最优性 | (1)A*是Dijstra的修改,添加了启发式函数h(n)提高搜索效率 |
| (2)如果每条边权重为1,BFS搜索出来的path也是最优解 | (2)如果每条边权重为1,BFS=Dijstra | (3)启发式函数的设计会影响效率和准确性 |
搜索算法可视化参考:http://qiao.github.io/PathFinding.js/visual/
4 动态规划
- 定义:
一种计算机编程方式,首先把算法问题分解为子问题,求解这些子问题,并把这些结果保存下来,然后优化子问题找到整个问题的最优解
- 动态规划的性质:
(1)最优子结构
面对一个大问题可以分解为一系列子问题。如果能找到每个小问题的最优解,并且能够把小问题拼成大的问题。这种问题就叫最优子结构
(2)重复的子问题
动态规划不会重新计算重复的子问题,会事先保存结果
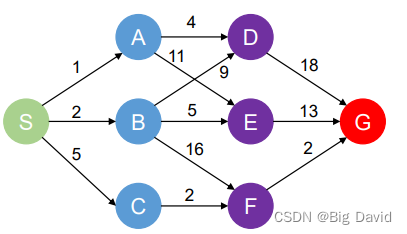
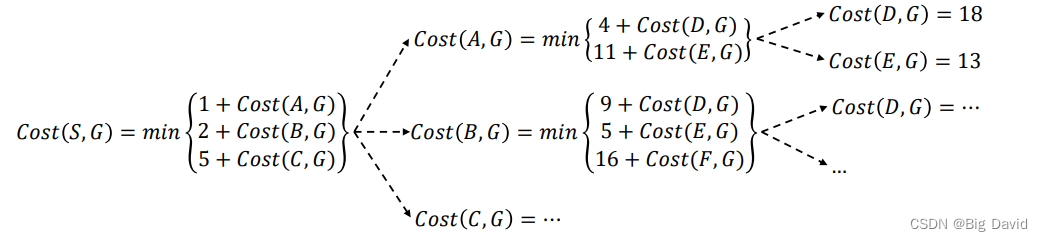
3. 计算方法
(1)前向法
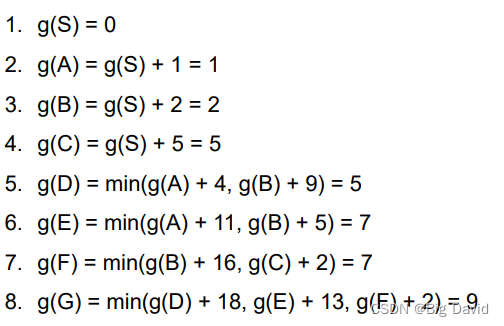
(2)逆向法
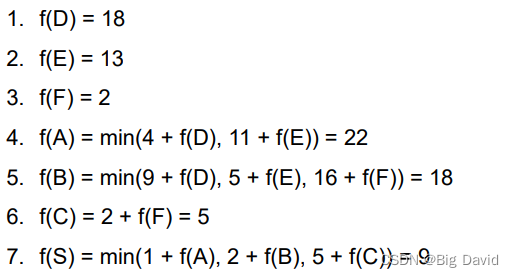
相关文章:
基于图搜索的自动驾驶规划算法 - BFS,Dijstra,A*
本文将讲解BFS,Dijstra,A*,动态规划的算法原理,不正之处望读者指正,希望有兴趣的读者能在评论区提出一些这些算法的面试考点,共同学习,一起进步 0 图论基础 图有三种:无向图、有向…...
Spring系列学习四、Spring数据访问
Spring数据访问 一、Spring中的JDBC模板介绍1、新建SpringBoot应用2、引入依赖:3、配置数据库连接,注入dbcTemplate对象,执行查询:4,测试验证: 二、整合MyBatis Plus1,在你的项目中添加MyBatis …...
)
HBase 创建不分裂的表 ( 禁止 Table Split )
注意:由于 HBase 版本众多,配置表的语法在不同版本上会有差异,本文介绍的配置方法是在 1.4.9 版本上测试的,使用 HBase 2.0 的版本需要核实并修改相关配置方法! 有时候,出于特殊需要,我们希望对…...

docker入门概念详解
本篇文章对docker的一些基础概念和周边概念进行了详细解释。帮助你可以很好的理解docker是用来干什么的,docker是怎么工作的。其中有docker所运用到的技术解释,docker的不同发展版本,dokcer的架构,docker的生态等等详解。希望本片…...

C++程序设计实践报告【格式】
C程序设计实践报告 原XX工业学院 C程序设计实践报告 题目: 专业: 学号: 姓名: 年 月 日 目录 一、绪…...

浅谈数据仓库运营
一、背景 企业每天都会产生大量的数据,随着时间增长,数据会呈现几何增长,尤其在系统基建基础好的公司。好的数据仓库需要提前规划和好的运营,才能支持企业的发展,为企业提供数据分析基础。 二、目标 提高数据仓库存储…...
系列六、Consul
一、Consul 1.1、概述 Consul是一套开源的分布式服务发现和配置管理系统,由HashiCorp公司用Go语言开发。他提供了微服务系统中的服务治理、配置中心、控制总线等功能。这些功能中的每一个功能都可以单独使用,也可以一起使用以构建全方位的服务网格&…...

Java集合/泛型篇----第一篇
系列文章目录 文章目录 系列文章目录前言一、ArrayList和linkedList的区别二、HashMap和HashTable的区别三、Collection包结构,与Collections的区别四、泛型常用特点前言 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站…...

集合使用注意事项
集合使用注意事项总结 集合判空 判断所有集合内部的元素是否为空,使用 isEmpty() 方法,而不是 size()0 的方式 这是因为 isEmpty() 方法的可读性更好,并且时间复杂度为 O(1)。 集合转 Map 在使用 java.util.stream.Collectors 类的 toMap()…...

什么是 JavaScript 中的 WeakMap
在 JavaScript 中,WeakMap 是一种特殊的 Map 数据结构,它允许将对象作为键,而且键值对是弱引用的关系。 与 Map 不同的是,WeakMap 的键只能是对象,不能是其他类型的值。同时,当键对象没有任何引用时&#…...
nodejs+vue+ElementUi农产品团购销售系统zto2c
目标是为了完成小区团购平台的设计和实现,在疫情当下的环境,方便小区业主购入生活所需,减小居民的生活压力 采用B/S模式架构系统,开发简单,只需要连接网络即可登录本系统,不需要安装任何客户端。开发工具采…...
nacos入门篇001-安装与启动
1、下载zip包 我这里下载的是版本2.2.0 Nacos 快速开始 2、修改配置文件 2.1集群模式修改成单例模式 vi startup.sh 2.2 修改数据库配置信息 3、初始化数据库 3.1 创建db名称:db_nacos 3.2 执行mysql-schema.sql 3.3 执行完截图: 4、运行脚本启动 …...
WordPress主题大前端DUX v8.3源码下载
DUX主题8.3版本更新内容: 新增:Cloudflare Turnstile 免费验证功能 新增:子菜单页面模版,支持多级页面 新增:手机端文章内表格自动出现横向滚动条,可集体或单独设置滚动宽度 新增:标签云页面模版…...
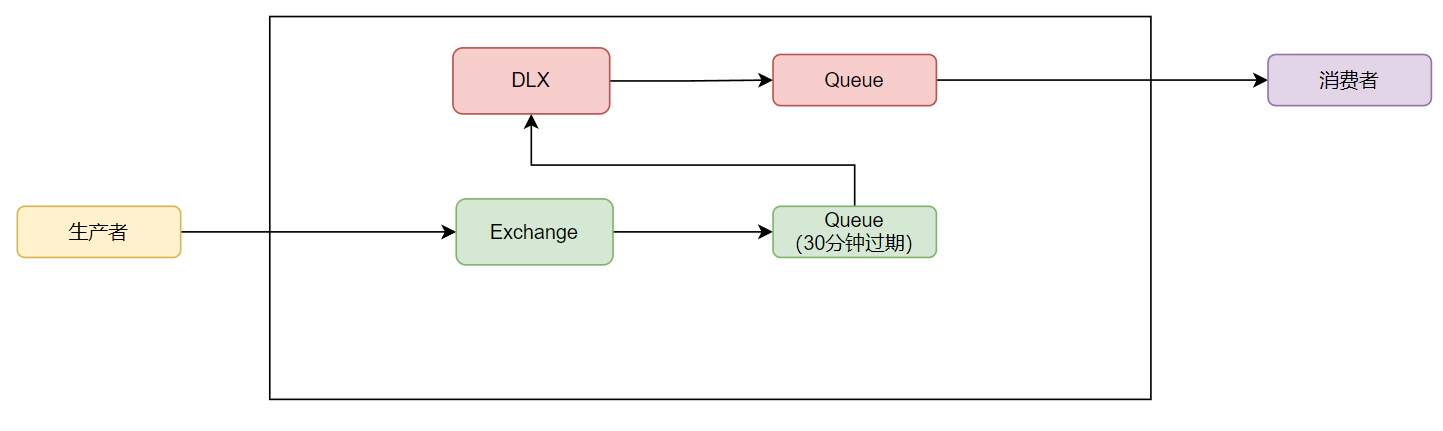
RabbitMQ之快速入门、上手
前言 学习一样新技术、新框架,最重要的是学习其思想、原理。即原理性思维。 如果是因为工作原因,需要快速上手RabbitMQ,本篇或许适合你。 核心概念 Connection:publisher/consumer 和 broker 之间的 TCP 连接Channel…...
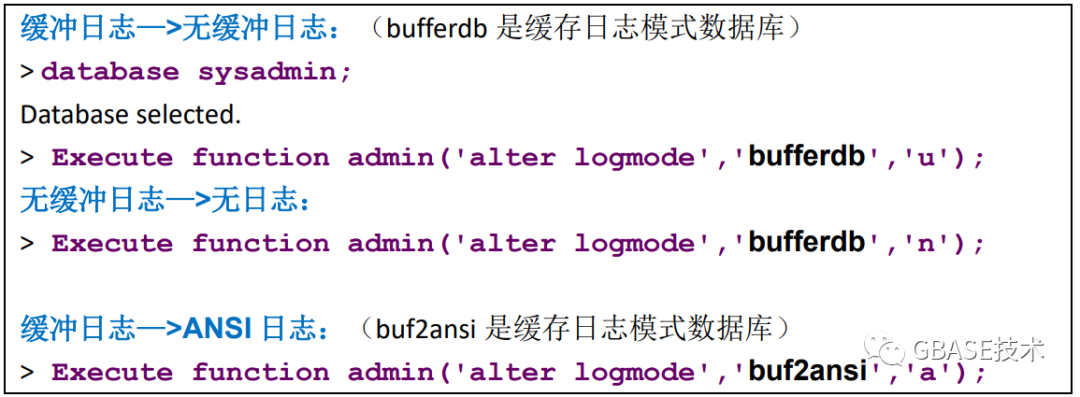
GBASE南大通用-GBase 8s数据库日志模式及切换
一、 GBase 8s数据库共有以下 4 种日志模式:无日志模式、缓冲日志模式、无缓冲日志模式、ANSI 模式。详细介绍如下: 1、无日志模式(Non logging): 采用无日志模式时,所有 DML 操作都不会被记录到日志中&…...

侵入式和非侵入式微服务框架的比较
微服务框架可以分为侵入式和非侵入式两种。侵入式框架需要对现有代码进行改造,而非侵入式框架则无需改造现有代码。 侵入式框架 侵入式框架将微服务治理功能嵌入到应用程序中,需要修改应用程序的代码。这种框架的优点是可以提供更强大的功能࿰…...

Go语言程序设计-第5章--函数
Go语言程序设计-第5章–函数 5.1 函数声明 每个函数声明都包含一个名字、一个形参列表、一个可选的返回列表以及函数体: func name(parameter-list) (result-list) {body }func add(x int, y int) int { return x y} func sub(x, y int) (z int) {z x - y; return} func f…...

数据被锁?被.mkp 勒索病毒攻击后的拯救行动
导言: 网络安全面临着越来越多的挑战,而.mallox勒索病毒则成为数字威胁中的一股强大势力。它的威胁不仅体现在其高度复杂的加密算法上,还表现在对受感染系统的深度渗透和数据的极大破坏上。以下是.mallox勒索病毒的主要威胁:如不…...

Fine-Tuning Language Models from Human Preferences
Abstract 奖励学习(reward learning)可以将强化学习(RL)应用到由人类判断定义奖励的任务中,通过询问人类问题来构建奖励模型。奖励学习的大部分工作使用了模拟环境,但是关于价值的复杂信息经常是以自然语言的形式表达的。我们相信语言奖励学习是使强化学习在现实世界任务…...
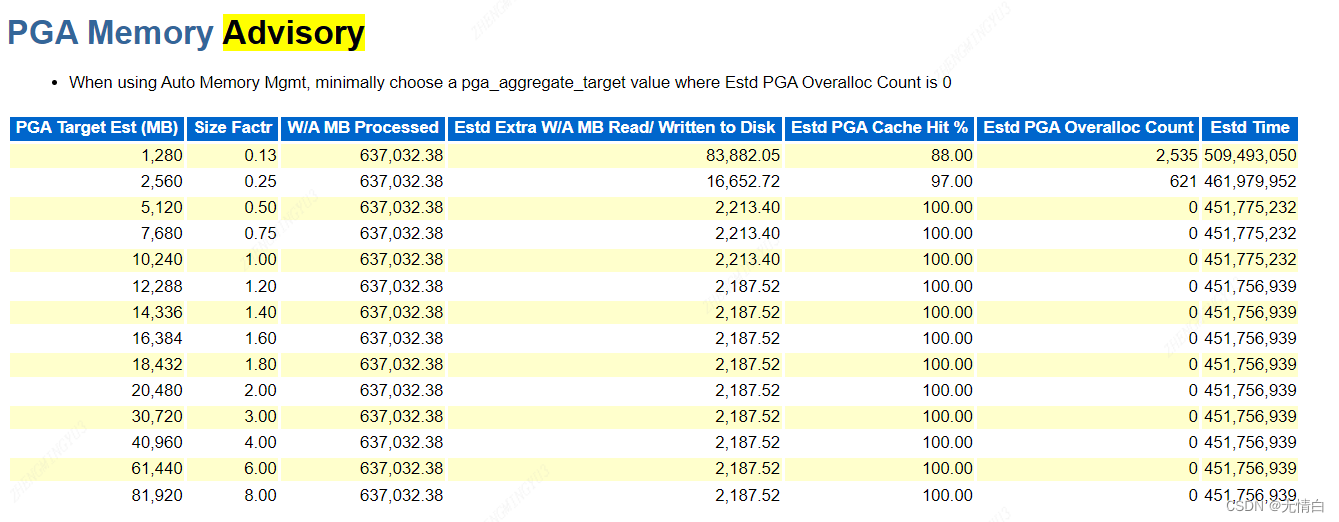
提升数据库性能的关键指南-Oracle AWR报告
文章目录 一、了解AWR报告:数据库性能的仪表盘二、生成AWR报告三、解读AWR报告的关键部分1.报告开头的系统基础信息2.ADDM发现3.负载概览(Load Profile)4.参数文件5.顶级前台等待事件6.SQL 统计信息-顶级SQL7.SGA Advisory AND PAG Advisory 一、了解AWR报告&#x…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...
