【动态规划精选题目】3、简单多状态模型

此动态规划系列主要讲解大约10个系列【后续持续更新】
本篇讲解简单多状态模型中的9道经典题,会在讲解题目同时给出AC代码
目录
1、按摩师
2、力扣198:打家劫舍1
3、打家劫舍II
4、删除并获得点数
5、 粉刷房子
6、力扣309:买卖股票的最佳时机含冷冻期
7、 买卖股票的最佳时机含手续费
8、买卖股票的最佳时机III
9、买卖股票的最佳时机IV
1、按摩师
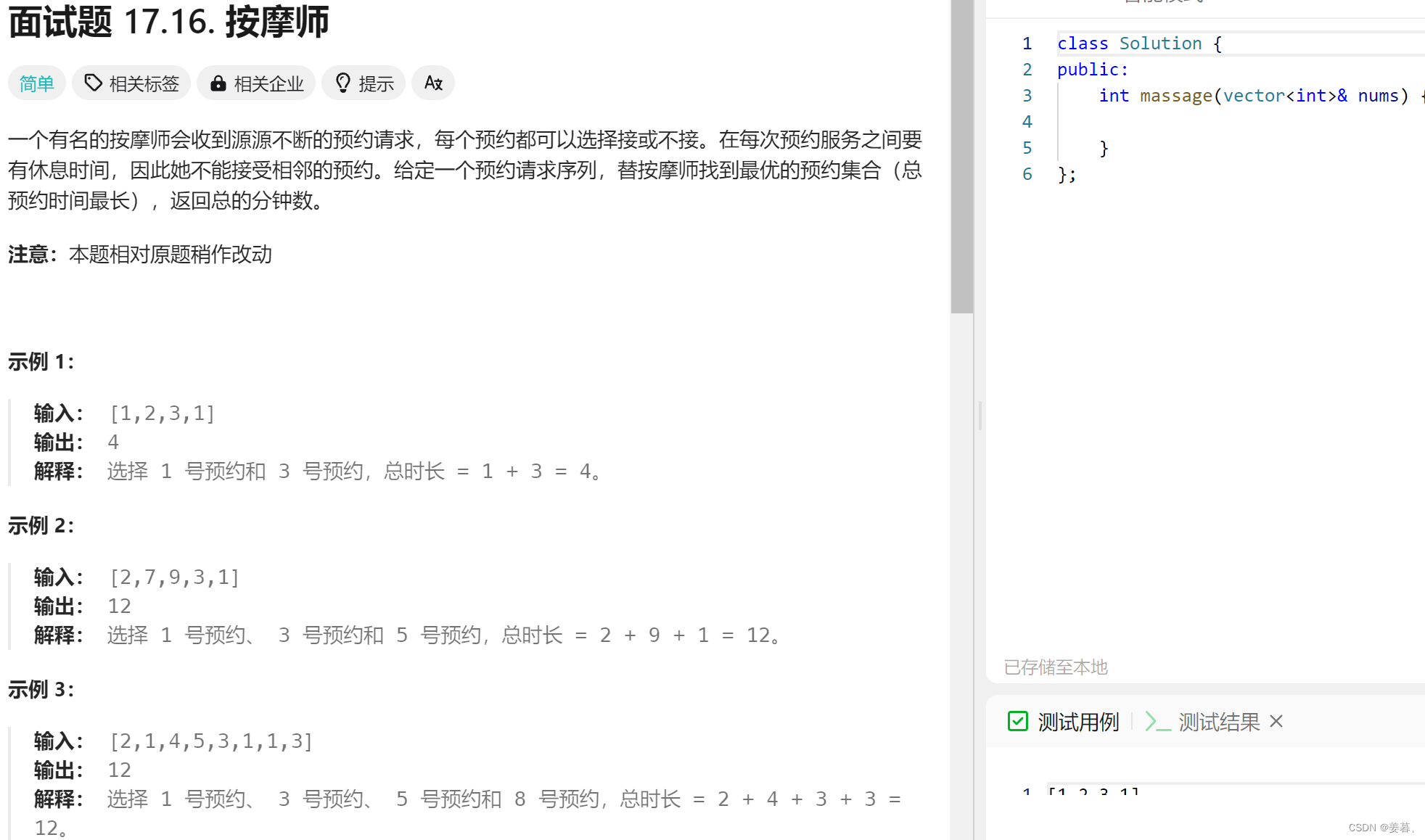
示例分析:




class Solution {
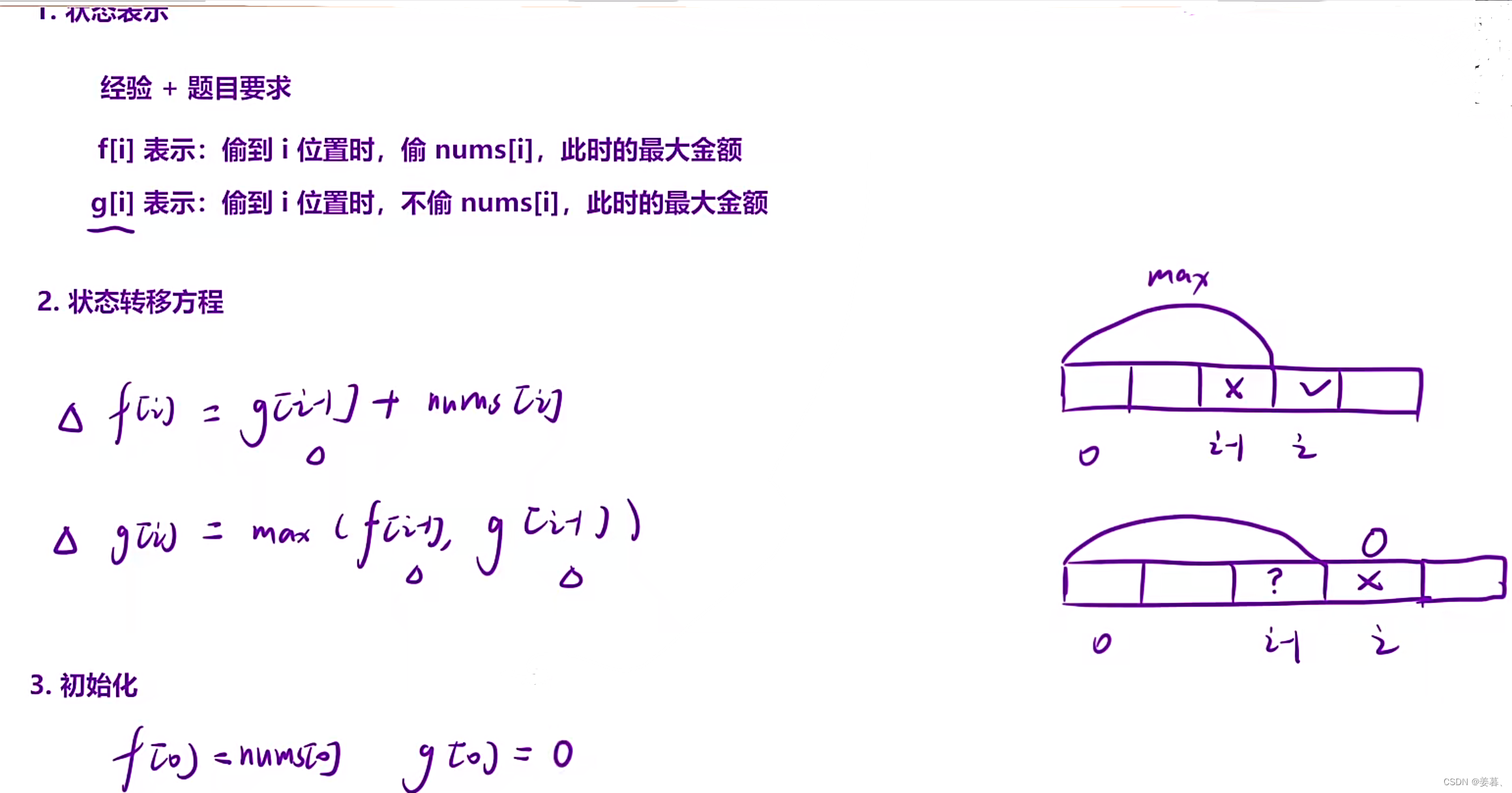
public:int massage(vector<int>& nums) {int n = nums.size();if (n == 0) return 0;//创建两个dp表f和gvector<int> f(n);//n个数据都会初始化为0auto g = f;//创建g表f[0] = nums[0]; //初始化for (int i = 1; i < n; i++){f[i] = g[i - 1] + nums[i];g[i] = max(f[i - 1], g[i - 1]);}return max(f[n - 1], g[n - 1]); }
};借多状态dp的题说明一下,怎么判断是一维dp还是二维dp呢?
是由状态表示决定的,如果一维数组能表示清楚,就用一维的,表示不清楚,就可以尝试增加维数,用二维的,有时候其实三维的也有,但是情况少。
2、力扣198:打家劫舍1
 这道题跟上道题的按摩师的思路和代码基本一样
这道题跟上道题的按摩师的思路和代码基本一样

class Solution {
public:int rob(vector<int>& nums) {int n = nums.size();vector<int> f(n);auto g = f;f[0] = nums[0];for (int i = 1; i < n; i++){f[i] = g[i - 1] + nums[i];g[i] = max(g[i - 1], f[i - 1]);}return max(f[n - 1], g[n - 1]);}
};3、打家劫舍II
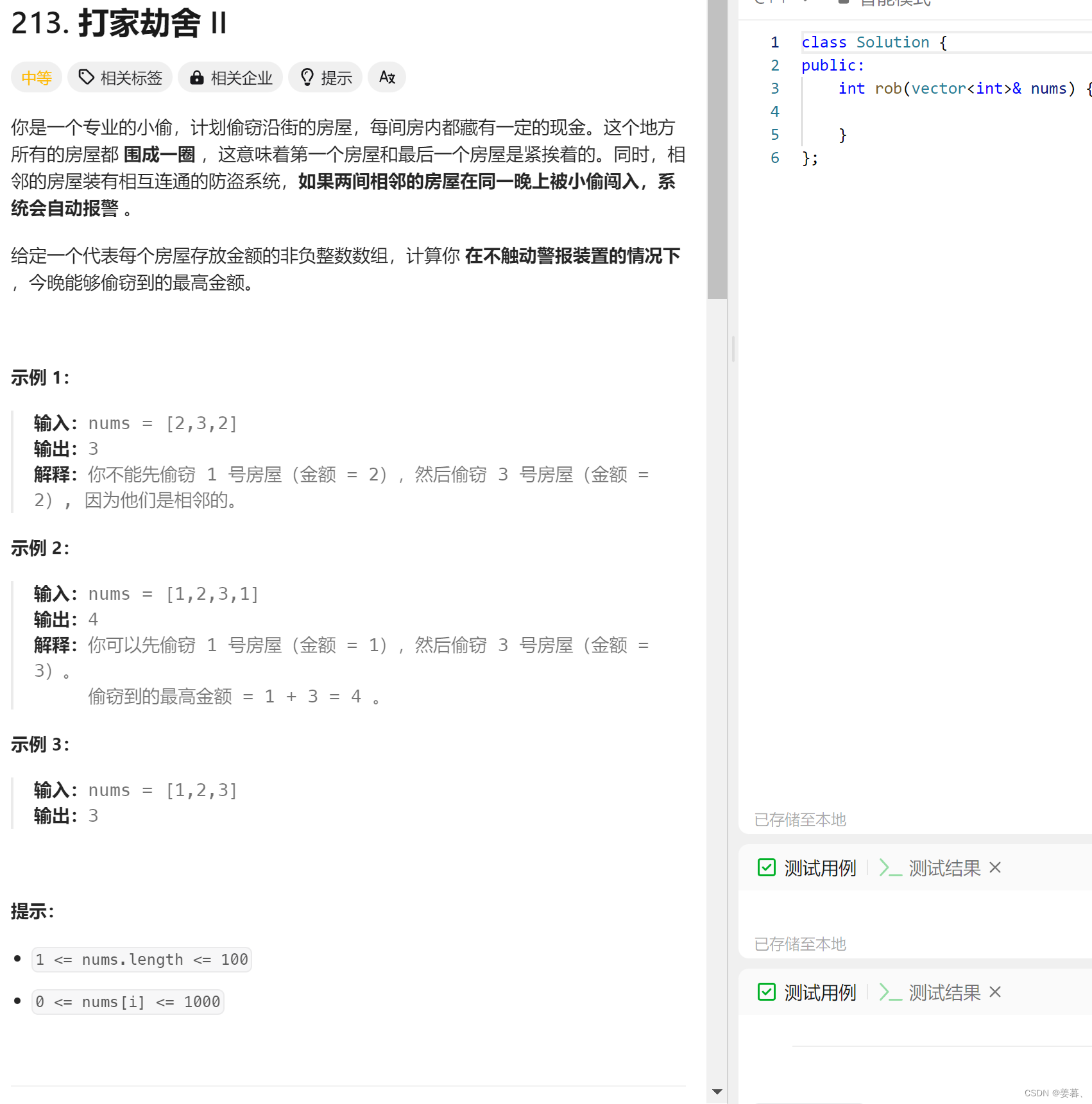
这道题只是在上一道题的打家劫舍1中加了一个限制条件,即首尾也算相连,不能都偷窃,所以只需分类讨论下这个情况,再转换为打家劫舍1即可(下面的rob1表示的是可以偷的范围,也就是可以用打家劫舍1来求解的地方)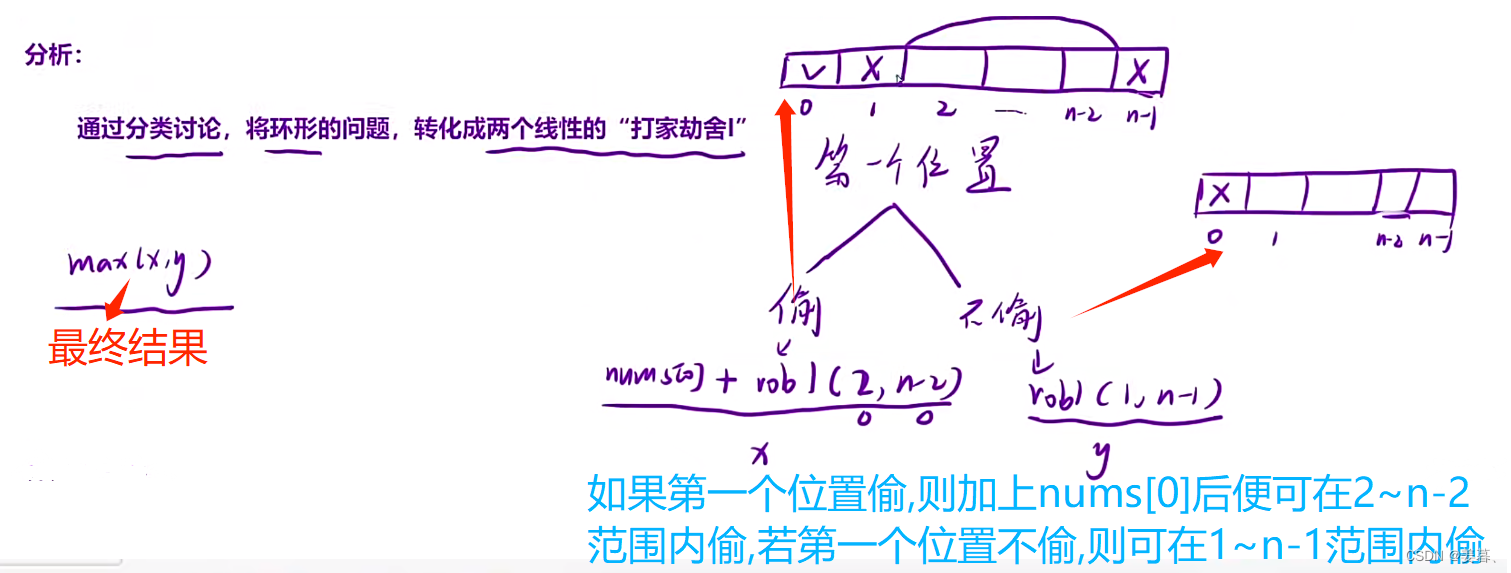
class Solution {
public:int rob(vector<int>& nums) {int n = nums.size();return max(nums[0] + rob1(nums, 2, n - 2), rob1(nums, 1, n - 1));}int rob1(vector<int>& nums, int left, int right){if (left > right) return 0;//处理边界条件int n = nums.size();//按理说开right-left+1个空间即可,但这里多开几个也没事vector<int> f(n);auto g = f;f[left] = nums[left];//初始化for (int i = left + 1; i <= right; i++){f[i] = g[i - 1] + nums[i];g[i] = max(f[i - 1], g[i - 1]);}return max(f[right], g[right]);}
};4、删除并获得点数

 动态规划的预处理思路:
动态规划的预处理思路:
其实上面的思想就是利用哈希表中的直接映射法,那么这种方法就要找nums数组中的最大值,但是题目中已经给出了nums数组中每个值的范围,故可以直接开空间大小为最大值。并且这种方法既做到了数据有序又做到了连续
整体思路:


class Solution {
public:int deleteAndEarn(vector<int>& nums) {const int N = 10001;//数组中的最大值为1万,多开1个防止越界问题//1、预处理int arr[N] = {0};for (const auto& x : nums) arr[x] += x;//2、利用打家劫舍思路求解该问题vector<int> f(N);auto g = f;//这里不用初始化了,因为f[0]=arr[0],可arr[0]本来就=0for (int i = 1; i < N; i++){f[i] = g[i - 1] + arr[i];g[i] = max(f[i - 1], g[i - 1]);}return max(f[N - 1], g[N - 1]);}
};5、 粉刷房子
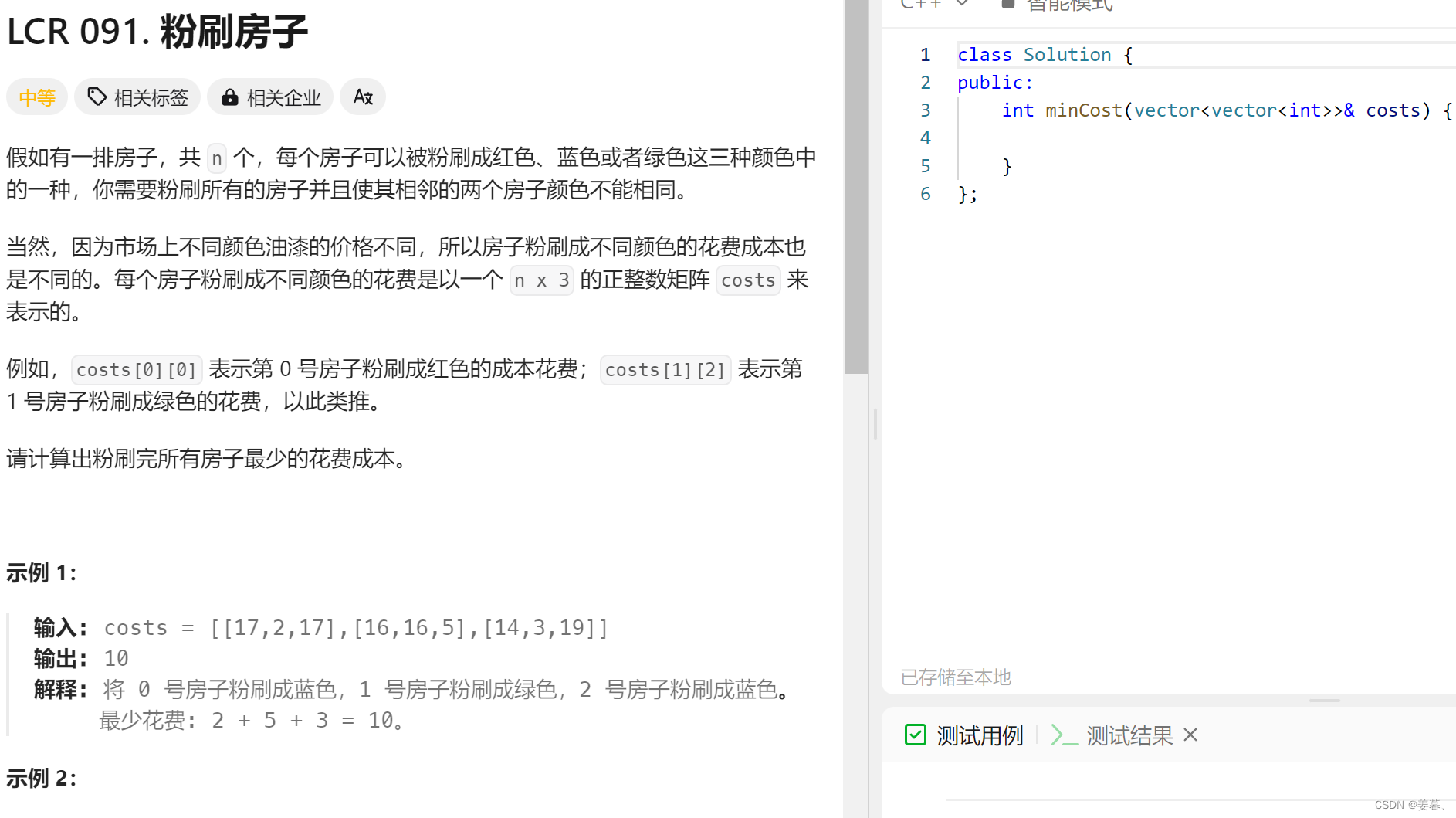

解释示例1和示例2:

也就是判断当前位置是第几个房子,只需看行即可,列是代表颜色的
总体思路:
下面说的位置可以理解为是一个房子
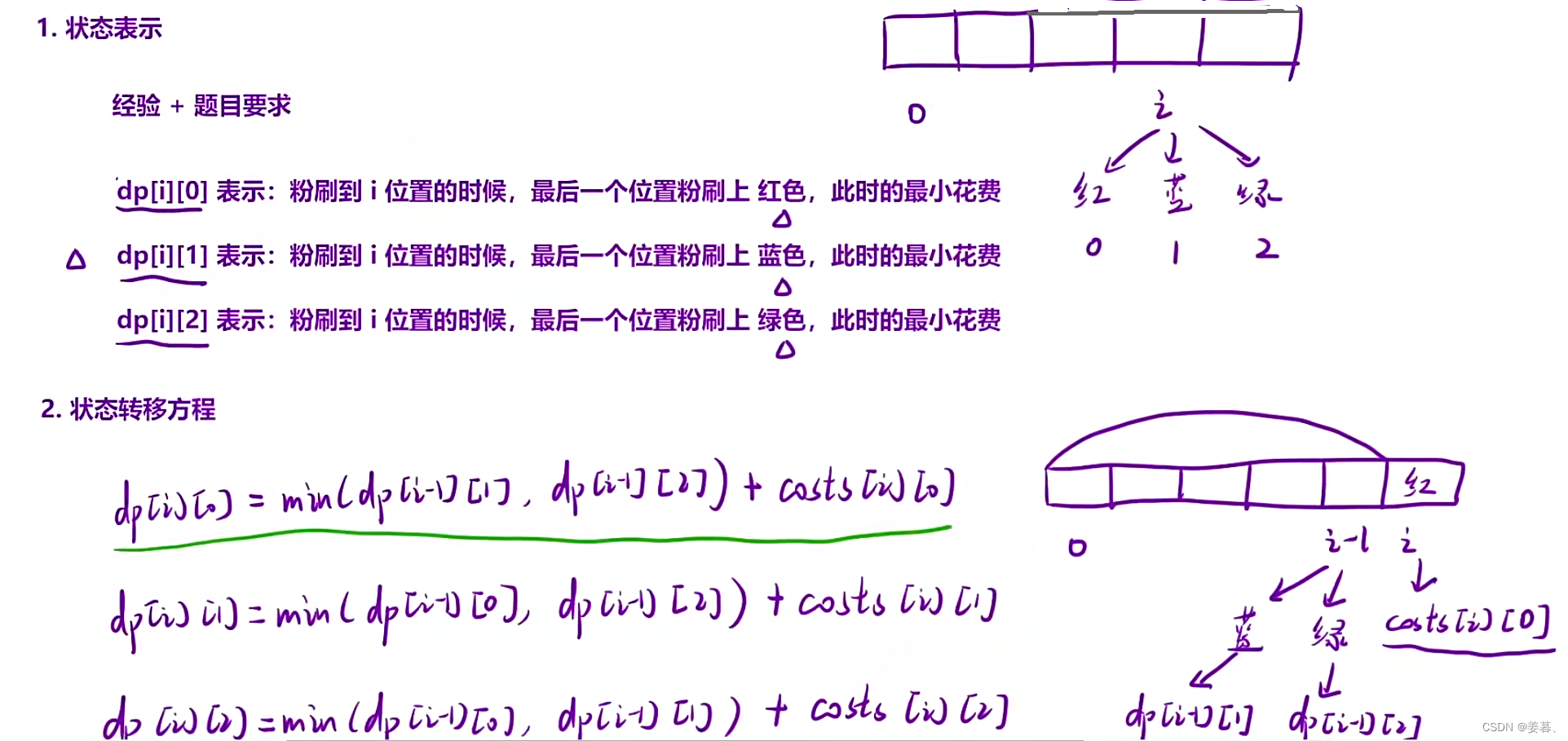
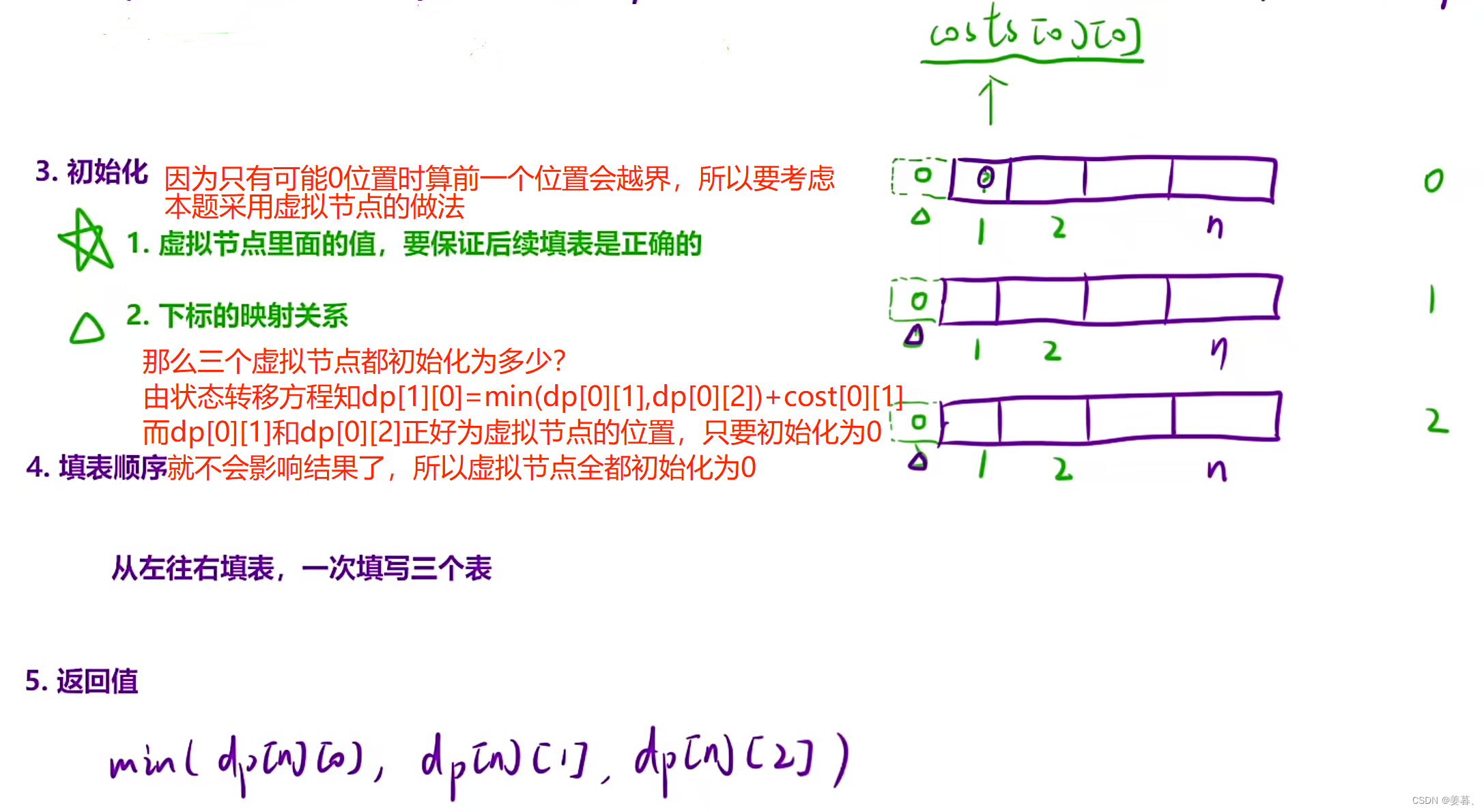
理解本题的虚拟节点:
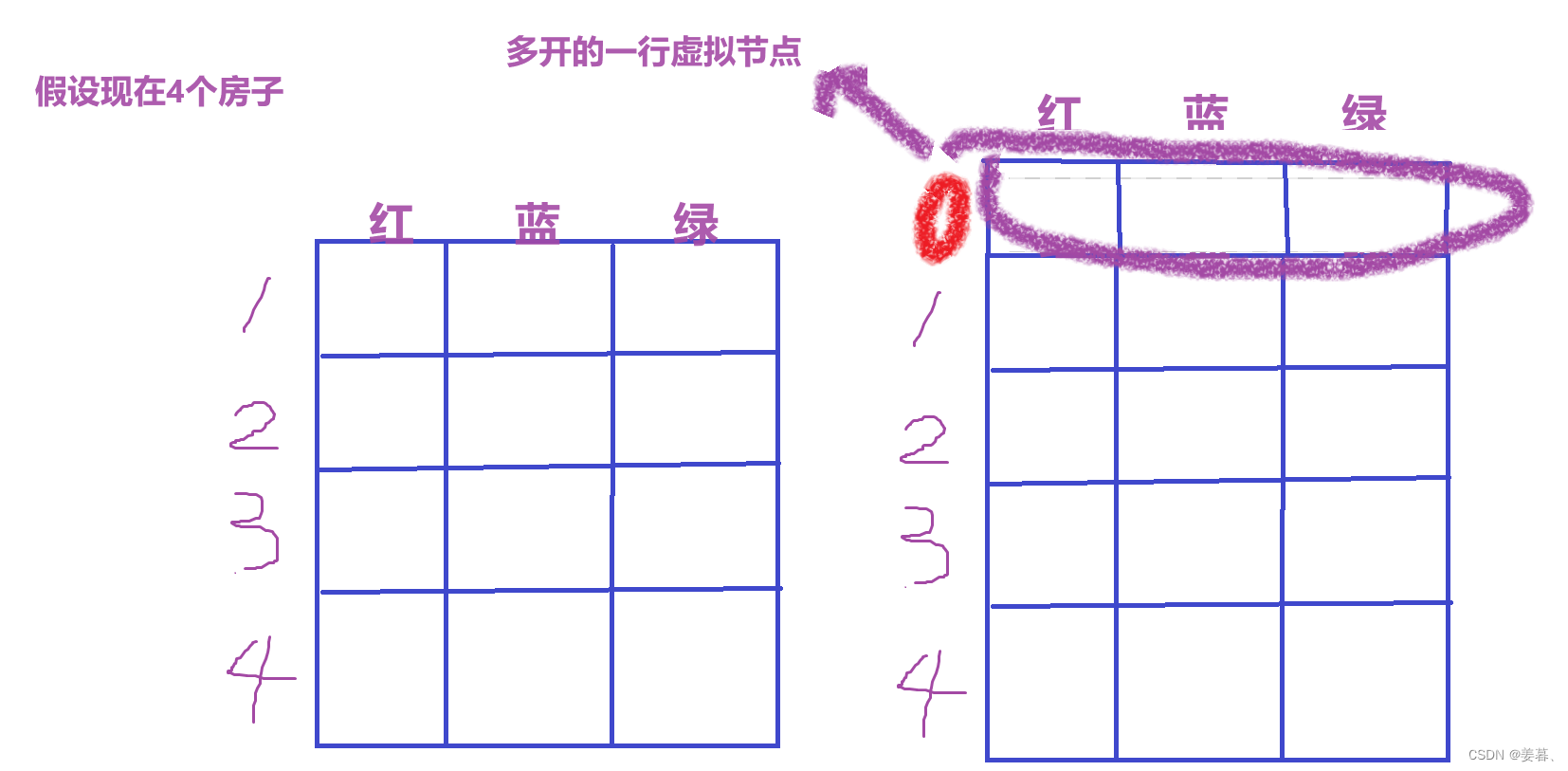
class Solution {
public:int minCost(vector<vector<int>>& costs) {int n = costs.size();//得到的是行数,即现有的房子数vector<vector<int>> dp(n + 1, vector<int> (3));//多开一行给虚拟节点//从上到下遍历每个房子,算出每个房子对应不同颜色的价格for (int i = 1; i <= n; i++){//因为多开了一个虚拟节点,所以要加上cost[i-1][0],这里要用i-1才行dp[i][0] = min(dp[i - 1][1], dp[i - 1][2]) + costs[i- 1][0];dp[i][1] = min(dp[i - 1][0], dp[i - 1][2]) + costs[i- 1][1];dp[i][2] = min(dp[i - 1][1], dp[i - 1][0]) + costs[i- 1][2];}return min(min(dp[n][0], dp[n][1]), dp[n][2]);}
};6、力扣309:买卖股票的最佳时机含冷冻期
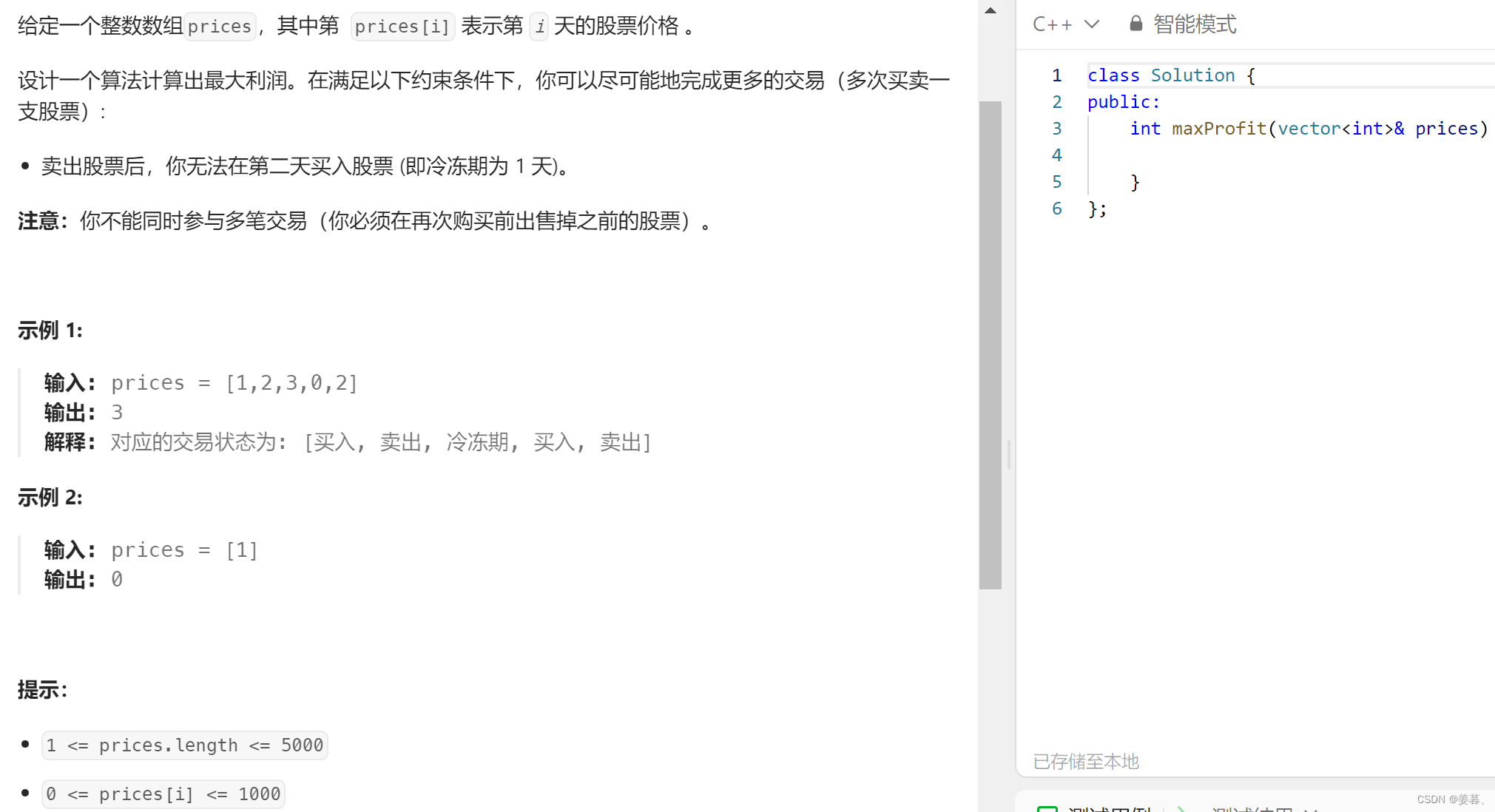
题目分析:


如果是多状态,并且多状态之间可以相互转移的话 ,为了不忽略某种状态,我们可以画一个图,如下图,我们也称为这种图为状态机
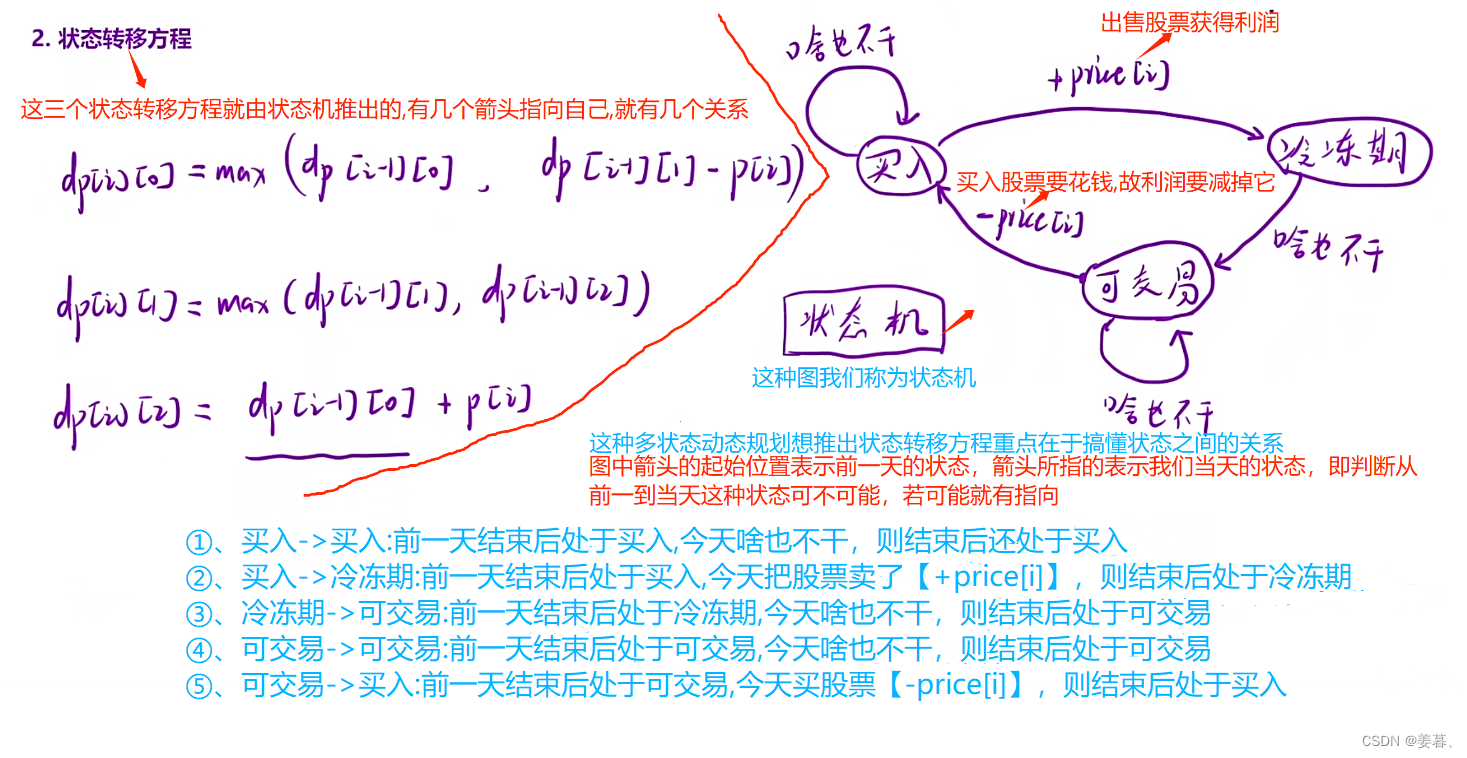

class Solution {
public:int maxProfit(vector<int>& prices) {int n = prices.size();vector<vector<int>> dp(n, vector<int>(3));//三个dp表dp[0][0] = -prices[0];//初始化 for (int i = 1; i < n; ++i){dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);dp[i][1] = max(dp[i - 1][1], dp[i - 1][2]);dp[i][2] = dp[i - 1][0] + prices[i];}//最佳答案一定不会是dp[n - 1][0],所以最后不用考虑在内return max(dp[n - 1][1], dp[n - 1][2]);}
};7、 买卖股票的最佳时机含手续费
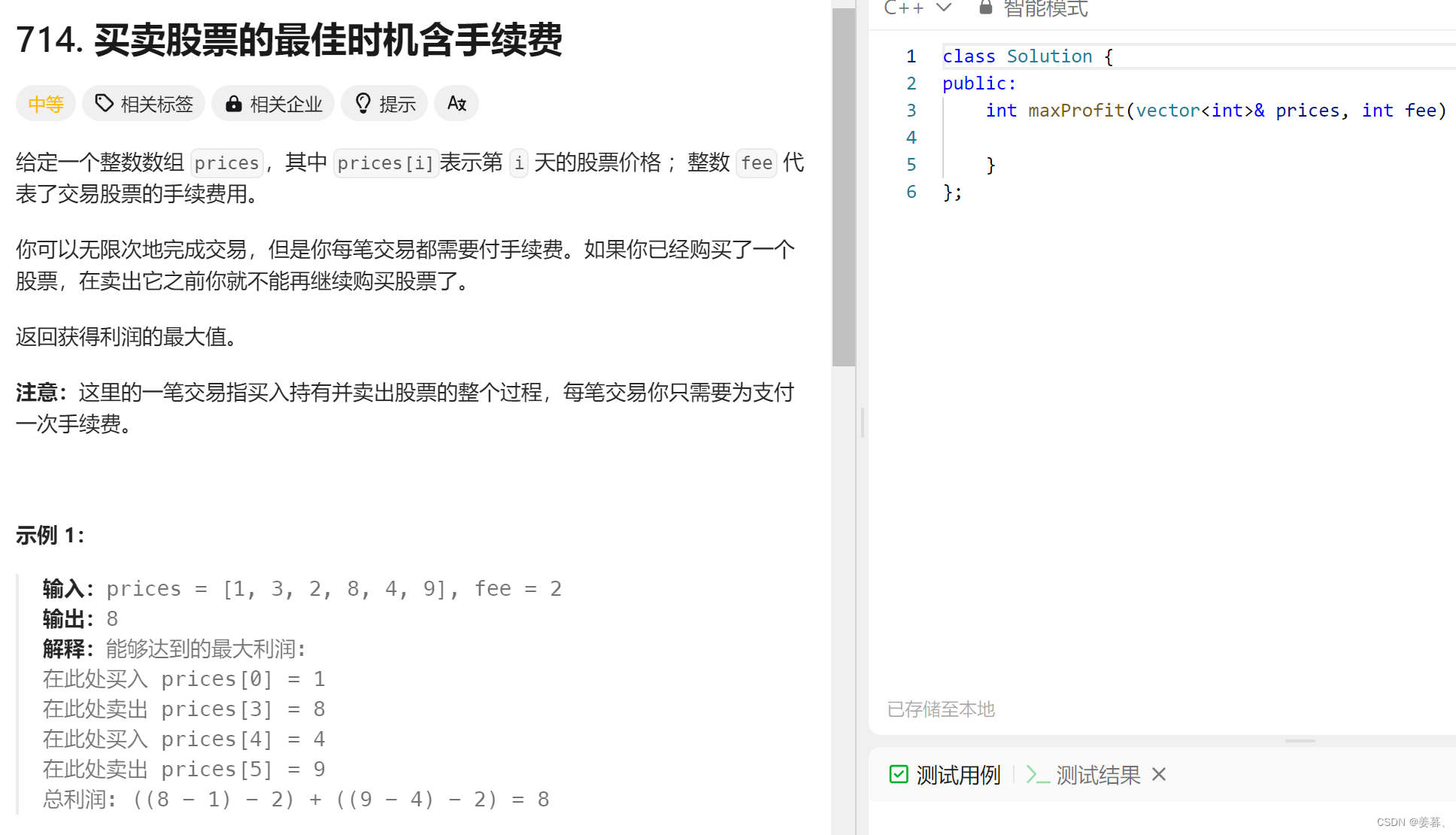
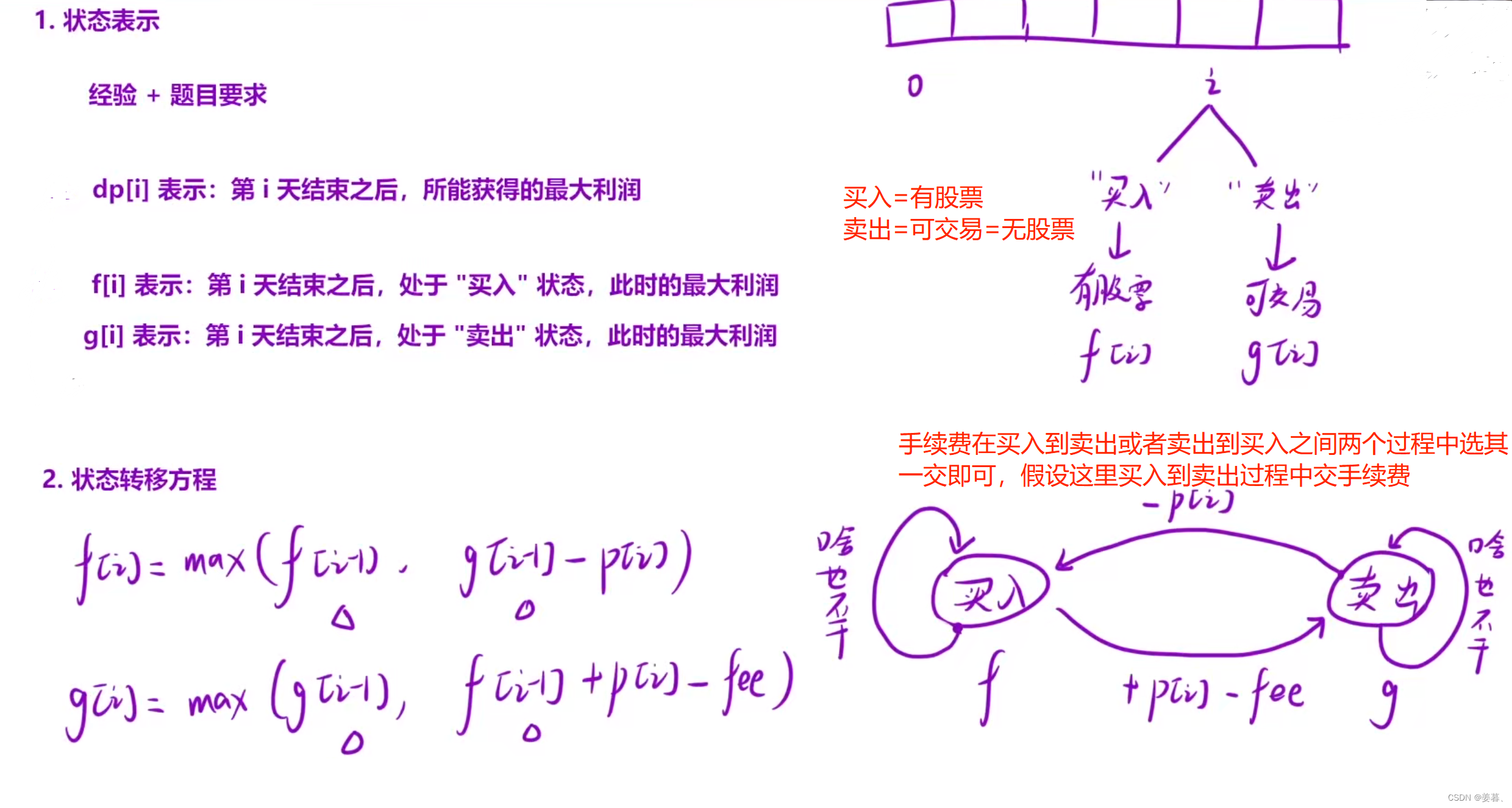
 示例解释:
示例解释:

箭头起始位置:前一天结束后的状态,箭头指向位置:当天结束状态

class Solution {
public:int maxProfit(vector<int>& prices, int fee) {int n = prices.size();vector<int> f(n);auto g = f;f[0] = -prices[0];//初始化:第0天结束后处于买入状态for (int i = 1; i < n; i++){f[i] = max(f[i- 1], g[i - 1] - prices[i]);g[i] = max(f[i - 1] + prices[i] - fee, g[i - 1]);}//最后一天手里还有股票,肯定就不是最优解,故不用考虑return g[n - 1];}
};当然,像之间那种开二维数组也可以,但是三种状态及以上才推荐开二维数组,下面这么写也可以

8、买卖股票的最佳时机III

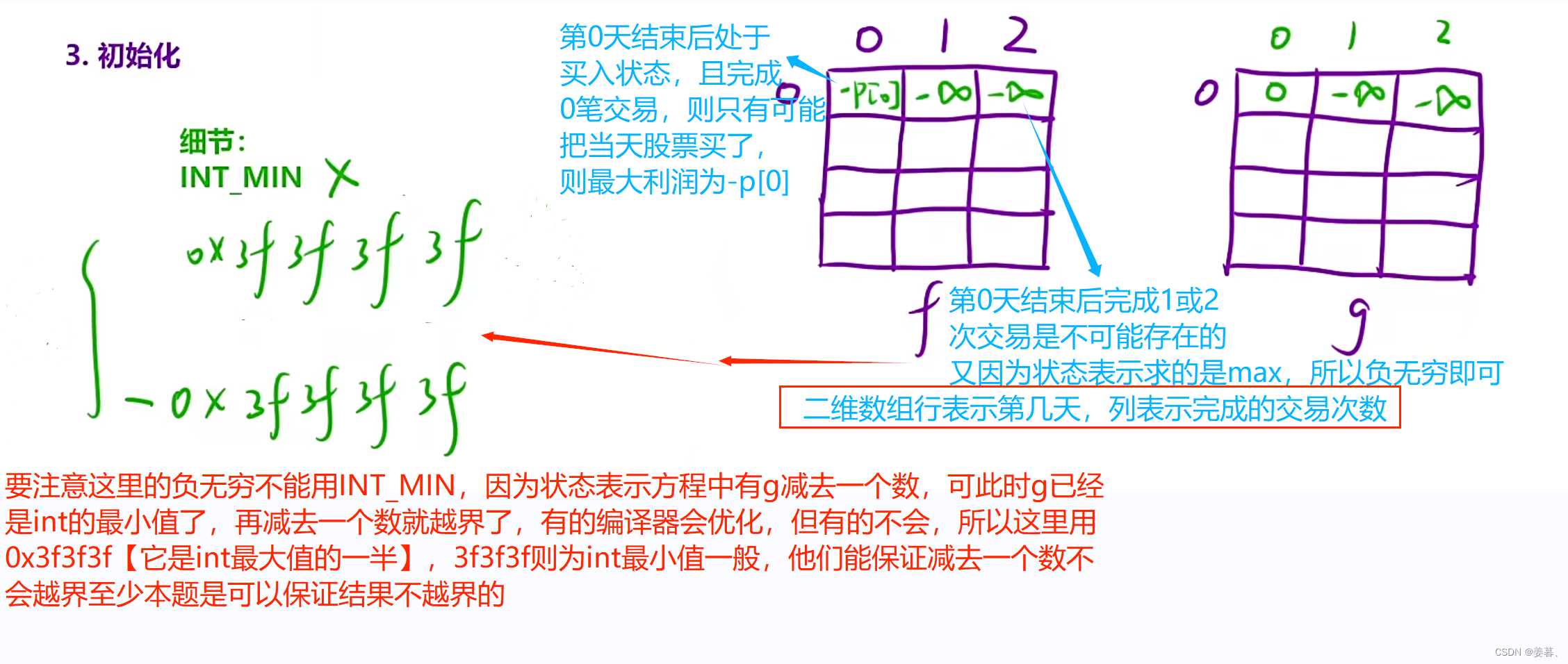
示例分析:
此题复杂在还要考虑交易的次数。

买入是指手里有股票的状态,卖出是指手里没股票,是一个可交易的状态。下图的线的含义,线的起点表示前一天结束后的状态,线表示当天的操作,箭头所指的表示当天结束后的状态

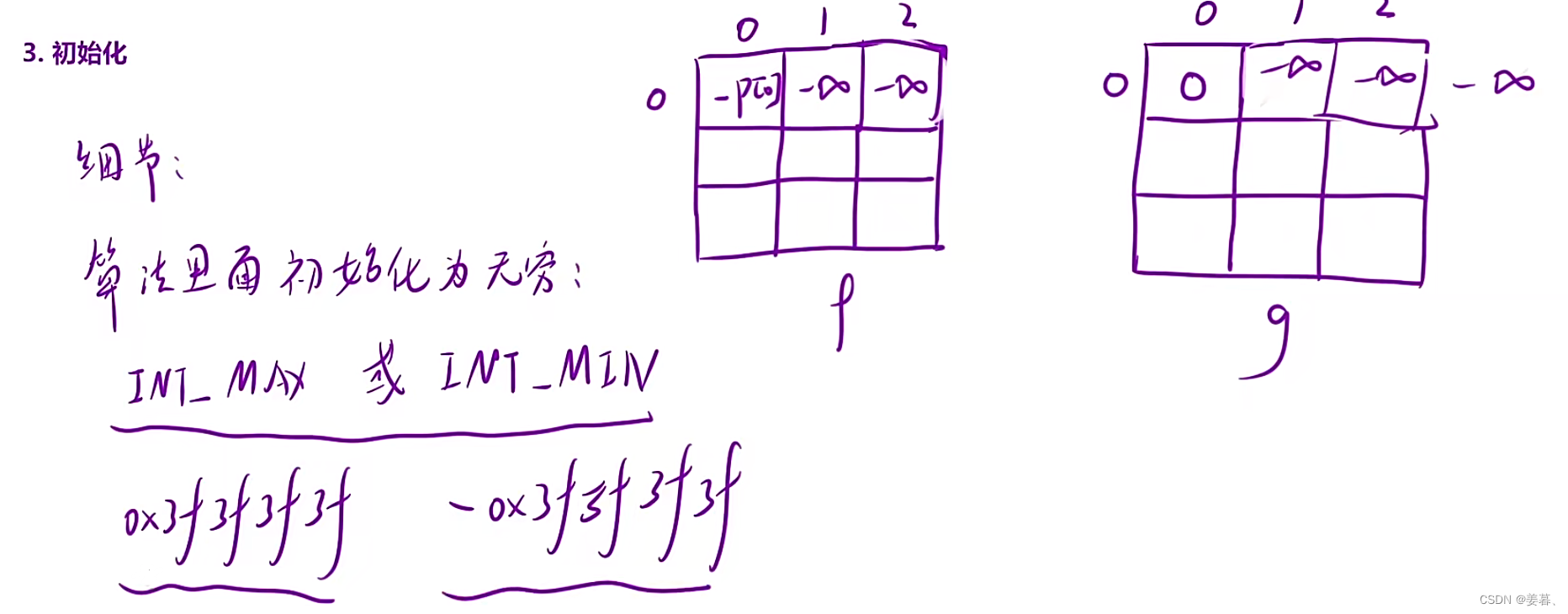
但是因为f和g表初始化的不一致,可又不想在循环外再初始化哪个特例,就用稍微修改状态转移方程的方法来便于统一的初始化

class Solution {
public:const int INF = 0x3f3f3f;//int最大值的一半int maxProfit(vector<int>& prices) {int n = prices.size();vector<vector<int>> f(n, vector<int>(3, -INF));auto g = f;//初始化f和g表的第一行的第一个元素f[0][0] = -prices[0], g[0][0] = 0;for (int i = 1; i < n; i++){for (int j = 0; j < 3; j++){f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i]);//天数不会越界,因为在这之前f和g表已经初始化了g[i][j] = g[i - 1][j];if (j - 1 >= 0){ //要么j-1交易次数存在,则考虑这种情况,//要么不存在,那么g[i][j]就直接=g[i-1][j]g[i][j] = max(g[i][j], f[i -1][j - 1] + prices[i]);}}}//找到g表最后一行的最大值int ret = 0;for (int i = 0; i < 3; i++)ret = max(g[n - 1][i], ret);return ret; }
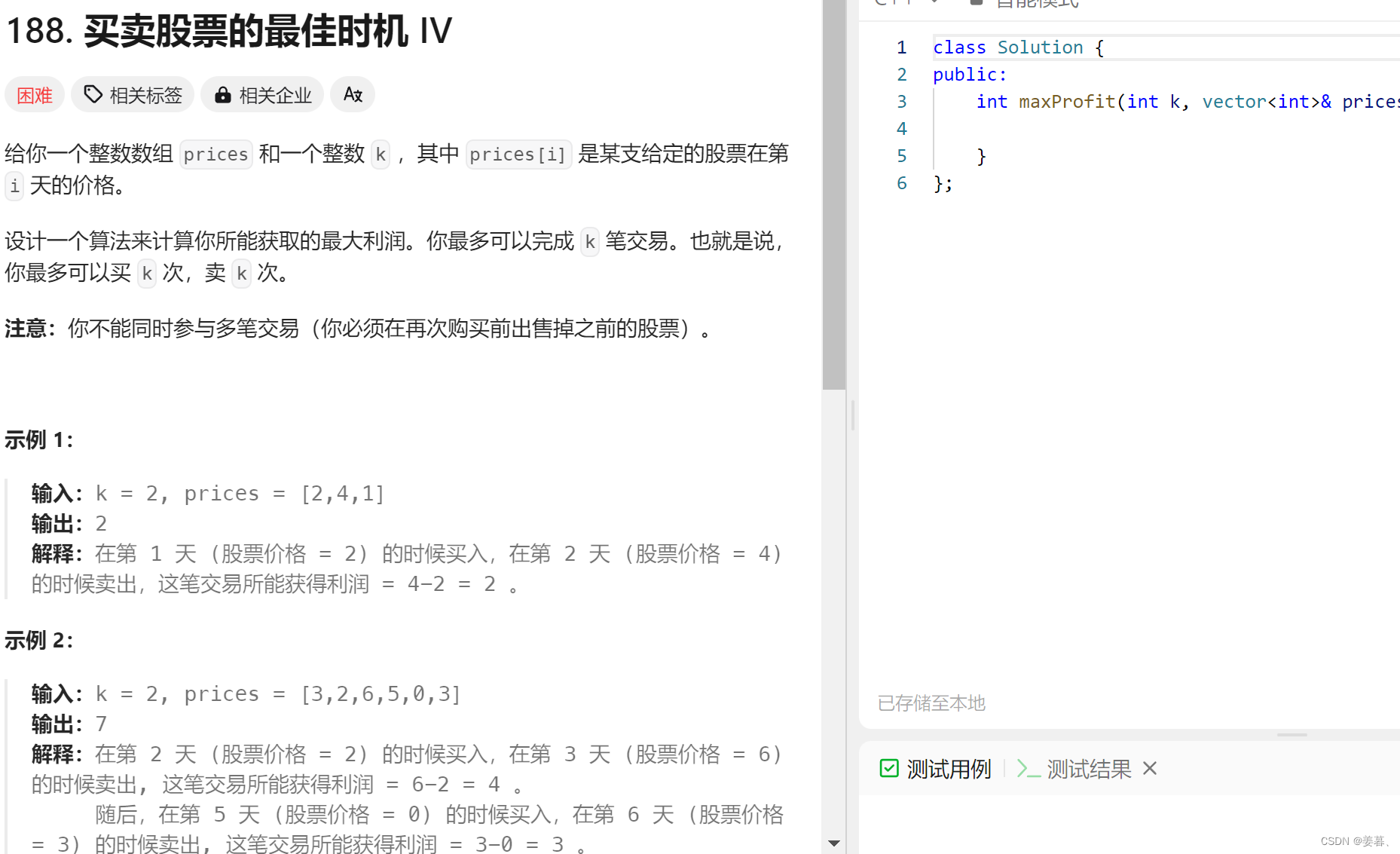
};9、买卖股票的最佳时机IV
本题跟买卖股票的最佳时机III的分析思路基本一模一样,但是本题多了一个细节问题,即优化时间复杂度



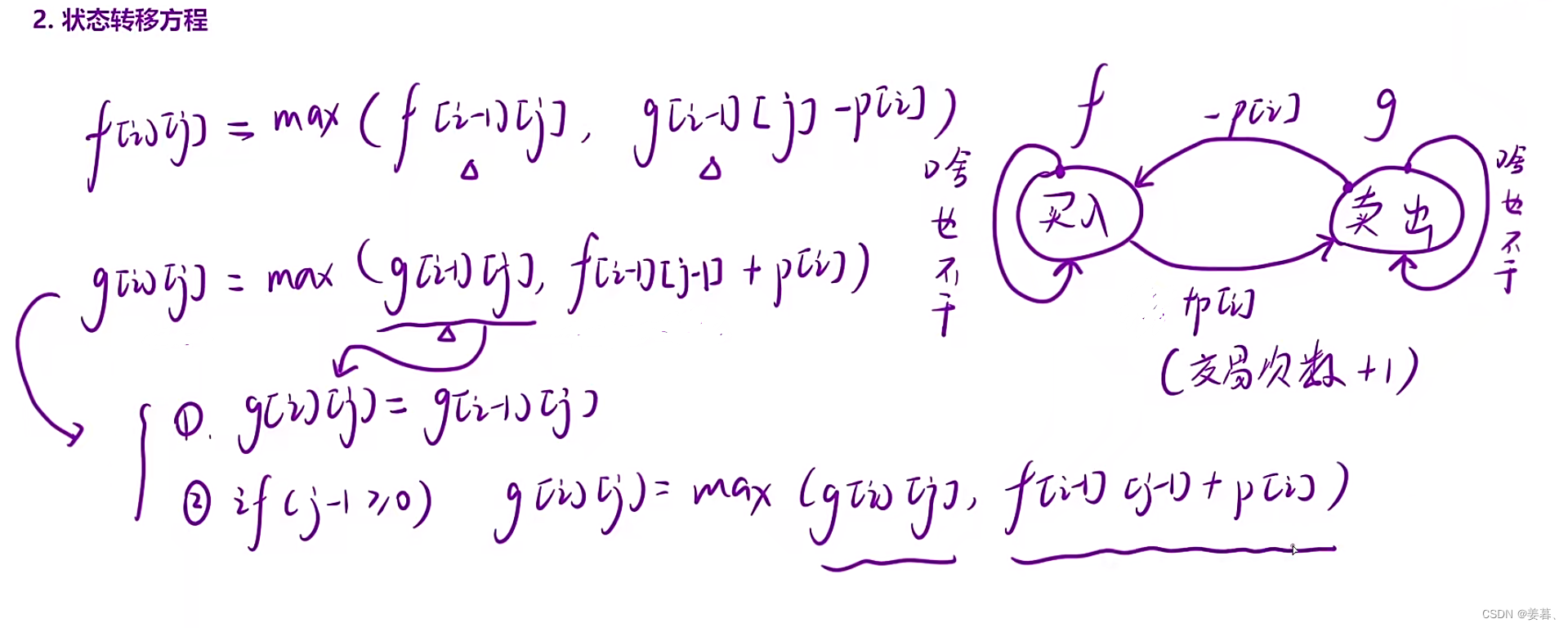


class Solution {
public:const int INF = 0x3f3f3f3f;int maxProfit(int k, vector<int>& prices) {int n = prices.size();k = min(k, n / 2);//处理细节问题vector<vector<int>> f(n, vector<int>(k + 1, -INF));auto g = f;f[0][0] = -prices[0], g[0][0] = 0;for (int i = 1; i < n; i++){//因为第一行已经初始化了,所以i从1开始for (int j = 0; j <= k; j++){f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i]);g[i][j] = g[i - 1][j];if (j - 1 >= 0)g[i][j] = max(g[i][j], f[i - 1][j - 1] + prices[i]);}}int ret = 0;for (int i = 0; i <= k; i++)ret = max(ret, g[n - 1][i]);return ret;}
};相关文章:

【动态规划精选题目】3、简单多状态模型
此动态规划系列主要讲解大约10个系列【后续持续更新】 本篇讲解简单多状态模型中的9道经典题,会在讲解题目同时给出AC代码 目录 1、按摩师 2、力扣198:打家劫舍1 3、打家劫舍II 4、删除并获得点数 5、 粉刷房子 6、力扣309:买卖股票的最佳时机含冷冻期 7、 买…...

软件测试/测试开发丨Python 虚拟环境及pip环境管理
venv 虚拟环境管理 venv 虚拟环境的优点 独立的 Python 环境,不会产生冲突有助于包的管理删除和卸载方便 venv 使用方法 创建虚拟环境 python3 -m venv test 激活虚拟环境 切换指定文件夹Windows:/Scripts/macOS:/bin/ 执行指令ÿ…...

Mybatis SQL构建器类 - SQL类
下面是一些例子: // Anonymous inner class public String deletePersonSql() {return new SQL() {{DELETE_FROM("PERSON");WHERE("ID #{id}");}}.toString(); }// Builder / Fluent style public String insertPersonSql() {String sql new…...

海云安亮相2023北京国际金融安全论坛,助力金融企业数字化转型降本增效
近日,2023北京国际金融安全论坛暨金融科技标准认证生态大会在北京金融安全产业园成功举办。深圳海云安网络安全技术有限公司(以下简称“海云安”)受邀参展亮相此次大会。海云安作为国内领先的金融科技服务商,展示了开发安全系列产…...
nodeJS搭建免费代理IP池爬取贴吧图片实战
之前用python写过爬虫,这次想试试nodeJS爬虫爬取贴吧图片,话不多说代码如下,爬取制定吧的前十页所有帖子里的图片 爬取贴吧图片脚本 你得提前创建一个images文件夹 const axios require("axios"); const cheerio require("…...
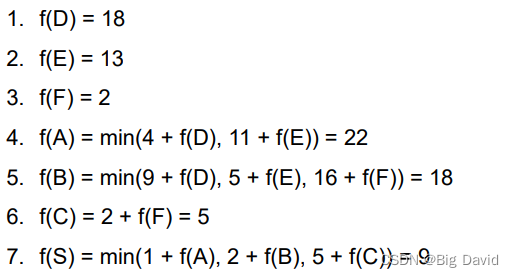
基于图搜索的自动驾驶规划算法 - BFS,Dijstra,A*
本文将讲解BFS,Dijstra,A*,动态规划的算法原理,不正之处望读者指正,希望有兴趣的读者能在评论区提出一些这些算法的面试考点,共同学习,一起进步 0 图论基础 图有三种:无向图、有向…...
Spring系列学习四、Spring数据访问
Spring数据访问 一、Spring中的JDBC模板介绍1、新建SpringBoot应用2、引入依赖:3、配置数据库连接,注入dbcTemplate对象,执行查询:4,测试验证: 二、整合MyBatis Plus1,在你的项目中添加MyBatis …...
)
HBase 创建不分裂的表 ( 禁止 Table Split )
注意:由于 HBase 版本众多,配置表的语法在不同版本上会有差异,本文介绍的配置方法是在 1.4.9 版本上测试的,使用 HBase 2.0 的版本需要核实并修改相关配置方法! 有时候,出于特殊需要,我们希望对…...

docker入门概念详解
本篇文章对docker的一些基础概念和周边概念进行了详细解释。帮助你可以很好的理解docker是用来干什么的,docker是怎么工作的。其中有docker所运用到的技术解释,docker的不同发展版本,dokcer的架构,docker的生态等等详解。希望本片…...

C++程序设计实践报告【格式】
C程序设计实践报告 原XX工业学院 C程序设计实践报告 题目: 专业: 学号: 姓名: 年 月 日 目录 一、绪…...

浅谈数据仓库运营
一、背景 企业每天都会产生大量的数据,随着时间增长,数据会呈现几何增长,尤其在系统基建基础好的公司。好的数据仓库需要提前规划和好的运营,才能支持企业的发展,为企业提供数据分析基础。 二、目标 提高数据仓库存储…...
系列六、Consul
一、Consul 1.1、概述 Consul是一套开源的分布式服务发现和配置管理系统,由HashiCorp公司用Go语言开发。他提供了微服务系统中的服务治理、配置中心、控制总线等功能。这些功能中的每一个功能都可以单独使用,也可以一起使用以构建全方位的服务网格&…...

Java集合/泛型篇----第一篇
系列文章目录 文章目录 系列文章目录前言一、ArrayList和linkedList的区别二、HashMap和HashTable的区别三、Collection包结构,与Collections的区别四、泛型常用特点前言 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站…...

集合使用注意事项
集合使用注意事项总结 集合判空 判断所有集合内部的元素是否为空,使用 isEmpty() 方法,而不是 size()0 的方式 这是因为 isEmpty() 方法的可读性更好,并且时间复杂度为 O(1)。 集合转 Map 在使用 java.util.stream.Collectors 类的 toMap()…...

什么是 JavaScript 中的 WeakMap
在 JavaScript 中,WeakMap 是一种特殊的 Map 数据结构,它允许将对象作为键,而且键值对是弱引用的关系。 与 Map 不同的是,WeakMap 的键只能是对象,不能是其他类型的值。同时,当键对象没有任何引用时&#…...
nodejs+vue+ElementUi农产品团购销售系统zto2c
目标是为了完成小区团购平台的设计和实现,在疫情当下的环境,方便小区业主购入生活所需,减小居民的生活压力 采用B/S模式架构系统,开发简单,只需要连接网络即可登录本系统,不需要安装任何客户端。开发工具采…...
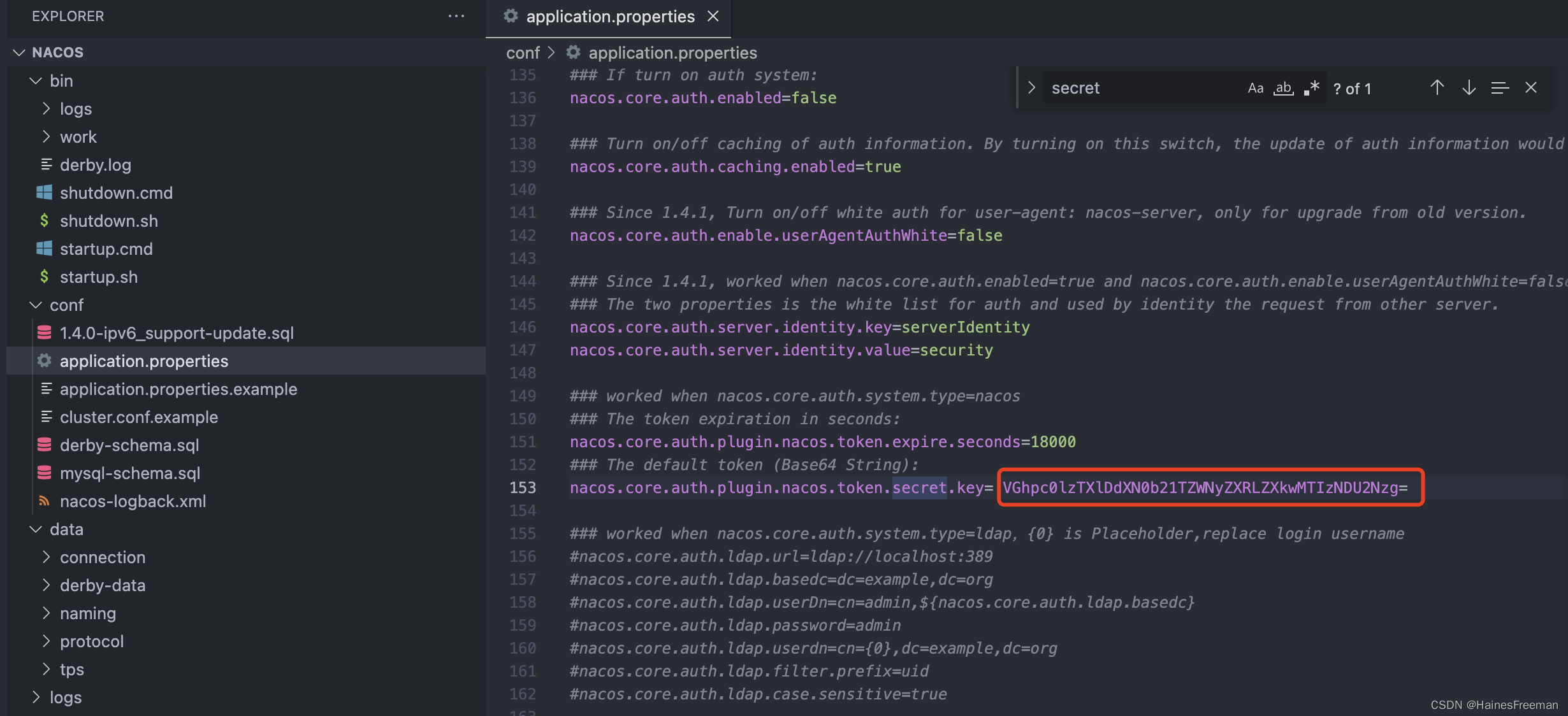
nacos入门篇001-安装与启动
1、下载zip包 我这里下载的是版本2.2.0 Nacos 快速开始 2、修改配置文件 2.1集群模式修改成单例模式 vi startup.sh 2.2 修改数据库配置信息 3、初始化数据库 3.1 创建db名称:db_nacos 3.2 执行mysql-schema.sql 3.3 执行完截图: 4、运行脚本启动 …...
WordPress主题大前端DUX v8.3源码下载
DUX主题8.3版本更新内容: 新增:Cloudflare Turnstile 免费验证功能 新增:子菜单页面模版,支持多级页面 新增:手机端文章内表格自动出现横向滚动条,可集体或单独设置滚动宽度 新增:标签云页面模版…...
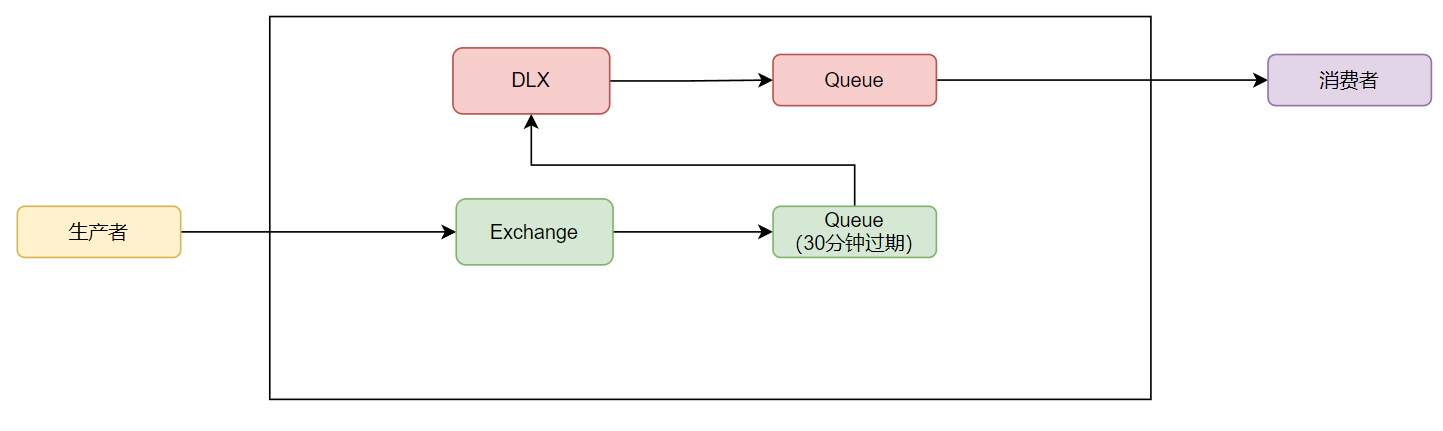
RabbitMQ之快速入门、上手
前言 学习一样新技术、新框架,最重要的是学习其思想、原理。即原理性思维。 如果是因为工作原因,需要快速上手RabbitMQ,本篇或许适合你。 核心概念 Connection:publisher/consumer 和 broker 之间的 TCP 连接Channel…...
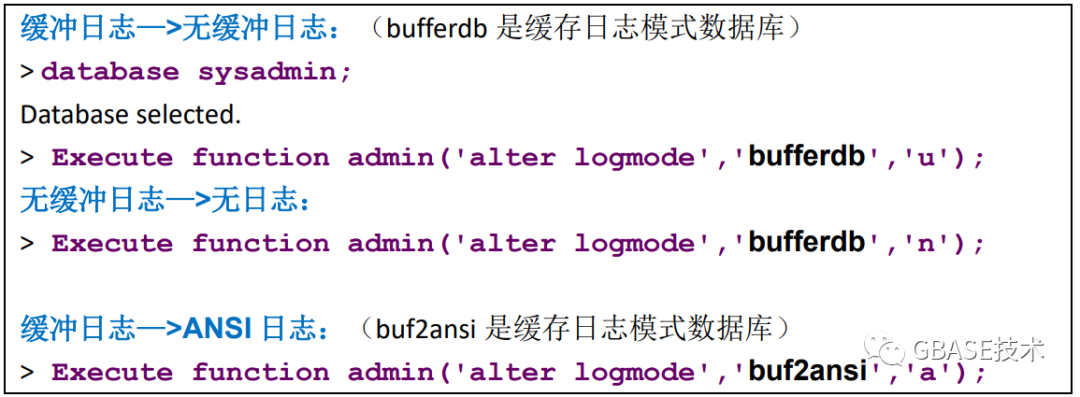
GBASE南大通用-GBase 8s数据库日志模式及切换
一、 GBase 8s数据库共有以下 4 种日志模式:无日志模式、缓冲日志模式、无缓冲日志模式、ANSI 模式。详细介绍如下: 1、无日志模式(Non logging): 采用无日志模式时,所有 DML 操作都不会被记录到日志中&…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

第八部分:阶段项目 6:构建 React 前端应用
现在,是时候将你学到的 React 基础知识付诸实践,构建一个简单的前端应用来模拟与后端 API 的交互了。在这个阶段,你可以先使用模拟数据,或者如果你的后端 API(阶段项目 5)已经搭建好,可以直接连…...

AxureRP-Pro-Beta-Setup_114413.exe (6.0.0.2887)
Name:3ddown Serial:FiCGEezgdGoYILo8U/2MFyCWj0jZoJc/sziRRj2/ENvtEq7w1RH97k5MWctqVHA 注册用户名:Axure 序列号:8t3Yk/zu4cX601/seX6wBZgYRVj/lkC2PICCdO4sFKCCLx8mcCnccoylVb40lP...

【大模型】RankRAG:基于大模型的上下文排序与检索增强生成的统一框架
文章目录 A 论文出处B 背景B.1 背景介绍B.2 问题提出B.3 创新点 C 模型结构C.1 指令微调阶段C.2 排名与生成的总和指令微调阶段C.3 RankRAG推理:检索-重排-生成 D 实验设计E 个人总结 A 论文出处 论文题目:RankRAG:Unifying Context Ranking…...

