数据挖掘 聚类度量
格式化之前的代码:
import numpy as np#计算
import pandas as pd#处理结构化表格
import matplotlib.pyplot as plt#绘制图表和可视化数据的函数,通常与numpy和pandas一起使用。
from sklearn import metrics#聚类算法的评估指标。
from sklearn.cluster import KMeans#K均值聚类算法
from hopkins_test import hopkins_statistic
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号data = pd.read_csv('city.txt')#读数据########################检测是否有类结构###################### h_value = hopkins_statistic(data.values) 评估数据集的聚类倾向性,越接近于 0.5 表示数据集具有良好的聚类倾向性,越接近于 1 表示数据集的聚类倾向性较差。########################判定是否有最优簇数目#####################SSE = []
for i in range(1, 11): # k取1-10,计算簇内误差平方和model = KMeans(n_clusters=i)#创建一个 KMeans 对象 model,使用当前的簇数量 i 初始化该对象model.fit(data)#对数据集 data 进行拟合和聚类。SSE.append(model.inertia_)#获取当前模型的簇内误差平方和,并将其添加到 SSE 列表中。
plt.plot(range(1, 11), SSE, marker='.')#plt.plot() 函数绘制折线图,横坐标为簇数量(1-10),纵坐标为簇内误差平方和(SSE)。
plt.xticks(ticks= range(1, 11))#设置横坐标刻度为 1-10
plt.xlabel('k值',)
plt.ylabel('簇内误差平方和SSE')
plt.show()########################确定最优簇数目#####################
opt = 0
for k in [5,6]:#遍历簇数量列表 [5, 6]kmeans_model = KMeans(n_clusters=k, random_state=1).fit(data)#创建一个 KMeans 对象 kmeans_model,使用当前的簇数量 k 和随机种子 random_state=1 初始化该对象,对数据集 data 进行拟合和聚类labels = kmeans_model.labels_#获取每个样本所属的簇标签value = metrics.silhouette_score(data, labels, metric='euclidean')#计算当前聚类结果的轮廓系数,其中指定使用欧氏距离作为度量方式。print(value)#打印输出当前轮廓系数的值if value >= opt:#如果当前轮廓系数大于等于 opt 变量的值,则更新 opt、opt_k 和 opt_labels 分别为当前轮廓系数、簇数量 k 和对应的簇标签。opt = value#opt 存储了最佳轮廓系数的值,opt_k 存储了具有最佳轮廓系数的簇数量,opt_labels 存储了对应的簇标签。opt_k = kopt_labels = labels########################聚类结果显示#####################colors = ['r', 'c', 'b', 'y', 'g']#创建一个颜色列表 colors,用于指定每个簇的颜色。
plt.figure()#创建一个新的图形窗口
for j in range(5):#遍历簇标签的取值范围(0-4)index_set = np.where(opt_labels == j)#获取属于当前簇标签的样本的索引集合。cluster = data.iloc[index_set]#使用这些索引从数据集 data 中提取属于当前簇的样本,并赋值给变量 clusterplt.scatter(cluster.iloc[:, 0], cluster.iloc[:, 1], c=colors[j], marker='.')#绘制当前簇的样本点,横坐标为 cluster 的第一列,纵坐标为 cluster 的第二列,颜色为 colors[j],标记为小圆点 '.'。plt.show()
格式化之后的代码:
import numpy as np # 计算
import pandas as pd # 处理结构化表格
import matplotlib.pyplot as plt # 绘制图表和可视化数据的函数,通常与numpy和pandas一起使用。
from sklearn import metrics # 聚类算法的评估指标。
from sklearn.cluster import KMeans # K均值聚类算法
from hopkins_test import hopkins_statisticplt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号data = pd.read_csv('city.txt') # 读数据########################检测是否有类结构###################### h_value = hopkins_statistic(data.values) 评估数据集的聚类倾向性,越接近于 0.5 表示数据集具有良好的聚类倾向性,越接近于 1 表示数据集的聚类倾向性较差。########################判定是否有最优簇数目#####################SSE = []
for i in range(1, 11): # k取1-10,计算簇内误差平方和model = KMeans(n_clusters=i) # 创建一个 KMeans 对象 model,使用当前的簇数量 i 初始化该对象model.fit(data) # 对数据集 data 进行拟合和聚类。SSE.append(model.inertia_) # 获取当前模型的簇内误差平方和,并将其添加到 SSE 列表中。
plt.plot(range(1, 11), SSE, marker='.') # plt.plot() 函数绘制折线图,横坐标为簇数量(1-10),纵坐标为簇内误差平方和(SSE)。
plt.xticks(ticks=range(1, 11)) # 设置横坐标刻度为 1-10
plt.xlabel('k值', )
plt.ylabel('簇内误差平方和SSE')
plt.show()########################确定最优簇数目#####################
opt = 0
for k in [5, 6]: # 遍历簇数量列表 [5, 6]kmeans_model = KMeans(n_clusters=k, random_state=1).fit(data) # 创建一个 KMeans 对象 kmeans_model,使用当前的簇数量 k 和随机种子 random_state=1 初始化该对象,对数据集 data 进行拟合和聚类labels = kmeans_model.labels_ # 获取每个样本所属的簇标签value = metrics.silhouette_score(data, labels, metric='euclidean') # 计算当前聚类结果的轮廓系数,其中指定使用欧氏距离作为度量方式。print(value) # 打印输出当前轮廓系数的值if value >= opt: # 如果当前轮廓系数大于等于 opt 变量的值,则更新 opt、opt_k 和 opt_labels 分别为当前轮廓系数、簇数量 k 和对应的簇标签。opt = value # opt 存储了最佳轮廓系数的值,opt_k 存储了具有最佳轮廓系数的簇数量,opt_labels 存储了对应的簇标签。opt_k = kopt_labels = labels########################聚类结果显示#####################colors = ['r', 'c', 'b', 'y', 'g'] # 创建一个颜色列表 colors,用于指定每个簇的颜色。
plt.figure() # 创建一个新的图形窗口
for j in range(5): # 遍历簇标签的取值范围(0-4)index_set = np.where(opt_labels == j) # 获取属于当前簇标签的样本的索引集合。cluster = data.iloc[index_set] # 使用这些索引从数据集 data 中提取属于当前簇的样本,并赋值给变量 clusterplt.scatter(cluster.iloc[:, 0], cluster.iloc[:, 1], c=colors[j],marker='.') # 绘制当前簇的样本点,横坐标为 cluster 的第一列,纵坐标为 cluster 的第二列,颜色为 colors[j],标记为小圆点 '.'。plt.show()
霍普金斯统计代码
格式化之前:
import numpy as np#计算
from sklearn.neighbors import NearestNeighbors#最近邻搜索的算法实现,可用于在数据集中查找最接近给定样本的邻居。
from sklearn.datasets import load_iris#load_iris函数是一个用于加载鸢尾花数据集的辅助函数
import pandas as pd#数据分析
from random import sample#随机抽样和洗牌操作
from numpy.random import uniform#均匀分布的随机数
def hopkins_statistic(X):#输入参数X是一个二维数组,表示原始数据集sample_size = int(X.shape[0]*0.05) #0.05 (5%) based on paper by Lawson and Jures #计算样本大小,占原始数据集大小的5%。这个样本将用于生成均匀随机样本。#原始数据空间的均匀随机样本X_uniform_random_sample = uniform(X.min(axis=0), X.max(axis=0) ,(sample_size , X.shape[1]))#X.min(axis=0)和X.max(axis=0)会计算原始数据集X每一列的最小值和最大值。这将返回一个包含每列最小值的一维数组和一个包含每列最大值的一维数组uniform函数将使用这些最小值和最大值来指定随机样本的取值范围。指定了生成的随机样本的形状,即一个元组(sample_size, X.shape[1]),其中sample_size表示样本大小,X.shape[1]表示每个样本的特征数。#从原始数据中随机抽取一个样本random_indices=sample(range(0, X.shape[0], 1), sample_size)#从原始数据集X中随机选择一个子集。具体而言,range(0, X.shape[0], 1)将返回一个从0到X.shape[0]的整数序列,步长为1。sample函数将从该序列中随机选择sample_size个不重复的整数,这些整数将用于从X中抽取对应的样本。X_sample = X[random_indices]#根据随机选择的索引从原始数据集中抽取一部分样本#初始化无监督学习器以实现NN搜索neigh = NearestNeighbors(n_neighbors=2)#NearestNeighbors是一个用于寻找最近邻的非监督学习算法。在这里,n_neighbors=2参数指定了要查找的最近邻的数量,即每个样本要找到的最近的两个邻居。nbrs=neigh.fit(X)#u_distances = 均匀随机样本的最近邻距离u_distances , u_indices = nbrs.kneighbors(X_uniform_random_sample , n_neighbors=2)#计算均匀随机样本X_uniform_random_sample在原始数据集X中的最近邻距离,并返回距离和对应的索引。这里将返回每个均匀随机样本的两个最近邻距离,其中第一个最近邻是样本本身,距离为0,因此只保留第二个最近邻的距离。u_distances = u_distances[: , 0] #到第一个最近邻居的距离#仅保留到第一个最近邻的距离#w_distances = 来自原始数据X的点样本的最近邻距离w_distances , w_indices = nbrs.kneighbors(X_sample , n_neighbors=2)#计算从原始数据集中抽取的样本X_sample的最近邻距离,并返回距离和对应的索引。同样,只保留第二个最近邻的距离。#到第二个最近邻居的距离(因为第一个邻居将是点本身,距离= 0)w_distances = w_distances[: , 1]#仅保留到第二个最近邻的距离u_sum = np.sum(u_distances)#计算均匀随机样本的最近邻距离之和w_sum = np.sum(w_distances)#计算来自原始数据集的样本的最近邻距离之和#计算并返回霍普金斯统计数据H = u_sum/ (u_sum + w_sum)#计算霍普金斯统计数据return H#返回计算得到的霍普金斯统计量
if __name__=="__main__":#if __name__=="__main__":是一个条件语句,它判断当前脚本是否作为主程序直接运行。只有当脚本作为主程序运行时,才会执行if语句块中的代码。iris=load_iris().data#iris = load_iris().data加载了一个名为iris的数据集,数据集是鸢尾花数据集。.data属性返回数据集的特征部分。h_value=hopkins_statistic(iris)#h_value = hopkins_statistic(iris)调用了名为hopkins_statistic的函数,计算了数据集的Hopkins统计量,并将结果赋值给变量h_value。
格式化之后的代码:
import numpy as np # 计算
from sklearn.neighbors import NearestNeighbors # 最近邻搜索的算法实现,可用于在数据集中查找最接近给定样本的邻居。
from sklearn.datasets import load_iris # load_iris函数是一个用于加载鸢尾花数据集的辅助函数
import pandas as pd # 数据分析
from random import sample # 随机抽样和洗牌操作
from numpy.random import uniform # 均匀分布的随机数def hopkins_statistic(X): # 输入参数X是一个二维数组,表示原始数据集sample_size = int(X.shape[0] * 0.05) # 0.05 (5%) based on paper by Lawson and Jures #计算样本大小,占原始数据集大小的5%。这个样本将用于生成均匀随机样本。# 原始数据空间的均匀随机样本X_uniform_random_sample = uniform(X.min(axis=0), X.max(axis=0), (sample_size, X.shape[1])) # X.min(axis=0)和X.max(axis=0)会计算原始数据集X每一列的最小值和最大值。这将返回一个包含每列最小值的一维数组和一个包含每列最大值的一维数组uniform函数将使用这些最小值和最大值来指定随机样本的取值范围。指定了生成的随机样本的形状,即一个元组(sample_size, X.shape[1]),其中sample_size表示样本大小,X.shape[1]表示每个样本的特征数。# 从原始数据中随机抽取一个样本random_indices = sample(range(0, X.shape[0], 1),sample_size) # 从原始数据集X中随机选择一个子集。具体而言,range(0, X.shape[0], 1)将返回一个从0到X.shape[0]的整数序列,步长为1。sample函数将从该序列中随机选择sample_size个不重复的整数,这些整数将用于从X中抽取对应的样本。X_sample = X[random_indices] # 根据随机选择的索引从原始数据集中抽取一部分样本# 初始化无监督学习器以实现NN搜索neigh = NearestNeighbors(n_neighbors=2) # NearestNeighbors是一个用于寻找最近邻的非监督学习算法。在这里,n_neighbors=2参数指定了要查找的最近邻的数量,即每个样本要找到的最近的两个邻居。nbrs = neigh.fit(X)# u_distances = 均匀随机样本的最近邻距离u_distances, u_indices = nbrs.kneighbors(X_uniform_random_sample,n_neighbors=2) # 计算均匀随机样本X_uniform_random_sample在原始数据集X中的最近邻距离,并返回距离和对应的索引。这里将返回每个均匀随机样本的两个最近邻距离,其中第一个最近邻是样本本身,距离为0,因此只保留第二个最近邻的距离。u_distances = u_distances[:, 0] # 到第一个最近邻居的距离#仅保留到第一个最近邻的距离# w_distances = 来自原始数据X的点样本的最近邻距离w_distances, w_indices = nbrs.kneighbors(X_sample,n_neighbors=2) # 计算从原始数据集中抽取的样本X_sample的最近邻距离,并返回距离和对应的索引。同样,只保留第二个最近邻的距离。# 到第二个最近邻居的距离(因为第一个邻居将是点本身,距离= 0)w_distances = w_distances[:, 1] # 仅保留到第二个最近邻的距离u_sum = np.sum(u_distances) # 计算均匀随机样本的最近邻距离之和w_sum = np.sum(w_distances) # 计算来自原始数据集的样本的最近邻距离之和# 计算并返回霍普金斯统计数据H = u_sum / (u_sum + w_sum) # 计算霍普金斯统计数据return H # 返回计算得到的霍普金斯统计量if __name__ == "__main__": # if __name__=="__main__":是一个条件语句,它判断当前脚本是否作为主程序直接运行。只有当脚本作为主程序运行时,才会执行if语句块中的代码。iris = load_iris().data # iris = load_iris().data加载了一个名为iris的数据集,数据集是鸢尾花数据集。.data属性返回数据集的特征部分。h_value = hopkins_statistic(iris) # h_value = hopkins_statistic(iris)调用了名为hopkins_statistic的函数,计算了数据集的Hopkins统计量,并将结果赋值给变量h_value。相关文章:

数据挖掘 聚类度量
格式化之前的代码: import numpy as np#计算 import pandas as pd#处理结构化表格 import matplotlib.pyplot as plt#绘制图表和可视化数据的函数,通常与numpy和pandas一起使用。 from sklearn import metrics#聚类算法的评估指标。 from sklearn.clust…...
[Angular] 笔记 24:ngContainer vs. ngTemplate vs. ngContent
请说明 Angular 中 ngContainer, ngTemplate 和 ngContent 这三者之间的区别。 chatgpt 回答: 这三个在 Angular 中的概念是关于处理和组织视图的。 1. ngContainer: ngContainer 是一个虚拟的 HTML 容器,它本身不会在最终渲染…...

❀My排序算法学习之插入排序❀
目录 插入排序(Insertion Sort):) 一、定义 二、基本思想 三、示例 时间复杂度 空间复杂度 bash C++ 四、稳定性分析...

【算法题】30. 串联所有单词的子串
题目 给定一个字符串 s 和一个字符串数组 words。 words 中所有字符串 长度相同。 s 中的 串联子串 是指一个包含 words 中所有字符串以任意顺序排列连接起来的子串。 例如,如果 words ["ab","cd","ef"], 那么 "…...

SAP-FI模块 处理自动生成会计凭证增强
ENHANCEMENT 2 ZEHENC_SAPMF05A. "active version * FI 20221215:固定资产业务过渡科目摘要增强功能 WAIT UP TO 1 SECONDS.READ TABLE xbseg WITH KEY hkont 1601990001. IF sy-subrc 0.DATA: lt_bkdf TYPE TABLE OF bkdf,lt_bkpf TYPE TABLE OF bkpf,…...
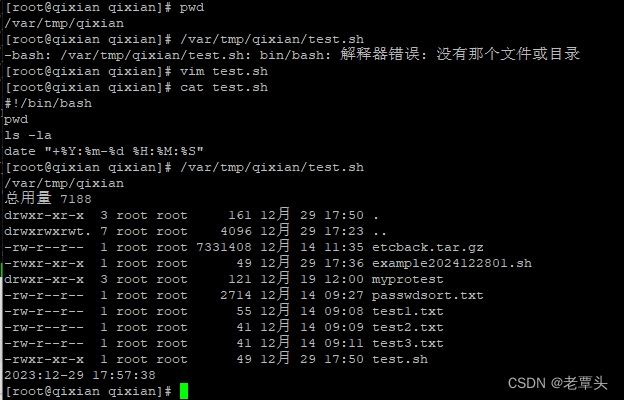
Shell脚本-bin/bash: 解释器错误: 没有那个文件或目录-完整路径执行-“/”引发的脑裂
引起该不适的一种可能以及解决方案,网上较多,比如: 但按以上方式操作,并经过查看,发现仍然未能解决问题。 因为两种方式执行,有一种能成功,有一种不能,刚开始未怀疑是文件问题&…...
详细使用)
React MUI(版本v5.15.2)详细使用
使用React MUI(版本v5.15.2)的详细示例。请注意,由于版本可能会有所不同,因此建议您查阅官方文档以获取最新的信息和示例。但是,我将根据我的知识库为您提供一些基本示例。 首先,确保您已经按照之前的说明…...
用CSS中的动画效果做一个转动的表
<!DOCTYPE html> <html lang"en"><head><meta charset"utf-8"><title></title><style>*{margin:0;padding:0;} /*制作表的样式*/.clock{width: 500px;height: 500px;margin:0 auto;margin-top:100px;border-rad…...
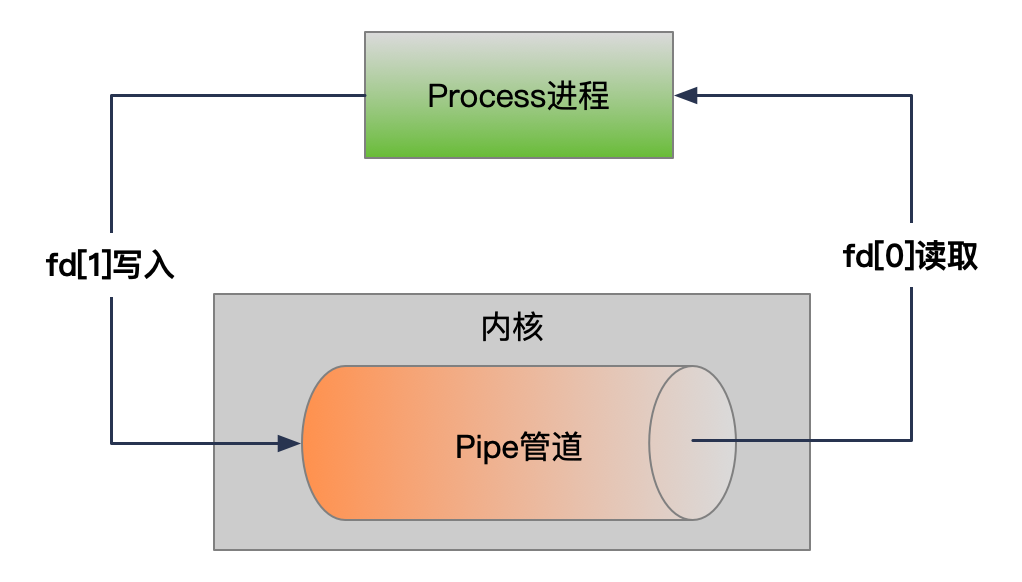
【linux】Linux管道的原理与使用场景
Linux管道是Linux命令行界面中一种强大的工具,它允许用户将多个命令链接起来,使得一个命令的输出可以作为另一个命令的输入。这种机制使得我们可以创建复杂的命令链,并在处理数据时提供了极大的灵活性。在本文中,我们将详细介绍Li…...

nvidia jetson xavier nx developer kit version emmc版重装系统
一、将开发板上的外置硬盘取下来格式化 二、在双系统ubuntu安装SDK Manager(.deb文件) SDK Manager | NVIDIA Developer sudo apt install ./sdkmanager_1.9.2-10884_amd64.deb 报错直接百度错误,执行相应命令即可 三、 运行SDK Manager …...

命令模式-实例使用
未使用命令模式的UML 使用命令模式后的UML public abstract class Command {public abstract void execute(); }public class Invoker {private Command command;/*** 为功能键注入命令* param command*/public void setCommand(Command command) {this.command command;}/***…...

将网页变身移动应用:网址封装成App的完全指南
什么是网址封装? 网址封装是一个将你的网站或网页直接嵌入到一个原生应用容器中的过程。用户可以通过下载你的App来访问网站,而无需通过浏览器。这种方式不仅提升了用户体验,还可利用移动设备的功能,如推送通知和硬件集成。 小猪…...
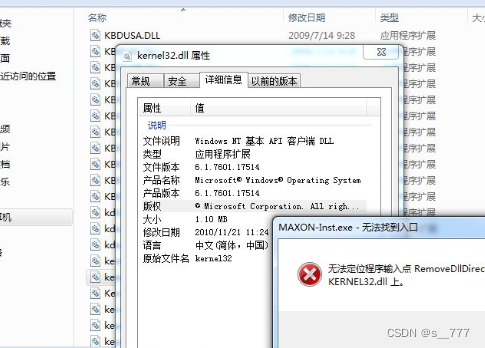
探讨kernel32.dll文件是什么,有效解决kernel32.dll丢失
在使用电脑时,你是否遇到过kernel32.dll丢失的困扰?面对这个问题,我们需要及时去解决kernel32.dll丢失的问题。接下来,我们将深入探讨kernel32.dll的功能以及其在操作系统和应用程序中的具体应用领域,相信这将对你解决…...
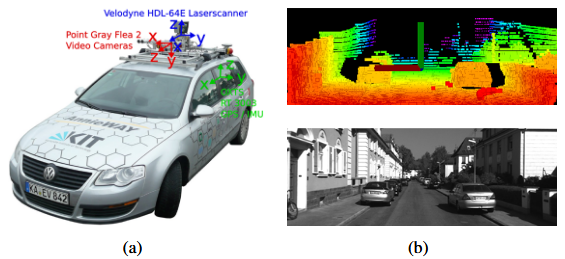
LOAM: Lidar Odometry and Mapping in Real-time 论文阅读
论文链接 LOAM: Lidar Odometry and Mapping in Real-time 0. Abstract 提出了一种使用二维激光雷达在6自由度运动中的距离测量进行即时测距和建图的方法 距离测量是在不同的时间接收到的,并且运动估计中的误差可能导致生成的点云的错误配准 本文的方法在不需要高…...
如何使用Docker将.Net6项目部署到Linux服务器(三)
目录 四 安装nginx 4.1 官网下载nginx 4.2 下载解压安装nginx 4.3 进行configure 4.4 执行make 4.5 查看nginx是否安装成功 4.6 nginx的一些常用命令 4.6.1 启动nginx 4.6.2 通过命令查看nginx是否启动成功 4.6.3 关闭Nginx 4.6.5 重启Nginx 4.6.6 杀掉所有Nginx进程 4.…...
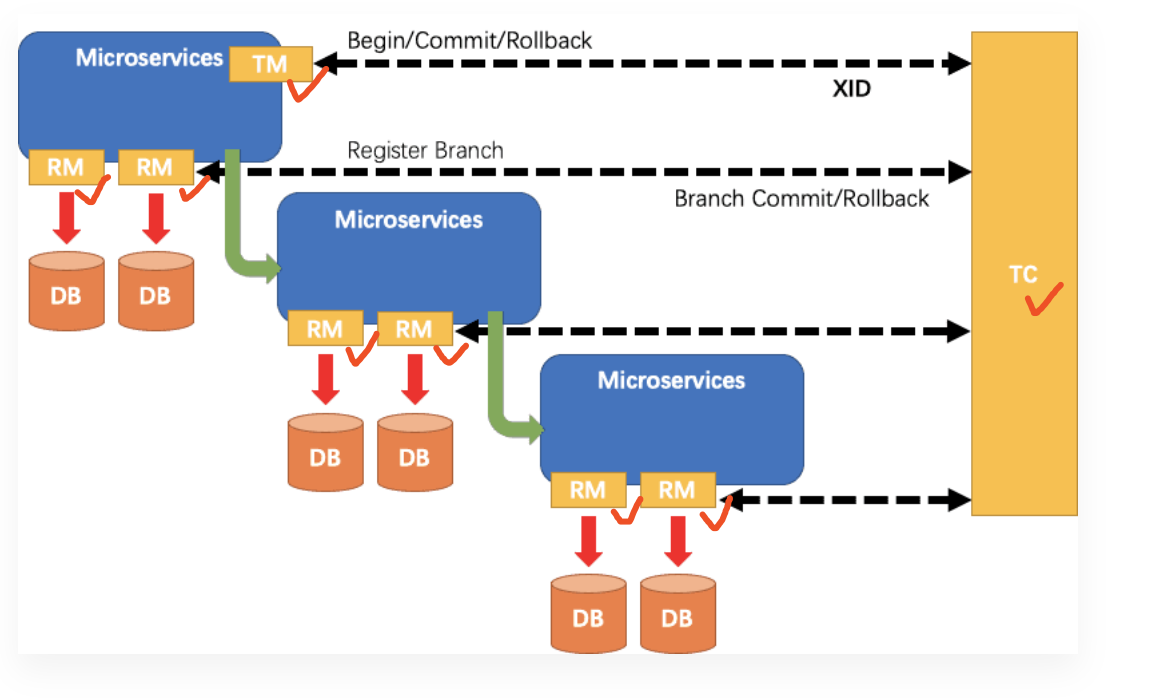
《Spring Cloud学习笔记:分布式事务Seata》
解决分布式事务的方案有很多,但实现起来都比较复杂,因此我们一般会使用开源的框架来解决分布式事务问题。 在众多的开源分布式事务框架中,功能最完善、使用最多的就是阿里巴巴在2019年开源的Seata了。 1. 初识Seata Seata是 2019 年 1 月…...
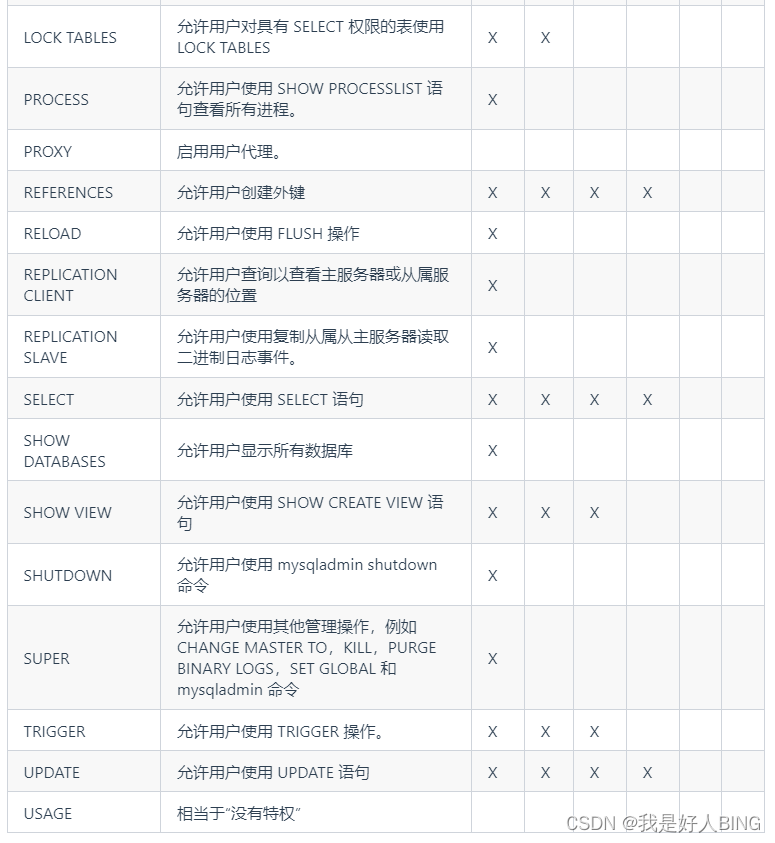
MySQL:权限控制
要授予用户帐户权限,可以用GRANT命令。有撤销用户的权限,可以用REVOKE命令。这里以 MySQl 为例,介绍权限控制实际应用。 GRANT授予权限语法: GRANT privilege,[privilege],.. ON privilege_level TO user [IDENTIFIED BY passwo…...

安全生产知识竞赛活动方案
为进一步普及安全生产法律法规知识,增强安全意识,提高安全技能,经研究,决定举办以“加强安全法治、保障安全生产”为主题的新修订《安全生产法》知识竞赛活动,现将有关事项通知如下: 一、活动时间…...

2023 IoTDB Summit:天谋科技 CTO 乔嘉林《IoTDB 企业版 V1.3: 时序数据管理一站式解决方案》...
12 月 3 日,2023 IoTDB 用户大会在北京成功举行,收获强烈反响。本次峰会汇集了超 20 位大咖嘉宾带来工业互联网行业、技术、应用方向的精彩议题,多位学术泰斗、企业代表、开发者,深度分享了工业物联网时序数据库 IoTDB 的技术创新…...

LangChain.js 实战系列:如何统计大模型使用的 token 使用量和花费
📝 LangChain.js 是一个快速开发大模型应用的框架,它提供了一系列强大的功能和工具,使得开发者能够更加高效地构建复杂的应用程序。LangChain.js 实战系列文章将介绍在实际项目中使用 LangChain.js 时的一些方法和技巧。 统计调用大模型的 to…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...
