模式识别与机器学习-无监督学习-聚类
无监督学习-聚类
- 监督学习&无监督学习
- K-means
- K-means聚类的优点:
- K-means的局限性:
- 解决方案:
- 高斯混合模型(Gaussian Mixture Models,GMM)
- 多维高斯分布的概率密度函数:
- 高斯混合模型(Gaussian Mixture Model,GMM)
- 模型形式:
- EM算法迭代过程:
- K-means 与 高斯混合模型(GMM)的对比:
- K-means:
- 高斯混合模型(GMM):
- 高斯混合模型(GMM)的优缺点:
- 优点:
- 缺点:
- 选择应用场景:
- 层次聚类
- 簇之间的相似性度量
- 最小距离
- 最大距离
- 平均距离
- 中心点距离
- 凝聚聚类过程:
- DBSCAN
- DBSCAN算法步骤:
- DBSCAN的特点:
- 参数说明:
- 优势与局限性:
- 优势:
- 局限性:
- 例题
谨以此博客作为复习期间的记录
监督学习&无监督学习
监督学习和无监督学习是机器学习中两种基本的学习范式。
-
监督学习:
- 定义:监督学习是一种机器学习范式,在这种范式中,模型通过已标记的训练数据进行训练,每个训练样本都有一个标签或目标值。
- 特点:模型在学习过程中使用输入数据与其对应的已知输出(标签或目标值)之间的关系,目的是学习从输入到输出的映射关系,以便对新的未知数据做出准确的预测或分类。
- 优点:
- 可以利用已知的标签信息来进行精确的预测或分类。
- 在训练过程中可以评估模型的性能,并进行调整和改进。
- 适用于大多数真实世界的问题,如图像识别、语音识别、自然语言处理等。
- 缺点:
- 需要大量标记好的训练数据,数据标记成本高。
- 对于某些问题,标签数据可能不容易获得或标记。
-
无监督学习:
- 定义:无监督学习是一种机器学习方法,其中模型根据未标记的数据进行学习,没有对应的目标输出。
- 特点:在无监督学习中,模型试图从数据中发现隐藏的模式、结构或特征,而不需要预先定义的输出标签。
- 优点:
- 可以发现数据中的潜在结构、关联和规律,有助于理解数据本身。
- 适用于数据探索和降维等任务。
- 不需要标签,因此不受标签获取成本的影响。
- 缺点:
- 对于一些任务,无法直接量化或验证模型学到的信息。
- 在训练过程中难以衡量模型的性能。
K-means

K-means聚类的优点:
- 简单快速:K-means是一种直观且易于实现的聚类算法,计算效率高,适用于大规模数据集。
- 可扩展性:对于大规模数据,K-means算法具有良好的可扩展性和高效性。
- 对高斯分布接近的簇效果较好:当簇近似服从高斯分布时,K-means算法的聚类效果较好。
K-means的局限性:
- 硬划分数据:K-means对数据点进行硬划分,即每个数据点只能属于一个簇,当数据存在噪声或异常值时,可能会导致点被错误分配到不合适的簇中。
- 对簇形状和大小的假设:K-means假设簇是球形的,并且每个簇的概率相等,这在某些场景下可能不符合实际情况。

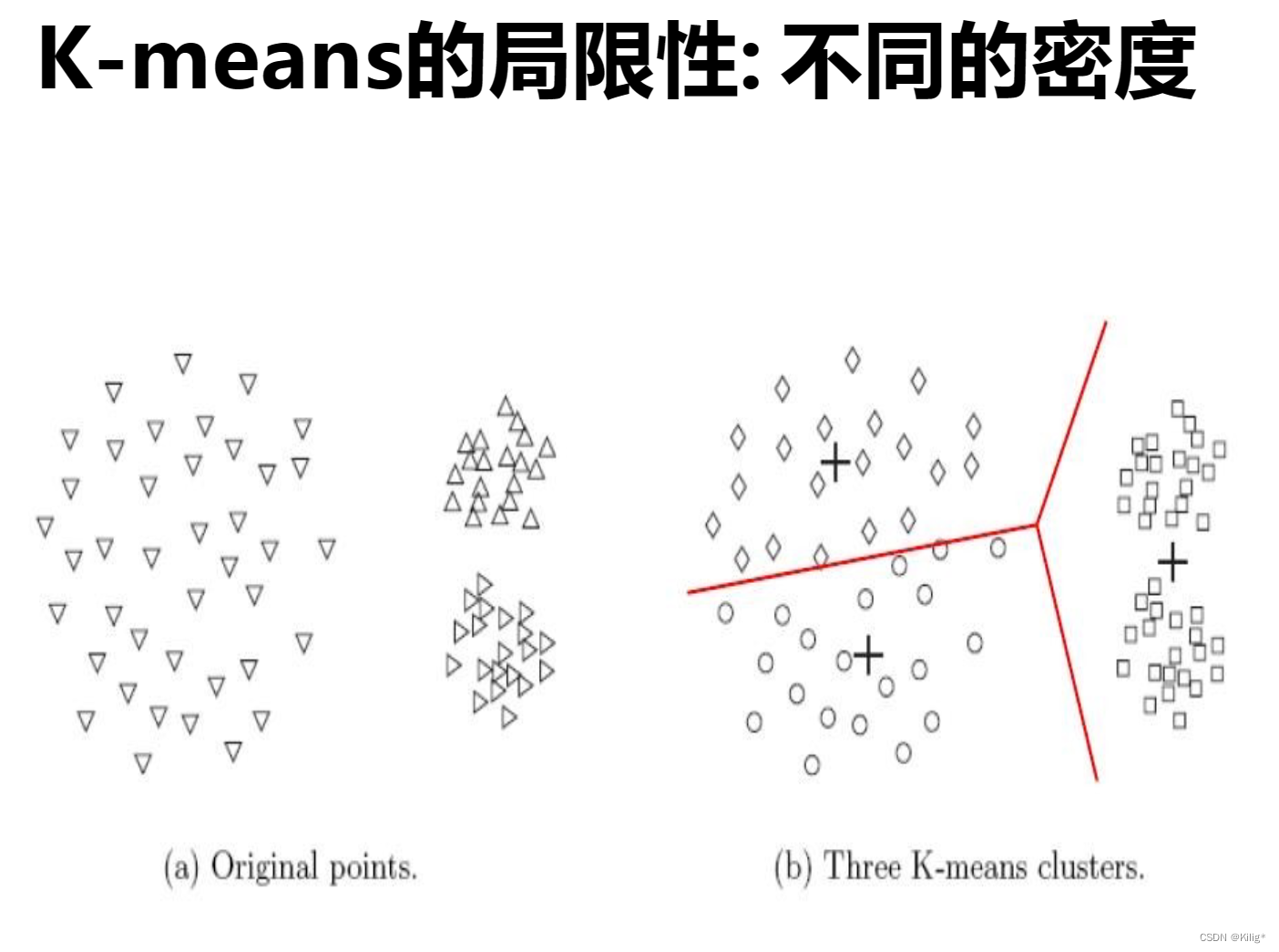
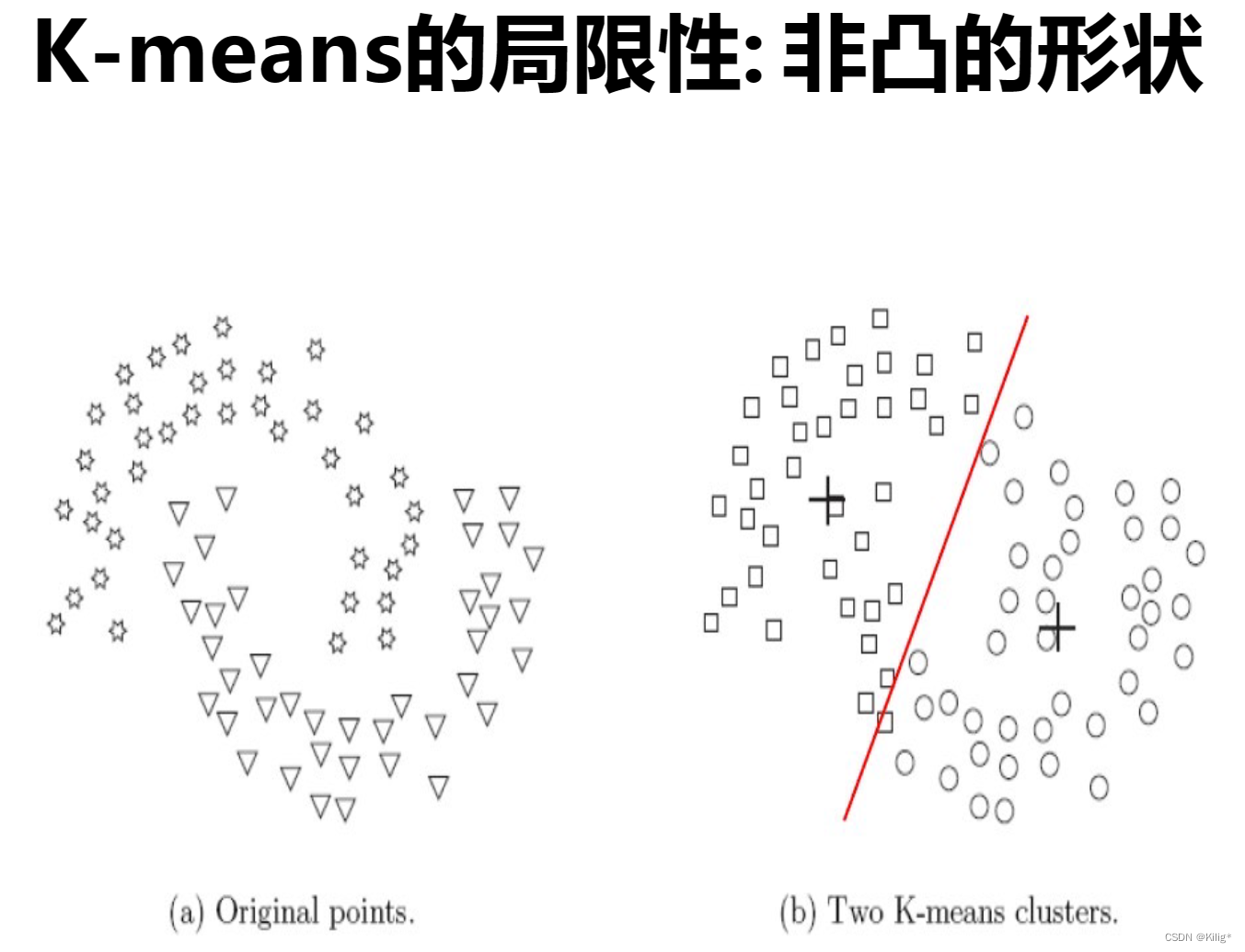
解决方案:
针对K-means的局限性,可以采用以下解决方案:
- 软聚类方法:使用软聚类方法,如高斯混合模型(Gaussian Mixture Models,GMM),允许数据点以一定的概率属于不同的簇,而不是强制性地将其分配到唯一的簇。
- 采用不同形状的簇:对非球形簇结构,可以考虑使用其他形式的聚类算法,如密度聚类(DBSCAN)等,这些算法对数据的形状和密度分布没有特定的假设。
高斯混合模型(Gaussian Mixture Models,GMM)
多维高斯分布的概率密度函数:
对于一个 D D D 维的随机向量 x = ( x 1 , x 2 , … , x D ) T \mathbf{x} = (x_1, x_2, \dots, x_D)^T x=(x1,x2,…,xD)T,其多维高斯分布的概率密度函数可以表示为:
N ( x ∣ μ , Σ ) = 1 ( 2 π ) D / 2 ∣ Σ ∣ 1 / 2 exp ( − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) ) \mathcal{N}(\mathbf{x}|\boldsymbol{\mu}, \boldsymbol{\Sigma}) = \frac{1}{(2\pi)^{D/2} |\boldsymbol{\Sigma}|^{1/2}} \exp \left(-\frac{1}{2} (\mathbf{x} - \boldsymbol{\mu})^T \boldsymbol{\Sigma}^{-1} (\mathbf{x} - \boldsymbol{\mu})\right) N(x∣μ,Σ)=(2π)D/2∣Σ∣1/21exp(−21(x−μ)TΣ−1(x−μ))
其中,
- μ = ( μ 1 , μ 2 , … , μ D ) T \boldsymbol{\mu} = (\mu_1, \mu_2, \dots, \mu_D)^T μ=(μ1,μ2,…,μD)T 是均值向量,表示随机向量每个维度的均值。
- Σ \boldsymbol{\Sigma} Σ 是协方差矩阵,表示随机向量各维度之间的协方差。
- ∣ Σ ∣ |\boldsymbol{\Sigma}| ∣Σ∣ 是协方差矩阵的行列式。
- T ^T T 表示向量的转置。
- exp ( ⋅ ) \exp(\cdot) exp(⋅) 是自然指数函数。
高斯混合模型(Gaussian Mixture Model,GMM)
模型形式:
假设有 N N N 个数据点 x 1 , x 2 , … , x N \mathbf{x}_1, \mathbf{x}_2, \dots, \mathbf{x}_N x1,x2,…,xN,GMM 的概率密度函数可表示为:
p ( x ) = ∑ k = 1 K π k N ( x ∣ μ k , Σ k ) p(\mathbf{x}) = \sum_{k=1}^{K} \pi_k \mathcal{N}(\mathbf{x}|\boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k) p(x)=k=1∑KπkN(x∣μk,Σk)
其中,
- K K K 是高斯分布的数量(聚类数目);
- π k \pi_k πk 是第 k k k 个高斯分布的权重,满足 ∑ k = 1 K π k = 1 \sum_{k=1}^{K} \pi_k = 1 ∑k=1Kπk=1;
- N ( x ∣ μ k , Σ k ) \mathcal{N}(\mathbf{x}|\boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k) N(x∣μk,Σk) 是多维高斯分布密度函数, μ k \boldsymbol{\mu}_k μk 是第 k k k 个高斯分布的均值向量, Σ k \boldsymbol{\Sigma}_k Σk 是其协方差矩阵。
EM算法迭代过程:
- 初始化:随机初始化模型参数(各高斯分布的均值、协方差矩阵和权重)。
- E步骤(Expectation):
- 计算每个数据点 x n \mathbf{x}_n xn 属于每个高斯分布的后验概率,即第 k k k 个高斯分布生成第 n n n 个数据点的概率:
γ ( z n k ) = π k N ( x n ∣ μ k , Σ k ) ∑ j = 1 K π j N ( x n ∣ μ j , Σ j ) \gamma(z_{nk}) = \frac{\pi_k \mathcal{N}(\mathbf{x}_n|\boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k)}{\sum_{j=1}^{K} \pi_j \mathcal{N}(\mathbf{x}_n|\boldsymbol{\mu}_j, \boldsymbol{\Sigma}_j)} γ(znk)=∑j=1KπjN(xn∣μj,Σj)πkN(xn∣μk,Σk)
- 计算每个数据点 x n \mathbf{x}_n xn 属于每个高斯分布的后验概率,即第 k k k 个高斯分布生成第 n n n 个数据点的概率:
- M步骤(Maximization):
- 重新估计参数:
- 更新每个高斯分布的权重 π k \pi_k πk:
π k = 1 N ∑ n = 1 N γ ( z n k ) \pi_k = \frac{1}{N} \sum_{n=1}^{N} \gamma(z_{nk}) πk=N1n=1∑Nγ(znk) - 更新每个高斯分布的均值 μ k \boldsymbol{\mu}_k μk:
μ k = ∑ n = 1 N γ ( z n k ) x n ∑ n = 1 N γ ( z n k ) \boldsymbol{\mu}_k = \frac{\sum_{n=1}^{N} \gamma(z_{nk})\mathbf{x}_n}{\sum_{n=1}^{N} \gamma(z_{nk})} μk=∑n=1Nγ(znk)∑n=1Nγ(znk)xn - 更新每个高斯分布的协方差矩阵 Σ k \boldsymbol{\Sigma}_k Σk:
Σ k = ∑ n = 1 N γ ( z n k ) ( x n − μ k ) ( x n − μ k ) T ∑ n = 1 N γ ( z n k ) \boldsymbol{\Sigma}_k = \frac{\sum_{n=1}^{N} \gamma(z_{nk})(\mathbf{x}_n - \boldsymbol{\mu}_k)(\mathbf{x}_n - \boldsymbol{\mu}_k)^T}{\sum_{n=1}^{N} \gamma(z_{nk})} Σk=∑n=1Nγ(znk)∑n=1Nγ(znk)(xn−μk)(xn−μk)T
- 更新每个高斯分布的权重 π k \pi_k πk:
- 重新估计参数:
- 重复迭代:重复执行E步骤和M步骤,直到模型参数收敛或达到预设的迭代次数。
在EM算法中,E步骤计算数据点属于每个高斯分布的后验概率,M步骤根据这些后验概率重新估计模型参数,迭代更新直至收敛。这个过程旨在最大化观测数据的似然函数,使得模型能够更好地拟合数据。
K-means 与 高斯混合模型(GMM)的对比:
K-means:
- 硬聚类算法:每个数据点仅属于一个簇。
- 假设:假定簇为球形,并对数据进行硬划分。
- 速度快:简单且计算效率高,适用于大规模数据集。
高斯混合模型(GMM):
- 软聚类算法:允许一个数据点以一定概率分配到不同的聚类中心。
- 假设:允许簇有不同形状和大小,并用高斯分布建模数据分布。
- 灵活性:适用于更广泛的数据形状和分布。
- 更复杂的模型:与K-means相比,GMM具有更复杂的模型和参数(均值、协方差、权重)。
高斯混合模型(GMM)的优缺点:
优点:
- 灵活性:对数据分布的假设更加灵活,可以拟合各种形状和大小的簇。
- 软聚类:允许数据以一定概率属于不同的聚类中心,更符合实际场景。
- 能量表达能力强:GMM是一个强大的建模工具,能够捕获数据中的复杂关系。
缺点:
- 计算复杂度高:相比于K-means,GMM具有更高的计算复杂度,特别是在高维数据上。
- 对初始值敏感:GMM对于初始参数值敏感,不同的初始值可能会导致不同的聚类结果。
- 可能陷入局部最优解:迭代优化过程可能陷入局部最优解,影响模型的效果。
选择应用场景:
- 如果数据集具有明显的簇结构、数据分布近似球形,并且对计算速度要求较高,K-means可能是一个不错的选择。
- 如果数据集具有复杂的形状、大小和分布,或者需要更丰富的数据建模,GMM可能更适合。
- 通常,可以根据数据的特点和任务的需求来选择适合的聚类算法。
层次聚类
簇之间的相似性度量
最小距离
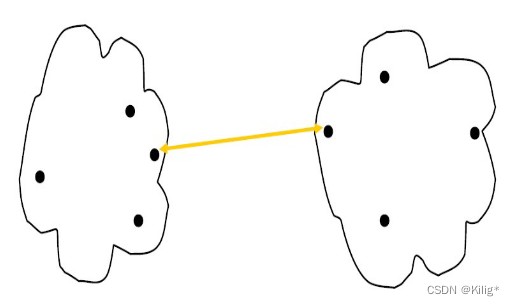
适合发现凸型簇或者非等向性的簇,对异常值不敏感。它衡量的是两个簇中最近的两个数据点的距离,所以在形成簇的过程中,容易受到离群点的影响。
最大距离
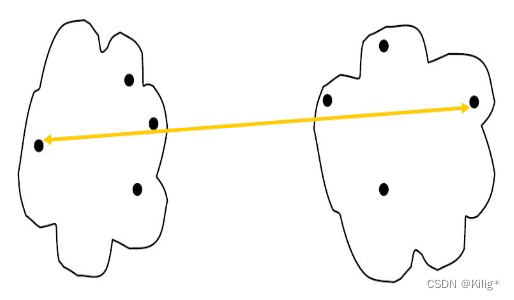
适合发现球状簇,能够很好地处理不同大小和密度的簇,对噪声和异常值比较稳健。它考虑的是两个簇中距离最远的两个数据点之间的距离,使得形成的簇间距离更大。
平均距离
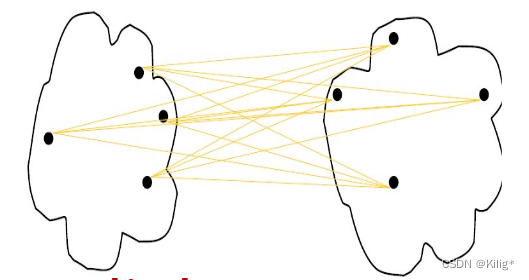
对各种类型的簇都相对适用,通常被视为对最小距离和最大距离的折衷方案。它计算两个簇中所有数据点之间的平均距离,能够平衡最小和最大距离法的影响。
中心点距离
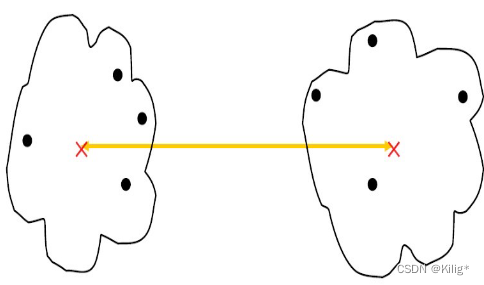
考虑簇之间的中心点(质心)之间的距离。这种方法对异常值相对较敏感,因为它完全依赖于簇的中心点,并且不适合非凸形状的簇。
层次聚类是一种按照层次结构组织的聚类方法,其主要思想是将数据点逐步合并或分割,形成一个层次化的聚类结构。层次聚类方法有两种主要的方法:凝聚聚类(Agglomerative Clustering)和分裂聚类(Divisive Clustering)。这里我将介绍凝聚聚类的过程。
凝聚聚类过程:
凝聚聚类是一种自底向上的聚类方法,其步骤如下:
-
初始化:
- 将每个数据点视为一个单独的簇。
-
计算相似度或距离:
- 计算所有数据点之间的相似度或距离(如欧氏距离、曼哈顿距离、相关系数等)。
-
合并最近的簇:
- 找到相似度或距离最小的两个簇,并将它们合并成一个新的簇。
- 合并簇的方式可以根据不同的距离度量方法来确定,比如单链接(single-linkage)、全链接(complete-linkage)、平均链接(average-linkage)等。
-
更新相似度矩阵:
- 更新相似度矩阵,重新计算新簇与其他簇之间的距离或相似度。
-
重复合并步骤:
- 重复进行合并步骤,不断合并距离最近的簇,直到满足某个停止条件(比如指定簇的数量、距离阈值等)。
-
构建聚类树(Dendrogram):
- 沿着合并过程,可以记录每次合并的簇以及它们的距离,构建层次聚类树或者称为树状图(Dendrogram)。
-
树状图的剪枝(可选):
- 可以根据业务需求或者树状图的结构,通过剪枝来选择最终的聚类结果,确定簇的数量。
凝聚聚类方法将每个数据点作为一个簇,然后通过不断合并最接近的簇,逐步形成层次化的聚类结构。最终,通过聚类树(Dendrogram)或剪枝得到最终的聚类结果。
DBSCAN
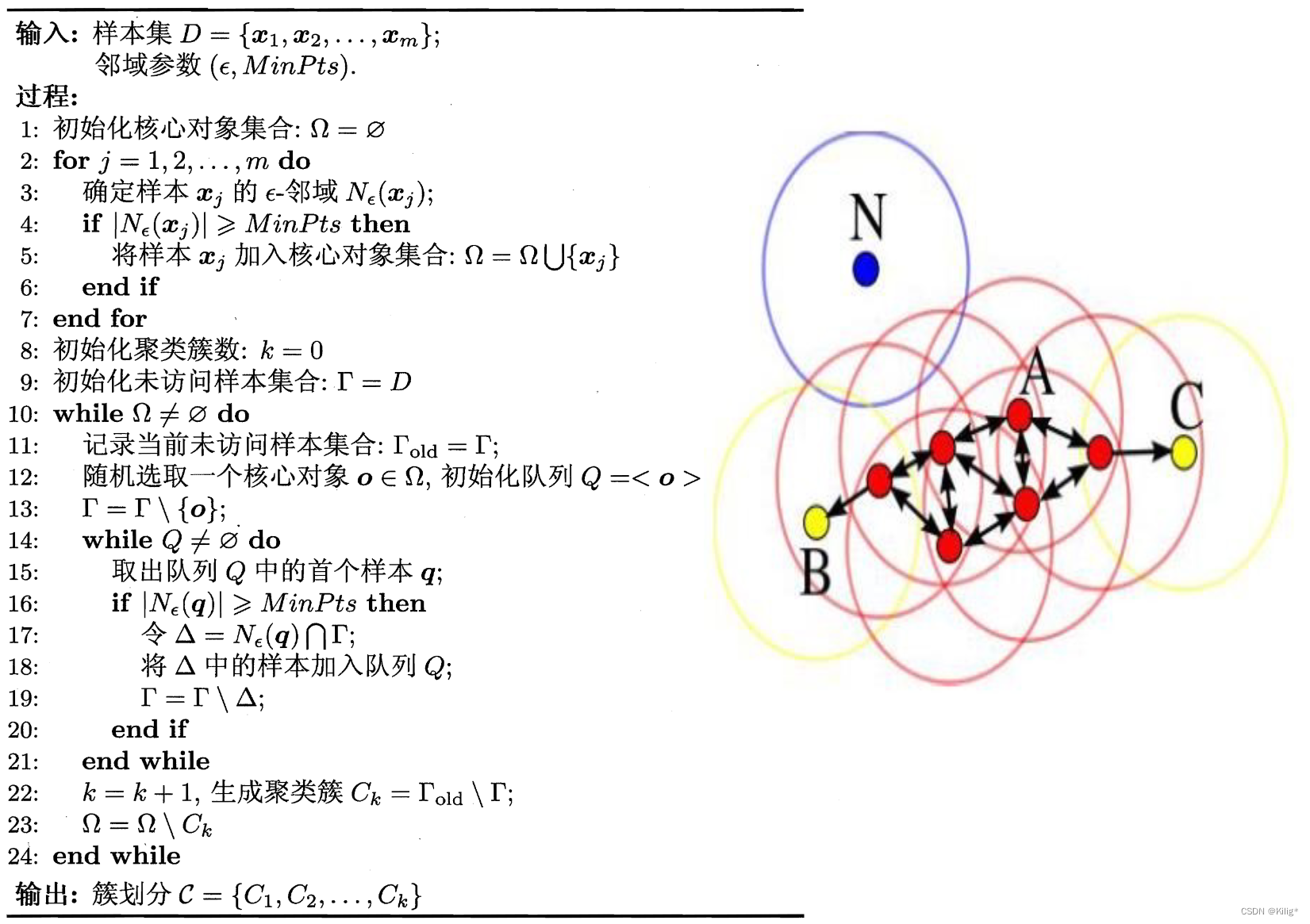
DBSCAN(Density-Based Spatial Clustering of Applications with Noise)是一种基于密度的聚类算法,能够识别具有不同密度的样本点,并能够有效地处理噪声点。DBSCAN通过定义“邻域”和“核心点”来识别簇,并能够发现任意形状的簇结构。
DBSCAN算法步骤:
-
定义邻域:
- 以一个指定的距离阈值 ε \varepsilon ε 作为半径,对每个数据点 p \mathbf{p} p 进行邻域定义。
- 如果在以 p \mathbf{p} p 为中心,半径为 ε \varepsilon ε 的圆球内包含超过指定数量(MinPts)的点,则 p \mathbf{p} p 被视为核心点。
-
寻找核心点和连接簇:
- 根据第一步的定义,寻找所有核心点,并将每个核心点的邻域内的点归为同一个簇。
- 如果点 q \mathbf{q} q 在 p \mathbf{p} p 的邻域内,且 q \mathbf{q} q 也是核心点,则将 q \mathbf{q} q 的簇合并到 p \mathbf{p} p 所在的簇中。
-
处理噪声点:
- 将不能成为核心点,也不在任何核心点的邻域内的数据点视为噪声点或边界点。
DBSCAN的特点:
- 能处理任意形状的簇:相比于K-means等硬聚类算法,DBSCAN能够发现任意形状的簇,对簇的形状没有特定的假设。
- 对噪声点鲁棒:DBSCAN能够识别和过滤噪声点,将其视为离群点。
- 不需要提前指定簇的数量:与K-means等需要提前指定簇数量的算法不同,DBSCAN不需要这个先验信息。
参数说明:
- ε \varepsilon ε:邻域的半径大小。
- MinPts:定义核心点时所需的最小邻域点数。
优势与局限性:
优势:
- 能够识别任意形状的簇结构。
- 对噪声和离群点有较好的鲁棒性。
- 不需要提前指定簇的数量。
局限性:
- 对于密度不均匀的数据或具有差异密度的簇效果可能不理想。
- 对于高维数据集,由于“维度灾难”问题,需要谨慎选择距离阈值和邻域点数。
例题

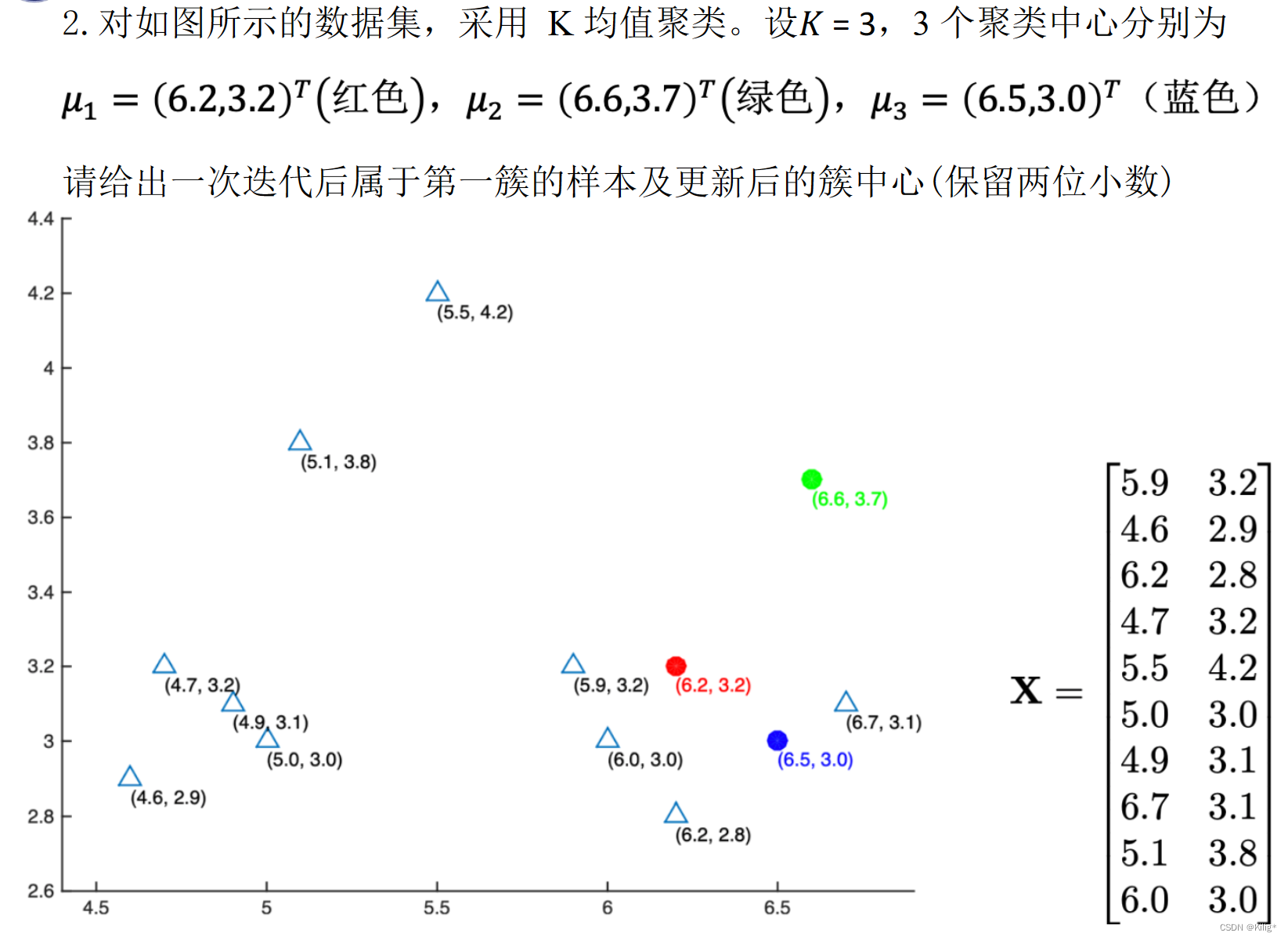
import math
import numpy as np
data=[[5.9, 3.2],
[4.6, 2.9],
[6.2, 2.8],
[4.7, 3.2],
[5.5, 4.2],
[5.0, 3.0],
[4.9, 3.1],
[6.7, 3.1],
[5.1, 3.8],
[6.0, 3.0]]center = [[6.2,3.2],[6.6,3.7],[6.5,3.0]]
def cal_distance(point1, point2):# 计算两点之间的欧氏距离distance = math.sqrt((point1[0] - point2[0])**2 + (point1[1] - point2[1])**2)return distance
def get_min_index(lst):# 获取最小值min_value = min(lst)# 获取最小值的下标min_index = lst.index(min_value)return min_indexdata_dict = {0:[],1:[],2:[]}for i in data:tmp = []print("点:",i,end = '\t')for j in center:tmp.append(round(cal_distance(i,j),2))print(f"距离类别{center.index(j)}的距离:",round(cal_distance(i,j),2),end = '\t')data_dict[get_min_index(tmp)].append(i)print("分配给类别:",get_min_index(tmp))for i in data_dict.keys():print(f"类别{i}的中心为:{np.array(data_dict[i]).mean(axis = 0)}")
输出:
点: [5.9, 3.2] 距离类别0的距离: 0.3 距离类别1的距离: 0.86 距离类别2的距离: 0.63 分配给类别: 0
点: [4.6, 2.9] 距离类别0的距离: 1.63 距离类别1的距离: 2.15 距离类别2的距离: 1.9 分配给类别: 0
点: [6.2, 2.8] 距离类别0的距离: 0.4 距离类别1的距离: 0.98 距离类别2的距离: 0.36 分配给类别: 2
点: [4.7, 3.2] 距离类别0的距离: 1.5 距离类别1的距离: 1.96 距离类别2的距离: 1.81 分配给类别: 0
点: [5.5, 4.2] 距离类别0的距离: 1.22 距离类别1的距离: 1.21 距离类别2的距离: 1.56 分配给类别: 1
点: [5.0, 3.0] 距离类别0的距离: 1.22 距离类别1的距离: 1.75 距离类别2的距离: 1.5 分配给类别: 0
点: [4.9, 3.1] 距离类别0的距离: 1.3 距离类别1的距离: 1.8 距离类别2的距离: 1.6 分配给类别: 0
点: [6.7, 3.1] 距离类别0的距离: 0.51 距离类别1的距离: 0.61 距离类别2的距离: 0.22 分配给类别: 2
点: [5.1, 3.8] 距离类别0的距离: 1.25 距离类别1的距离: 1.5 距离类别2的距离: 1.61 分配给类别: 0
点: [6.0, 3.0] 距离类别0的距离: 0.28 距离类别1的距离: 0.92 距离类别2的距离: 0.5 分配给类别: 0
类别0的中心为:[5.17142857 3.17142857]
类别1的中心为:[5.5 4.2]
类别2的中心为:[6.45 2.95]
相关文章:

模式识别与机器学习-无监督学习-聚类
无监督学习-聚类 监督学习&无监督学习K-meansK-means聚类的优点:K-means的局限性:解决方案: 高斯混合模型(Gaussian Mixture Models,GMM)多维高斯分布的概率密度函数:高斯混合模型ÿ…...

Python中property特性属性是什么
在Java中,通常在类中定义的成员变量为私有变量,在类的实例中不能直接通过对象.属性直接操作,而是要通过getter和setter来操作私有变量。 而在Python中,因为有property这个概念,所以不需要写getter和setter一堆重复的代…...
vue3 全局配置Axios实例
目录 前言 配置Axios实例 页面使用 总结 前言 Axios 是一个基于 Promise 的 HTTP 客户端,用于浏览器和 Node.js 环境。它提供了一种简单、一致的 API 来处理HTTP请求,支持请求和响应的拦截、转换、取消请求等功能。关于它的作用: 发起 HTTP …...

EI级 | Matlab实现TCN-BiGRU-Multihead-Attention多头注意力机制多变量时间序列预测
EI级 | Matlab实现TCN-BiGRU-Multihead-Attention多头注意力机制多变量时间序列预测 目录 EI级 | Matlab实现TCN-BiGRU-Multihead-Attention多头注意力机制多变量时间序列预测预测效果基本介绍模型描述程序设计参考资料 预测效果 基本介绍 1.【EI级】 Matlab实现TCN-BiGRU-Mult…...

WeNet语音识别分词制作词云图
在线体验 ,点击识别语音需要等待一会,文件太大缓存会报错 介绍 本篇博客将介绍如何使用 Streamlit、jieba、wenet 和其他 Python 库,结合语音识别(WeNet)和词云生成,构建一个功能丰富的应用程序。我们将深入了解代码…...
Proxyman:现代本地Web调试代理工具
1. 简介 1.1 什么是Proxyman? Proxyman是一款专为macOS设计的现代本地Web调试代理工具,它不仅支持macOS平台,还能无缝地与iOS和Android设备进行集成。作为一个网络调试工具,Proxyman的设计旨在提供高性能、直观且功能丰富的解决…...

k8s中DaemonSet实战详解
一、DaemonSet介绍 DaemonSet 的主要作用,是在 Kubernetes 集群里,运行一个 Daemon Pod。DaemonSet 只管理 Pod 对象,然后通过 nodeAffinity 和 Toleration 这两个调度器参数的功能,保证了每个节点上有且只有一个 Pod。 二、Daem…...

信号处理设计模式
问题 如何编写信号安全的应用程序? Linux 应用程序安全性讨论 场景一:不需要处理信号 应用程序实现单一功能,不需要关注信号 如:数据处理程序,文件加密程序,科学计算程序 场景二:需要处理信…...
Linux权限的基本理解
一:🚩Linux中的用户 1.1🥦用户的分类 🌟在Linux中用户可以被分为两种用户: 超级用户(root):可以在Linux系统中做各种事情而不被约束普通用户:只能做有限的事情被权限约束 在实际操作时超级用户的命令提示符为#,普通用户的命令提示符为$,可…...

AI人工智能大模型讲师叶梓《基于人工智能的内容生成(AIGC)理论与实践》培训提纲
【课程简介】 本课程介绍了chatGPT相关模型的具体案例实践,通过实操更好的掌握chatGPT的概念与应用场景,可以作为chatGPT领域学习者的入门到进阶级课程。 【课程时长】 1天(6小时/天) 【课程对象】 理工科本科及以上࿰…...

nat地址转换
原理 将内网地址转换成外网地址 方式 掌握动态NAT的配置方法 掌握Easy IP的配置方法 掌握NAT Server的配置方法 实验 r1 r2 是内网 ar1 ip地址 ip add ip地址 掩码 ip route-static 0.0.0.0 0 192.168.1.254 默认网关 吓一跳网关 相等于设置了网关 ar2 …...

第12课 循环综合举例
文章目录 前言一、循环综合举例1. 质数判断问题2. 百人百砖问题3. 猴子吃桃问题4. 质因数分解问题5. 数字统计问题。 二、课后练习2. 末尾3位数问题3. 求自然常数e4. 数据统计问题5. 买苹果问题。6. 找5的倍数问题。 总结 前言 本课使用循环结构,介绍了以下问题的解…...
Tuxera NTFS for Mac2024免费Mac读写软件下载教程
在日常生活中,我们使用Mac时经常会遇到外部设备不能正常使用的情况,如:U盘、硬盘、软盘等等一系列存储设备,而这些设备的格式大多为NTFS,Mac系统对NTFS格式分区存在一定的兼容性问题,不能正常读写。 那么什…...

C++ 具名要求
此页面中列出的具名要求,是 C 标准的规范性文本中使用的具名要求,用于定义标准库的期待。 某些具名要求在 C20 中正在以概念语言特性进行形式化。在那之前,确保以满足这些要求的模板实参实例化标准库模板是程序员的重担。若不这么做…...

大创项目推荐 深度学习二维码识别
文章目录 0 前言2 二维码基础概念2.1 二维码介绍2.2 QRCode2.3 QRCode 特点 3 机器视觉二维码识别技术3.1 二维码的识别流程3.2 二维码定位3.3 常用的扫描方法 4 深度学习二维码识别4.1 部分关键代码 5 测试结果6 最后 0 前言 🔥 优质竞赛项目系列,今天…...
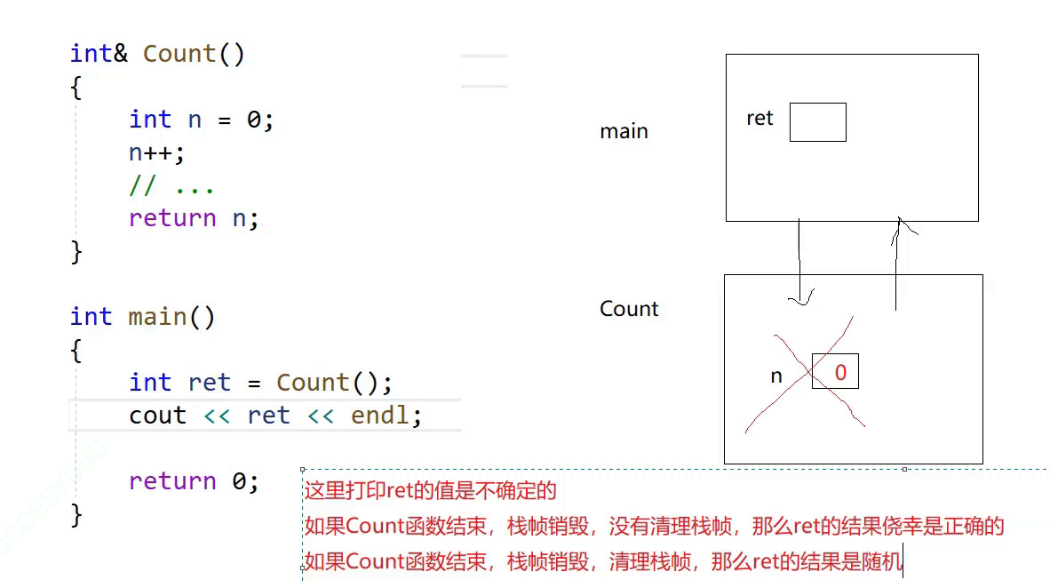
C++初阶——基础知识(函数重载与引用)
目录 1.命名冲突 2.命名空间 3.缺省参数 4.函数重载 1.函数重载的特点包括: 2.函数重载的好处包括: 3.引用 引用的特点包括 引用的主要用途包括 引用和指针 引用 指针 类域 命名空间域 局部域 全局域 第一个关键字 命名冲突 同一个项目之间冲…...
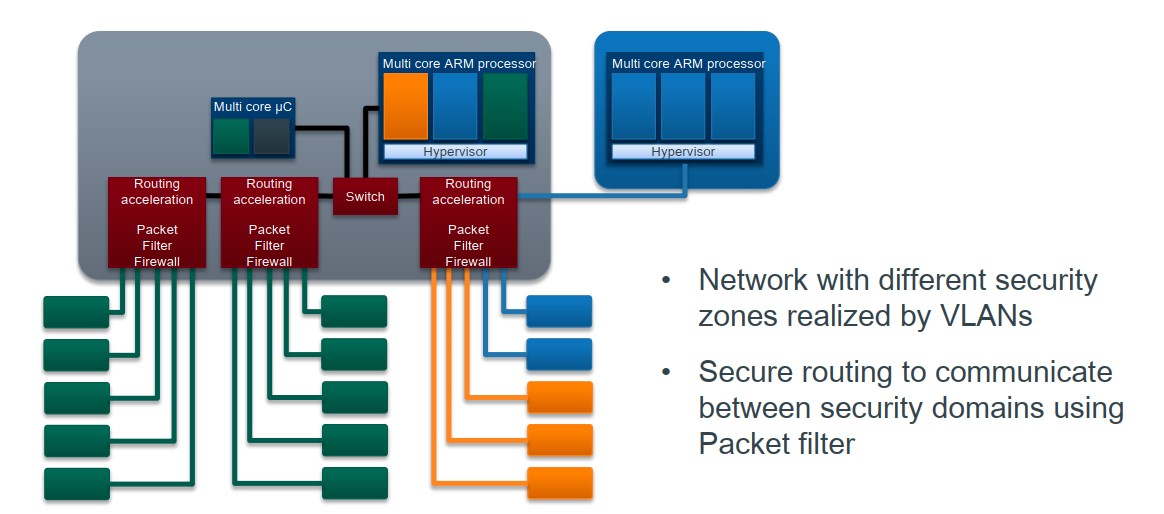
车载电子电器架构 —— 电子电气系统开发角色定义
车载电子电器架构 —— 电子电气系统开发角色定义 我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 注:本文12000字,深度思考者进!!! 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 屏蔽力是信息过载时代一个人的特殊竞争力,任何消耗你的…...
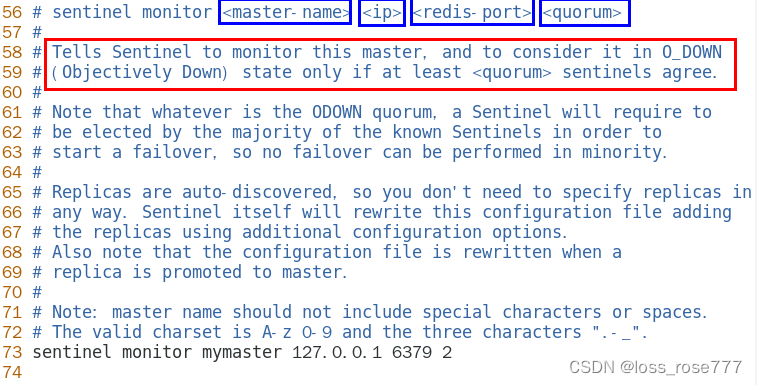
最新Redis7哨兵模式(保姆级教学)
一定一定要把云服务器的防火墙打开一定要!!!!!!!!!否则不成功!!!!!!!!&…...
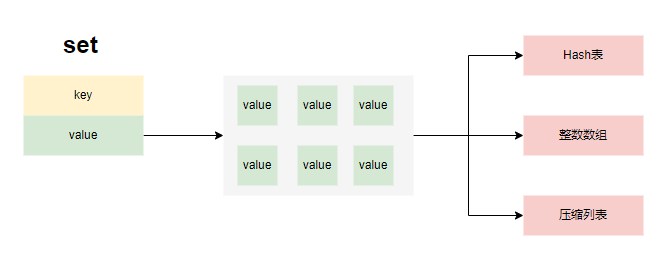
Redis原理及常见问题
高性能之道 单线程模型基于内存操作epoll多路复用模型高效的数据存储结构redis的单线程指的是数据处理使用的单线程,实际上它主要包含 IO线程:处理网络消息收发主线程:处理数据读写操作,包括事务、Lua脚本等持久化线程:执行RDB或AOF时,使用持久化线程处理,避免主线程的阻…...

nvm 的安装及使用 (Node版本管理器)
目录 1、nvm 介绍 2、nvm安装 3、nvm 使用 4、node官网可以查看node和npm对应版本 5、nvm安装指定版本node 6、安装cli脚手架 1、nvm 介绍 NVM 全称 node.js version management ,专门针对 node 版本进行管理的工具,通过它可以安装和切换不同版本的…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

java高级——高阶函数、如何定义一个函数式接口类似stream流的filter
java高级——高阶函数、stream流 前情提要文章介绍一、函数伊始1.1 合格的函数1.2 有形的函数2. 函数对象2.1 函数对象——行为参数化2.2 函数对象——延迟执行 二、 函数编程语法1. 函数对象表现形式1.1 Lambda表达式1.2 方法引用(Math::max) 2 函数接口…...

flow_controllers
关键点: 流控制器类型: 同步(Sync):发布操作会阻塞,直到数据被确认发送。异步(Async):发布操作非阻塞,数据发送由后台线程处理。纯同步(PureSync…...
