<蓝桥杯软件赛>零基础备赛20周--第11周--贪心
报名明年4月蓝桥杯软件赛的同学们,如果你是大一零基础,目前懵懂中,不知该怎么办,可以看看本博客系列:备赛20周合集
20周的完整安排请点击:20周计划
每周发1个博客,共20周。
在QQ群上答疑:

文章目录
- 1. 贪心思想
- 2. 经典贪心问题
- 2.1 部分背包问题
- 2.2 不相交区间问题(或称为区间调度问题、活动安排问题)
- 2.3 区间合并问题
- 2.4 区间覆盖问题
- 3. 例题
- 3.1 买二赠一
- 3.2 购物
- 3.3 管道
- 4. 习题
第9周: 贪心
备赛20周活动已经到第11周了,快到期末考试阶段了。最近做题的人很少了。
1. 贪心思想
贪心是蓝桥杯省赛的必考知识点,每年都有。
贪心(Greedy)是容易理解的算法思想:把整个问题分解成多个步骤,在每个步骤,都选取当前步骤的最优方案,直到所有步骤结束;在每一步,都不考虑对后续步骤的影响,在后续步骤中也不能回头改变前面的选择
作者拟过2句赠言:“贪心说,我从不后悔我走过的路”“贪心说,其实我有一点后悔,但是我回不了头”
大多数读者选前一句。
贪心策略在生活中经常用到。例如下象棋时,初级水平的棋手只会“走一步看一步”,就是贪心法。而水平高的棋手能“走一步看三步”,轻松击败初级棋手。
贪心这种“只顾当下,不管未来”的解题策略,让人疑惑:在完成所有局部最优操作后,得到的解不一定是全局最优,那么热如何判断能不能用贪心呢?
有时很容易判断:一步一步在局部选择最优,最后结束时能达到全局最优。例如吃自助餐,怎么吃才能“吃回票价”?它的数学模型是一类背包问题,称为“部分背包问题”:有一个容量为C的背包,有m种物品,第i种物品有wi千克,单价为vi,且每种物品是可以分割的,例如大米、面粉等;问如何选择物品,使得装满背包时,总价值最大。显然可以用贪心法,只要在当前物品中选最贵的放进背包就行了:先选最贵的物品A,A放完之后,再选剩下最贵的物品B,…,直到背包放满。
有时看起来能用贪心,但实际上贪心的结果不是最优解。例如最少硬币支付问题:有多种面值的硬币,数量不限;需要支付M元,问怎么支付,才能使硬币数量最少?
最少硬币支付问题是否能用贪心求最优解,和硬币的面值有关。
任意面值的最少硬币支付问题,正解是动态规划。参考《算法竞赛入门到进阶》清华大学出版社,罗勇军著,“7.1.1 硬币问题”给出了各种硬币问题的动态规划解法。
如果硬币面值为1元、2元、5元,用贪心是对的。贪心策略是当前选择可用的最大面值的硬币。例如支付M=18元,第一步选面值最大的5元硬币,用掉3个硬币,还剩3元;第二步选面值第二大的2元硬币,用掉1个硬币,还剩1元;最后选面值最小的1元硬币,用掉1个;共用5个硬币。在这个解决方案中,硬币数量总数是最少的,贪心法的结果是全局最优的。
但是如果是其他面值的硬币,贪心法就不一定能得到全局最优解。例如,硬币的面值很奇怪,分别是1、2、4、5、6元。支付M = 9元,如果用贪心法,每次选择当前最大面值硬币,那么答案是6 + 2 + 1,需要3个硬币,而最优解是5 + 4,只需要2个硬币。
判断一个题目是不是能用贪心,需要满足以下特征:
1)最优子结构性质。当一个问题的最优解包含其子问题的最优解时,称此问题具有最优子结构性质,也称此问题满足最优性原理。
2)贪心选择性质。问题的整体最优解可以通过一系列局部最优的选择来得到。也就是说,通过一步步局部最优能最终能得到全局最优。
最后讨论贪心法的效率,贪心法的计算量是多少?贪心法由于每一步都在局部做计算,且只选取当前最优的步骤做计算,不管其他可能的计算方案,所以计算量很小。在很多情况下,贪心法可以说是计算复杂度最低的算法了。与此相对,暴力法一般是计算复杂度最差的,因为暴力法计算了全局的所有可能的方案。
由于贪心的效率高,所以如果一个问题确定可用贪心法能得到最优解,那么应该使用贪心。如果用其他算法,大概率会超时。
在算法竞赛中,贪心法几乎是必考点,有的题考验思维能力,有的题结合了贪心和其他算法。虽然贪心策略很容易理解,但贪心题可能很难。
贪心也是蓝桥杯大赛的常见题型。不论是省赛还是国赛,贪心出现的概率都非常大。
虽然贪心法不一定能得到最优解,但是它解题步骤简单、编程容易、计算量小,得到的解“虽然不是最好,但是还不错!”。像蓝桥杯这种赛制,一道题有多个测试点,用贪心也许能通过10%~30%,若别无他法,值得一试。
2. 经典贪心问题
2.1 部分背包问题
前文介绍了用贪心求解部分背包问题,下面是例题。
例题:部分背包问题
下面直接给出代码。
C++代码
#include<bits/stdc++.h>
using namespace std;
struct gold{ double w,v,p; }a[105]; //w,v,p: 重量,价值,单价
bool cmp(gold a, gold b){ return a.p > b.p; } //单价从大到小排序
int main(){int n,c; cin>>n>>c;for(int i=0;i<n;i++){cin >> a[i].w >> a[i].v;a[i].p = a[i].v/a[i].w; //计算单价}sort(a,a+n,cmp); //按单价排序double sum=0.0; //最大价值for(int i=0;i<n;i++){if(c >= a[i].w){ //第i种金币比背包容量小c -= a[i].w; //背包还有余量sum += a[i].v; //累计价值}else{ //第i种金币很多,直接放满背包sum += c*a[i].p;break;}}printf("%.2f",sum);//保留小数点后两位输出return 0;
}
Java代码
import java.util.*;
class Main {static class Gold { double w, v, p; }public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int c = scanner.nextInt();Gold[] a = new Gold[n];for (int i = 0; i < n; i++) {a[i] = new Gold();a[i].w = scanner.nextDouble();a[i].v = scanner.nextDouble();a[i].p = a[i].v/a[i].w;}Arrays.sort(a, new Comparator<Gold>() {public int compare(Gold a, Gold b) {return Double.compare(b.p, a.p);}});double sum = 0.0;for (int i = 0; i < n; i++) {if (c >= a[i].w) {c -= a[i].w;sum += a[i].v;} else {sum += c * a[i].p;break;}}System.out.printf("%.2f", sum);}
}
Python代码
n, c = map(int, input().split())
a = []
for i in range(n):w, v = map(int, input().split())p = v / wa.append((w, v, p))
a.sort(key=lambda x: x[2], reverse=True)
sum = 0.0
for i in range(n):if c >= a[i][0]:c -= a[i][0]sum += a[i][1]else:sum += c * a[i][2]break
print("%.2f" %sum)
2.2 不相交区间问题(或称为区间调度问题、活动安排问题)
给定一些区间(活动),每个区间有左端点和右端点(开始时间和终止时间),要求找到最多的不相交区间(活动)。
以下按“活动安排问题”来解释。
这个问题的目的是求最多活动数量,所以那种持续时间长的活动不受欢迎,受欢迎的是尽快结束的、持续时间短的活动。
考虑以下3种贪心策略:
1)按最早开始时间贪心:先选最早开始的活动a,当a结束后,再选下一个最早开始的活动。这种策略不好,因为它没有考虑活动的持续时间。假如a一直不结束,那么其他活动就不能开始。
2)最早结束时间:先选最早结束的活动a,a结束后,再选下一个最早结束的活动。这种策略是合理的。越早结束的活动,越能腾出后续时间容纳更多的活动。
3)用时最少:先选时间最短的活动a,再选不冲突的下一个最短活动。这个策略似乎也可行,但是很容易找到反例,证明这个策略不正确。
下图的例子,
用“策略1)最早开始时间”,选3;
用“策略2)最早结束时间”,选1、2、5、6;
用“策略3)用时最少”,选4、1、2。
策略2)的结果是最好的。
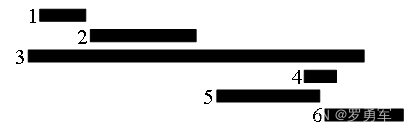
总结活动安排问题的贪心策略:先按活动的结束时间(区间右端点)排序,然后每次选结束最早的活动,并保证选择的活动不重叠。
例题:线段覆盖
C++代码
#include<bits/stdc++.h>
using namespace std;
struct data{int L, R; //开始时间、结束时间
}a[1000005];
bool cmp(data x,data y){return x.R<y.R; } //按照结束时间排序
int main(){int n; cin >> n;for(int i=0;i<n;i++) cin>>a[i].L>>a[i].R;sort(a,a+n,cmp);int ans = 0;int lastend = -1;for(int i=0;i<n;i++)if(a[i].L>=lastend) {ans++;lastend = a[i].R;}cout<<ans;return 0;
}
Java代码
import java.util.*;
class Main {static class Data { int L, R; } // 开始时间、结束时间public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();Data[] a = new Data[n];for (int i = 0; i < n; i++) {a[i] = new Data();a[i].L = scanner.nextInt();a[i].R = scanner.nextInt();}Arrays.sort(a, new Comparator<Data>() {public int compare(Data x, Data y) {return x.R - y.R;}});int ans = 0;int lastend = -1;for (int i = 0; i < n; i++) if (a[i].L >= lastend) {ans++;lastend = a[i].R;}System.out.println(ans);}
}
python代码
n = int(input())
a = []
for _ in range(n):L, R = map(int, input().split())a.append((L, R))
a.sort(key=lambda x: x[1]) # 按照结束时间排序。请与下一个例题比较
ans = 0
lastend = -1
for i in range(n):if a[i][0] >= lastend:ans += 1lastend = a[i][1]
print(ans)
2.3 区间合并问题
区间合并问题:给定若干个区间,合并所有重叠的区间,并返回不重叠的区间个数。
以下图为例,1、2、3、5合并,4、6合并,新区间是1’、4’。

贪心策略:按区间左端点排序,然后逐一枚举每个区间,合并相交的区间。
定义不重叠的区间个数(答案)为ans。设当前正在合并的区间的最右端点为end,枚举到第i个区间[Li, Ri]时:
若Li≤end,说明与第i区间相交,需要合并,ans不变,更新end = max(end, Ri)。
若Li > end,说明与第i区间不相交,ans加1,更新 end = max(end, Ri)。
请读者用上图的例子,模拟合并过程。
2.4 区间覆盖问题
区间覆盖问题:给定一个目标大区间,和一些小区间,问最少选择多少小区间,可以覆盖大区间。
贪心策略:尽量找出右端点更远的小区间。
操作步骤:先对小区间的左端点排序,然后依次枚举每个小区间,在所有能覆盖当前目标区间右端点的区间之中,选择右端点最大的区间。
下图中,求最少用几个小区间能覆盖整个区间。先按左端点排序。设当前覆盖到了位置R,选择的小区间数量为cnt。

从区间1开始,R的值是区间1的右端点A,R=A。cnt=1。
找到能覆盖R=A的区间2、3,在区间2、3中选右端点更远的3,更新R为区间3的右端点B,R=B。cnt=2。
区间4不能覆盖R=B,跳过。
找到能覆盖R=B区间5,更新R=C。cnt=3。结束。
例题:区间覆盖
C++代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
struct data{ll L,R;
} a[100005];
bool cmp(data x,data y){return x.L < y.L; } //按左端点排序
int main(){int n; cin>>n;for (int i=0;i<n;i++) cin>>a[i].L>>a[i].R;sort(a,a+n,cmp);ll lastend=-1,ans=0;for (int i=0;i<n;i++)if (a[i].R >= lastend){ans += a[i].R - max(lastend,a[i].L)+1;lastend = a[i].R+1;}cout<<ans;return 0;
}
Java代码
import java.util.*;class Main {static class Data {long L, R;}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();Data[] a = new Data[n];for (int i = 0; i < n; i++) {a[i] = new Data();a[i].L = scanner.nextLong();a[i].R = scanner.nextLong();}Arrays.sort(a, new Comparator<Data>() {public int compare(Data x, Data y) {return Long.compare(x.L, y.L);}});long lastend = -1;long ans = 0;for (int i = 0; i < n; i++) if (a[i].R >= lastend) {ans += a[i].R - Math.max(lastend, a[i].L) + 1;lastend = a[i].R + 1;}System.out.println(ans);}
}
python代码
class Data: def __init__(self, L, R):self.L = Lself.R = R
def cmp(x, y): return x.L < y.L #这里用函数比较。请对比上一题代码n = int(input())
a = []
for _ in range(n):L, R = map(int, input().split())a.append(Data(L, R))
a.sort(key=lambda x: x.L)
lastend = -1
ans = 0
for i in range(n):if a[i].R >= lastend:ans += a[i].R - max(lastend, a[i].L) + 1lastend = a[i].R + 1
print(ans)3. 例题
3.1 买二赠一
2023年蓝桥杯省赛 Java B组 G题 20分
看起来这20分不难拿哦
链接:买二赠一
最贵的商品显然不能免单,买了2个不能免单的最贵商品后,获得一个免单机会,那么这个免单机会给谁呢?就给能免单的最贵的那个商品。这个贪心思路显然是对的。
以样例为例,先排序得{8 7 5 4 2 1 1}。先购买最贵的8、7,然后可以免单的最贵的是2。再购买剩下的最贵的5、4,免单1。最后单独买1。总价是25。
C++代码。需要查找价格为P/2的商品, 由于价格已经排序,可以用二分法加快查找的时间。这里直接用二分法的库函数lower_bound()查找。
#include<bits/stdc++.h>
using namespace std;
const int N = 5e5 + 10;
int a[N];
bool vis[N]; //vis[i]=1表示已经免单了
int main(){int n; scanf("%d", &n);for(int i = 0; i < n; i++) scanf("%d", &a[i]);sort(a, a + n);long long ans = 0;int cnt = 0;int last = -1; //购买的2件中的便宜的那件last_id = n-1; //能免单的位置for(int i = n-1; i >= 0; i--){if(!vis[i])cnt++, ans += a[i], last = a[i]; //last是买的第2件if(cnt == 2){ //买了2个cnt = 0;int x = lower_bound(a , a + last_id, last / 2) - a; //找能免单的商品a[x]if(x > last_id || a[x] > last / 2) x--; //向下取整if(x>=0){vis[x] = 1; //x免单了last_id = x-1; //后面能免单的区间范围是[0,last_id]}}}cout<<ans<<endl;return 0;
}
Java代码。Java没有自带的二分函数,只好自己写一个lowerBound()。
import java.util.Arrays;
import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int[] a = new int[n];for (int i = 0; i < n; i++) a[i] = scanner.nextInt();Arrays.sort(a);long ans = 0;int cnt = 0;int last = -1;int last_id = n - 1;boolean[] vis = new boolean[n];for (int i = n - 1; i >= 0; i--) {if (!vis[i]) {cnt++;ans += a[i];last = a[i];}if (cnt == 2) {cnt = 0;int x = lowerBound(a, 0, last_id, last / 2);if (x > last_id || a[x] > last / 2) x--;if (x >= 0) {vis[x] = true;last_id = x - 1;}}}System.out.println(ans);}private static int lowerBound(int[] a, int L, int R, int target) {while (L < R) {int mid = L + (R - L) / 2;if (a[mid] >= target) R = mid;else L = mid + 1;}return L;}
}Python代码。自带的二分函数是bisect_left()。
import bisect
n = int(input())
a = list(map(int, input().split()))
a.sort()
ans = 0
cnt = 0
last = -1
last_id = n - 1
vis = [False] * n
for i in range(n - 1, -1, -1):if not vis[i]:cnt += 1ans += a[i]last = a[i]if cnt == 2:cnt = 0x = bisect.bisect_left(a, last // 2, 0, last_id)if x > last_id or a[x] > last // 2: x -= 1if x >= 0:vis[x] = Truelast_id = x - 1
print(ans)
3.2 购物
链接:购物
为方便处理,把硬币面值从小到大排序。
无解是什么情况?如果没有面值1的硬币,组合不到1,无解。如果有面值1的硬币,那么所有的X都能满足,有解。所以,无解的充要条件是没有面值1的硬币。
组合出1~X的任意值,需要的硬币多吗?学过二进制的人都知道,1、2、4、8、…、 2 n − 1 2^{n-1} 2n−1这n个值,可以组合出1~ 2 n 2^n 2n-1的所有数。这说明,只需要很少的硬币,就能组合出很大的X。
设已经组合出1~s的面值,即已经得到数字1、2、3、…、s,下一步扩展到s+1。当然,如果能顺便扩展到s+2、s+3、…扩展得越大越好,这样就能用尽量少的硬币扩展出更大的面值。
如何扩展到s+1?就是在数字1、2、3、…、s的基础上,添加一个面值为v的硬币,得到s+1。v可以选1、2、…、s+1,例如:v=1,s+1=s+v;v=2,s+1=s-1+v;…;v=s+1,s+1=v。如果v=s+2,就不能组合到s+1了。
v的取值范围是[1, s+1],为了最大扩展,选v为[1, s+1]内的最大硬币,此时s扩展到s+v。这就是贪心策略。
以本题的输入样例为例说明计算过程。设答案为ans。
先选硬币1,得到s=1。ans=1。
再选[1, s+1]=[1, 2]内的最大硬币2,扩展s=1为s=1+v=3。ans=2。
再选[1, s+1]=[1, 4]内的最大硬币2,得到s=5。ans=3。
再选[1, s+1]=[1, 6]内的最大硬币5,得到s=10。ans=4。
再选[1, s+1]=[1, 11]内的最大硬币10,得到s=20。ans=5。此时s≥X,结束。
所以仅需5个面值1、2、2、5、10的硬币,就可以组合得到1、2、3、4、…、20。
C/C++代码。第11行找[1, s]内的最大面值硬币,可以用二分法优化。本题不优化也能通过测试。
#include <bits/stdc++.h>
using namespace std;
int a[105]; //存硬币面值
int main(){int x,n; cin >> x >>n;for(int i=0;i<n;i++) cin >> a[i];sort(a,a+n);if(a[0]!=1){ cout<<-1; return 0;} //无解int s=0,ans=0;while(s<x)for(int v=n-1;v>=0;v--)if(a[v]<=s+1) { //找到[1,s]内的最大面值硬币a[v]s+=a[v]; //扩展sans++;break;}cout << ans;
}
Java代码
import java.util.Arrays;
import java.util.Scanner;
public class Main {public static void main(String[] args) {Scanner input = new Scanner(System.in);int x = input.nextInt();int n = input.nextInt();int[] a = new int[n];for (int i = 0; i < n; i++) a[i] = input.nextInt(); Arrays.sort(a);if (a[0] != 1) { System.out.println(-1); return; }int s = 0;int ans = 0;while (s < x) for (int v = n - 1; v >= 0; v--) if (a[v] <= s + 1) {s += a[v];ans++;break;}System.out.println(ans);}
}
python代码
x, n = map(int, input().split())
a = list(map(int, input().split()))
a.sort()
if a[0] != 1: print(-1); exit()
s, ans = 0, 0
while s < x:for v in range(n - 1, -1, -1):if a[v] <= s + 1:s += a[v]ans += 1break
print(ans)3.3 管道
2023年蓝桥杯省赛 Python B组 D题 10分
这10分似乎不难拿
链接:管道
按题目的设定,管道内是贯通的,每个阀门都连着一个进水管,打开阀门后会有水从这个进水管进入管道,并逐渐流到管道内所有地方。
先解释样例。设长度L的单位是米,水流的速度是米/秒。
L=1处的阀门在第S=1秒打开,T=5秒时,覆盖范围L-(T-S)=1-(5-1)=-3,L+(T-S)=1+(5-1)=5;
L=6处的阀门在S=5秒打开,T=5秒时,只覆盖了L=6;
L=10处的阀门在L=2秒打开,T=5秒时,覆盖范围L-(T-S)=10-(5-2)=7,L+(T-S)=10+(5-2)=13。
所以这3个阀门在T=5时,覆盖了[-3, 5]、6、[7,13],管道所有传感器都检测到了水流。
读者可能立刻想到可以用二分法猜时间T。先猜一个T,然后判断在T时刻是否整个管道有水。如何判断?位于Li的阀门,它影响到的小区间是[Li-(Ti-Si), Li+(Ti-Si)],n个阀门对应了n个小区间。那么问题转化为:给出n个小区间,是否能覆盖整个大区间,这就是上一节提到的“区间覆盖问题”。
本题还可以再简单一点。题目给的评测用例指出Li-1 < Li,即已经按左端点排序了,可以省去排序的步骤。
C++代码。在check((t)函数中,定义last_L为当前覆盖到的最左端,last_R为最右端。然后逐个遍历所有的小区间,看它对扩展last_L、last_R有无贡献。所有小区间处理完毕后,如果[last_L、last_R]能覆盖整个[1, len]区间,这个时刻t就是可行的。
第32行把二分mid写成mid = ((R - L) >> 1) + L而不是mid = (R + L) >> 1,是因为R+L可能溢出。R的最大值是2e9,L的最大值是1e9,R+L超过了int的范围。为什么第30行定义R的初值为2e9?请读者思考。
C++代码
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
const int LEN = 1e9;
int n, len;
int L[N], S[N];
bool check(int t){ // 检查t时刻,管道内是否都有水int cnt = 0;int last_L = 2, last_R = 1;for(int i = 0; i < n; i++)if(t >= S[i]){cnt++; //特判t是否够大int left = L[i] - (t - S[i]);int right = L[i] + (t - S[i]);if(left < last_L)last_L = left, last_R = max(last_R, right);else if(left <= last_R + 1)last_R = max(last_R, right);}if(cnt == 0) return false;if(last_L <= 1 && last_R >= len)return true;elsereturn false;
}
int main(){scanf("%d%d", &n, &len);for(int i = 0; i < n; i++)scanf("%d%d", &L[i], &S[i]);int L = 0, R = 2e9, ans = -1;while(L <= R){ //二分int mid = ((R - L) >> 1) + L; //如果写成(L+R)>>1可能溢出if(check(mid)) ans = mid, R = mid - 1;else L = mid + 1;}printf("%d\n", ans);return 0;
}
Java代码
import java.util.Scanner;
public class Main {static int[] L;static int[] S;static int n;static int len;public static boolean check(int t) {int cnt = 0;int last_L = 2;int last_R = 1;for(int i = 0; i < n; i++) {if(t >= S[i]) {cnt++;int left = L[i] - (t - S[i]);int right = L[i] + (t - S[i]);if(left < last_L) {last_L = left;last_R = Math.max(last_R, right);} else if(left <= last_R + 1) {last_R = Math.max(last_R, right);}}}if(cnt == 0) return false;if(last_L <= 1 && last_R >= len) return true;else return false;}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);n = scanner.nextInt();len = scanner.nextInt();L = new int[n];S = new int[n];for(int i = 0; i < n; i++) {L[i] = scanner.nextInt();S[i] = scanner.nextInt();}int L = 0;int R = 2000000000;int ans = -1;while(L <= R) {int mid = ((R - L) >> 1) + L;if(check(mid)) {ans = mid;R = mid - 1;} else L = mid + 1; }System.out.println(ans);}
}
python代码
def check(t):cnt = 0last_L = 2last_R = 1for i in range(n):if t >= S[i]:cnt += 1left = L[i] - (t - S[i])right = L[i] + (t - S[i])if left < last_L:last_L = leftlast_R = max(last_R, right)elif left <= last_R + 1:last_R = max(last_R, right)if cnt == 0: return Falseif last_L <= 1 and last_R >= length: return Trueelse: return Falsen, length = map(int, input().split())
L = []
S = []
for _ in range(n):l, s = map(int, input().split())L.append(l)S.append(s)
L_val,R_val =0, int(2e9)
ans = -1
while L_val <= R_val:mid = (R_val + L_val) >> 1if check(mid):ans = midR_val = mid - 1else: L_val = mid + 1
print(ans)4. 习题
答疑 https://www.lanqiao.cn/problems/1025/learning/
身份证 https://www.lanqiao.cn/problems/3849/learning/
翻硬币 https://www.lanqiao.cn/problems/209/learning/
防御力 https://www.lanqiao.cn/problems/226/learning/
合并果子 https://www.luogu.com.cn/problem/P1090
排队接水 https://www.luogu.com.cn/problem/P1223
小A的糖果 https://www.luogu.com.cn/problem/P3817
负载平衡问题 https://www.luogu.com.cn/problem/P4016
找零钱 https://www.lanqiao.cn/problems/3854
01搬砖 https://www.lanqiao.cn/problems/2201/learning/
卡牌游戏 https://www.lanqiao.cn/problems/1057/learning
寻找和谐音符 https://www.lanqiao.cn/problems/3975/learning
三国游戏 https://www.lanqiao.cn/problems/3518/learning/
平均 https://www.lanqiao.cn/problems/3532/learning/
小蓝的旅行计划 https://www.lanqiao.cn/problems/3534/learning/
排座椅 https://www.luogu.com.cn/problem/P1056
母舰 https://www.luogu.com.cn/problem/P2813
加工生产调度 https://www.luogu.com.cn/problem/P1248
相关文章:

<蓝桥杯软件赛>零基础备赛20周--第11周--贪心
报名明年4月蓝桥杯软件赛的同学们,如果你是大一零基础,目前懵懂中,不知该怎么办,可以看看本博客系列:备赛20周合集 20周的完整安排请点击:20周计划 每周发1个博客,共20周。 在QQ群上答疑&#x…...

PowerShell Instal 一键部署TeamCity
前言 TeamCity 是一个通用的 CI/CD 软件平台,可实现灵活的工作流程、协作和开发实践。允许在您的 DevOps 流程中成功实现持续集成、持续交付和持续部署。 系统支持 Centos7,8,9/Redhat7,8,9及复刻系列系统支持 Windows 10,11,2012,2016,2019,2022高版本建议使用9系列系统…...
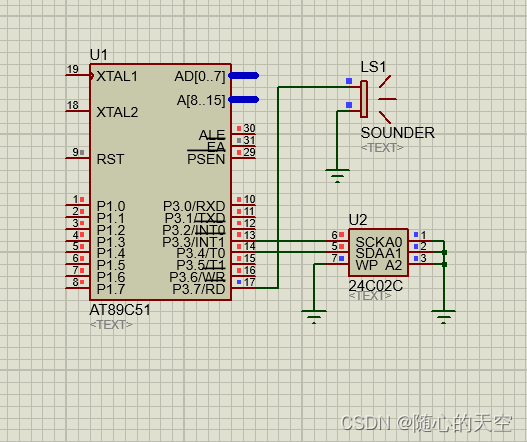
将“渴望“乐谱写入AT24C02并读出播放
#include <reg51.h> // 包含51单片机寄存器定义的头文件 #include <intrins.h> //包含_nop_()函数定义的头文件 #define OP_READ 0xa1 // 器件地址以及读取操作,0xa1即为1010 0001B #define OP_WRITE 0xa0 // 器件地址以及写…...
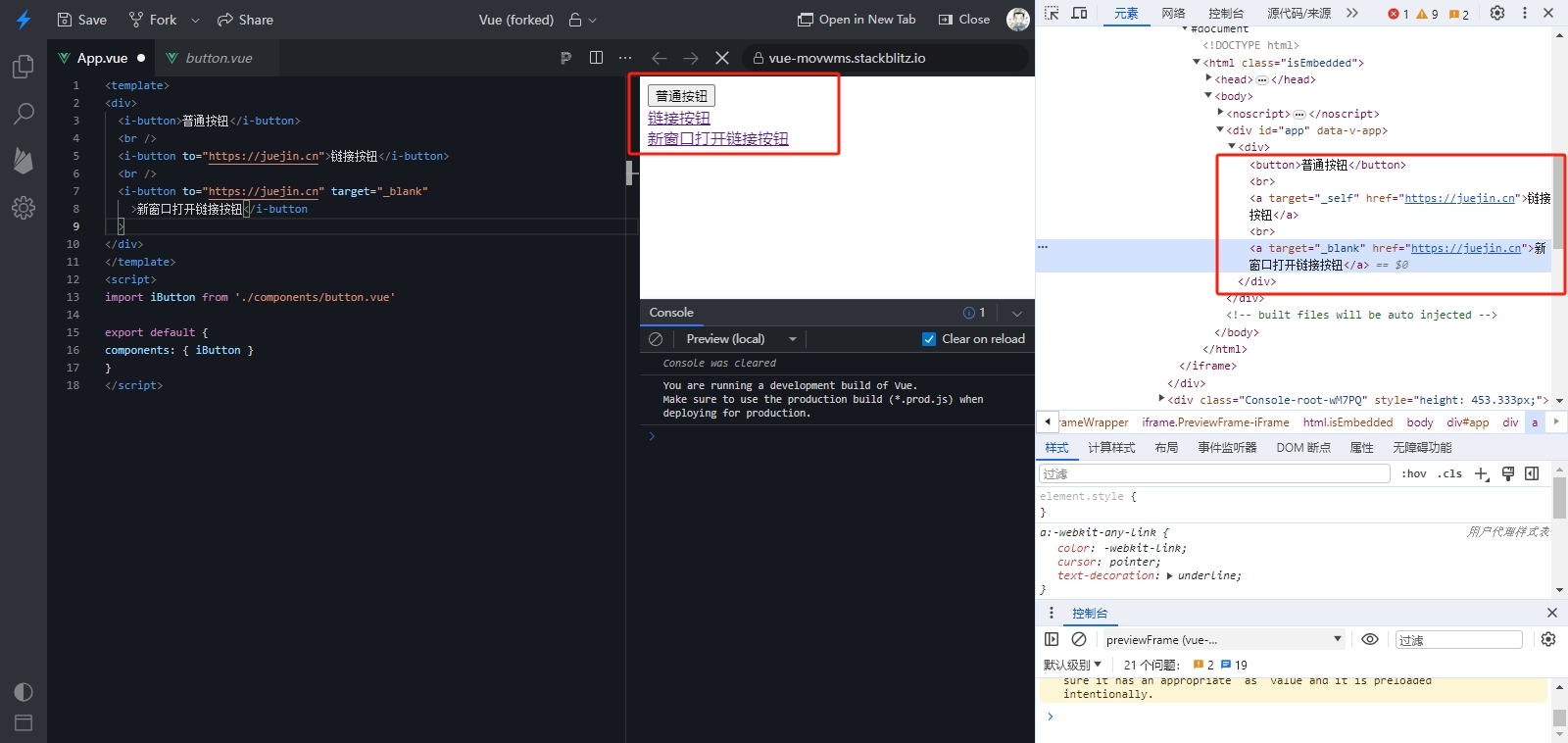
Vue独立组件开发-动态组件
文章目录 一、前言二、实现三、优化四、总结五、最后 一、前言 在开发中,你经常会遇到这么一种情况:根据条件动态地切换某个组件,或动态地选择渲染某个组件。 Vue 提供了另外一个内置的组件 <component> 和 is 特性,可以更…...
)
前端八股文(HTML篇)
目录 1.什么是DOCTYPE,有何用呢? 2.说说对html语义化的理解 3.src和href的区别? 4.title与h1的区别,b与strong的区别,i与em的区别? 5.什么是严格模式与混杂模式? 6.前端页面有哪三层构成,分…...

RivaGAN 水印项目
git地址 https://github.com/DAI-Lab/RivaGAN Dockerfile (/tools下文件为git下的文件) ############################################### # 使用 NVIDIA CUDA 10.0 开发环境作为基础镜像 FROM kaldiasr/kaldi:gpu-ubuntu18.04-cuda10.0 # 设置非交互式安装模式以避免某些命…...

Games101作业5
1.实现Renderer.cpp 中的 Render():为每个像素生成光线 这里你需要为每个像素生成一条对应的光 线,然后调用函数 castRay() 来得到颜色,最后将颜色存储在帧缓冲区的相 应像素中。 我们要做的就是将屏幕空间下的坐标最后转换到世界空间的坐标…...

Golang解决跨域问题【OPTIONS预处理请求】
Golang解决跨域问题 前置知识:跨域问题产生条件及原因 跨域是是因为浏览器的同源策略限制,是浏览器的一种安全机制,服务端之间是不存在跨域的。 所谓同源指的是两个页面具有相同的协议、主机和端口,三者有任一不相同即会产生跨域…...
算法篇)
复试 || 就业day05(2023.12.31)算法篇
文章目录 前言找不同最长回文串找到所有数组中消失的数字下一个更大元素 I键盘行 前言 💫你好,我是辰chen,本文旨在准备考研复试或就业 💫文章题目大多来自于 leetcode,当然也可能来自洛谷或其他刷题平台 💫…...
Spring-4-代理
前面提到过,在Spring中有两种类型的代理:使用JDK Proxy类创建的JDK代理以及使用CGLIB Enhancer类创建的基于CGLIB的代理。 你可能想知道这两种代理之间有什么区别,以及为什么 Spring需要两种代理类型。 在本节中,将详细研究代理…...

设计模式:抽象工厂模式(讲故事易懂)
抽象工厂模式 定义:将有关联关系的系列产品放到一个工厂里,通过该工厂生产一系列产品。 设计模式有三大分类:创建型模式、结构型模式、行为型模式 抽象工厂模式属于创建型模式 上篇 工厂方法模式 提到工厂方法模式中每个工厂只生产一种特定…...

C语言中的Strict Aliasing Rule
文章目录 前言没有警告不代表没有问题目前的应对方法 前言 很久没写了,水一篇。 最近有个代码在gcc 4.8.5上编译失败。编译失败的提示是: error: dereferencing type-punned pointer will break strict-aliasing rules [-Werrorstrict-aliasing]查了下…...
单字符检测模型charnet使用方法,极简
Git链接 安装按照上面的说明,说下使用。 把tools下面的test做了一点修改,可以读取一张图片,把里面的单个字符都检测和识别出来。 然后绘制到屏幕上。 import torch from charnet.modeling.model import CharNet import cv2, os import num…...

Erlang、RabbitMQ下载与安装教程(windows超详细)
目录 安装Erlang 1.首先安装RabbitMQ需要安装Erlang环境 2.点击下载好的.exe文件进行傻瓜式安装,一直next即可 3.配置Erlang环境变量 安装RabbitMQ 1.给出RabbitMQ官网下载址:Installing on Windows — RabbitMQ,找到 2.配置RabbitMQ环境变量࿰…...

2023年终总结丨很苦,很酷!
文章目录 个人简介丨了解博主写在前面丨博主介绍年终总结丨博主成就年终总结丨博主想说年终总结丨学习芝士年终总结丨未来展望写在后面丨新年快乐 个人简介丨了解博主 主页地址:https://blog.csdn.net/m0_68111267 荣誉身份 ⭐2022年度CSDN 社区之星 Top6 ⭐2023年…...
鸿蒙 DevEco Studio 3.1 入门指南
本文主要记录开发者入门,从软件安装到项目运行,以及后续的学习 1,配置开发环境 1.1 下载安装包 官网下载链接 点击立即下载找到对应版版本 下载完成,按照提示默认安装即可 1.2 下载SDK及工具链 运行已安装的DevEco Studio&…...
ubuntu多用户环境dockerbug,卸载重装docker流程
之前不小心误操作删除重装docker,结果删除没成功,更没法重装,每次apt install都会报一个docker错误,虽然不影响软件的常规安装~但是现在还是需要装一个完整docker,还是选择删除一下,重点是关闭服…...
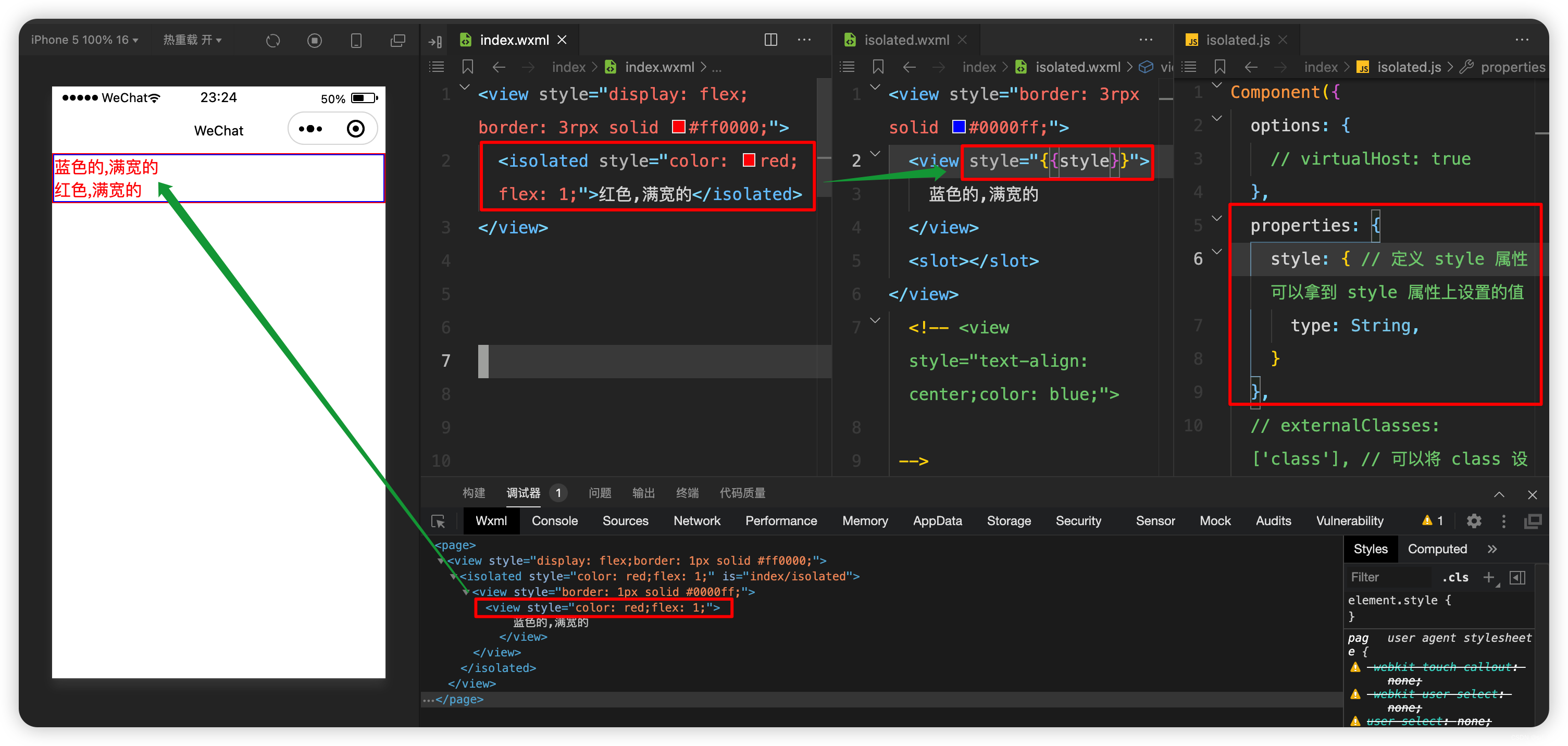
微信小程序开发系列-09自定义组件样式特性
微信小程序开发系列目录 《微信小程序开发系列-01创建一个最小的小程序项目》《微信小程序开发系列-02注册小程序》《微信小程序开发系列-03全局配置中的“window”和“tabBar”》《微信小程序开发系列-04获取用户图像和昵称》《微信小程序开发系列-05登录小程序》《微信小程序…...
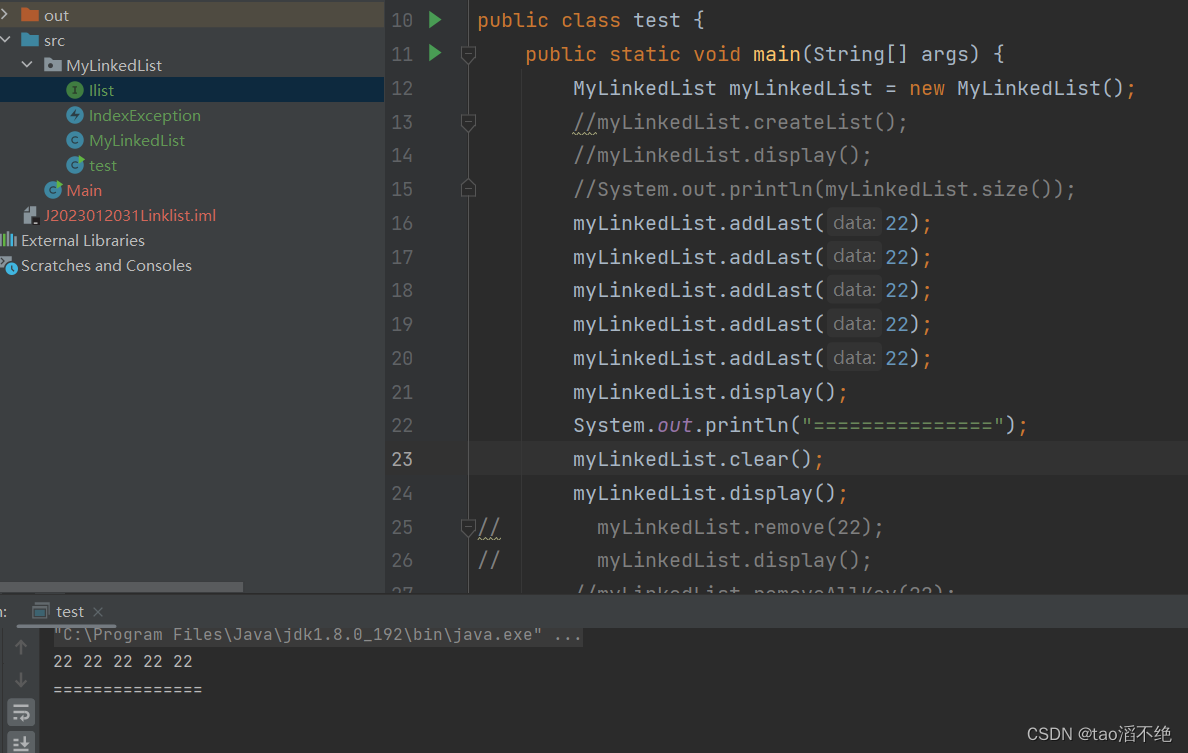
数据结构 模拟实现LinkedList单向不循环链表
目录 一、链表的简单介绍 二、链表的接口 三、链表的方法实现 (1)display方法 (2)size得到单链表的长度方法 (3)addFirst头插方法 (4)addLast尾插方法 (5…...

2023-12-24 LeetCode每日一题(收集足够苹果的最小花园周长)
2023-12-24每日一题 一、题目编号 1954. 收集足够苹果的最小花园周长二、题目链接 点击跳转到题目位置 三、题目描述 给你一个用无限二维网格表示的花园,每一个 整数坐标处都有一棵苹果树。整数坐标 (i, j) 处的苹果树有 |i| |j| 个苹果。 你将会买下正中心坐…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...
