二叉树详解(深度优先遍历、前序,中序,后序、广度优先遍历、二叉树所有节点的个数、叶节点的个数)
目录
一、树概念及结构(了解)
1.1树的概念
1.2树的表示
二、二叉树概念及结构
2.1概念
2.2现实中的二叉树:
2.3数据结构中的二叉树:
2.4特殊的二叉树:
2.5 二叉树的存储结构
2.51 顺序存储:
2.5.2 链式存储:
三、二叉树性质相关选择题练习
四、二叉树的实现
4.1头文件:
4.2Test.c
4.3前序,中序,后序(深度优先遍历)
4.4二叉树所有节点的个数
编辑
4.5叶节点的个数
4.6层序遍历(广度优先遍历,使用队列)
一、树概念及结构(了解)
1.1树的概念
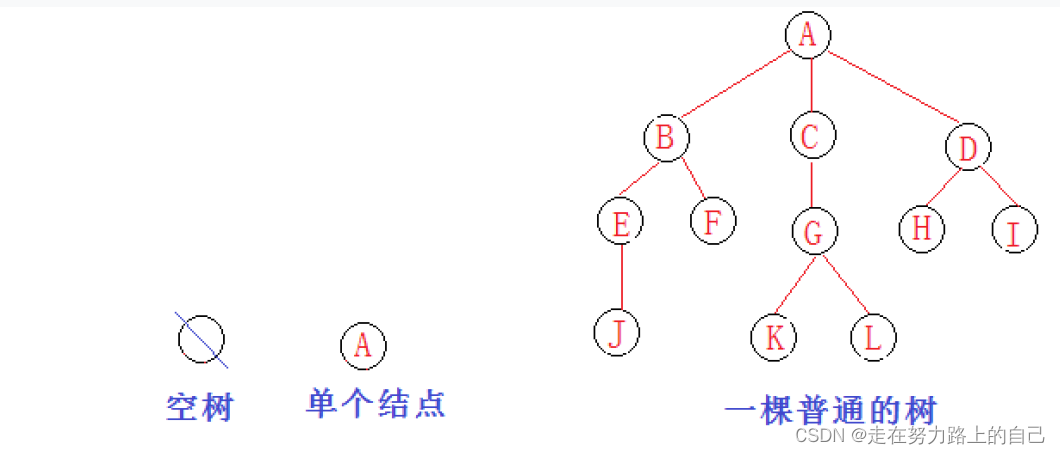
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它
叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
有一个特殊的结点,称为根结点,根节点没有前驱结点除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继,因此,树是递归定义的。



-
节点的度:一个节点含有的子树的个数称为该节点的度; 如下图:A的为6
-
叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I...等节点为叶节点
-
非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G...等节点为分支节点
-
双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B 的父节点
-
孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节 点
-
兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点
-
树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6
-
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
-
树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
关于树的高度,还有一种看法,就是把高度从0开始看,此时树的高度为3。
-
节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
-
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
-
森林:由m(m>0)棵互不相交的多颗树的集合称为森林;(数据结构中的学习并查集本质就是 一个森林)
1.2树的表示
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,实际中树有很多种表示方式,
如:双亲表示法,孩子表示法、孩子兄弟表示法等等。我们这里就简单的了解其中最常用的孩子
兄弟表示法。
typedef int DataType;
struct Node
{
struct Node* _firstChild1; // 第一个孩子结点
struct Node* _pNextBrother; // 指向其下一个兄弟结点
DataType _data; // 结点中的数据域
};

另一种方式:顺序表存孩子的指针(不推荐使用)
struct TreeNode
{
int data;
vector<struct TreeNode*> childs;
}
还有一种表示方式,双亲表示法:
双亲表示法采用顺序表(数组)存储普通树,其实现的核心思想是:顺序存储各个节点的同时,给各节点附加一个记录其父节点位置的变量
#define MAX_SIZE 100 // 宏定义树中结点的最大数量
typedef struct Snode{
char data;
int parent;
} PTNode;
typedef struct{
PTNode tnode[MAX_SIZE]; // 存放树中所有结点
int n; // 结点数
} PTree;

1.3树在实际中的运用(表示文件系统的目录树结构)

二、二叉树概念及结构
2.1概念
一棵二叉树是结点的一个有限集合,该集合或者为空,或者是由一个根节点加上两棵别称为左子
树和右子树的二叉树组成。
二叉树的特点:
1. 每个结点最多有两棵子树,即二叉树不存在度大于2的结点。
2. 二叉树的子树有左右之分,其子树的次序不能颠倒。

2.2现实中的二叉树:

2.3数据结构中的二叉树:


2.4特殊的二叉树:
1. 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉
树。也就是说,如果一个二叉树的层数为K,且结点总数是(2^k) -1 ,则它就是满二叉树。
2. 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对
于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号
从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉
树。


2.5 二叉树的存储结构
二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构。
二叉树的性质
1. 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有2^(i-1) 个结点.
2. 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是2^h- 1.
3. 对任何一棵二叉树, 如果度为0其叶结点个数为 n0, 度为2的分支结点个数为 n2,则有n0=n2
+1
4. 若规定根节点的层数为1,具有n个结点的满二叉树的深度,h=logN + 1
2.51 顺序存储:
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树
会有空间的浪费。而现实中使用中只有堆才会使用数组来存储,关于堆我们后面的章节会专门讲
解。二叉树顺序存储在物理上是一个数组,在逻辑上是一颗二叉树。

2.5.2 链式存储:
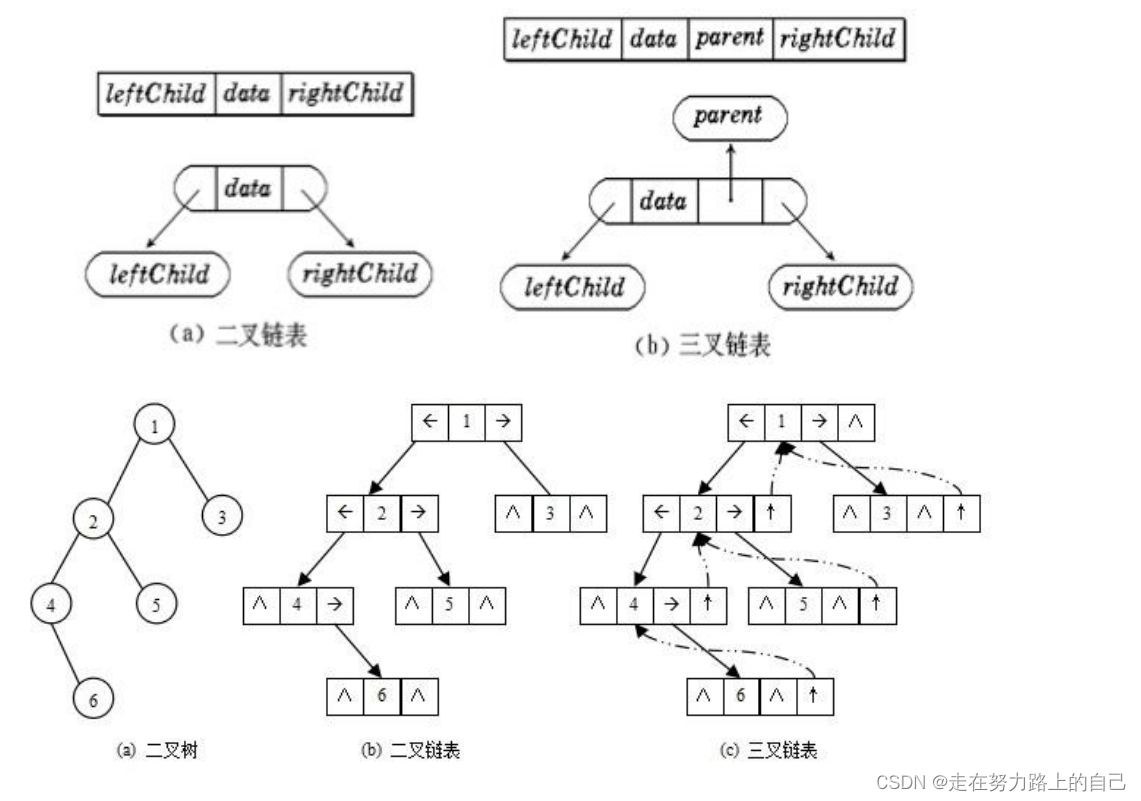
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的
方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩
子和右孩子所在的链结点的存储地址 。链式结构又分为二叉链和三叉链,当前我们学习中一般都
是二叉链,后面课程学到高阶数据结构如红黑树等会用到三叉链。
三、二叉树性质相关选择题练习
1.某完全二叉树按层次输出(同一层从左到右)的序列为 ABCDEFGH 。该完全二叉树的前序序列为(
)
A ABDHECFG
B ABCDEFGH
C HDBEAFCG
D HDEBFGCA
2.二叉树的先序遍历和中序遍历如下:先序遍历:EFHIGJK;中序遍历:HFIEJKG.则二叉树根结点为
()
A E
B F
C G
D H
3.设一课二叉树的中序遍历序列:badce,后序遍历序列:bdeca,则二叉树前序遍历序列为____。
A adbce
B decab
C debac
D abcde

1. 某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为( )
A 不存在这样的二叉树
B 200
C 198
D 199
2.在具有 2n 个结点的完全二叉树中,叶子结点个数为( )
A n
B n+1
C n-1
D n/2
3.一棵完全二叉树的节点数位为531个,那么这棵树的高度为( )
A 11
B 10
C 8
D 12


四、二叉树的实现
4.1头文件:
#pragma once
#include <stdio.h>
#include <stdbool.h>
#include <assert.h>
#include <stdlib.h>typedef int BTDataType;typedef struct BinaryTreeNode
{struct BinaryTreeNode* left;struct BinaryTreeNode* right;BTDataType data;
}BTNode;4.2Test.c
int main()
{BTNode* A = (BTNode*)malloc(sizeof(BTNode));A->data = 'A';A->left = NULL;A->right = NULL;BTNode* B = (BTNode*)malloc(sizeof(BTNode));B->data = 'B';B->left = NULL;B->right = NULL;BTNode* C = (BTNode*)malloc(sizeof(BTNode));C->data = 'C';C->left = NULL;C->right = NULL;BTNode* D = (BTNode*)malloc(sizeof(BTNode));D->data = 'D';D->left = NULL;D->right = NULL;BTNode* E = (BTNode*)malloc(sizeof(BTNode));E->data = 'E';E->left = NULL;E->right = NULL;A->left = B;A->right = C;B->left = D;B->right = E;return 0;
}4.3前序,中序,后序(深度优先遍历)

void PrevOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}printf("%c ", root->data);PrevOrder(root->left);PrevOrder(root->right);
}void InOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}InOrder(root->left);printf("%c ", root->data);InOrder(root->right);
}void PostOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%c ", root->data);}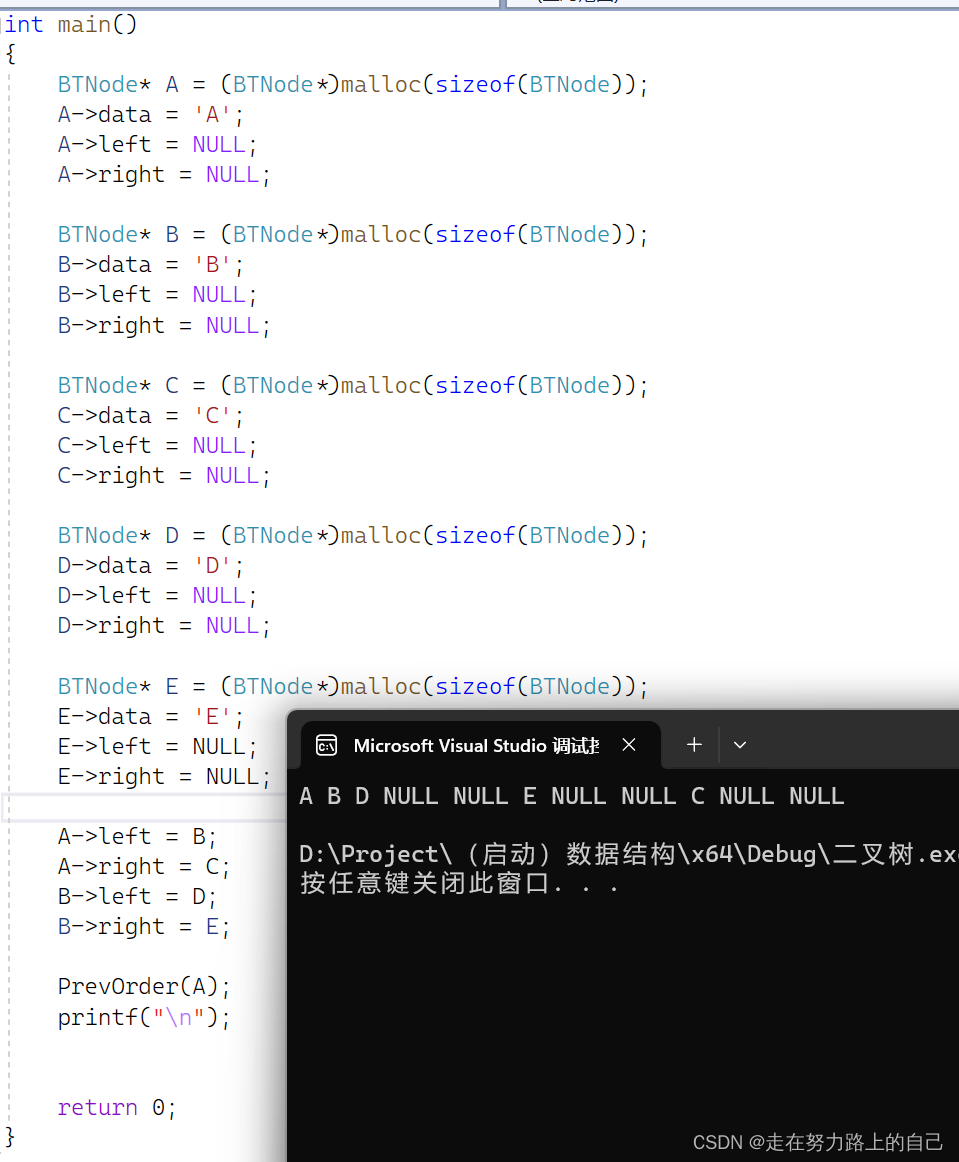
4.4二叉树所有节点的个数

//方法一:定义全局变量(不推荐)
int size = 0;
void TreeSize(BTNode* root)
{if (root == NULL){return;}else {++size;}TreeSize(root->left);TreeSize(root->right);return size;
}方法二:传址调用
int TreeSize(BTNode* root,int* psize)
{if (root == NULL){return;}else {++(*psize);}TreeSize(root->left, psize);TreeSize(root->right, psize);return psize;
}方法三:递归、分治思想:
否则,返回左子树节点数 + 右子树节点数 + 1(当前节点)
int TreeSize(BTNode* root)
{// 如果树为空(即根节点为NULL),则返回0 // 否则,返回左子树节点数 + 右子树节点数 + 1(当前节点)return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}4.5叶节点的个数
int LeafSize(BTNode* root)
{if (root == NULL)return 0;if (root->left == NULL && root->right == NULL)return 1;return TreeSize(root->left) + TreeSize(root->right);}
4.6层序遍历(广度优先遍历,使用队列)


void LevelOrder(BTNode* root)
{Queue q;QueueInit(&q);if (root){QueuePush(&q, root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);printf("%c ", front->data);if (front->left){QueuePush(&q, front->left);}if (front->right){QueuePush(&q, front->right);}}QueueDestory(&q);
}
新年第一篇!!!
祝大家新年快乐

看到这里了还不给博主扣个:
⛳️ 点赞☀️收藏 ⭐️ 关注!
你们的点赞就是博主更新最大的动力!
有问题可以评论或者私信呢秒回哦。
相关文章:

二叉树详解(深度优先遍历、前序,中序,后序、广度优先遍历、二叉树所有节点的个数、叶节点的个数)
目录 一、树概念及结构(了解) 1.1树的概念 1.2树的表示 二、二叉树概念及结构 2.1概念 2.2现实中的二叉树: 2.3数据结构中的二叉树: 2.4特殊的二叉树: 2.5 二叉树的存储结构 2.51 顺序存储: 2.5.2 链式存储&…...
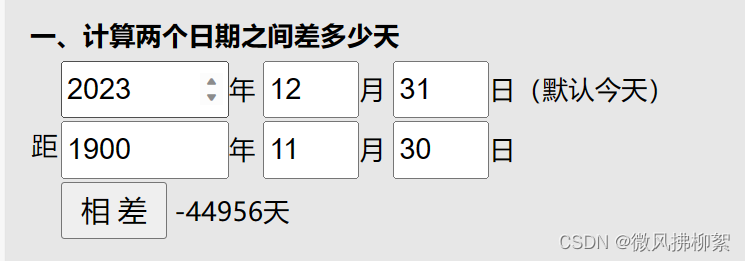
C++日期类的实现
前言:在类和对象比较熟悉的情况下,我们我们就可以开始制作日期表了,实现日期类所包含的知识点有构造函数,析构函数,函数重载,拷贝构造函数,运算符重载,const成员函数 1.日期类的加减…...

B+树的插入删除
操作 插入 case2的原理,非叶子节点永远和最右边的最左边的节点的值相等。 case3:的基本原理 非叶子节点都是索引节点 底层的数据分裂之后 相当于向上方插入一个新的索引(你可以认为非叶子节点都是索引),反正第二层插入160 都要分裂,然后也需要再插入(因为索引部分不需要重…...

c# Avalonia 绘图
在Avalonia UI框架中,绘图主要通过使用DrawingContext类来实现。DrawingContext提供了一系列的绘图API,可以用来绘制线条、形状、图像以及文本等内容。以下是一个简单的示例,说明如何在Avalonia中进行基础的图形绘制 <!-- MainWindow.axa…...

springboot 双数据源配置
1:pom <!--SpringBoot启动依赖--><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-web</artifactId></dependency><dependency><groupId>org.springframework.boot</group…...
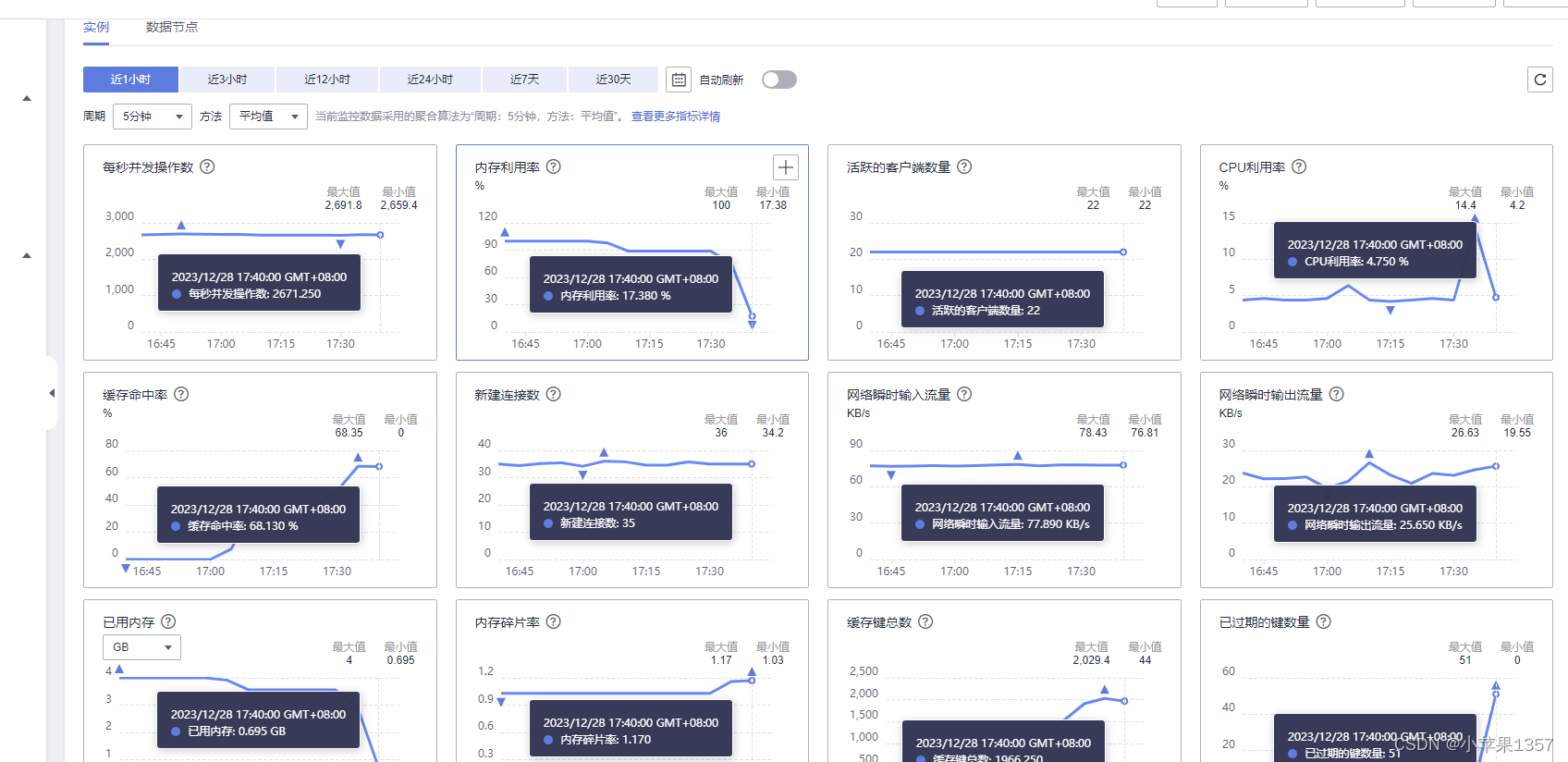
Redis内存使用率高,内存不足问题排查和解决
问题现象 表面现象是系统登录突然失效,排查原因发现,使用redis查询用户信息异常,从而定位到redis问题 if (PassWord.equals(dbPassWord)) {map.put("rtn", 1);map.put("value", validUser);session.setAttribute("…...
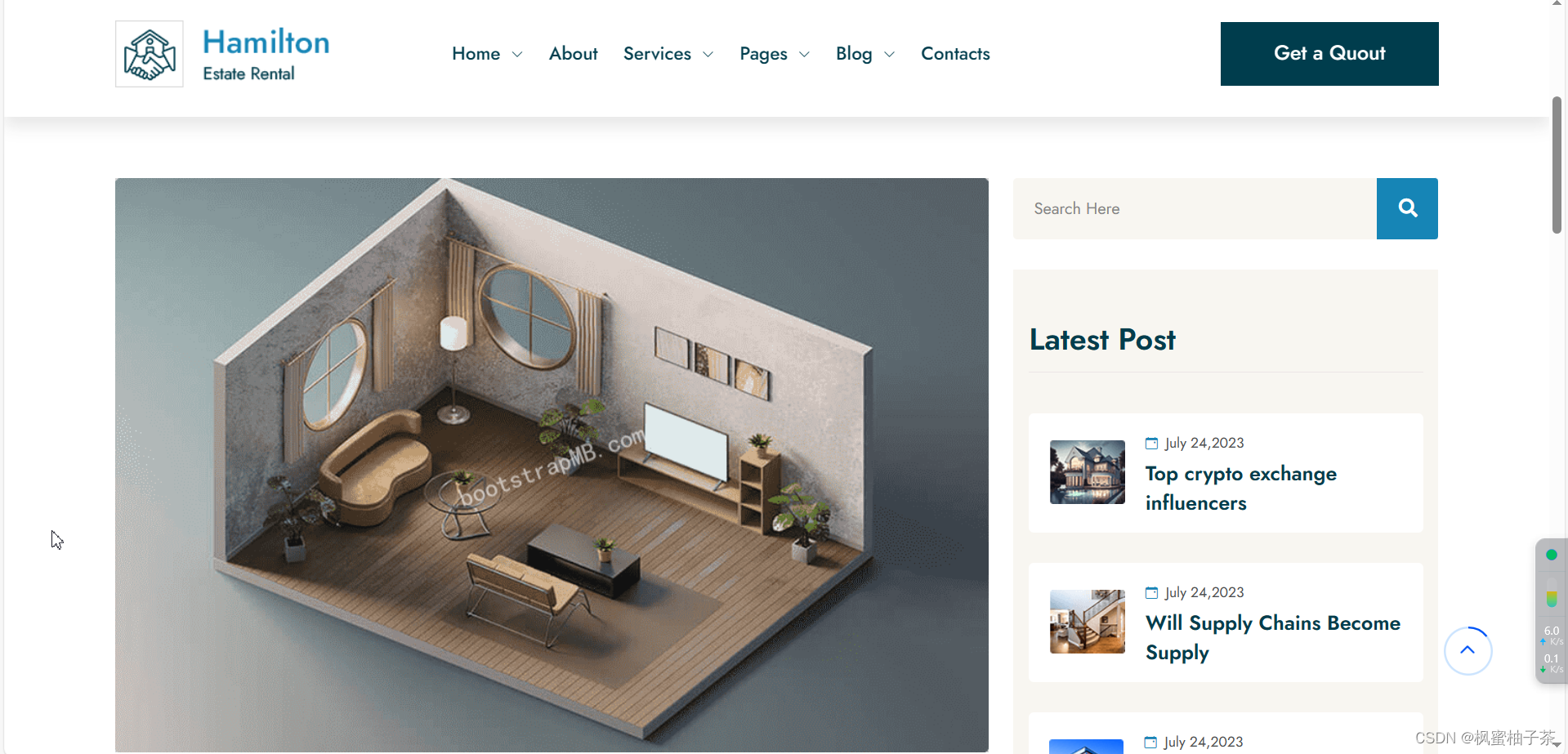
bootstrap5开发房地产代理公司Hamilton前端页面
一、需求分析 房地产代理网站是指专门为房地产行业提供服务的在线平台。这些网站的主要功能是连接房地产中介机构、房产开发商和潜在的买家或租户,以促成买卖或租赁房产的交易。以下是一些常见的房地产代理网站的功能: 房源发布:房地产代理网…...
2024年Mac专用投屏工具AirServer 7 .27 for Mac中文版
AirServer 7 .27 for Mac中文免费激活版是一款Mac专用投屏工具,能够通过本地网络将音频、照片、视频以及支持AirPlay功能的第三方App,从 iOS 设备无线传送到 Mac 电脑的屏幕上,把Mac变成一个AirPlay终端的实用工具。 目前最新的AirServer 7.2…...

关于MySql字段类型的实践总结
当字段为数值类型时应使用无符号UNSIGNED修饰 ALTER TABLE infoMODIFY COLUMN user_id int UNSIGNED NOT NULL; 当字段为varchar类型时应注意是否选择合适的字符集 例如存储一些范围值,数字英文字符时(IP、生日、客户端标识等或以“,”分隔的数据&…...
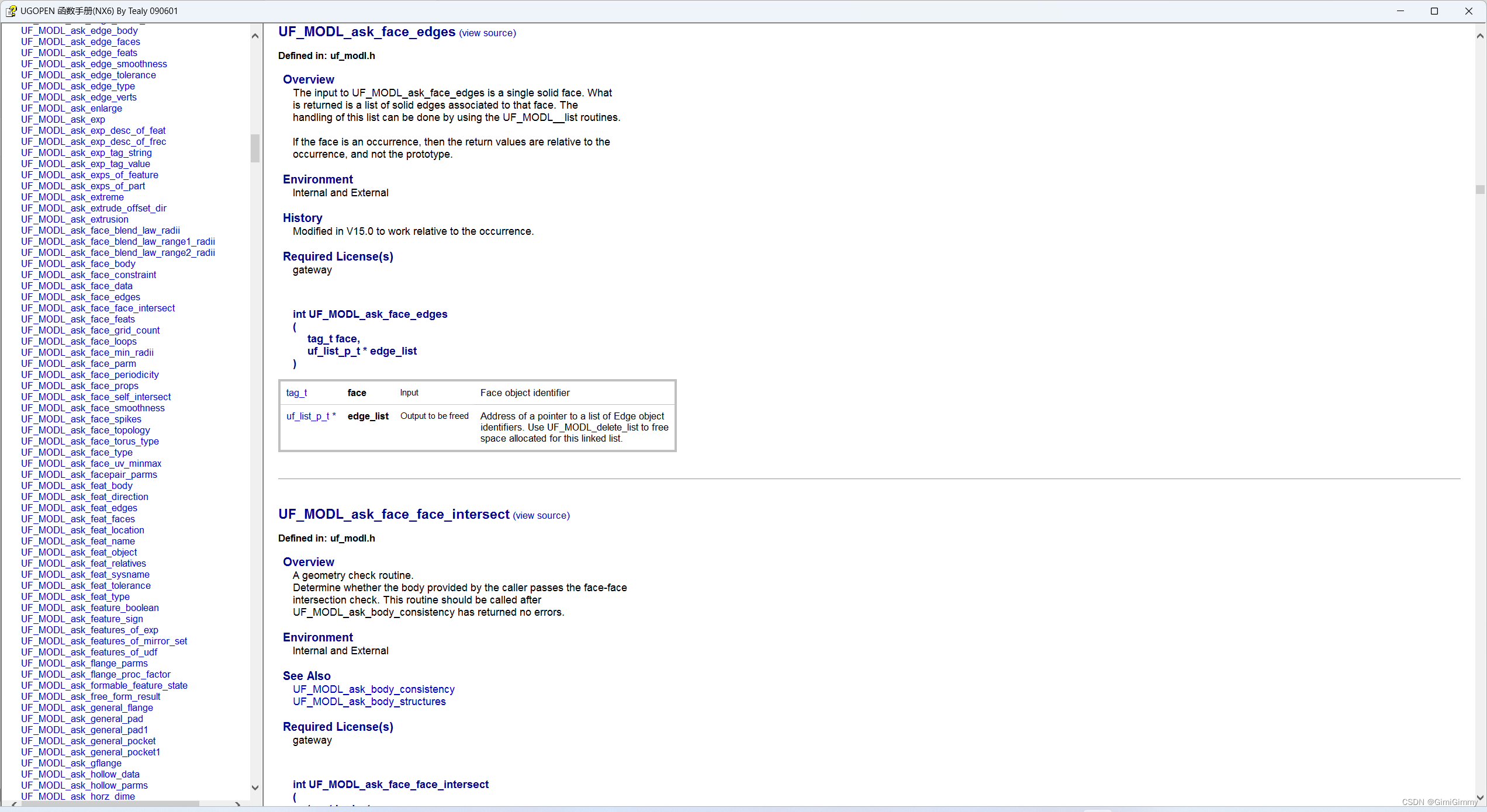
UG NX二次开发(C#)-Ufun和NXOpen混合编程
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 1、前言2、Ufun函数3、 NXOpen4、混合编程实现1、前言 在UG NX二次开发过程中,采用Ufun功能比较简单,能用比较少的代码实现我们需要的功能,但是ufun函数的功能不是很强大,尤其随着UG NX的版本…...
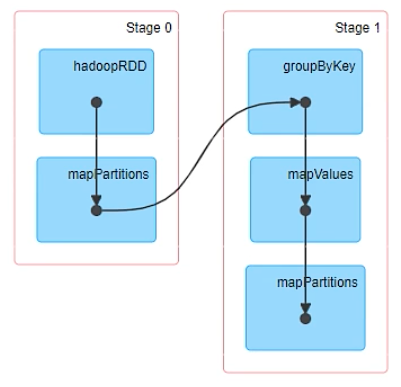
【Spark精讲】一文讲透Spark RDD
MapReduce的缺陷 MR虽然在编程接口的种类和丰富程度上已经比较完善了,但这些系统普遍都缺乏操作分布式内存的接口抽象,导致很多应用在性能上非常低效 。 这些应用的共同特点是需要在多个并行操 作之间重用工作数据集 ,典型的场景就是机器学习…...

如在MT9040、IDT82V3001A 等锁相环上电后或输入参考频率改变后必须复位锁相环。
锁相环是一种反馈控制系统,它能够将输出信号的相位锁定到输入参考信号的相位上。在实际应用中,如MT9040、IDT82V3001A等PLL集成电路在上电后或者当输入参考频率发生变化后通常需要复位的原因涉及到几个方面: 1、初始化状态: 当PLL电路上电时,其内部的各个组件可能…...

构建安全的SSH服务体系
某公司的电子商务站点由专门的网站管理员进行配置和维护,并需要随时从Internet进行远程管理,考虑到易用性和灵活性,在Web服务器上启用OpenSSH服务,同时基于安全性考虑,需要对 SSH登录进行严格的控制,如图10…...

wpf ComboBox绑定数据及变更事件
定义ComboBox,以及SelectionChanged事件 <ComboBox x:Name"cmb_radius" Height"30" Width"65" FontSize"15" DisplayMemberPath"Value" SelectedValuePath"Key" HorizontalAlignment"Center&…...

SQL BETWEEN 操作符
BETWEEN 操作符选取介于两个值之间的数据范围内的值。这些值可以是数值、文本或者日期。 SQL BETWEEN 语法 SELECT column1, column2, ... FROM table_name WHERE column BETWEEN value1 AND value2; 参数说明: column1, column2, ...:要选择的字段名…...

Java位运算及移位运算
java中能表示整数数据类型的有byte、short、char、int、long,在计算机中占用的空间使用字节描述,1个字节使用8位二进制表示。 数据类型字节数二进制位数表示范围默认值byte18-27 – 27-10char2160 – 216-1\u0000 (代表字符为空 转成int就是0)short216-…...
)
上界通配符(? extends Type)
在Java中,? extends Type是一个上界通配符,表示参数化类型的上限是Type。这意味着容器可以持有Type类型的任何对象或者Type的子类型对象。 使用场景 这种类型的通配符常用于泛型方法中,允许方法接受Type的实例或其子类型的集合。这同样基于…...
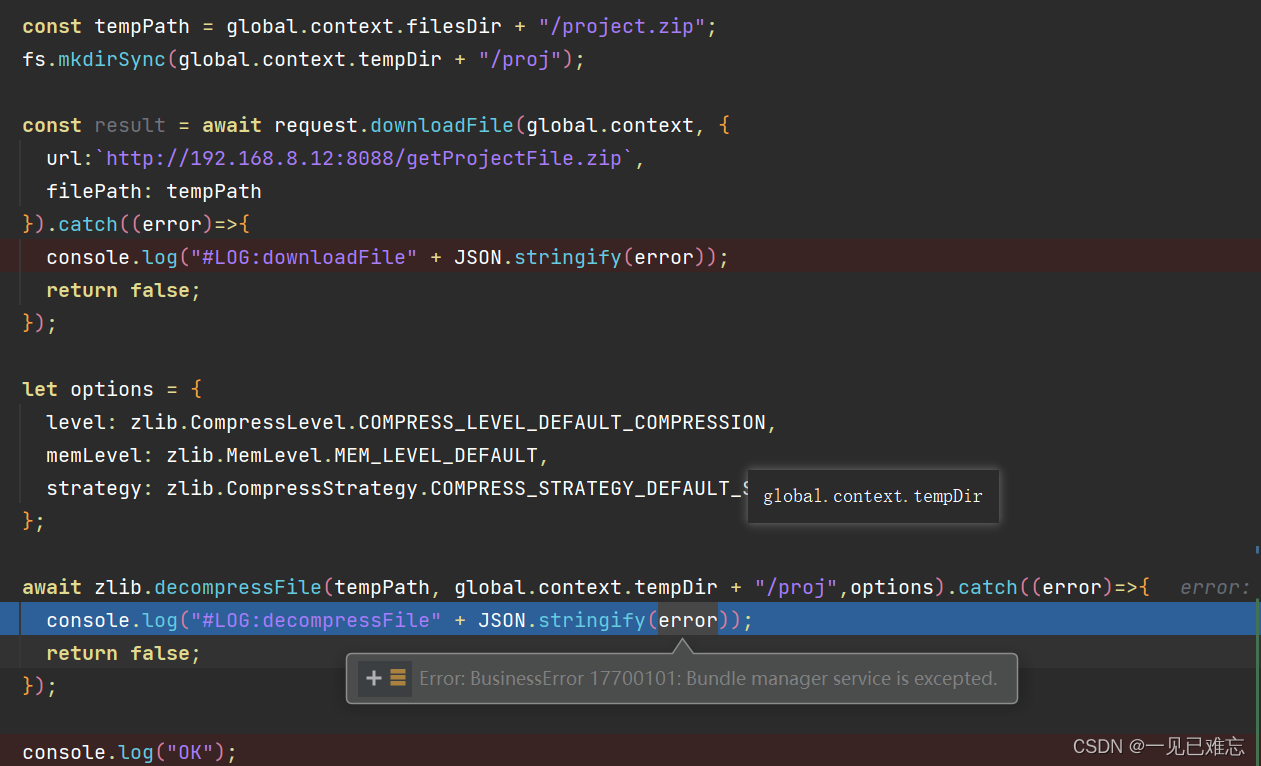
zlib.decompressFile报错 【Bug已解决-鸿蒙开发】
文章目录 项目场景:问题描述原因分析:解决方案:方案1方案2此Bug解决方案总结寄语项目场景: 最近也是遇到了这个问题,看到网上也有人在询问这个问题,本文总结了自己和其他人的解决经验,解决了zlib.decompressFile报错 的问题。 问题: zlib.decompressFile报错,怎么解…...

54.网游逆向分析与插件开发-游戏增加自动化助手接口-项目需求与需求拆解
内容来源于:易道云信息技术研究院VIP课 项目需求: 为游戏增加VIP功能-自动化助手。自动化助手做的是首先要说一下背景,对于授权游戏来讲它往往年限都比较老,老游戏和新游戏设计理念是不同的,比如说老游戏基本上在10年…...

Spring Boot笔记2
3. SpringBoot原理分析 3.1. 起步依赖原理解析 3.1.1. 分析spring-boot-starter-parent 按住Ctrl键,然后点击pom.xml中的spring-boot-starter-parent,跳转到了spring-boot-starter-parent的pom.xml,xml配置如下(只摘抄了部分重…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...

内窥镜检查中基于提示的息肉分割|文献速递-深度学习医疗AI最新文献
Title 题目 Prompt-based polyp segmentation during endoscopy 内窥镜检查中基于提示的息肉分割 01 文献速递介绍 以下是对这段英文内容的中文翻译: ### 胃肠道癌症的发病率呈上升趋势,且有年轻化倾向(Bray等人,2018&#x…...

