国科大图像处理2023速通期末——汇总2017-2019
国科大2023.12.28图像处理0854期末重点
图像处理 王伟强 作业 课件 资料
一、填空
- 一个阴极射线管它的输入与输出满足 s = r 2 s=r^{2} s=r2,这将使得显示系统产生比希望的效果更暗的图像,此时伽马校正通常在信号进入显示器前被进行预处理,令p与q表示伽马校正的输入与输出,则p与q之间的映射关系式表示为: q = p 1 2 q=p^{\frac{1}{2}} q=p21
- 卷积是一种图像处理领域最有影响力的计算之一,对于一幅输入图像f(x,y), 我们可以通过卷积运算产生一幅新的图像g(x,y),若g(x,y)=0.1f(x+1,y)+0.2f(x-1y)+0.3f(x,y)+0.2f(x,y-1)+0.2f(x,y+1)这里x表示行标,y表示图像中像素位置的列坐标,请用一个3X3的矩阵来表示这个卷积核
- 我们处理一幅图像可以在空域中通过线性滤波运算进行处理,也可以在频域内对它进行处理达到同样的效果。该事实的理论基础就是基于傅立叶变换的卷积定理,若我们用f(x,y),g(x,y)表示图像与线性滤波核,它们对应的傅立叶变换分别用F(u,v),G(u,v)表示则该定理可形式化描述为f(x,y)∗g(x,y)⟷F(u,v)×G(u,v)
- 拉普拉斯波器的频域表示的函数形式为 H ( u , v ) = − 4 π 2 ( u 2 + v 2 ) H(u,v)=-4\pi ^{2}(u^{2}+v^{2}) H(u,v)=−4π2(u2+v2)
- 假设我们有一个在0-1区间的均匀分布随机数发生器w,若已知一个满足瑞利分布的随机变量累加分布函数CDF是 F z ( z ) = { 1 − e x p ( − ( z − a ) 2 b ) , z ≥ a 0 , z < a F_{z}(z)=\begin{cases} 1-\frac{exp(-(z-a)^{2}}{b}),z\ge a\\ 0,z<a \end{cases} Fz(z)={1−bexp(−(z−a)2),z≥a0,z<a,则基于w的瑞利分布的随机数发生器z的方程为 z = a + − b l n ( 1 − w ) z=a+\sqrt{-bln(1-w)} z=a+−bln(1−w)
- 若高斯低通滤波器在频域中的表示为 H ( u , v ) = e − D 2 ( u , v ) 2 D 0 2 H(u,v)=e^{-\frac{D^{2}(u,v)}{2D_{0}^{2}}} H(u,v)=e−2D02D2(u,v)则对应的高斯高通滤波器在频域中的表示为 H h ( u , v ) = 1 − e − D 2 ( u , v ) 2 D 0 2 H_{h}(u,v)=1-e^{-\frac{D^{2}(u,v)}{2D_{0}^{2}}} Hh(u,v)=1−e−2D02D2(u,v)
- Weiner 滤波的计算方法为 F ( u , v ) = [ 1 H ( u , v ) ⋅ ∣ H ( u , v ) ∣ 2 ∣ H ( u , v ) ∣ 2 + S η ( x , y ) S f ( x , y ) ] G ( u , v ) ) F(u,v)=[\frac{1}{H(u,v)}·\frac{|H(u,v)|^{2}}{|H(u,v)|^{2}+\frac{S_{\eta }(x,y)}{S_{f}(x,y)}}]G(u,v)) F(u,v)=[H(u,v)1⋅∣H(u,v)∣2+Sf(x,y)Sη(x,y)∣H(u,v)∣2]G(u,v))其中 S η ( x , y ) S_{\eta }(x,y) Sη(x,y)代表噪声功率谱密度,H(u,v)代表退化函数
- YCbCr中的Y代表明度,Cb与Cr代表蓝色与红色的浓度偏移,HSV中的H代表色调,s代表饱和度
二、选择
-
采用对比度拉伸是实现灰度图像的增强的一种重要思路,而分段线性变换函数是一种常被采用的技术。针对某一段输入灰度范围,若你想扩大输出灰度的动态范围,所构造的那一段线性映射函数的斜率k应满足:(A)
A.k>1
B.k=1
C.k<1
D.取任何值都可以 -
若一幅图像中存在椒盐噪声,下面哪种滤波器可选择来去除它们:(D)
A.算术均值滤波器
B.反调和滤波器
C.拉普拉斯滤波器
D.中值滤波器 -
通过卷积运算对图像进行各种目的的滤波是图像处理的重要内容。对于离散的两个一维信号[3,5,6],g=[1,-1],对应的卷积结果是(A)
A.[3,2,1,-6]
B.[2.1]
C.[-3,-2-1,6]
D.[-2,-1] -
高斯低通滤波器 H ( u , v ) = e − D 2 ( u , v ) 2 D 0 2 H(u,v)=e^{-\frac{D^{2}(u,v)}{2D_{0}^{2}}} H(u,v)=e−2D02D2(u,v)中存在一个参数 D 0 D_{0} D0,对于一幅中年妇女面部特写图像,若发现采用 D 0 = 100 D_{0}=100 D0=100时,去除该妇女眼部的皱纹不彻底,则应该:(A)
A.适当减小 D 0 D_{0} D0
B.适当加大 D 0 D_{0} D0
C.保持 D 0 D_{0} D0不变
D.前面选项都不对 -
对于一个具有正交性质的完美重建滤波器组,若它的滤波器之间具有如下的关系:(B)
g 1 ( n ) = ( − 1 ) n g 0 ( 2 K − 1 − n ) , h 1 ( n ) = g 1 ( 2 K − 1 − n ) , i = 0 , 1 g_{1}(n)=(-1)^{n}g_{0}(2K-1-n),h_{1}(n)=g_{1}(2K-1-n),i=0,1 g1(n)=(−1)ng0(2K−1−n),h1(n)=g1(2K−1−n),i=0,1A. ( − 1 ) n h 0 ( 2 K − 1 − n ) (-1)^{n}h_{0}(2K-1-n) (−1)nh0(2K−1−n)
B. ( − 1 ) n + 1 h 0 ( 2 K − 1 − n ) (-1)^{n+1}h_{0}(2K-1-n) (−1)n+1h0(2K−1−n)
C. ( − 1 ) n h 0 ( n ) (-1)^{n}h_{0}(n) (−1)nh0(n)
D. ( − 1 ) n + 1 h 0 ( n ) (-1)^{n+1}h_{0}(n) (−1)n+1h0(n) -
信息论是信息压缩的理论基础,而互信息是信息论中一个非常重要的概念,信源z与信道输出v之间互信息I(z,v)的意义为©
A.信源z与信道输出v间的平均信息量
B.观察单一信道输出符号时接收到的平均信息
C.观测到输出v后信源符号的平均信息量
D信道可靠传输信息的最大传送率
三、判断
- 对一幅数字图像进行一次直方图均衡处理后,通常不会产生非常绝对平的直方图。即便我们对处理后的图像再进行一次直方图处理,理论上也不会产生任何效果。(√)
- 拉普拉斯滤波器与统计排序滤波器均不是一种卷积运算。(×)
- 卷积运算具有交换性与结合性。(√)
- 低通高阶巴特沃斯滤波器存在振铃效应,而低通高斯滤波器不存在振铃效应。(√)
- 我们可以用阶数Q<0的逆谐波均值滤波器来去除盐噪声。(√)
- 给定一幅图像,若我们能准确估计噪声的均值与方差,则可以知道噪声的能量(所有像素位置的噪声强度的平方和)。(√)
- 在图像编码中,涉及信源编码与信道编码,两者都是为了实现信息的压缩表示。(×)
- 对于一个事件,它发生的概率越小,它的熵越大。(√)
- 若一幅图像中含有一些噪声点或干扰性微小结构,可采用形态处理中的开操作作为一种处理段来去除它。(√)
四、简答
1. 简述什么是线性移不变系统
答:线性移不变性系统(Linear Shift-Invariant System,简称LSI系统)是一种特殊的系统,它对输入图像的处理满足线性和移不变性两个条件。
- 线性:系统对输入图像的处理是线性的,即如果输入图像是两个图像的线性组合,那么输出图像也是这两个图像经过系统处理后的输出的相同线性组合。数学上表示为,如果 f 1 ( x , y ) f_{1}(x,y) f1(x,y)和 f 2 ( x , y ) f_{2}(x,y) f2(x,y)是两个输入图像,α和β是任意常数,那么系统的输出满足: S ( α f 1 + β f 2 ) = α S ( f 1 ) + β S ( f 2 ) S(αf_{1}+βf_{2})=αS(f_{1})+βS(f_{2}) S(αf1+βf2)=αS(f1)+βS(f2)
- 移不变性:系统对输入图像的处理是移不变的,即如果输入图像在空间域内平移,那么输出图像也会相应地平移,而不会改变其它特性。数学上表示为,如果f(x,y)是输入图像, ( x 0 , y 0 ) (x_{0},y_{0}) (x0,y0)是平移量,那么系统的输出满足: H [ f ( x , y ) ] = g ( x , y ) , H [ f ( x − x 0 , y − y 0 ) ] = g ( x − x 0 , y − y 0 ) H[f(x,y)]=g(x,y),H[f(x-x_{0},y-y_{0})]=g(x-x_{0},y-y_{0}) H[f(x,y)]=g(x,y),H[f(x−x0,y−y0)]=g(x−x0,y−y0)
线性移不变性系统的一个重要特性是,它们可以通过卷积运算来描述。对于任何LSI系统,都存在一个称为系统冲激响应的函数 h ( x , y ) h(x,y) h(x,y),使得系统对任何输入图像 f ( x , y ) f(x,y) f(x,y) 的输出 g ( x , y ) g(x,y) g(x,y)可以表示为 f ( x , y ) f(x,y) f(x,y)和 h ( x , y ) h(x,y) h(x,y)的卷积: g ( x , y ) = f ( x , y ) ∗ h ( x , y ) g(x,y)=f(x,y)\ast h(x,y) g(x,y)=f(x,y)∗h(x,y)
2. 观察如下所示图像。右边的图像这样得到:
(a)在原始图像左边乘以 ( − 1 ) x + y (-1)^{x+y} (−1)x+y;
(b) 计算离散傅里叶变换(DFT);
© 对变换取复共轭;
(d) 计算傅里叶反变换;
(e) 结果的实部再乘以 ( − 1 ) x + y (-1)^{x+y} (−1)x+y。
(用数学方法解释为什么会产生右图的效果)。DIP旋转了180度
假设原图像为 f 1 ( x , y ) f_{1}(x,y) f1(x,y)
- 经过a操作变为 ( − 1 ) x + y f 1 ( x , y ) (-1)^{x+y}f_{1}(x,y) (−1)x+yf1(x,y)
- 经过b操作离散傅里叶变换变为 F ( u , v ) = 1 M N ∑ u = 0 M − 1 ∑ v = 0 N − 1 ( − 1 ) x + y f ( x , y ) e − j 2 π ( u x M + u y N ) F(u,v)=\frac{1}{MN}\sum_{u=0}^{M-1}\sum_{v=0}^{N-1}{(-1)^{x+y}f(x,y)e^{-j2\pi\left(\frac{ux}{M}+\frac{uy}{N}\right)}} F(u,v)=MN1∑u=0M−1∑v=0N−1(−1)x+yf(x,y)e−j2π(Mux+Nuy)
- 通过c操作,根据傅里叶变换性值
- F ∗ ( u , v ) = 1 M N ∑ u = 0 M − 1 ∑ v = 0 N − 1 ( − 1 ) x + y f ( x , y ) e j 2 π ( u x M + u y N ) F^\ast (u,v)=\frac{1}{MN}\sum_{u=0}^{M-1}\sum_{v=0}^{N-1}{(-1)^{x+y}f(x,y)e^{j2\pi\left(\frac{ux}{M}+\frac{uy}{N}\right)}} F∗(u,v)=MN1∑u=0M−1∑v=0N−1(−1)x+yf(x,y)ej2π(Mux+Nuy)
- 通过d操作得傅里叶反变换变为
- I D F T ( F ∗ ( u , v ) ) = 1 M N ∑ u = 0 M − 1 ∑ v = 0 N − 1 [ 1 M N ∑ u = 0 M − 1 ∑ v = 0 N − 1 ( − 1 ) x + y f ( x , y ) e j 2 π ( u x M + u y N ) ] e j 2 π ( u x M + u y N ) IDFT(F^\ast (u,v))=\frac{1}{MN}\sum_{u=0}^{M-1}\sum_{v=0}^{N-1}[\frac{1}{MN}\sum_{u=0}^{M-1}\sum_{v=0}^{N-1}{(-1)^{x+y}f(x,y)e^{j2\pi\left(\frac{ux}{M}+\frac{uy}{N}\right)}}]e^{j2\pi\left(\frac{ux}{M}+\frac{uy}{N}\right)} IDFT(F∗(u,v))=MN1∑u=0M−1∑v=0N−1[MN1∑u=0M−1∑v=0N−1(−1)x+yf(x,y)ej2π(Mux+Nuy)]ej2π(Mux+Nuy)实部为 ( − 1 ) x + y f ( − x , − y ) (-1)^{x+y}f(-x,-y) (−1)x+yf(−x,−y)
- e操作后变为 ( − 1 ) x + y ( − 1 ) x + y f ( − x , − y ) = f ( − x , − y ) (-1)^{x+y}(-1)^{x+y}f(-x,-y)=f(-x,-y) (−1)x+y(−1)x+yf(−x,−y)=f(−x,−y)
效果原图像旋转180°
3. 描述如何构建高斯金字塔与拉普拉斯金字塔
-
高斯金字塔建立:
- 生成初始图像(最底层): 将原始图像 f ( x , y ) f(x,y) f(x,y)作为金字塔的第一层。
- 进行下采样: 对当前层的图像进行高斯滤波,然后进行下采样,即去除一些行和列,以生成下一层的图像。下采样可以使用像素平均值或其他插值技术。下采样的目的是减小图像的尺寸。
- 重复步骤2: 重复进行高斯滤波和下采样,直到达到金字塔的顶层。每一层的图像尺寸都比前一层的尺寸小。
-
拉普拉斯金字塔建立:
- 生成高斯金字塔: 使用上述方法生成高斯金字塔。
- 构建拉普拉斯金字塔: 拉普拉斯金字塔的每一层都是由对应的高斯金字塔层与该层的上一层进行差分得到的。即,拉普拉斯金字塔的每一层是由高斯金字塔的对应层减去该层的上一层。对于每一层i,拉普拉斯金字塔的图像 L i L_{i} Li可以用以下公式表示: L i = G i − e x p a n e d ( G i + 1 ) L_{i}=G_{i}-expaned(G_{i+1}) Li=Gi−expaned(Gi+1)
其中, G i G_{i} Gi是高斯金字塔的第 i 层,expaned是上采样操作。这样,我们得到的拉普拉斯金字塔的第一层是高斯金字塔的最顶层,最后一层是高斯金字塔的最底层
4. 每一个小波的尺度函数都遵循Mallat提出的多分辨率分析的4个基本要求,请描述这4个基本要求的内容
答:
- 尺度函数对它的整数平移对应的函数是正交的
- 哈尔函数被称为是紧支撑的,意味着除了称为支撑域有限区间外,函数值都为0
- 必须注意,当尺度函数的支撑域大于1时,整数平移函数间的正交性将变得更加难于被满足 - 低尺度尺度函数张成的子空间包含于高尺度尺度函数张成的子空间内
V − ∞ ⊂ . . . ⊂ V − 1 ⊂ V − 0 ⊂ V 1 ⊂ . . . ⊂ V + ∞ V_{-∞} \subset ... \subset V_{-1}\subset V_{-0}\subset V_{1}\subset ...\subset V_{+∞} V−∞⊂...⊂V−1⊂V−0⊂V1⊂...⊂V+∞ - 唯一包含在 V j V_{j} Vj所有中的函数是f(x)=0
V − ∞ = 0 V_{-∞}=0 V−∞=0 - 任何函数都可以以任意精度表示 V ∞ = L 2 ( R ) V_{∞}=L^{2}(R) V∞=L2(R)
5. 傅里叶变换的6个性质
- 空域频移性 F [ f ( x − x 0 , y − y 0 ) ] = F ( u , v ) e − j 2 π ( u x 0 M + v y 0 N ) \mathscr{F}[f(x-x_{0},y-y_{0})]=F(u,v)e^{-j2\pi (\frac{ux_{0}}{M}+\frac{vy_{0}}{N})} F[f(x−x0,y−y0)]=F(u,v)e−j2π(Mux0+Nvy0)
- 时域频移性 F [ f ( x , y ) e − j 2 π ( u x 0 M + v y 0 N ) ] = F ( u − u 0 , v − v 0 ) \mathscr{F}[f(x,y)e^{-j2\pi (\frac{ux_{0}}{M}+\frac{vy_{0}}{N})}]=F(u-u_{0},v-v_{0}) F[f(x,y)e−j2π(Mux0+Nvy0)]=F(u−u0,v−v0)
- F [ f ( x , y ) ( − 1 ) x + y ] = F ( u − M 2 , v − N 2 ) \mathscr{F}[f(x,y)(-1)^{x+y}]=F(u-\frac{M}{2},v-\frac{N}{2}) F[f(x,y)(−1)x+y]=F(u−2M,v−2N) - 平均和对称
- 平均 F ( 0 , 0 ) = 1 M N ∑ u = 0 M − 1 ∑ v = 0 N − 1 f ( x , y ) F(0,0)=\frac{1}{MN}\sum_{u=0}^{M-1}\sum_{v=0}^{N-1}{f(x,y)} F(0,0)=MN1∑u=0M−1∑v=0N−1f(x,y)
- 共轭 F ( u , v ) = F ∗ ( − u , − v ) F(u,v)=F^{\ast}(-u,-v) F(u,v)=F∗(−u,−v)
- 对称 ∣ F ( u , v ) ∣ = ∣ F ( − u , − v ) ∣ |F(u,v)|=|F(-u,-v)| ∣F(u,v)∣=∣F(−u,−v)∣
- 可分离性 F ( u , v ) = F f ( x , y ) = ∑ y [ ∑ x f ( x , y ) e − j 2 π x u M ] e − j 2 π y v N = ∑ y F ( u , y ) e − j 2 π y v N F(u,v)=\mathscr{F}f(x,y)=\sum_{y}[\sum_{x}{f(x,y)e^{-j2\pi \frac{xu}{M}}}]e^{-j2\pi \frac{yv}{N}}=\sum_{y}F(u,y)e^{-j2\pi \frac{yv}{N}} F(u,v)=Ff(x,y)=∑y[∑xf(x,y)e−j2πMxu]e−j2πNyv=∑yF(u,y)e−j2πNyv
- 旋转性 x = r c o s θ , y = r s i n θ , u = ω c o s φ , v = ω s i n φ x=rcosθ ,y=rsinθ , u=\omega cos\varphi , v=\omega sin\varphi x=rcosθ,y=rsinθ,u=ωcosφ,v=ωsinφ
f ( r , θ + θ 0 ) ⇔ F ( ω , φ + θ 0 ) f(r,θ+θ_{0})\Leftrightarrow F(\omega,\varphi+θ_{0}) f(r,θ+θ0)⇔F(ω,φ+θ0) - 周期性f(x,y)=f(x+M,y)=f(x,y+N)=f(x+M,y+N)
F(u,v)=F(u+M,v)=F(u,v+N)=F(u+M,v+N) - 线性 F ( a f ( x , y ) + b g ( x , y ) ) = a F ( f ( x , y ) ) + b F ( g ( x , y ) ) \mathscr{F} (af(x,y)+bg(x,y))=a\mathscr{F} (f(x,y))+b\mathscr{F}(g(x,y)) F(af(x,y)+bg(x,y))=aF(f(x,y))+bF(g(x,y))
- 微分性
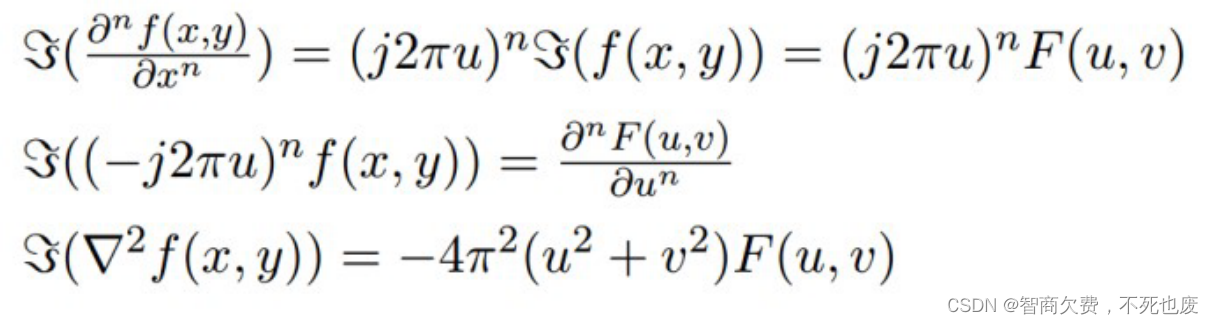
6. 请用集合的语言描述形态学中的腐蚀与膨胀,并用进一步用数学公式定义开运算与闭运算。
假设 A 是一个图像集合,并且 B 是一个称为结构元素的集合。
-
腐蚀(Erosion):
腐蚀操作可以看作是将结构元素 B 从图像 A 中滑动,只要 B 完全覆盖A 的某一部分,那么该部分就被保留,否则就被去除。
数学表述为: A ⊖ B = { z ∣ ( B ) z ⊆ A } A⊖B=\left \{ z∣(B)_{z}\subseteq A \right \} A⊖B={z∣(B)z⊆A}
⊖ 表示腐蚀操作, ( B ) z (B)_{z} (B)z表示将结构元素 B 的原点放在 z 处。 -
膨胀(Dilation):
膨胀操作可以看作是将结构元素 B 从图像 A 中滑动,只要B 与 A 有交集,那么该部分就被保留。
数学表述为: A ⊕ B = { z ∣ ( B ) z ⊆ A } A⊕B=\left \{ z∣(B)_{z}\subseteq A \right \} A⊕B={z∣(B)z⊆A}⊕ 表示膨胀操作 -
开运算(Opening):
开运算首先对图像进行腐蚀,然后再进行膨胀。这通常用于消除小的对象或噪声。
数学表述为: A ∘ B = ( A ⊕ B ) ⊖ B A∘B=(A⊕B)⊖B A∘B=(A⊕B)⊖B -
闭运算(Closing):
闭运算首先对图像进行膨胀,然后再进行腐蚀。这通常用于填充小的孔洞或连接不连续的对象。
数学表述为: A ⋅ B = ( A ⊖ B ) ⊕ B A·B=(A⊖B)⊕B A⋅B=(A⊖B)⊕B
7. 简述拉普拉斯算子、拉普拉斯算子的傅里叶变换?
五、计算
1.直方图均衡
一幅具有8个灰度级的图像的归一化直方图为[0.17 0.25 0.21 0.16 0.07 0.08 0.04 0.02],求直方图均衡后的灰度级和对应概率,并画出均衡后归一化直方图的示意图。
2. Z 变换证明
Z变换是一种信号分析的重要工具。它有许多重要的性质,请对如下性质进行证明:
- (1)若x(n)的Z变换为X(z),则 ( − 1 ) n x ( n ) (-1)^{n}x(n) (−1)nx(n)的Z变换为 X(-z)
- (2)若x(n)的Z变换为X(z),则 x(-n)的Z变换为 X ( 1 z ) X(\frac{1}{z}) X(z1)
- (3)若x(n)的Z变换为X(z),则下x(2n)的Z变换为 1 2 [ X ( z 1 2 ) + X ( − z 1 2 ) ] \frac{1}{2}[X(z^\frac{1}{2})+X(-z^\frac{1}{2})] 21[X(z21)+X(−z21)]
证明:已知x(n)的Z变换为: X ( Z ) = ∑ − ∞ ∞ x ( n ) z − n X(Z)=\sum_{-\infty}^{\infty}{x(n)z^{-n}} X(Z)=∑−∞∞x(n)z−n-
( − 1 ) n x ( n ) {(-1)}^nx(n) (−1)nx(n)的Z变换为:
∑ − ∞ ∞ ( − 1 ) n x ( n ) z − n = ∑ − ∞ ∞ ( − 1 ) − n x ( n ) z − n = ∑ − ∞ ∞ x ( n ) ( − z ) − n = X ( − z ) \sum_{-\infty}^{\infty}{\left(-1\right)^{n}x\left(n\right)z^{-n}}=\sum_{-\infty}^{\infty}{\left(-1\right)^{-n}x\left(n\right)z^{-n}}=\sum_{-\infty}^{\infty}{x\left(n\right)\left(-z\right)^{-n}}=X\left(-z\right) ∑−∞∞(−1)nx(n)z−n=∑−∞∞(−1)−nx(n)z−n=∑−∞∞x(n)(−z)−n=X(−z) -
x(-n)的Z变换为:
∑ − ∞ ∞ x ( − n ) z − ( − n ) = ∑ − ∞ ∞ x ( − n ) ( z − 1 ) − n = X ( z − 1 ) = X ( 1 Z ) \sum_{-\infty}^{\infty}{x\left(-n\right)z^{-(-n)}}=\sum_{-\infty}^{\infty}{x\left(-n\right)\left(z^{-1}\right)^{-n}}=X\left(z^{-1}\right)=X\left(\frac{1}{Z}\right) ∑−∞∞x(−n)z−(−n)=∑−∞∞x(−n)(z−1)−n=X(z−1)=X(Z1)
x(2n)的Z变换为
∑ − ∞ ∞ x ( 2 n ) z − n \sum_{-\infty}^{\infty}{x\left(2n\right)z^{-n}} ∑−∞∞x(2n)z−n
令 k = 2 n k=2n k=2n
有 ∑ − ∞ ∞ x ( 2 n ) z − n = ∑ − ∞ ∞ x ( k ) z − k 2 \sum_{-\infty}^{\infty}{x\left(2n\right)z^{-n}}=\sum_{-\infty}^{\infty}{x\left(k\right)z^{-\frac{k}{2}}} ∑−∞∞x(2n)z−n=∑−∞∞x(k)z−2k
将 X ( z 1 2 ) = ∑ − ∞ ∞ x ( k ) z − k 2 X(z^{\frac{1}{2}})=\sum_{-\infty}^{\infty}{x\left(k\right)z^{-\frac{k}{2}}} X(z21)=∑−∞∞x(k)z−2k
X ( z − 1 2 ) = ∑ − ∞ ∞ x ( k ) ( − 1 ) k z − k 2 X(z^{-\frac{1}{2}})=\sum_{-\infty}^{\infty}{x\left(k\right)(-1)^{k}z^{-\frac{k}{2}}} X(z−21)=∑−∞∞x(k)(−1)kz−2k相加得
1 2 [ X ( z 1 2 ) + X ( − z 1 2 ) ] = ∑ − ∞ ∞ x ( k ) z − k 2 + ∑ − ∞ ∞ x ( k ) ( − 1 ) k z − k 2 = ∑ − ∞ ∞ x ( 2 n ) z − n \frac{1}{2}[X(z^\frac{1}{2})+X(-z^\frac{1}{2})]\\ =\sum_{-\infty}^{\infty}{x\left(k\right)z^{-\frac{k}{2}}}+\sum_{-\infty}^{\infty}{x\left(k\right)(-1)^{k}z^{-\frac{k}{2}}}\\=\sum_{-\infty}^{\infty}{x\left(2n\right)z^{-n}} 21[X(z21)+X(−z21)]=∑−∞∞x(k)z−2k+∑−∞∞x(k)(−1)kz−2k=∑−∞∞x(2n)z−n
-
3. 拉普拉斯旋转不变性证明
形式化描述什么是拉普拉斯算子,并证明拉普拉斯算子具有旋转不变性质
(二维平面内的旋转变换计算公式为 x ′ = x c o s θ − y s i n θ , y = x s i n θ + y c o s θ x'=xcosθ-ysinθ,y=xsinθ+ycosθ x′=xcosθ−ysinθ,y=xsinθ+ycosθ)
证明:

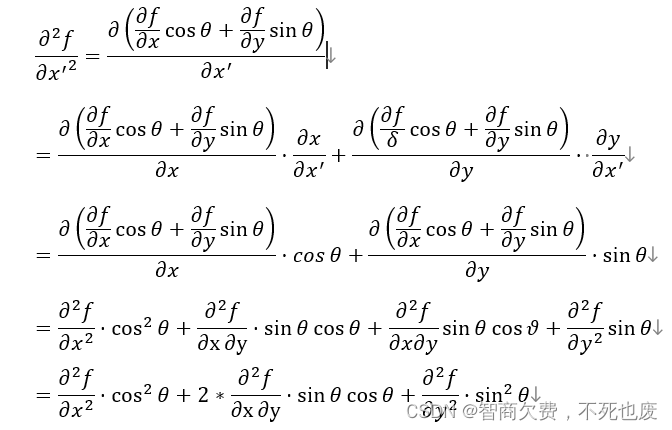
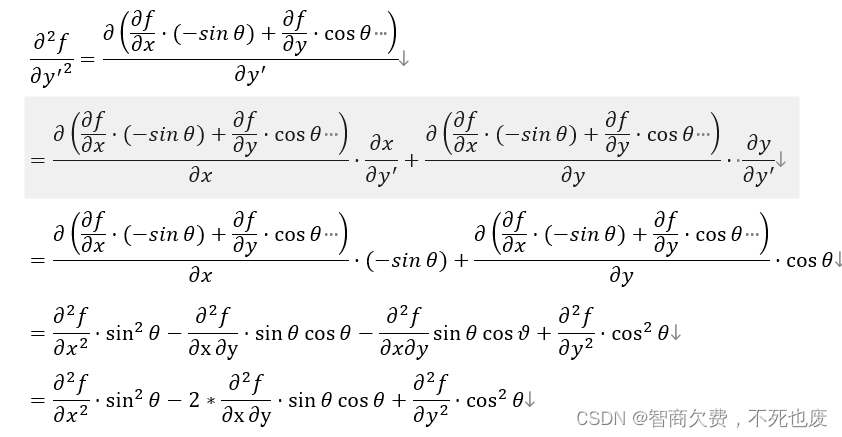

4.推导出随机数生成方程
假设我们有一个[0,1]上的均匀分布随机数发生器U(0,1), 请基于它构造指数分布的随机数发生器,推导出随机数生成方程。
若我们有一个标准正态分布的随机数发生器N(0,1),请推导出对数正态分布的随机数生成方程。
解: (1) 设U(0,1)可生成随机数 w ∈ [ 0 , 1 ] w\in [0,1] w∈[0,1],用它生成具有指数分布的随机数z,则其分布具有形式 F ( z ) = 1 − e − a z , z ≥ 0 F(z)=1-e^{-az},z\ge 0 F(z)=1−e−az,z≥0
令F(z)=w,解得: z = − 1 a l n [ 1 − U ( 0 , 1 ) ] z=-\frac{1}{a}ln[1-U(0,1)] z=−a1ln[1−U(0,1)]
(2) 设N(0,1)可生成随机数 w ∈ [ 0 , 1 ] w\in [0,1] w∈[0,1],用它生成具有正态分布的随机数z,则其分布具有形式 F ( z ) = ∫ 0 z 1 2 π b F(z)=\int_{0}^{z}\frac{1}{\sqrt{2\pi b}} F(z)=∫0z2πb1 e − [ l n ( v ) − a ] 2 2 b 2 d v e^{-\frac{[ln(v)-a]^{2}}{2b^{2}}}dv e−2b2[ln(v)−a]2dv
令F(z)=w,解得: z = e b w + a z=e^{bw+a} z=ebw+a
即 z = e b N ( 0 , 1 ) + a z=e^{bN(0,1)+a} z=ebN(0,1)+a
5. 快速小波变换分解与重建
在分析信号时小波分解与重建是一个重要的工具,离散 haar 小波是一种重要而简单J1/5 n=0.1的小波,它的尺度与小波向量分别为
- (1)现在假设我们有一个长度为8的信号f[1,-3,3,1,2,0,-2,1],利用快速哈尔小波变换进行三层的分解,计算各层的滤波器输出。
- (2)若利用哈尔小波对某个信号进行三层的分解的滤波器输出
W = [ W φ ( 1 , 0 ) , W φ ( 1 , 0 ) , W φ ( 2 , 0 ) , W φ ( 2 , 1 ) , W φ ( 3 , 0 ) , W φ ( 3 , 1 ) , W φ ( 3 , 2 ) , W φ ( 3 , 3 ) ] = [ 1 , 1 , − 1 , − 1 , 1 , 0 , 1 , 0 ] W=[W_{\varphi }(1,0),W_{\varphi }(1,0),W_{\varphi }(2,0),W_{\varphi }(2,1),W_{\varphi }(3,0),W_{\varphi }(3,1),W_{\varphi }(3,2),W_{\varphi }(3,3)]=[ 1,1,-1,-1,1,0,1,0] W=[Wφ(1,0),Wφ(1,0),Wφ(2,0),Wφ(2,1),Wφ(3,0),Wφ(3,1),Wφ(3,2),Wφ(3,3)]=[1,1,−1,−1,1,0,1,0],请计算重建原来的信号。
相关文章:

国科大图像处理2023速通期末——汇总2017-2019
国科大2023.12.28图像处理0854期末重点 图像处理 王伟强 作业 课件 资料 一、填空 一个阴极射线管它的输入与输出满足 s r 2 sr^{2} sr2,这将使得显示系统产生比希望的效果更暗的图像,此时伽马校正通常在信号进入显示器前被进行预处理,令p…...
oracle 9i10g编程艺术-读书笔记2
配置Statspack 安装Statspack需要用internal身份登陆,或者拥有SYSDBA(connect / as sysdba)权限的用户登陆。需要在本地安装或者通过telnet登陆到服务器。 select instance_name,host_name,version,startup_time from v$instance;检查数据文件路径及磁盘空间&…...

PACC:数据中心网络的主动 CNP 生成方案
PACC:数据中心网络的主动 CNP 生成方案 文章目录 PACC:数据中心网络的主动 CNP 生成方案PACC算法CNP数据结构PACC参数仿真结果参考文献 PACC算法 CNP数据结构 PACC参数 仿真结果 PACC Hadoop Load0.2 的情况: PACC Hadoop Load0.4 的情况&a…...

我最喜欢的趣味几何书-读书笔记
我最喜欢的趣味几何书-读书笔记 1、利用阴影的长度来测量 公元前6世纪,古希腊哲学家泰勒思为了测量金字塔,想到了这样的方法:选择了一个特殊的时间,在那个时间,他自身的影子长度刚好跟他的身高相等。此时,…...
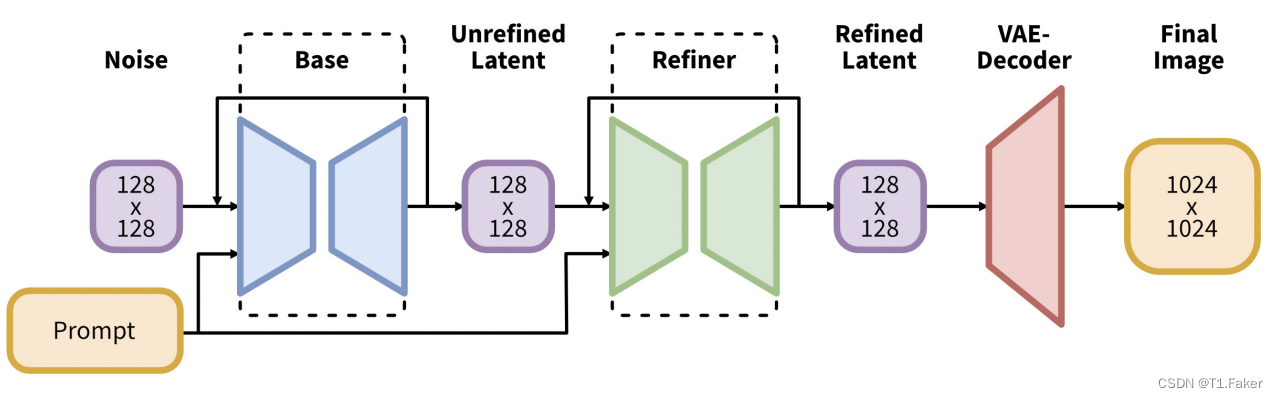
Stable Diffusion模型概述
Stable Diffusion 1. Stable Diffusion能做什么?2. 扩散模型2.1 正向扩散2.2 反向扩散 3. 训练如何进行3.1 反向扩散3.2 Stable Diffusion模型3.3 潜在扩散模型3.4 变分自动编码器3.5 图像分辨率3.6 图像放大 4. 为什么潜在空间是可能的?4.1 在潜在空间中…...

二叉树详解(深度优先遍历、前序,中序,后序、广度优先遍历、二叉树所有节点的个数、叶节点的个数)
目录 一、树概念及结构(了解) 1.1树的概念 1.2树的表示 二、二叉树概念及结构 2.1概念 2.2现实中的二叉树: 2.3数据结构中的二叉树: 2.4特殊的二叉树: 2.5 二叉树的存储结构 2.51 顺序存储: 2.5.2 链式存储&…...
C++日期类的实现
前言:在类和对象比较熟悉的情况下,我们我们就可以开始制作日期表了,实现日期类所包含的知识点有构造函数,析构函数,函数重载,拷贝构造函数,运算符重载,const成员函数 1.日期类的加减…...

B+树的插入删除
操作 插入 case2的原理,非叶子节点永远和最右边的最左边的节点的值相等。 case3:的基本原理 非叶子节点都是索引节点 底层的数据分裂之后 相当于向上方插入一个新的索引(你可以认为非叶子节点都是索引),反正第二层插入160 都要分裂,然后也需要再插入(因为索引部分不需要重…...

c# Avalonia 绘图
在Avalonia UI框架中,绘图主要通过使用DrawingContext类来实现。DrawingContext提供了一系列的绘图API,可以用来绘制线条、形状、图像以及文本等内容。以下是一个简单的示例,说明如何在Avalonia中进行基础的图形绘制 <!-- MainWindow.axa…...

springboot 双数据源配置
1:pom <!--SpringBoot启动依赖--><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-web</artifactId></dependency><dependency><groupId>org.springframework.boot</group…...
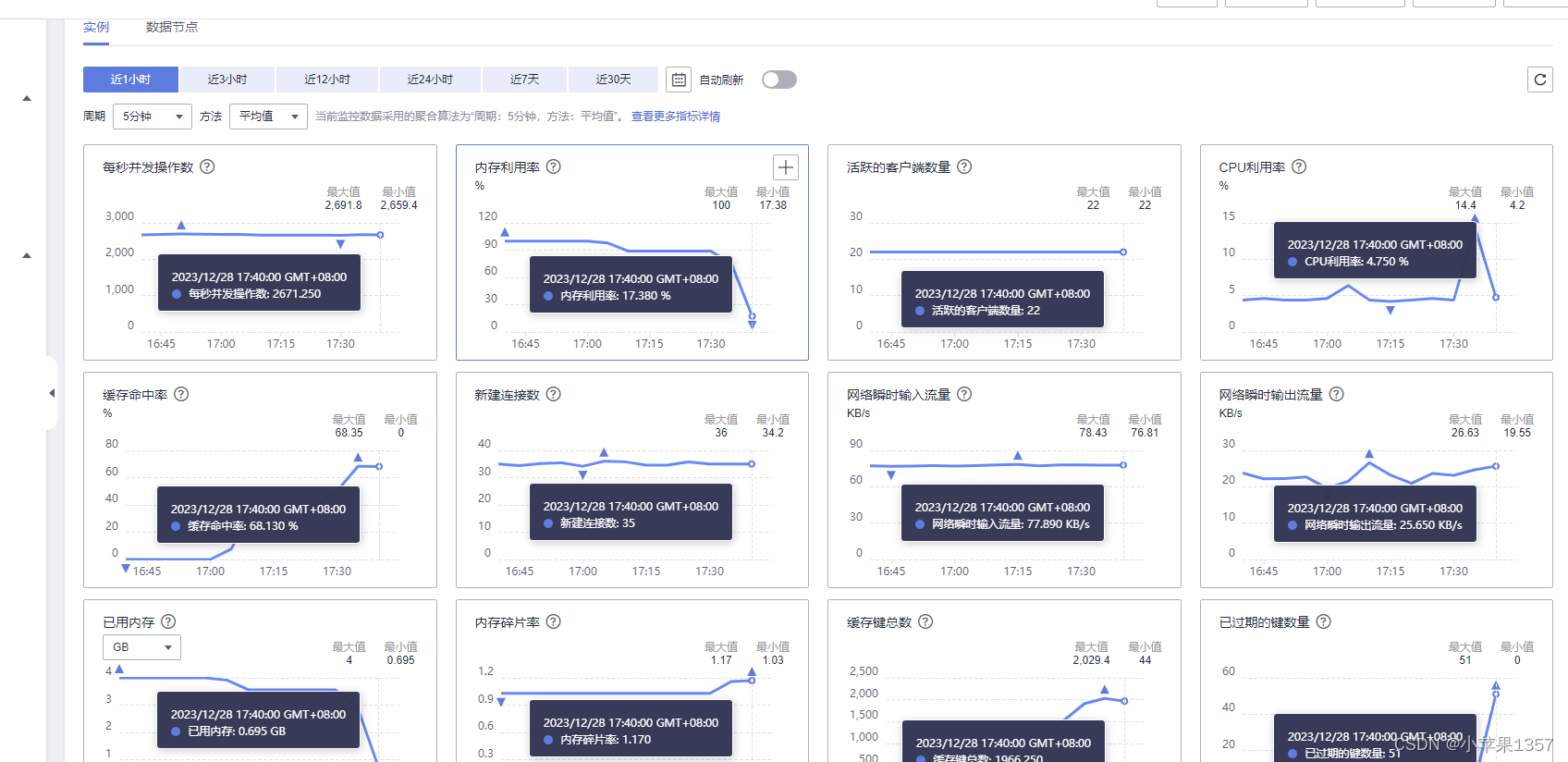
Redis内存使用率高,内存不足问题排查和解决
问题现象 表面现象是系统登录突然失效,排查原因发现,使用redis查询用户信息异常,从而定位到redis问题 if (PassWord.equals(dbPassWord)) {map.put("rtn", 1);map.put("value", validUser);session.setAttribute("…...
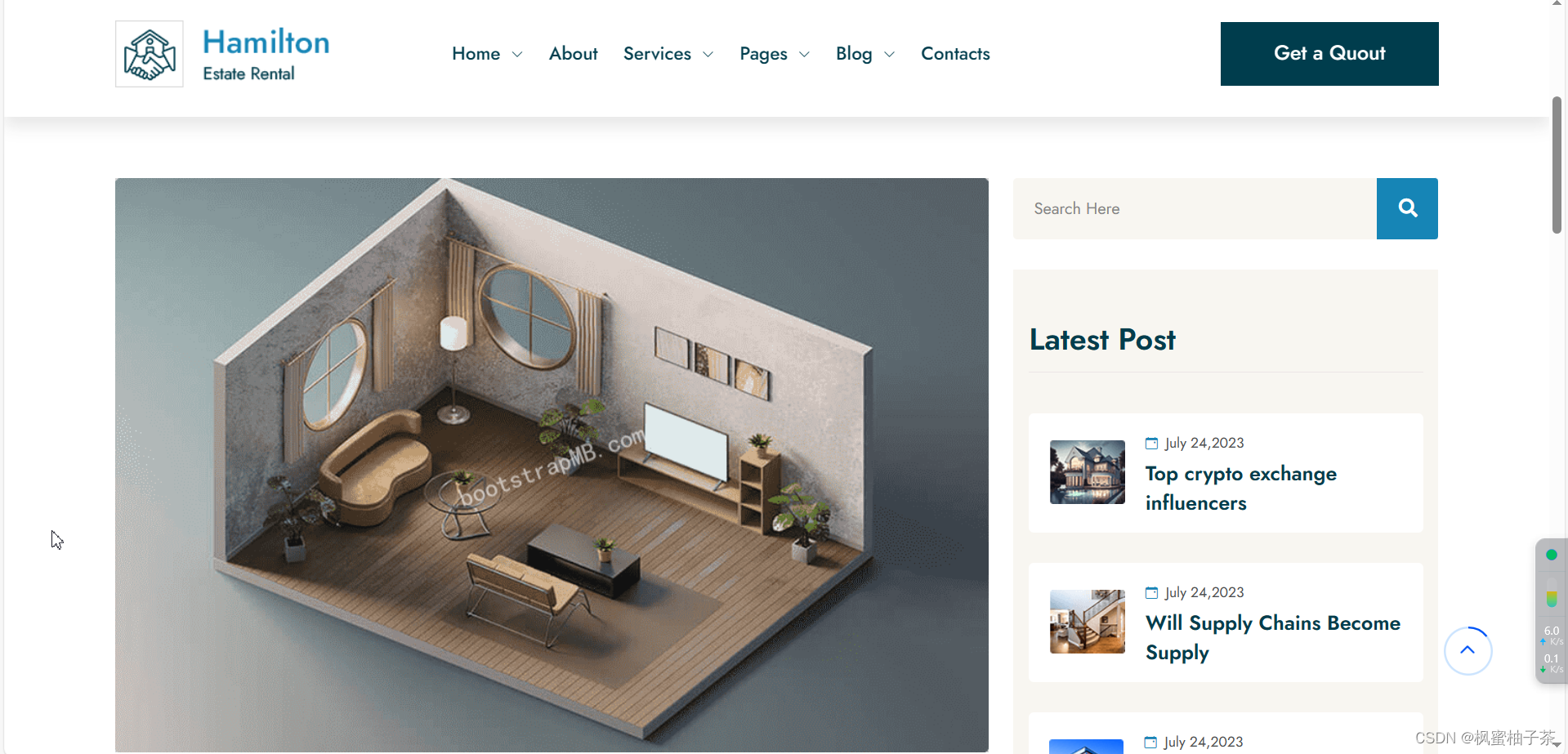
bootstrap5开发房地产代理公司Hamilton前端页面
一、需求分析 房地产代理网站是指专门为房地产行业提供服务的在线平台。这些网站的主要功能是连接房地产中介机构、房产开发商和潜在的买家或租户,以促成买卖或租赁房产的交易。以下是一些常见的房地产代理网站的功能: 房源发布:房地产代理网…...
2024年Mac专用投屏工具AirServer 7 .27 for Mac中文版
AirServer 7 .27 for Mac中文免费激活版是一款Mac专用投屏工具,能够通过本地网络将音频、照片、视频以及支持AirPlay功能的第三方App,从 iOS 设备无线传送到 Mac 电脑的屏幕上,把Mac变成一个AirPlay终端的实用工具。 目前最新的AirServer 7.2…...

关于MySql字段类型的实践总结
当字段为数值类型时应使用无符号UNSIGNED修饰 ALTER TABLE infoMODIFY COLUMN user_id int UNSIGNED NOT NULL; 当字段为varchar类型时应注意是否选择合适的字符集 例如存储一些范围值,数字英文字符时(IP、生日、客户端标识等或以“,”分隔的数据&…...
UG NX二次开发(C#)-Ufun和NXOpen混合编程
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 1、前言2、Ufun函数3、 NXOpen4、混合编程实现1、前言 在UG NX二次开发过程中,采用Ufun功能比较简单,能用比较少的代码实现我们需要的功能,但是ufun函数的功能不是很强大,尤其随着UG NX的版本…...
【Spark精讲】一文讲透Spark RDD
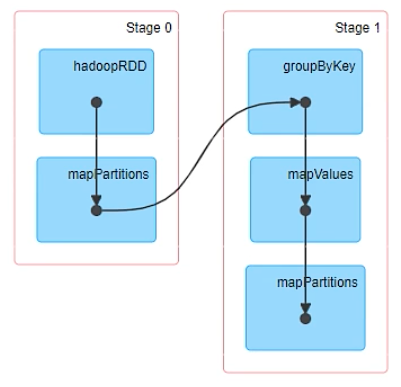
MapReduce的缺陷 MR虽然在编程接口的种类和丰富程度上已经比较完善了,但这些系统普遍都缺乏操作分布式内存的接口抽象,导致很多应用在性能上非常低效 。 这些应用的共同特点是需要在多个并行操 作之间重用工作数据集 ,典型的场景就是机器学习…...

如在MT9040、IDT82V3001A 等锁相环上电后或输入参考频率改变后必须复位锁相环。
锁相环是一种反馈控制系统,它能够将输出信号的相位锁定到输入参考信号的相位上。在实际应用中,如MT9040、IDT82V3001A等PLL集成电路在上电后或者当输入参考频率发生变化后通常需要复位的原因涉及到几个方面: 1、初始化状态: 当PLL电路上电时,其内部的各个组件可能…...

构建安全的SSH服务体系
某公司的电子商务站点由专门的网站管理员进行配置和维护,并需要随时从Internet进行远程管理,考虑到易用性和灵活性,在Web服务器上启用OpenSSH服务,同时基于安全性考虑,需要对 SSH登录进行严格的控制,如图10…...

wpf ComboBox绑定数据及变更事件
定义ComboBox,以及SelectionChanged事件 <ComboBox x:Name"cmb_radius" Height"30" Width"65" FontSize"15" DisplayMemberPath"Value" SelectedValuePath"Key" HorizontalAlignment"Center&…...

SQL BETWEEN 操作符
BETWEEN 操作符选取介于两个值之间的数据范围内的值。这些值可以是数值、文本或者日期。 SQL BETWEEN 语法 SELECT column1, column2, ... FROM table_name WHERE column BETWEEN value1 AND value2; 参数说明: column1, column2, ...:要选择的字段名…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...
32单片机——基本定时器
STM32F103有众多的定时器,其中包括2个基本定时器(TIM6和TIM7)、4个通用定时器(TIM2~TIM5)、2个高级控制定时器(TIM1和TIM8),这些定时器彼此完全独立,不共享任何资源 1、定…...

react-pdf(pdfjs-dist)如何兼容老浏览器(chrome 49)
之前都是使用react-pdf来渲染pdf文件,这次有个需求是要兼容xp环境,xp上chrome最高支持到49,虽然说iframe或者embed都可以实现预览pdf,但为了后续的定制化需求,还是需要使用js库来渲染。 chrome 49测试环境 能用的测试…...

VUE3 ref 和 useTemplateRef
使用ref来绑定和获取 页面 <headerNav ref"headerNavRef"></headerNav><div click"showRef" ref"buttonRef">refbutton</div>使用ref方法const后面的命名需要跟页面的ref值一样 const buttonRef ref(buttonRef) cons…...

旋量理论:刚体运动的几何描述与机器人应用
旋量理论为描述刚体在三维空间中的运动提供了强大而优雅的数学框架。与传统的欧拉角或方向余弦矩阵相比,旋量理论通过螺旋运动的概念统一了旋转和平移,在机器人学、计算机图形学和多体动力学领域具有显著优势。这种描述不仅几何直观,而且计算…...

智慧城市项目总体建设方案(Word700页+)
1 背景、现状和必要性 1.1 背景 1.1.1 立项背景情况 1.1.2 立项依据 1.2 现状 1.2.1 党建体系运行现状 1.2.2 政务体系运行现状 1.2.3 社会治理运行现状 1.2.4 安全监管体系现状 1.2.5 环保体系运行现状 1.2.6 城建体系运行现状 1.2.7 社区体系运行现状 1.2.8 园区…...
