代码随想Day55 | 392.判断子序列、115.不同的子序列

392.判断子序列 

第一种思路是双指针，详细代码如下：

class Solution {
public:bool isSubsequence(string s, string t) {//双指针if(s.empty()&&t.empty()) return true;int i=0,j=0;while(i<t.size()){if(s[j]==t[i]) j++;if(j==s.size()) return true;i++;}return false;}
};

按照动态规划的思路：

这道题和最长公共子序列(不连续)几乎相同，找的是两个字符的最长公共部分，但是这道题是s已经是子序列了，所以不相等的时候s序列不需要进行删除，只需要删除s的元素，如果最长公共部分长度和s的长度相同，则返回true，否则返回false，不再详细进行动态规划的分析。

详细代码如下：

class Solution {
public:bool isSubsequence(string s, string t) {if(s.empty()&&t.empty()) return true;vector<vector<int>>dp(s.size()+1,vector<int>(t.size()+1,0));for(int i=1;i<=s.size();i++){for(int j=1;j<=t.size();j++){if(s[i-1]==t[j-1]) dp[i][j]=dp[i-1][j-1]+1;else dp[i][j]=dp[i][j-1];}}if(dp[s.size()][t.size()]==s.size()) return true;else return false;}
};

115.不同的子序列 

这道题的需要延续判断子序列的思路：

dp[i][j]:以s[i-1]结尾的t[j-1]结尾的子序列个数；

递推：

这一类问题，基本是要分析两种情况

• s[i - 1] 与 t[j - 1]相等
• s[i - 1] 与 t[j - 1] 不相等

当s[i - 1] 与 t[j - 1]相等时，dp[i][j]可以有两部分组成。一部分是用s[i - 1]来匹配，那么个数为dp[i - 1][j - 1]。即不需要考虑当前s子串和t子串的最后一位字母，所以只需要 dp[i-1][j-1]。一部分是不用s[i - 1]来匹配，个数为dp[i - 1][j]。

初始化：

从递推公式dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; 和 dp[i][j] = dp[i - 1][j]; 中可以看出dp[i][j] 是从上方和左上方推导而来，如图：，那么 dp[i][0] 和dp[0][j]是一定要初始化的。

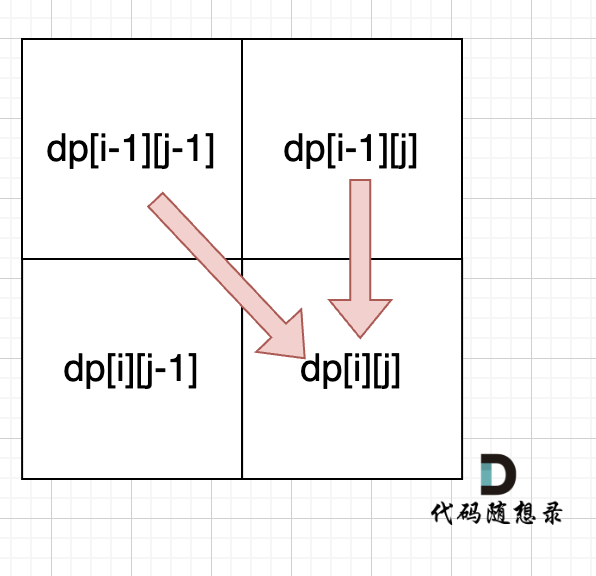
每次当初始化的时候，都要回顾一下dp[i][j]的定义，不要凭感觉初始化。

dp[i][0]表示什么呢？

dp[i][0] 表示：以i-1为结尾的s可以随便删除元素，出现空字符串的个数。

那么dp[i][0]一定都是1，因为也就是把以i-1为结尾的s，删除所有元素，出现空字符串的个数就是1。

再来看dp[0][j]，dp[0][j]：空字符串s可以随便删除元素，出现以j-1为结尾的字符串t的个数。

那么dp[0][j]一定都是0，s如论如何也变成不了t。

最后就要看一个特殊位置了，即：dp[0][0] 应该是多少。

dp[0][0]应该是1，空字符串s，可以删除0个元素，变成空字符串t。

详细代码如下：

class Solution {
public:int numDistinct(string s, string t) {vector<vector<uint64_t>>dp(s.size()+1,vector<uint64_t>(t.size()+1,0));for(int i=0;i<=s.size();i++) dp[i][0]=1;for(int i=1;i<=s.size();i++){for(int j=1;j<=t.size();j++){if(s[i-1]==t[j-1]) dp[i][j]=dp[i-1][j-1]+dp[i-1][j]; //使用s[i-1]和不else dp[i][j]=dp[i-1][j];}}return dp[s.size()][t.size()];}
};