力扣:509. 斐波那契数(动态规划,附带递归版本) 详细讲解动态规划的思路
题目:
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1
F(n) = F(n - 1) + F(n - 2),其中 n > 1
给定 n ,请计算 F(n) 。
示例 1:
输入:n = 2
输出:1
解释:F(2) = F(1) + F(0) = 1 + 0 = 1
示例 2:
输入:n = 3
输出:2
解释:F(3) = F(2) + F(1) = 1 + 1 = 2
示例 3:
输入:n = 4
输出:3
解释:F(4) = F(3) + F(2) = 2 + 1 = 3
提示:
0 <= n <= 30
思路:
本题很简单,但很适合用来做动态规划(和递归)的入门题,本篇文章主要讲解一下动态规划的思路。
动态规划
动规五部曲:
这里我们要用一个一维dp数组来保存递归的结果
- 确定dp数组以及下标的含义
dp[i]的定义为:第i个数的斐波那契数值是dp[i]
- 确定递推公式
为什么这是一道非常简单的入门题目呢?
因为题目已经把递推公式直接给我们了:状态转移方程 dp[i] = dp[i - 1] + dp[i - 2];
- dp数组如何初始化
题目中把如何初始化也直接给我们了,如下:
dp[0] = 0dp[1] = 1
- 确定遍历顺序
从递归公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出,dp[i]是依赖 dp[i - 1] 和 dp[i - 2],那么遍历的顺序一定是从前到后遍历的
- 举例推导dp数组
按照这个递推公式dp[i] = dp[i - 1] + dp[i - 2],我们来推导一下,当N为10的时候,dp数组应该是如下的数列:
0 1 1 2 3 5 8 13 21 34 55
如果代码写出来,发现结果不对,就把dp数组打印出来看看和我们推导的数列是不是一致的。
以上就是动态规划五部曲 这在之后将贯穿所有动态规划类的题目
完整代码和复杂度分析:
动态规划版本1(定义dp数组):
class Solution:def fib(self, n: int) -> int:# 排除 Corner Caseif n == 0:return 0# 创建 dp table dp = [0] * (n + 1)# 初始化 dp 数组dp[0] = 0dp[1] = 1# 遍历顺序: 由前向后。因为后面要用到前面的状态for i in range(2, n + 1):# 确定递归公式/状态转移公式dp[i] = dp[i - 1] + dp[i - 2]# 返回答案return dp[n]
- 时间复杂度:O(n)
- 空间复杂度:O(n)
动态规划版本2(不自定义dp数组,仅使用3个变量来维护dp数组):
class Solution:def fib(self, n: int) -> int:if n <= 1:return ndp = [0, 1]for i in range(2, n + 1):total = dp[0] + dp[1]dp[0] = dp[1]dp[1] = totalreturn dp[1]
- 时间复杂度:O(n)
- 空间复杂度:O(1)
递归版本:
class Solution:def fib(self, n: int) -> int:if n < 2:return nreturn self.fib(n - 1) + self.fib(n - 2)
- 时间复杂度:O(2^n)
- 空间复杂度:O(n)
相关文章:
 详细讲解动态规划的思路)
力扣:509. 斐波那契数(动态规划,附带递归版本) 详细讲解动态规划的思路
题目: 斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是: F(0) 0,F(1) 1 F(n) F(n - 1) F(n - 2),其中…...

Python3,压箱底的代码片段,提升工作效率稳稳的。
压箱底代码存活 1、引言2、代码实例2.1 操作存储服务2.1.1 Redis操作2.1.2 MongoDB操作2.1.3 MySQL操作 2.2 异步操作2.3 多线程 3、总结 1、引言 小屌丝:鱼哥,这年底了,得不得分享一点压箱底的东西啊 小鱼:… 压箱底的东西&…...

Flowable-升级为7.0.0.M2-第三节
目录 启动项目添加虚拟机参数启动成功 启动项目 添加虚拟机参数 java.base/java.langALL-UNNAMED --add-opens java.base/java.mathALL-UNNAMED --add-opens java.base/java.util.concurrentALL-UNNAMED --add-opens java.base/java.netALL-UNNAMED --add-opens java.base/ja…...

JavaWeb——前端之AjaxVue
6. 前后端交互 6.1 Ajax(原生的) 概念: Asynchronous JavaScript And XML(异步的JavaScript和XML) 作用: 数据交互:通过Ajax可以给服务器发送请求,并获取服务器响应的数据异步交…...
在 Android 手机上从SD 卡恢复数据的 6 个有效应用程序
如果您有 Android 设备,您可能会将个人和专业的重要文件保存在设备的 SD 卡上。这些文件包括照片、视频、文档和各种其他类型的文件。您绝对不想丢失这些文件,但当您的 SD 卡损坏时,数据丢失是不可避免的。 幸运的是,您不需要这样…...

uni-app/vue封装etc车牌照输入,获取键盘按键键值
先看下效果如下: 动态图如下 uniapp的keyup获取不到keyCode和compositionstart,compositionend,所以需要监听input节点的keyup事件, 思路以及代码如下: 1.将每一个字符用文本框输入,代码如下 <view …...

iostat获取IO延迟单位从ms调整us的方案
iostat命令统计的磁盘I/O延迟通常是以毫秒(ms)为单位,例如在输出中的await字段表示的是平均服务时间,包括等待时间和处理时间,这个值就是以毫秒为单位。 然而,要获取更精确到微秒级别(us&#x…...

K8s 源码剖析及debug实战之 Kube-Scheduler(四):预选算法详解
文章目录 0. 引言1. 回顾2. podFitsOnNode 为什么执行两次预选3. 预选算法有哪些4. 参考 0. 引言 欢迎关注本专栏,本专栏主要从 K8s 源码出发,深入理解 K8s 一些组件底层的代码逻辑,同时借助 debug Minikube 来进一步了解 K8s 底层的代码运行…...
ES6之解构赋值详解
✨ 专栏介绍 在现代Web开发中,JavaScript已经成为了不可或缺的一部分。它不仅可以为网页增加交互性和动态性,还可以在后端开发中使用Node.js构建高效的服务器端应用程序。作为一种灵活且易学的脚本语言,JavaScript具有广泛的应用场景&#x…...
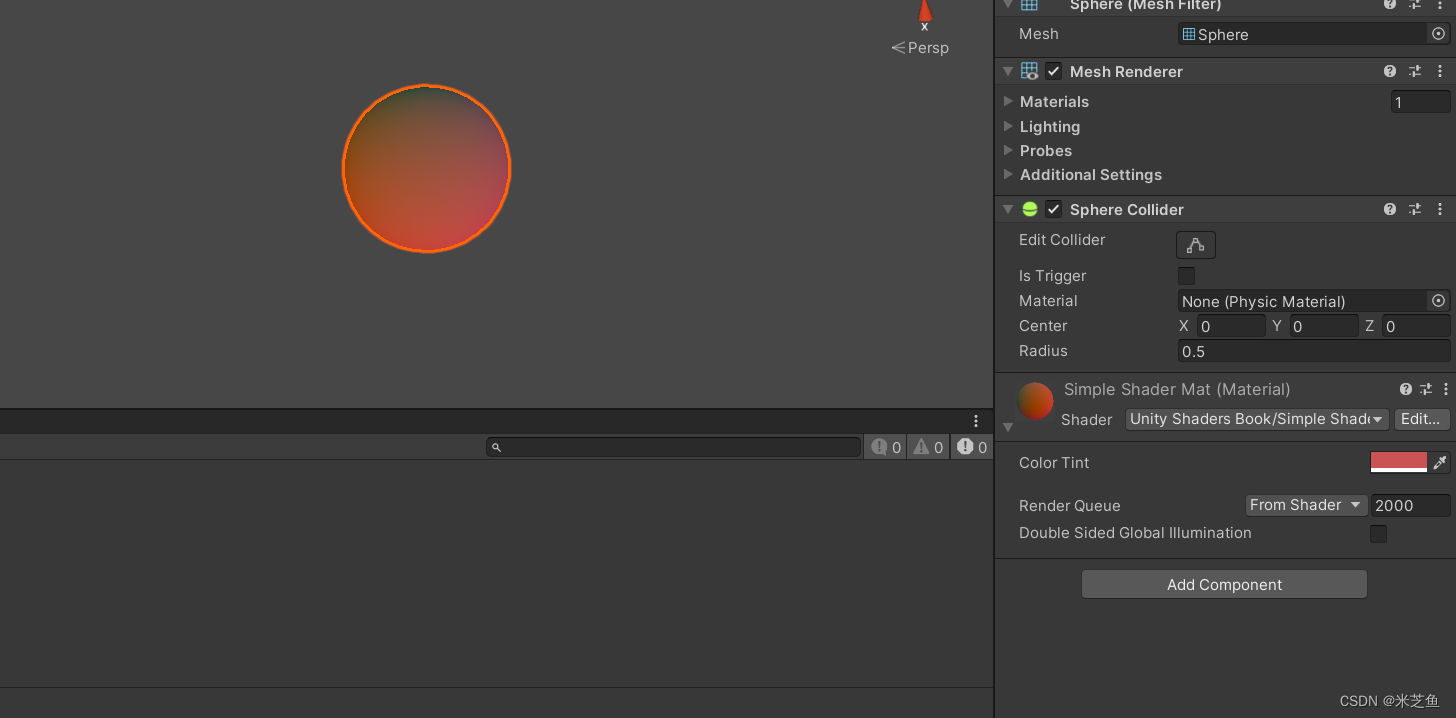
UntiyShader(五)属性、内置文件和变量
目录 一、如何使用属性 例子 ShaderLab中的属性的类型和Cg中的变量的类型之间的匹配关系 二、Unity提供的内置文件和变量 内置的包含文件 内置的变量 一、如何使用属性 在一开始我们提到过,材质和UnityShader之间有着密切的练习,我们可以通过材质面…...

Pytorch简介
1.1 Pytorch的历史 PyTorch是一个由Facebook的人工智能研究团队开发的开源深度学习框架。在2016年发布后,PyTorch很快就因其易用性、灵活性和强大的功能而在科研社区中广受欢迎。下面我们将详细介绍PyTorch的发展历程。 在2016年,Facebook的AI研究团队…...
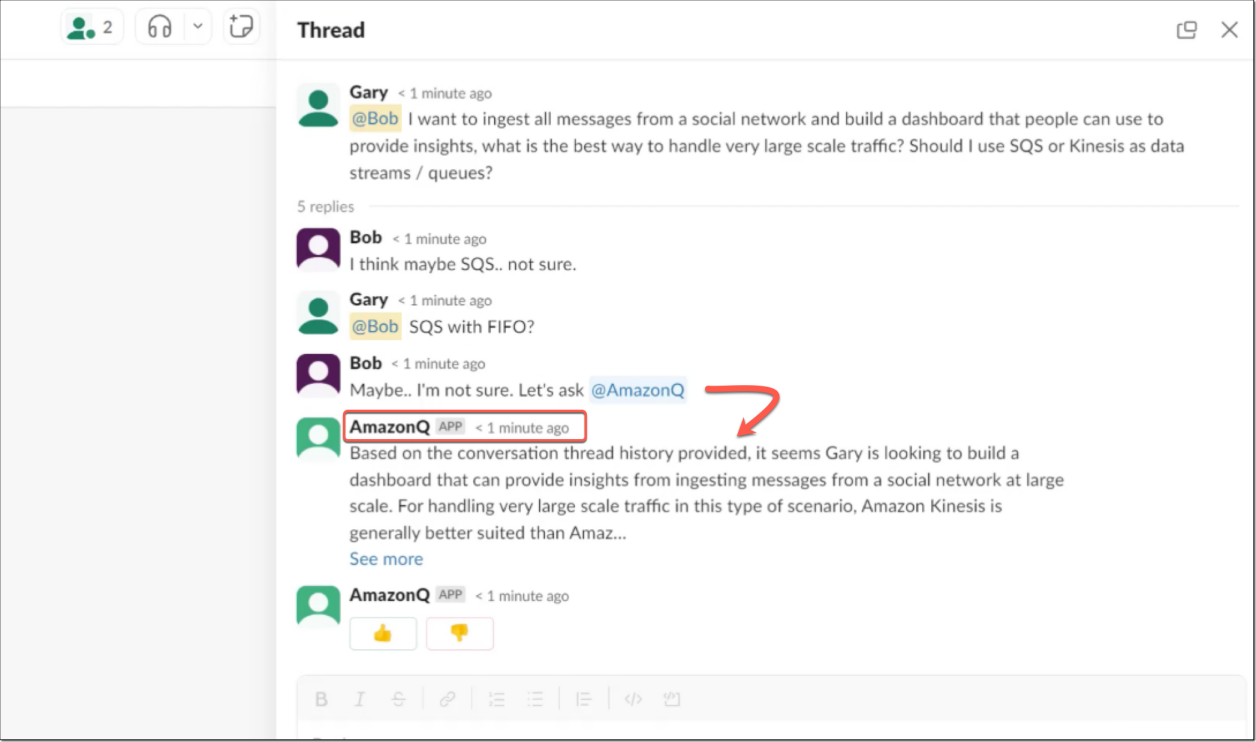
亚马逊云科技Amazon Q,一款基于生成式人工智能的新型助手
近日,亚马逊云科技宣布推出Amazon Q,这是一款基于生成式人工智能(AI)的新型助手,专为辅助工作而设计,可以根据您的业务量身定制。通过连接到公司的信息存储库、代码、数据和企业系统,可以使用Am…...
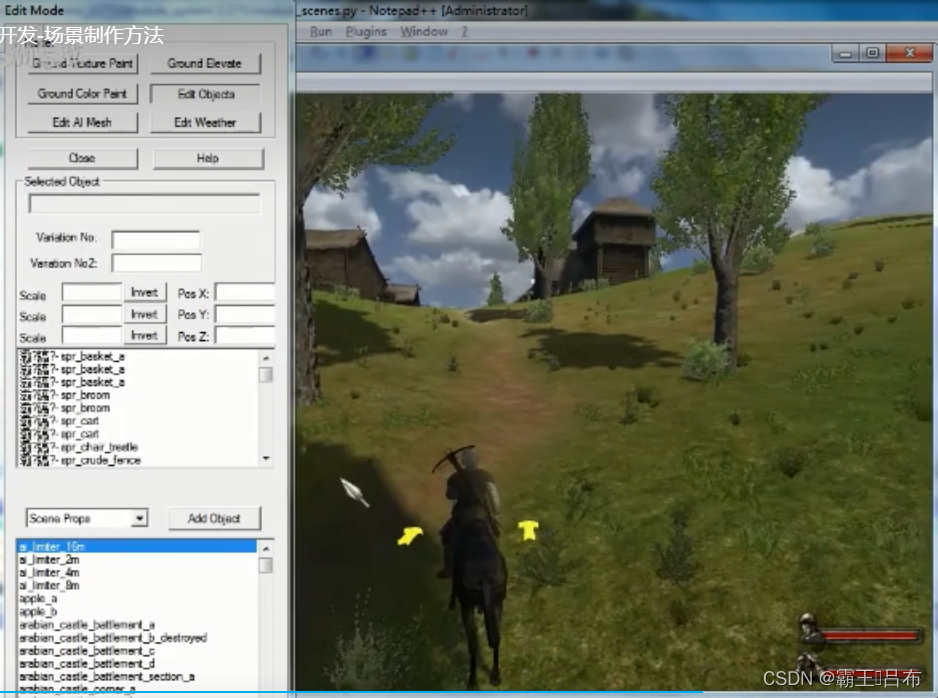
骑砍战团MOD开发(29)-module_scenes.py游戏场景
骑砍1战团mod开发-场景制作方法_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1Cw411N7G4/ 一.骑砍游戏场景 骑砍战团中进入城堡,乡村,战斗地图都被定义为场景,由module_scenes.py进行管理。 scene(游戏场景) 天空盒(Skyboxes.py) 地形(terrain code) 场景物(scene_…...
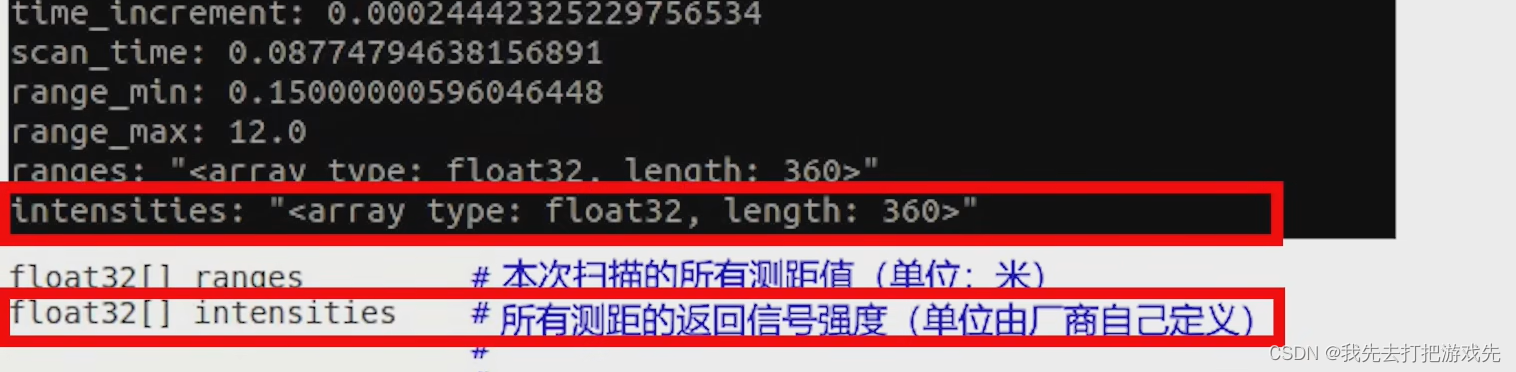
ROS学习记录:ROS系统中的激光雷达消息包的数据格式
一、在工作空间中输入source ./devel/setup.bash 二、输入roslaunch wpr_simulation wpb_simple.launch打开机器人仿真环境 三、机器人仿真环境打开成功 四、给机器人围上一圈障碍物 五、再打开一个工作空间终端 六、输入roslaunch wpr_simulation wpb_rviz.launch打开RViz 七、…...
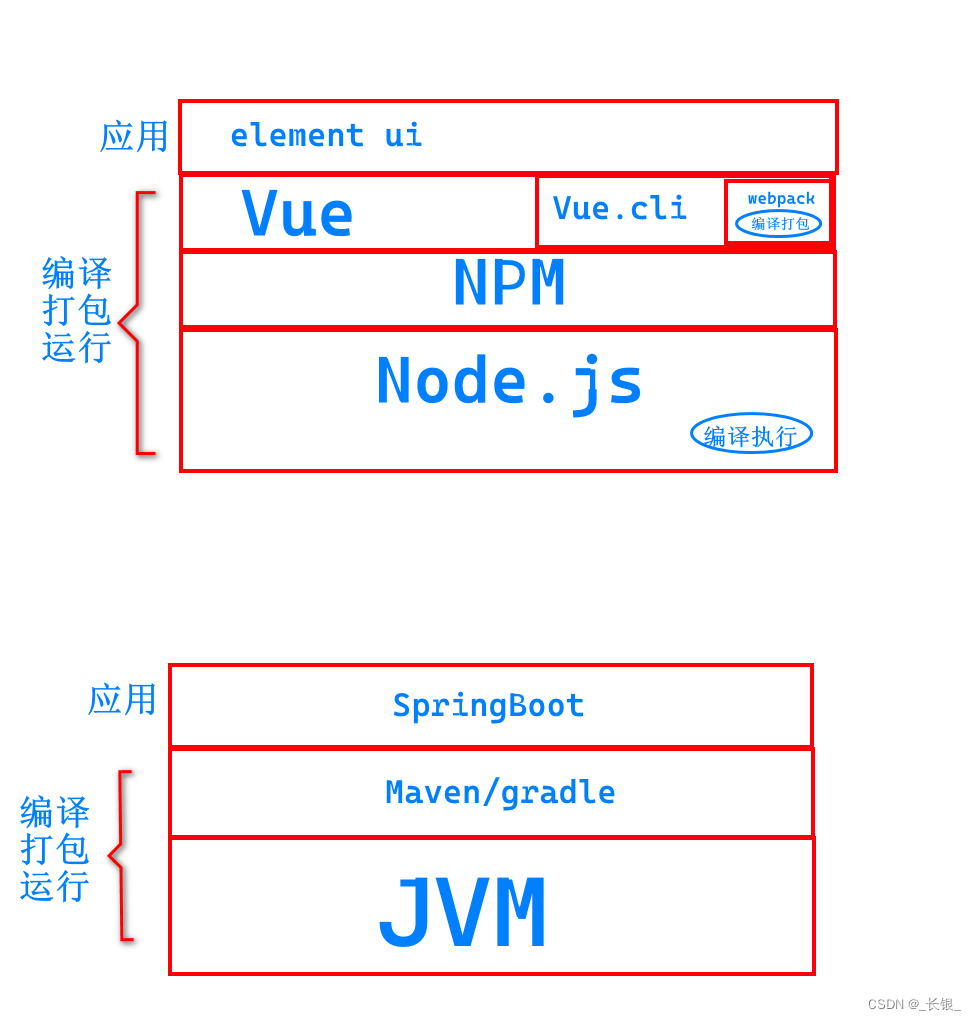
Vue.js和Node.js的关系--类比Java系列
首先我们看一张图 这里我们类比了Java的jvm和JavaScript的node.js。 可以看到,node.js是基础,提供了基础的编译执行的能力。vue,js是实际上定义了一种他自己的代码格式,以加速开发。...

我的笔记本电脑死机问题折腾记录
两年前,买了一台笔记本电脑。直到今年4月份,不到两年的时间,便出现了花屏的情况,然后就到官方售后去维修,换屏。然后在6月份,屏幕问题再次出现,又去售后维修。 经过两次维修,笔记本…...

uniApp中uView组件库的丰富布局方法
目录 基本使用 #分栏间隔 #混合布局 #分栏偏移 #对齐方式 API #Row Props #Col Props #Row Events #Col Events UniApp的uView组件库是一个丰富的UI组件库,提供了各种常用的UI组件和布局方法,帮助开发者快速构建美观、灵活的界面。下面给你写一…...
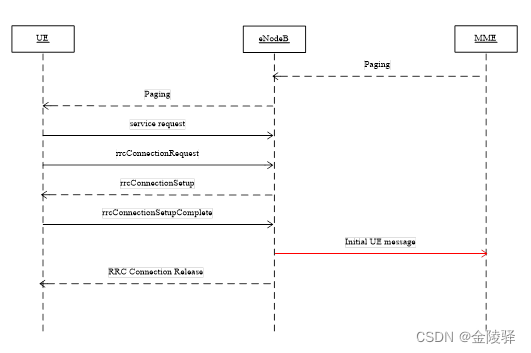
TDD-LTE 寻呼流程
目录 1. 寻呼成功流程 1.1 空闲态寻呼 1.2 连接态寻呼 2. 寻呼失败流程 2.1 Paging消息不可达 2.2 RRC建立失败 2.3 eNodeB未上发Initial UE message或达到超时 1. 寻呼成功流程 1.1 空闲态寻呼 寻呼成功:MME发起寻呼(S1 接口发送Paing 消息&…...
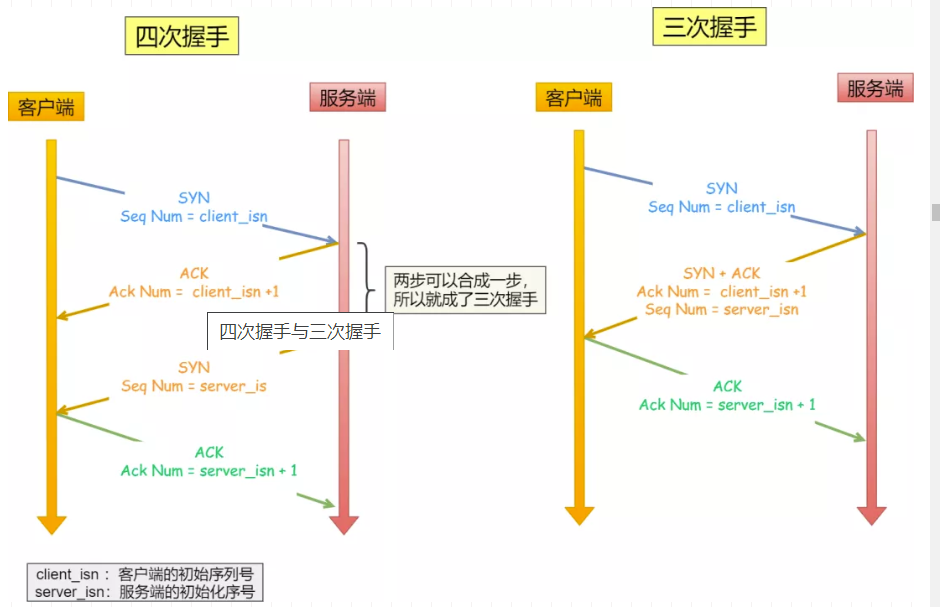
TCP中的三次握手和四次挥手
TCP中的连接和断开可以说是在面试中经常被问到的问题之一,正好有空就总结一下,首先回顾一下TCP的相关知识点 1. TCP的基础知识 1.1 TCP的基本概念 我们知道TCP是运输层的面向连接的可靠的传输协议。面向连接的,指的就是在两个进程发送数据…...
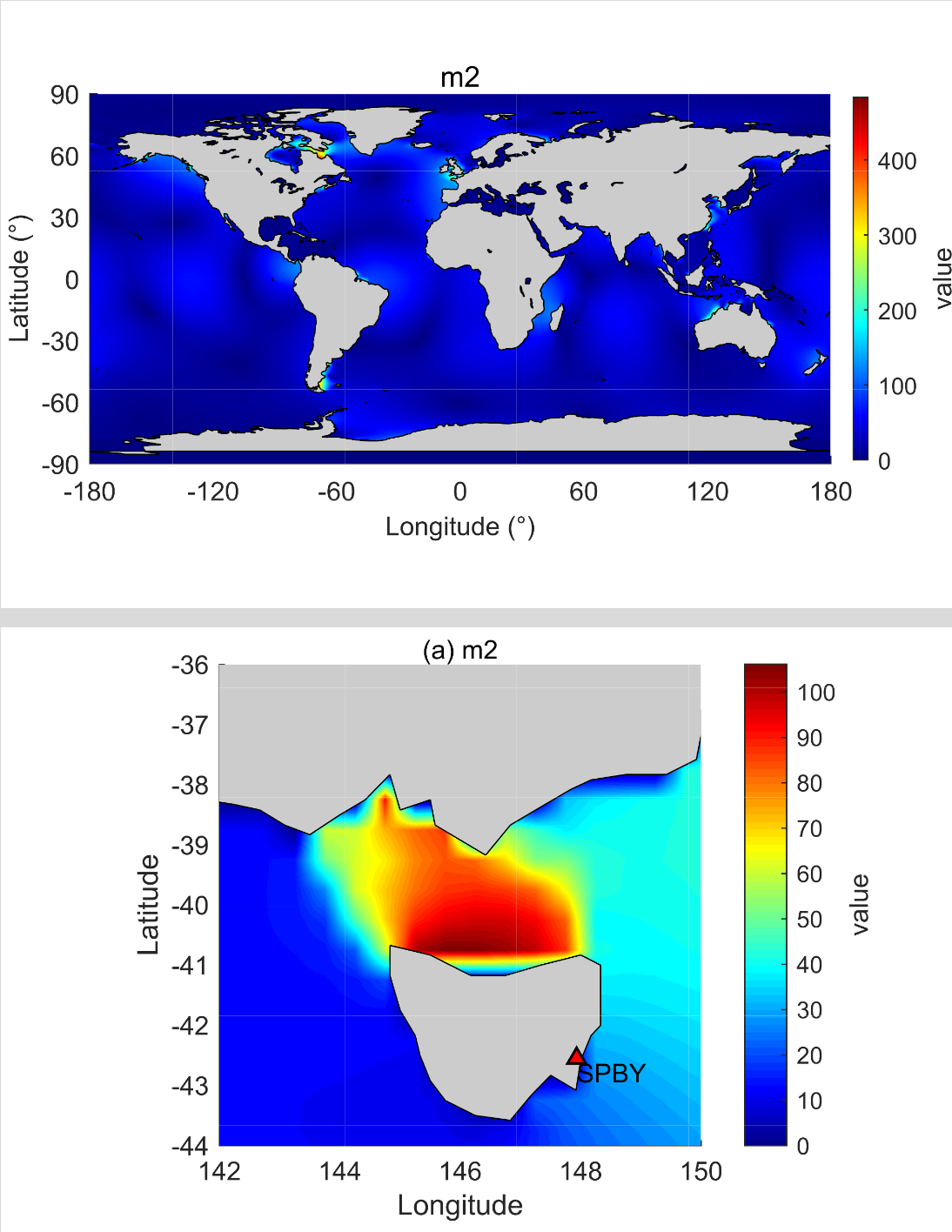
NAO.99b海潮模型的详解教程
NAO.99b模型是由日本国家天文台开发的全球潮汐模式,基于二维非线性浅水方程。该模型具有较高的分辨率,网格间距为0.50.5,网格数为720360,覆盖的经度范围为0.25~359.75E,纬度范围为89.75S~89.75N…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...
