【数据结构】图论与并查集
一、并查集
1.原理
- 简单的讲并查集,就是
查询两个个元素,是否在一个集合当中,这里的集合用树的形式进行表示。 - 并查集的本质就是
森林, 即多棵树。
我们再来简单的举个例子:
- 假设此时的你是大一新生,刚进入大学,肯定是先找到宿舍在哪里,然后跟寝室里面的舍友互相认识一下,先形成一个小团体。
- 假设,宿舍总共6个人,也就是6个人的集合。几乎所有的大学生都是这样先跟周围的人进行联系起来的。
- 然后辅导员召集班会,这时的你欣然前往,并在讲台上自信的介绍自己,然后吸引或者主动又认识了一群人。这时你或许又跟其它的人进行了关联,或成为了好友,或成为了恋人……
下面我们用如上例子进行展开讨论:
- 宿舍六人,即六个人,如何判断两个人在同一个集合? 如何进行实现?
- 先来解决第一个问题,六个人,选出一个宿舍长,只要两个人的宿舍长是一样的,即可判断两个人在一个集合。
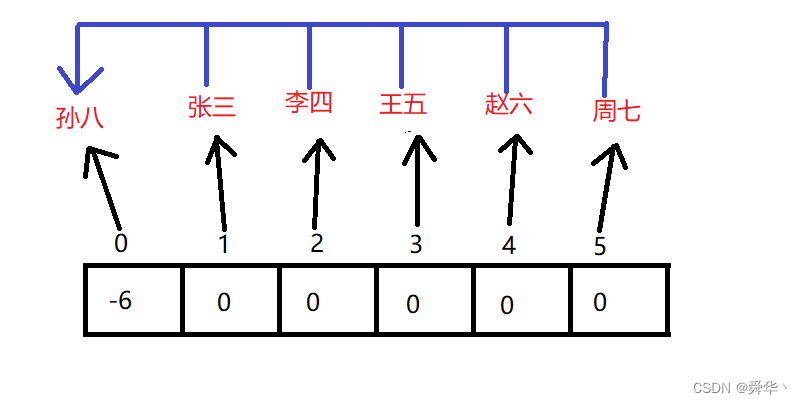
- 再来解决第二个问题,既然宿舍长有了,我们都与这个宿舍长产生关联即可,即用树的形式进行表示,至于如何表示,我们可以用双亲表示法进行表示,即每个人记住其宿舍长的名字即可。更为形象的我们可以用下图进行表示:
- 更进一步,如何用计算机存储这种结构呢?我们只需对每个人名生成一个下标连续,用计算机进行存储即可。用下图进行直观的理解:
- 对这张图我们再说明一点,除0下标以外的其他位置存放的是指向代表孙八的下标,这个0处下标存的是集合的所有元素的个数,且存放的是负数形式,这样存有一个好处,我们可以由这个并查集中有多少负数,从而判断这个并查集中有多少个集合。
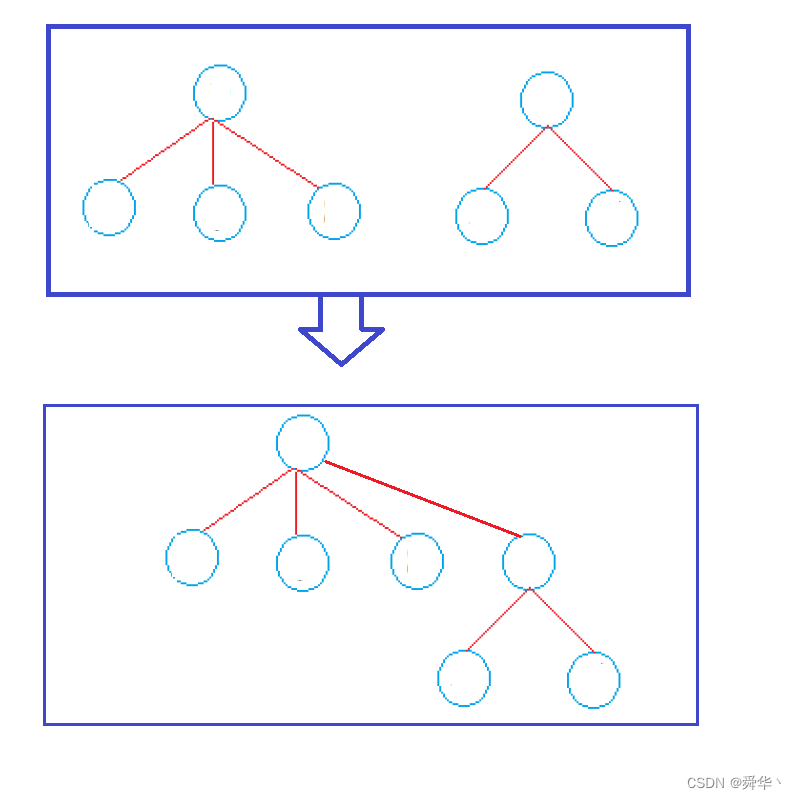
- 两个人产生关联,本质上是两个宿舍(集合)之间产生了关联,那两个宿舍如何进行关联起来呢?
- 下面我们以图的形式更为清晰的进行表述:
- 也就是说因为宿舍的成员是以宿舍长联系起来的,那宿舍与宿舍之间,产生关联(合并),就宿舍长之间认识一下,两个集合就间接的关联起来了。
- 下图是具体的存储方式:
2.基本实现
根据上面的描述,我们可以作出大致总结:
- 数组进行存储表示树形结构。
- 数组的下标对应着具体的信息(人名,编号等)。
- 我们可以通过一个元素的下标的值不断往上查找,直到找到找到小于0的,即为根节点所在的位置。
- 数组中负数的个数代表着集合的个数。
- 判断两个元素是否在同一个集合,只需找到根的下标判断是否相等即可。
- 将两个不同集合进行合并,其实就是找到根,然后进行更改一个根的指向与改变另一个根的元素个数即可。
由以上信息我们先可以搭建出实现并查集的大致框架:
2.1.基本框架
#include<iostream>
#include<vector>
#include<map>
using namespace std;
template<class T>
class UnionFindSet
{
public:UnionFindSet(const T* arr, size_t size);//构造函数int GetValueIndex(const T& val);//获取val所代表的下标。void GetRoot(const T& val);//获取根节点的下标void Union(const T& x1, const T& x2);//将两个元素的集合进行合并。bool IsSameSet(const T& x1, const T& x2);//判断两个元素是否在同一个集合中int GetSetSize(); //获取集合的元素
private:map<T, int> _indexHash;//map或者unordered_map都可以。用于快速将T转换为对应的下标。vector<T> _createIndex;//用此数组对T类型元素生成下标。vetor<int> _aggregate; //用于存放集合元素,即森林。
};
2.2.构造函数
UnionFindSet(const T* arr, size_t size){_aggreagte.resize(size, -1);//对存放集合的元素初始化,表示每个元素存放一个元素(负数表示)。_createIndex.resize(size);for (size_t i = 0; i < size; i++){_createIndex[i] = arr[i];_indexHash[arr[i]] = i;//生成下标。}}
2.3.转换元素为下标
int GetValueIndex(const T& val){auto it = _indexHash.find(val);//最好判断一下val是否存在对应的下标。if (it == _indexHash.end()){throw invalid_argument("不存在所对应的下标");return -1;}return it->second;}
2.4.获取元素根节点下标
int GetRoot(const T& val){int index = GetValueIndex(val);//找不到小于0的下标指向的位置就一直向上进行找。while (_aggregate[index] >= 0){index = _aggregate[index];}return index;}
2.5.判断元素集合是否相同
bool IsSameSet(const T& x1, const T& x2)/{int index1 = GetRoot(x1);int index2 = GetRoot(x2);return index1 == index2;}
2.6.合并元素集合
void Union(const T& x1, const T& x2)//将两个元素的集合进行合并。{if (!IsSameSet(x1, x2)){//不在同一个集合再进行合并。int index1 = GetRoot(x1);int index2 = GetRoot(x2);//进行一步优化,即元素少的合并到元素多的集合当中//此处我们假设index1为元素多的集合,index2为元素少的集合。if (abs(index1) < abs(index2)){swap(index1, index2);}//即将index2(少)合并到index1(多)上//将index2的元素加到index2上_aggregate[index1] += _aggregate[index2];//将index2的父路径指向index1_aggregate[index2] = index1;}}
2.7.获取集合个数
int GetSetSize()//获取并查集的集合个数{int sum = 0;for (auto e : _aggregate){//计算小于0的元素个数即可。if (e < 0){sum++;}}return sum;}
3.路径压缩
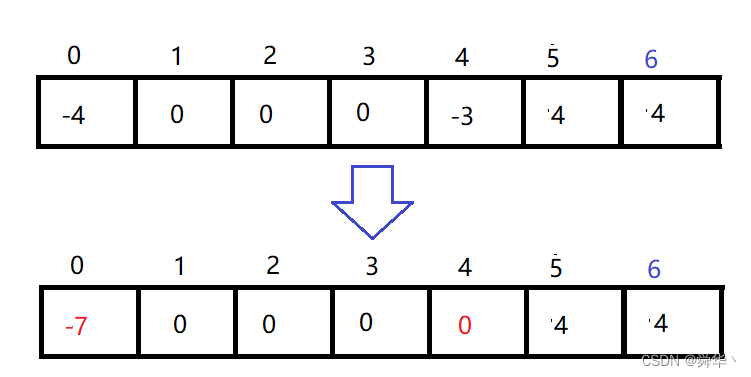
所谓路径压缩,其实解决存在这样的集合:
所引发的问题:如果数据足够的多,我们之前写的GetRoot函数的效率会急剧的降低,因此才需要路径压缩帮助我们进行优化。
实现方式也很简单:
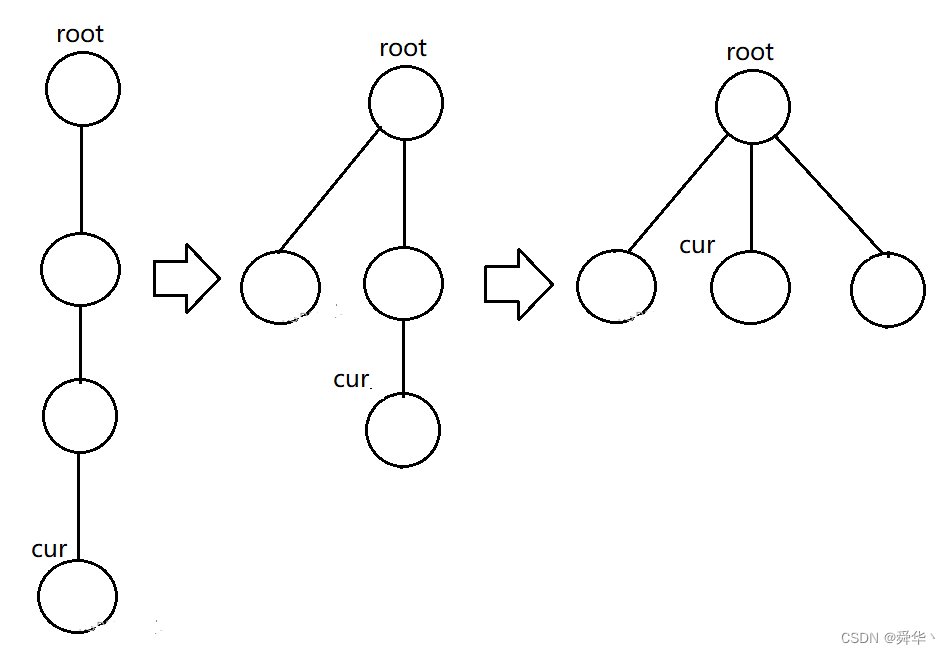
-
我们只需要找到根节点之后,再找一遍,此时将cur路径上的结点链接到root即可,这样方便了后续的查找。
-
优化之后的GetRoot
int GetRoot(const T& val)//获取根节点的下标{int index = GetValueIndex(val);int root = index;//找不到小于0的下标指向的位置就一直向上进行找。while (_aggregate[root] >= 0){root = _aggregate[root];}//路径压缩进行优化。while (index != root){//先保存之前父路径的下标int parent = _aggregate[index];//再将当前结点的父路径改为root_aggregate[index] = root;//继续往上迭代index = parent;}return root;}
4.源码与测试
- UnionFindSet.hpp
#include<iostream>
#include<vector>
#include<map>
using namespace std;
template<class T>
class UnionFindSet
{
public:UnionFindSet(const T* arr, size_t size){_aggregate.resize(size, -1);//对存放集合的元素初始化,表示每个元素存放一个元素(负数表示)。_createIndex.resize(size);for (size_t i = 0; i < size; i++){_createIndex[i] = arr[i];_indexHash[arr[i]] = i;//生成下标。}}int GetValueIndex(const T& val)//获取val所代表的下标。{auto it = _indexHash.find(val);if (it == _indexHash.end()){throw invalid_argument("不存在所对应的下标");return -1;}return it->second;}int GetRoot(const T& val)//获取根节点的下标{int index = GetValueIndex(val);int root = index;//找不到小于0的下标指向的位置就一直向上进行找。while (_aggregate[root] >= 0){root = _aggregate[root];}//路径压缩进行优化。while (index != root){//先保存之前父路径的下标int parent = _aggregate[index];//再将当前结点的父路径改为root_aggregate[index] = root;//继续往上迭代index = parent;}return root;}void Union(const T& x1, const T& x2)//将两个元素的集合进行合并。{if (!IsSameSet(x1, x2)){//不在同一个集合再进行合并。int index1 = GetRoot(x1);int index2 = GetRoot(x2);//进行一步优化,即元素少的合并到元素多的集合当中//此处我们假设index1为元素多的集合,index2为元素少的集合。if (abs(index1) < abs(index2)){swap(index1, index2);}//即将index2(少)合并到index1(多)上//将index2的元素加到index2上_aggregate[index1] += _aggregate[index2];//将index2的父路径指向index1_aggregate[index2] = index1;}}//判断两个元素是否在同一个集合中bool IsSameSet(const T& x1, const T& x2){int index1 = GetRoot(x1);int index2 = GetRoot(x2);return index1 == index2;}int GetSetSize()//获取并查集的集合个数{int sum = 0;for (auto e : _aggregate){if (e < 0){sum++;}}return sum;}
private:map<T, int> _indexHash;//map或者unordered_map都可以,用于快速将T转换为对应的下标。vector<T> _createIndex;//用此数组对T类型元素生成下标。vector<int> _aggregate; //用于存放集合元素,即森林。
};
- Test.cpp
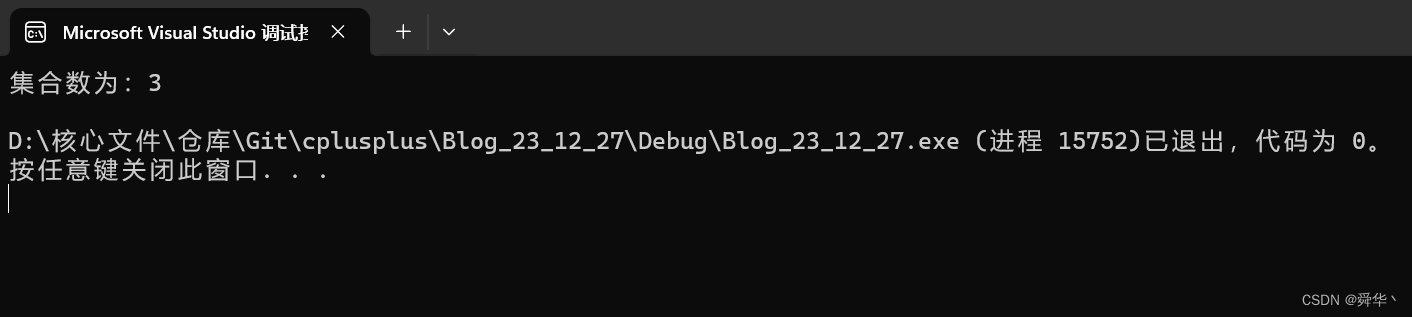
#include"UnionFindSet.hpp"
int main()
{string str[] = { "张三","李四","王五","赵六","周七" };UnionFindSet<string> ufs(str, sizeof(str) / sizeof(str[0]));ufs.Union("张三", "李四");ufs.Union("王五", "赵六");cout << "集合数为:" << ufs.GetSetSize() << endl;return 0;
}
运行结果:
并查集习题:
- 省份数量
- .等式方程的可满足性
- 补充一下:
- 直接用下标进行抽象,是最常用的,因此这里的生成下标的vector与快速索引的map可以省去,形成一个简化版的并查集,更方便我们使用。
- 这里我们将并查集与图论放在一起,是因为
并查集可以帮助起到判环的作用,因此我们这里放到一块进行讲解。
二、图论
1.基本概念
- 图的概念有点凌乱,博主以思维导图的形式呈现出:

2.存储结构
- 图有两个基本元素:
- 顶点, 我们可以将具体的顶点抽象成下标,从而用下标进行表示。
- 边,两个顶点即可确定一条边,因此我们可以用二维矩阵的方式进行表示;每个顶点都有与其相连的边,因此,我们可以单独每个顶点所连接的边抽象成桶的形式(类似于哈希桶)进行表示。
- 因此我们通常有邻接矩阵和邻接表的形式进行存储。
2.1邻接矩阵
- 实现代码:
/*V(vertex) 表示实际存储边的类型,W(weight)表示边的权重,W_MAX 表示权重的不可能取值。Direction false表示是无向的,true表示是有向的。*/template<class V, class W, W W_MAX = INT_MAX, bool Direction = false>class Graph{public:/*构造函数,传入的参数为V类型的指针指向的是V类型数组,以及数组的元素个数。*/Graph(const V* a, size_t n)//有多少个顶点{//初始化边,以及生成边的下标_vertexs.resize(n);for (size_t i = 0; i < n; i++){_vertexs[i] = a[i];_indexMap[a[i]] = i;}//将矩阵进行初始化_matrices.resize(n);for (size_t i = 0; i < n; i++){//没有权值,我们初始化为W_MAX,表示最开始顶点之间不互相连通。_matrices[i].resize(n, W_MAX);}}//将实际的顶点转换为对应的下标int GetVertexIndex(const V& v){auto it = _indexMap.find(v);if (it == _indexMap.end()){//找不到throw invalid_argument("顶点不存在");//抛出异常return -1;}return it->second;}//添加边void AddEdge(const V& src, const V& dst, const W& w){int srci = GetVertexIndex(src);int dsti = GetVertexIndex(dst);_AddEdge(srci, dsti, w);}//这里我们写一个子函数,方便内部接口进行使用。void _AddEdge(int srci, int dsti, const W& w){_matrices[srci][dsti] = w;if (Direction == false){//说明是无向图_matrices[dsti][srci] = w;}}//为了方便进行测试,这里博主将打印函数给出。void Print(){for (size_t i = 0; i < _vertexs.size(); i++){printf("[%d]->", i);cout << _vertexs[i] << endl;//下标对应的边}cout << " ";for (size_t i = 0; i < _matrices.size(); i++)printf("%-4d", i);cout << endl;for (size_t i = 0; i < _matrices.size(); i++){printf("%-4d",i);for (size_t j = 0; j < _matrices[i].size(); j++){if (_matrices[i][j] != W_MAX)printf("%-4d", _matrices[i][j]);elseprintf("%-4c", '*');}cout << endl;}cout << endl;}vector<V> _vertexs;//顶点map<V, int> _indexMap;//顶点所对应的下标vector<vector<W>> _matrices; //矩阵的英文};
- 说明:
- 如果边带有权值,并且两个节点之间是连通的,边的关系就用权值代替。
- 如果两个顶点不通,则使用无穷大代替,即W_MAX。
- 测试用例:
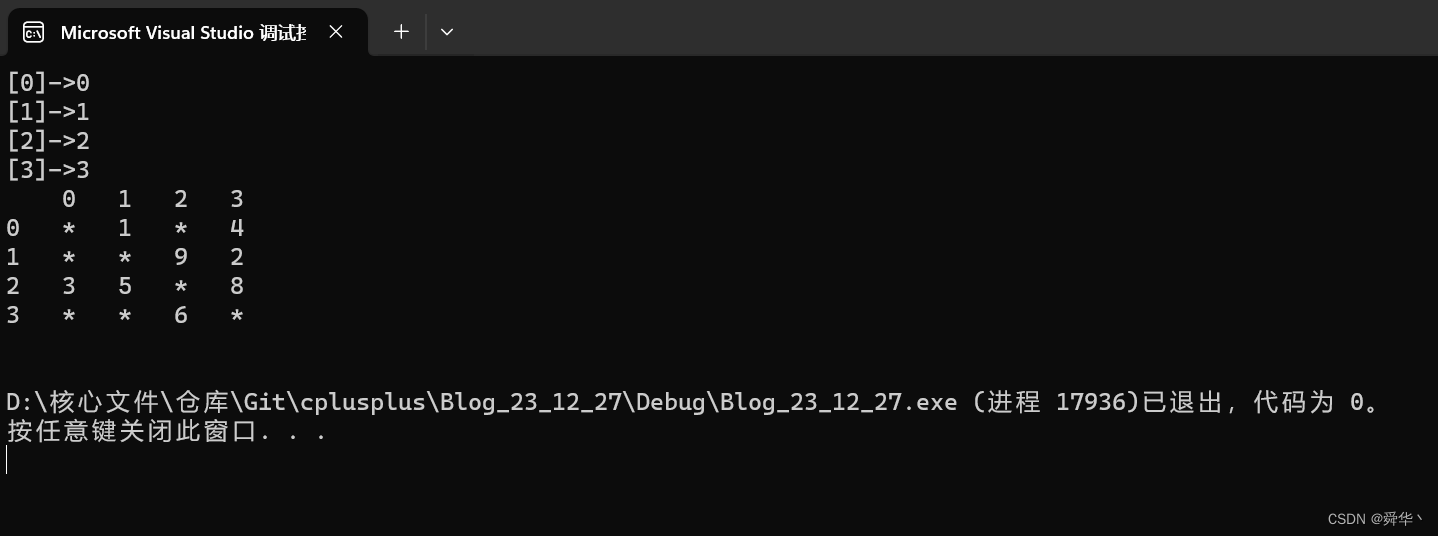
void TestGraph()
{Graph<char, int, INT_MAX, true> g("0123", 4);g.AddEdge('0', '1', 1);g.AddEdge('0', '3', 4);g.AddEdge('1', '3', 2);g.AddEdge('1', '2', 9);g.AddEdge('2', '3', 8);g.AddEdge('2', '1', 5);g.AddEdge('2', '0', 3);g.AddEdge('3', '2', 6);g.Print();
}
int main()
{TestGraph();return 0;
}
运行结果:
2.2邻接表
- 实现代码:
namespace link
{/*因为要存顶点与边的关系,因此我们需要一个结构体来保存对应的相连的顶点与边的权值。*/template<class V,class W>struct Edge{V _dst;//目标顶点W _w;//权值Edge<V, W>* _next;//构造函数Edge(const V& dst, const W w):_dst(dst),_w(w),_next(nullptr){}};template<class V, class W, bool Direction = false>class Graph{public:typedef Edge<V, W> Edge;Graph(const V* a, size_t n)//有多少个顶点{//初始化边,以及生成对应的下标_vertexs.resize(n);for (size_t i = 0; i < n; i++){_vertexs[i] = a[i];_indexMap[a[i]] = i;}//将矩阵进行初始化,为空表示最开始顶点没有边与之相连。_link.resize(n,nullptr);}//添加边void AddEdge(const V& src, const V& dst, const W& w){int srci = GetVertexIndex(src);int dsti = GetVertexIndex(dst);Edge* node = new Edge(dst, w);node->_next = _link[srci];_link[srci] = node;if (Direction == false){//说明是无向图Edge* node = new Edge(src, w);node->_next = _link[dsti];_link[dsti] = node;}}//获取顶点的下标。int GetVertexIndex(const V& v){auto it = _indexMap.find(v);if (it == _indexMap.end()){//找不到throw invalid_argument("顶点不存在");//抛出异常return -1;}return it->second;}//打印的时候我们按照链表的形式打印即可。void Print(){for (size_t i = 0; i < _link.size(); i++){cout << "[" << i << ":" << _vertexs[i] << "]->";Edge* cur = _link[i];while (cur){cout << "[" << cur->_dst << ":" << _indexMap[cur->_dst] << ":" << cur->_w << "]->";cur = cur->_next;}cout << "nullptr" << endl;}cout << endl;}private:vector<V> _vertexs;//顶点map<V, int> _indexMap;//顶点所对应的下标vector<Edge*> _link; //邻接表};
}
- 测试用例:
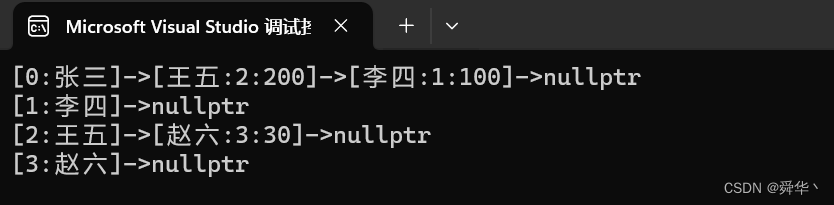
void TestGraph()
{string a[] = { "张三", "李四", "王五", "赵六" };Graph<string, int,true> g1(a, 4);g1.AddEdge("张三", "李四", 100);g1.AddEdge("张三", "王五", 200);g1.AddEdge("王五", "赵六", 30);g1.Print();
}
运行结果:
- 总结:
- 邻接矩阵适合快速查看两个顶点的关系与路径权值。而对于顶点连接的边有多少,是什么,则需要遍历矩阵所在行进行确认。
- 邻接表适合直接取所有与点相连的边,而不适合快速查看两个顶点的关系。
- 因此邻接矩阵和邻接表是相辅相成的,而综合来看的话,对于较为稀疏的图,即顶点相连的边较少,平分秋色,各有千秋,而对于稠密的完全图来说,邻接矩阵更为合适。因此我们下面统一采用临界矩阵的方式进行实现。
3.遍历方式
3.1广度优先遍历
- 图解:
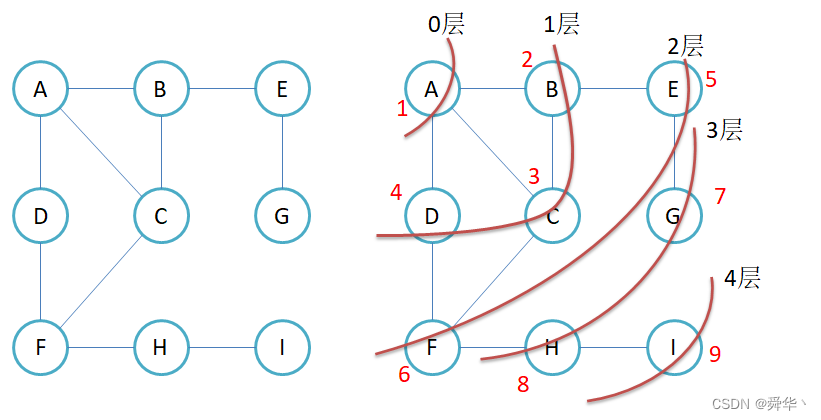
我们再来分析一下流程,这里是以A为起点,进行广度遍历。
- 先遍历A,。
- 然后遍历与A相连的BCD。
- 其次在遍历与BCD相连的EF,此时就需要注意之前访问过的结点不能在接着继续访问了。
- 接着遍历与EF相连的HG,此时也需注意同样的问题。
- 最后遍历与H相连的I,此时同理。
- 因此广度优先遍历,需注意访问的时候不能再访问已经访问过的结点,其次访问时越访问越深的。
实现方式:
- 采用队列的结构,不断入与队列元素相连的未访问的结点。
- 使用一个vector 记录结点是否已经被访问过了,当入队列时,即将对应的结点的下标标记为true。
void BFS(const V& src)
{int srci = GetVertexIndex(src);int n = _vertexs.size();vector<int> is_visited(n, false);//防止重复结点入队列,以免形成回路。queue<int> que;que.push(srci);is_visited[srci] = true;int levelsize = 1;//第一层就srci.while (!que.empty()){for (int i = 0; i < levelsize; i++){int front = que.front();que.pop();cout << front << ":" << _vertexs[front] << " ";//将与front相关的边进行入队列for (int i = 0; i < n; i++){if (_matrices[front][i] != W_MAX &&is_visited[i] == false){que.push(i);is_visited[i] = true;}}//这一层for循环式暴力遍历矩阵的所在行,确认是否有//没被访问的边。如果是邻接表就直接取较为方便,不过//稠密图倒是矩阵更优一点,能更好的确认两点的关系。 }cout << endl;//更新层结点的个数。levelsize = que.size();}
}
- 测试用例:
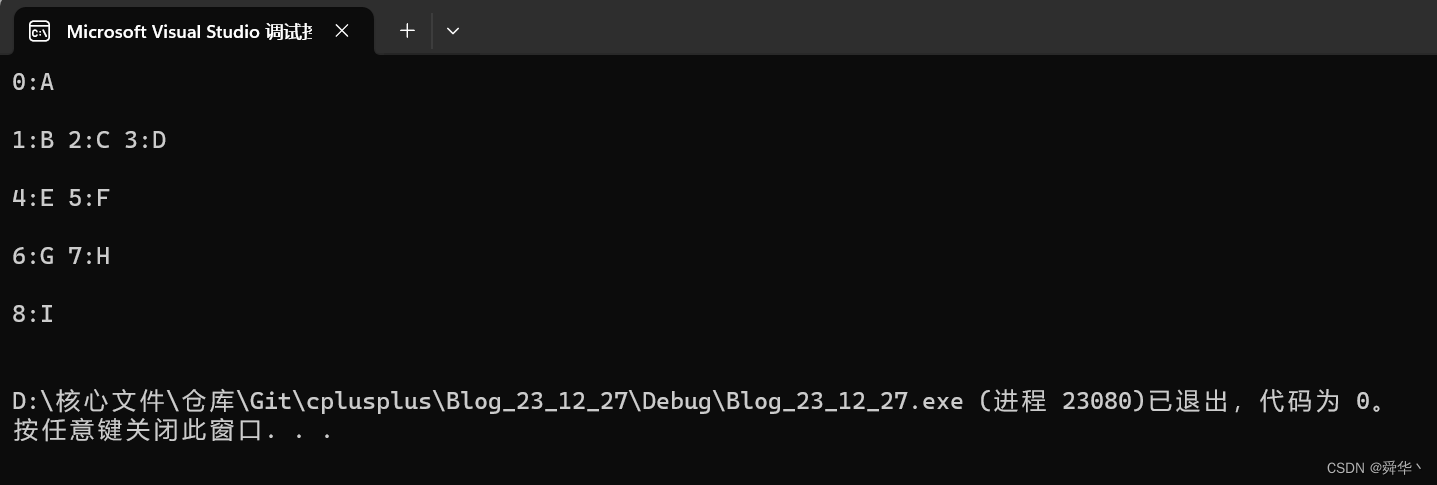
void TestBFS(){string a[] = { "A", "B", "C", "D", "E","F","G","H","I" };Graph<string, int> g1(a, sizeof(a) / sizeof(string));g1.AddEdge("A", "B", 1);g1.AddEdge("A", "C", 1);g1.AddEdge("A", "D", 1);g1.AddEdge("B", "E", 1);g1.AddEdge("B", "C", 1);g1.AddEdge("C", "F", 1);g1.AddEdge("C", "B", 1);g1.AddEdge("D", "F", 1);g1.AddEdge("E", "G", 1);g1.AddEdge("F", "H", 1);g1.AddEdge("H", "I", 1);g1.BFS("A");}
- 运行结果:
3.2深度优先遍历
- 图解:
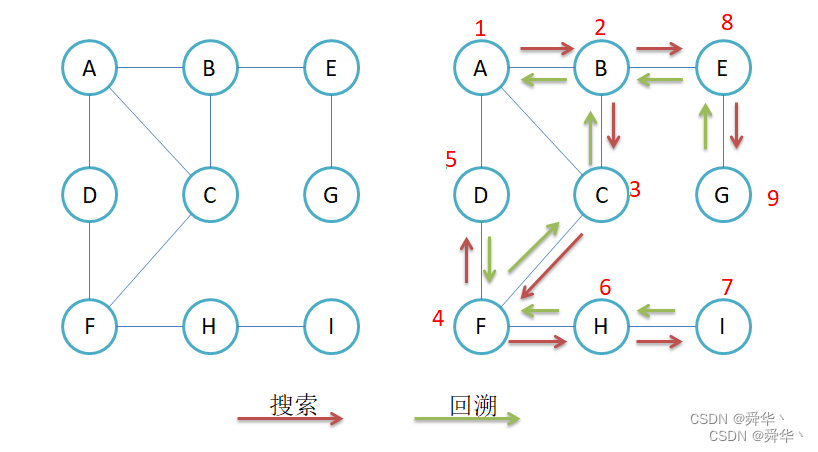
我们再来分析一下流程,这里是以A为起点,进行深度遍历。
说明:已经访问过的结点我们是不再进行访问的。
- 先访问A相邻的B, 再访问与B相连的C, 再访问与C相连的F, 再访问与F相连的D。
- D相邻的A我们是不再进行访问的,因此又回到F, 接着访问H,紧接着访问与H相连的I,I没有访问过的结点,回退到H, H也没有访问过的结点回退到 F。
- F也没有与未访问的结点,回退到C,C也没有未访问的结点,于是回退到B。
- 接着访问与B相连的E, 更深一步访问与E相连的G,G没有未访问过的结点,回退到E, E此时也没有未访问过的结点回退到B, B此时也没有未访问过的结点,回退到A.
- 访问结束。
- 实现代码:
void _DFS(int srci,vector<bool>& is_visted){for (size_t i = 0; i < is_visted.size(); i++){if (_matrices[srci][i] != W_MAX && is_visted[i] == false){//此处打印的目的是便于测试。cout << "[" << _vertexs[srci] << "->" << _vertexs[i] << "]" << endl;is_visted[i] = true;_DFS(i, is_visted);}}}void DFS(const V& src){int srci = GetVertexIndex(src);vector<bool> is_visted(_vertexs.size(), false);is_visted[srci] = true;_DFS(srci,is_visted);}
- 测试用例:
void TestDFS()
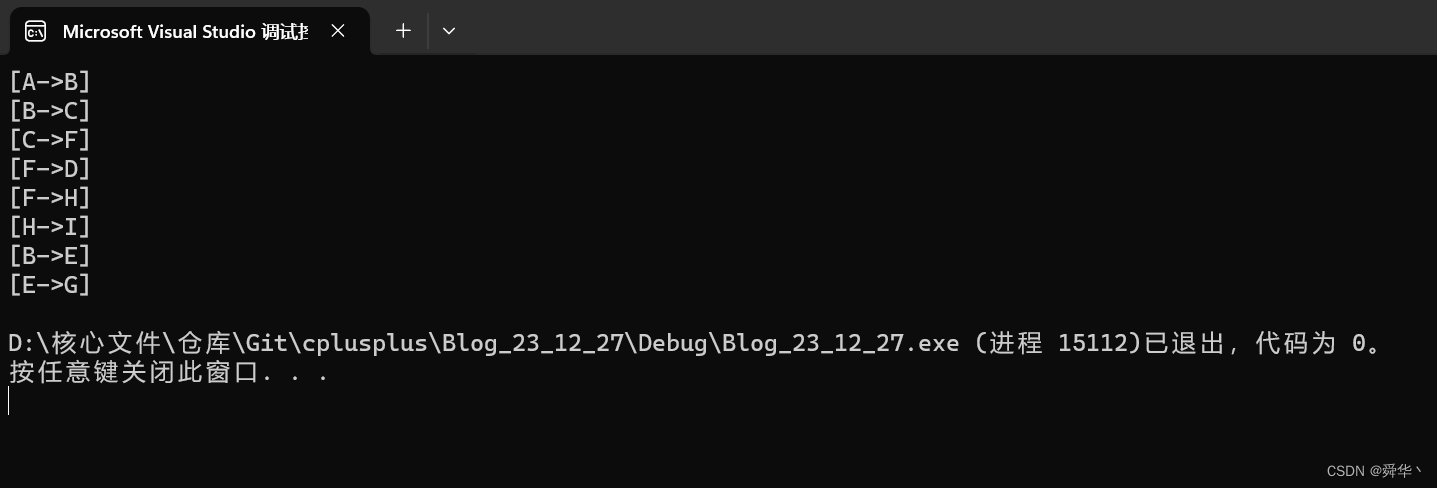
{string a[] = { "A", "B", "C", "D", "E","F","G","H","I" };Graph<string, int> g1(a, sizeof(a) / sizeof(string));g1.AddEdge("A", "B", 1);g1.AddEdge("A", "C", 1);g1.AddEdge("A", "D", 1);g1.AddEdge("B", "E", 1);g1.AddEdge("B", "C", 1);g1.AddEdge("C", "F", 1);g1.AddEdge("C", "B", 1);g1.AddEdge("D", "F", 1);g1.AddEdge("E", "G", 1);g1.AddEdge("F", "H", 1);g1.AddEdge("H", "I", 1);g1.DFS("A");
}/*主函数就自由发挥吧。*/
- 运行结果:
4.最小生成树
先来熟悉一下概念:
- 最小生成树:图的生成树的路径最小。
- 生成树:一个连通图的最小连通子图称作该图的生成树。有n个顶点的连通图的最小连通子图有n个顶点和n-1条边。
- 连通图:若从顶点v1到顶点v2有路径,则称顶点v1与顶点v2是连通的。如果图中任意一对顶点都是连通的,则称此图为连通图。
- 注意:连通图是无向图的概念,也就是说最小生成树的图必须是无向的。强连通图才是有向图的定义。
简单的说就是从由n个顶点组成的连通图中选择n-1条边,子图连通且所边的权值相加最小。
实现方法下面介绍克鲁斯卡尔和普里姆两种算法。
4.1Kruskal算法
- 原理
- 首先将所有的边管理起来,每次取出最小的边。
- 判断已经选出的边是否构环,如果构成就弃置再从中选最小的边。
- (n个顶点构成的图)选择n-1条边即可。
- 实现关键
- 用优先级队列对边进行管理。
- 用并查集进行判环。
- 实现代码:
/*
为方便读者进行阅读,此处博主贴了一份并查集的简略代码。
*/template<class T>class UnionFindSet{public://初始化大小,以及赋初值UnionFindSet(size_t size):_pPath(size, -1){}//将两个数进行合并void Union(int x1, int x2){//找两个数的父结点int index1 = find(x1);int index2 = find(x2);//如果相同则说明已经在同一个集合下,无需进行合并if (index1 == index2) return;//将小的和在大的身上(优化防止路径过长)if (_pPath[index1] < _pPath[index2]){swap(index1, index2);swap(x1, x2);}//此处保证index1的父节点的数量多,index2的数量小_pPath[index1] += _pPath[index2];_pPath[index2] = index1;}//找根int GetValueIndex(int x){//第一步:转换为下标int index = x;//第二步:根据下标找父节点while (_pPath[index] >= 0){index = _pPath[index];}//找到父路径进行返回。//路径压缩while (x != index){int parent = _pPath[x];_pPath[x] = index;x = parent;}return index;}int setsize(){int n = 0;for (int e : _pPath)if (e < 0) n++;return n;}private:vector<int> _pPath;};/*此结构体用于存放边的信息,放入优先级队列中便于进行管理。*/template<class W>struct Edge{int _srci;int _dsti;W _w;Edge(const int srci, const int dsti, const W& w):_srci(srci), _dsti(dsti), _w(w){}bool operator >(const Edge e) const{return _w > e._w;}};W Kruskal(self& min){min._vertexs = _vertexs;//第一步,用优先级队列存放所有的边priority_queue<Edge, vector<Edge>, greater<Edge>> minque;size_t n = _vertexs.size();//无向图,只需存放一半的图的信息即可。for (size_t i = 0; i < n; i++){for (size_t j = 0; j < i; j++){if (_matrices[i][j] != W_MAX){minque.push(Edge(i, j, _matrices[i][j]));}}}//第二步,选边,最小生成树,选择的边为 n-1条边size_t size = 0;UnionFindSet<int> u(n);W total = W();while (!minque.empty() && size != n-1){Edge top = minque.top();minque.pop();if (u.find(top._dsti) != u.find(top._srci)){//说明不构成环,选择此边,并将其加入到并查集和表中//此处是为了方便测试。cout << _vertexs[top._dsti] << "->" << _vertexs[top._srci]<< ":" << top._w << endl;u.Union(top._dsti, top._srci);min._AddEdge(top._dsti, top._srci, top._w);size++;total += top._w;}}//队列为空跳出循环,因此需要判断一下看是否选出了n-1条边。if (size != n - 1){//表明不能选出来return W();}return total;}
- 测试用例:
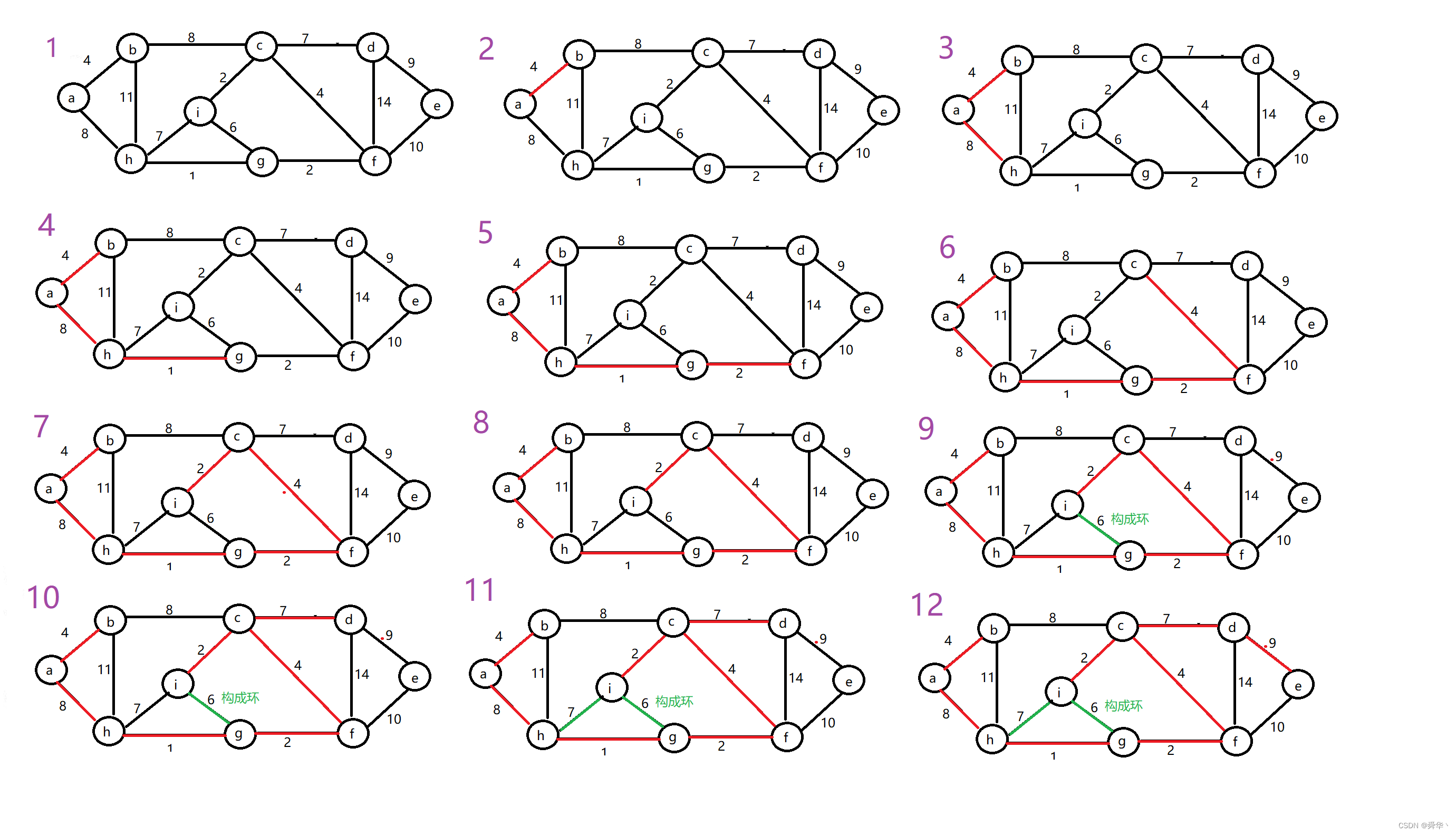
void TestGraphMinTree(){const char* str = "abcdefghi";Graph<char, int> g(str, strlen(str));g.AddEdge('a', 'b', 4);g.AddEdge('a', 'h', 8);//g.AddEdge('a', 'h', 9);g.AddEdge('b', 'c', 8);g.AddEdge('b', 'h', 11);g.AddEdge('c', 'i', 2);g.AddEdge('c', 'f', 4);g.AddEdge('c', 'd', 7);g.AddEdge('d', 'f', 14);g.AddEdge('d', 'e', 9);g.AddEdge('e', 'f', 10);g.AddEdge('f', 'g', 2);g.AddEdge('g', 'h', 1);g.AddEdge('g', 'i', 6);g.AddEdge('h', 'i', 7);Graph<char, int> kminTree(strlen(str));cout << "Kruskal:" << g.Kruskal(kminTree) << endl;}
/*main函数自由发挥吧*/
-
运行结果:
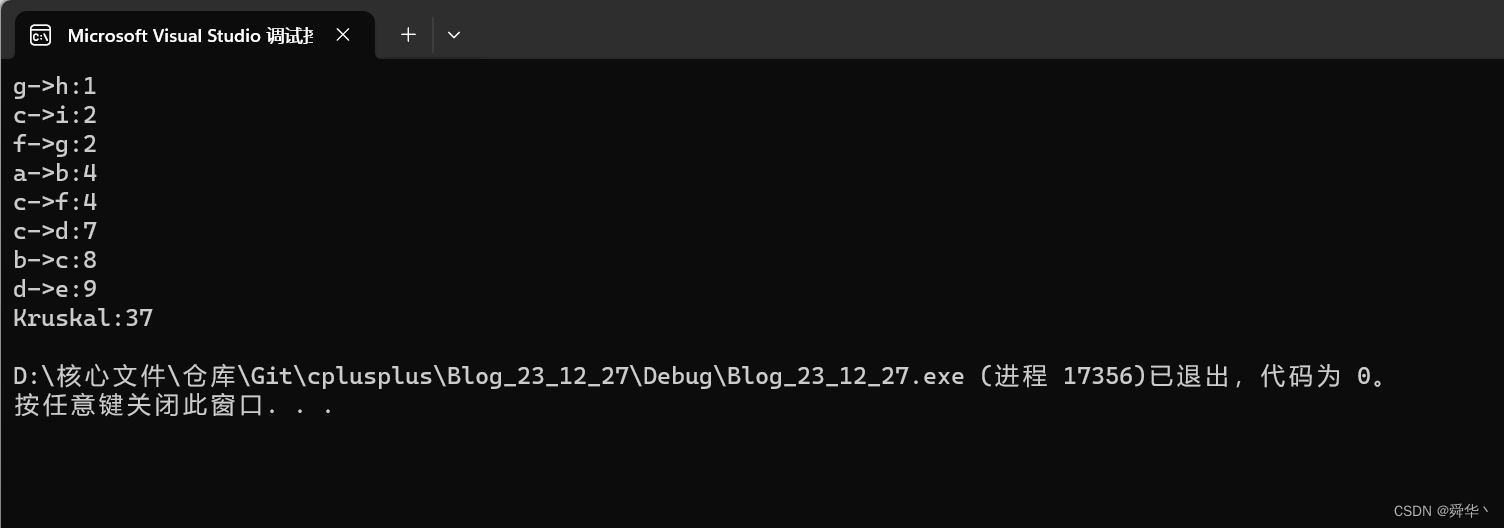
-
图解:
说明:
- 程序走出的过程可能不一样,比如相同的边谁先选可能由优先级的实现原理决定,但大概率结果是一样的。
- 我们走出的只是局部的最优解,全局的最优解,可能还与相同的边的选择顺序有关,相同的边的如果互相影响,则可能会影响后面更大的边的选择。
- 因此如果所有的边互不相同那我们可以断定,此算法走出的最小生成树是确定的,即为全局的最小生成树。
4.2Prim算法
- 原理
- 将顶点分为两个集合,设一个集合为X, 一个集合为Y。
- 选择一个起始点,放入X集合,剩余的顶点放入Y集合。
- 每次选择从Y中选择与X相连的最小的边,并将其相连的顶点放入X集合,从Y中丢弃此顶点。
- 直到选择 n - 1条边为止。
- 实现关键:
- 将顶点分为两个集合X, Y,其实就避开了环的问题,产生环的原因本质就是一个集合内的两个顶点连到一块了。
- 我们选的是与集合X相连的最小的边,因此还要把X相连的边,放入优先级队列,往后循环可能会有一个集合内的边,我们只需判断边所连的目标顶点不在集合X即可,对于在集合X的我们不选即可。
- 除此之外,我们还需要确立一个起始点,用来初始化集合X和集合Y。
- 实现代码:
W Prim(self& min,const V& src){size_t n = _vertexs.size();min._vertexs = _vertexs;/*第一步:选择顶点,作为起始顶点。分为两个数组,一个为起始数组,一个为选边数组*/int srci = GetVertexIndex(src);vector<bool> X(n,false);vector<bool> Y(n,true);X[srci] = true;Y[srci] = false;//第二步:将与srci相关的边入队列中。priority_queue<Edge, vector<Edge>, greater<Edge>> minque;for (size_t i = 0; i < n; i++){//将边进行入队列if (_matrices[srci][i] != W_MAX){minque.push(Edge(srci, i, _matrices[srci][i]));}}//第三步进行选边W total = W();size_t size = 0;while (!minque.empty()){Edge front = minque.top();minque.pop();//判断边的终点是否在X中if (X[front._dsti]){//说明构成环。cout << "构成环:";cout << _vertexs[front._srci] << "->" << _vertexs[front._dsti] << endl;}else{cout << _vertexs[front._srci] << "->" << _vertexs[front._dsti] << endl;++size;total += front._w;//将边添加到最小生成树里面,并将与dsti相连的边入队列min._AddEdge(front._srci, front._dsti, front._w);//将desi所在的集合进行删除与添加Y[front._dsti] = false;X[front._dsti] = true;//将dsti所连的边进行入队列for (size_t i = 0; i < n; i++){//避免将已经入过的边再进行入队列if (_matrices[front._dsti][i] != W_MAX && Y[i]){//不在X[i] 即将在Y[i]进行入队列。minque.push(Edge(front._dsti, i,_matrices[front._dsti][i]));}}}}//如果不能生成最小生成树。if (size != n - 1){return W();}return total;}
- 测试代码:
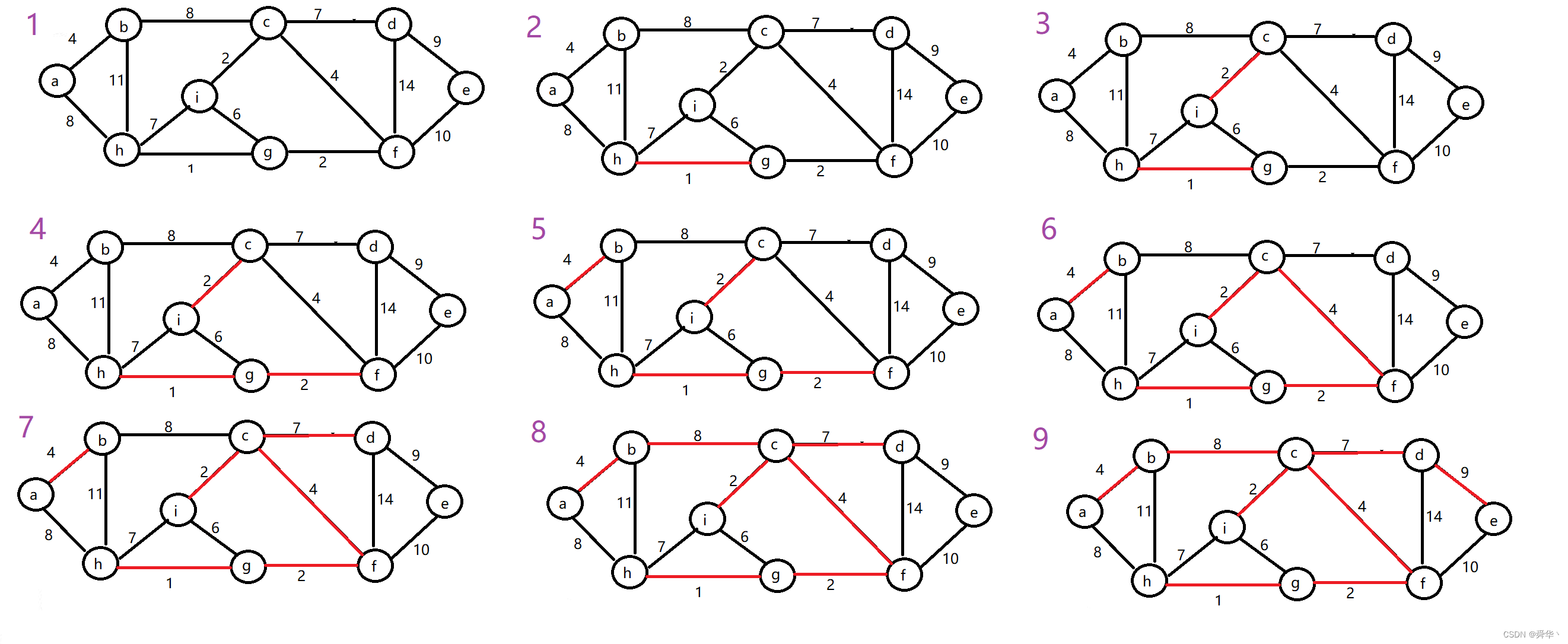
void TestGraphMinTree(){const char* str = "abcdefghi";Graph<char, int> g(str, strlen(str));g.AddEdge('a', 'b', 4);g.AddEdge('a', 'h', 8);//g.AddEdge('a', 'h', 9);g.AddEdge('b', 'c', 8);g.AddEdge('b', 'h', 11);g.AddEdge('c', 'i', 2);g.AddEdge('c', 'f', 4);g.AddEdge('c', 'd', 7);g.AddEdge('d', 'f', 14);g.AddEdge('d', 'e', 9);g.AddEdge('e', 'f', 10);g.AddEdge('f', 'g', 2);g.AddEdge('g', 'h', 1);g.AddEdge('g', 'i', 6);g.AddEdge('h', 'i', 7);Graph<char, int> pminTree(strlen(str));cout << "Prim:" << g.Prim(pminTree, 'a') << endl;pminTree.Print();}
/*main 函数只需调用此函数即可*/
运行结果:
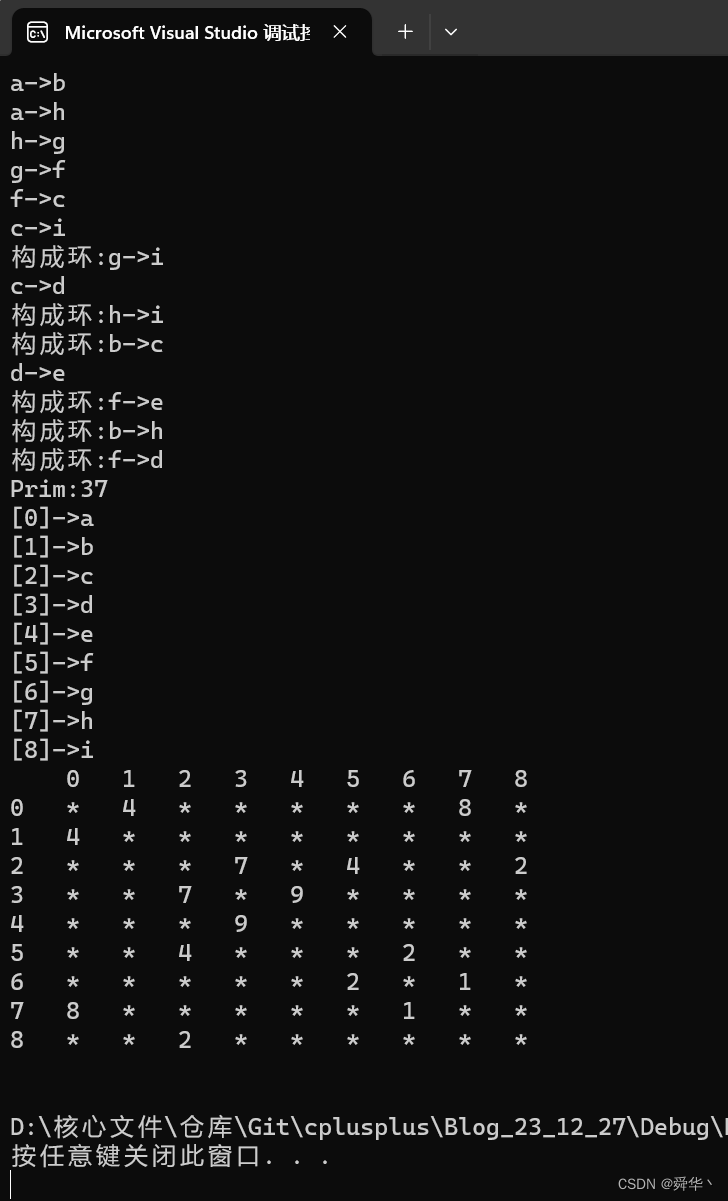
- 图解:
5.最短路径
- 最短路径是描述两个顶点能连通的情况下,考虑两个顶点之间所经过路径的权值之和的最小值。
- 举个例子,在现实世界中我们已经不关心两个地方能不能到的问题了,我们主要关系的是两个地方如何规划路程最短或者花费最低,诸如此类的问题,抽象到计算机即转换为了两个顶点所经过的路径的权值之和如何才能最短。
由此,我们引出迪杰斯特拉(Dijkstra), 贝尔曼福特(Bellman-Ford), 弗洛伊德(floyd warshall) 三种算法。
5.1Dijkstra算法
- 基本认识
此算法主要求的是不带负权值最小路径。
算法思想主要在单源最短路径中进行体现。
- 算法原理(贪心)
- 确定一个起始点,更新与其
直接相连的顶点的路径。- 选择路径和最短的那一个,此处
确定了第一条路径最短的边。
- 确定两字我们此处再稍作解释,由于已经选择了起始点直接到路径最短的顶点。因此不可能再出现,从起始点到另一个顶点再经过其它顶点到此点的路径和更短,更简单的表述是两点直接连着已经最短的了,再通过其它点绕远路只会更长,不会更短。
- 此处用数学的语言进行描述或许更加直观。
- 再由最短的那个顶点,再更新(如果更小再进行更新)与其直接相连的边,再确定一条路径最短的边的顶点。由此顶点再进行更新。
- 如此往复,直到没有顶点可以更新,就结束。
- 实现代码:
void Dijkstra(const V& src, vector<W>& dst, vector<int>& pPath){//将边与路径进行初始化size_t n = _vertexs.size();int srci = GetVertexIndex(src);//值初始化为W_MAXdst.resize(n, W_MAX);//路径初始化为-1pPath.resize(n, -1);//src->src路径值初始化为W(),路径初始化为srcidst[srci] = W();pPath[srci] = srci;//创建一个bool的vector使得每个结点只访问一次vector<bool> is_visted(n, false);for (size_t i = 0; i < n; i++){W min = W_MAX;int vertexi = 0;//先选出没被访问过的最小的边for (size_t j = 0; j < n; j++){if (!is_visted[j] && dst[j] < min){min = dst[j];vertexi = j;}}//选出之后标记为选过的边is_visted[vertexi] = true;//再进行松弛更新与其相连的边for (size_t j = 0; j < n; j++){/*首先得有边,且是顶点没有访问的点,并且 srci->vertex + vertex->j < srci->j,再进行更新*/ if (_matrices[vertexi][j] != W_MAX && !is_visted[j]&& dst[vertexi] + _matrices[vertexi][j] < dst[j]){//更新j的父路径和srci->j的距离pPath[j] = vertexi;dst[j] = dst[vertexi] + _matrices[vertexi][j];}}}}
- 此处对这里的pPath进行说明一下,是将路径进行压缩从二维降到了一维,但其实也很简单,本质与并查集的路径表示大致一样,下标存的是父节点的下标。
- 另外,这里打印时因为每个结点表示的是父结点的下标,因此我们还需将路径倒着找到之后,再翻转成正向的,再进行打印。
- 打印最短路径函数:
void PrinrtShotPath(const V& src, vector<W>& dst, vector<int>& pPath)
{int srci = GetVertexIndex(src);size_t n = _vertexs.size();//先找到路径再进行逆置for (size_t i = 0; i < n; i++){//不能是srci,要不然就陷入环了。if (i != srci){vector<int> path;int parent = i;while (parent != srci){path.push_back(parent);parent = pPath[parent];}//最后将srci根结点入进去path.push_back(srci);//逆转path得到路径reverse(path.begin(), path.end());for (auto index : path){cout << _vertexs[index] << "->";}//最后打印出路径值cout << "最短路径值为:" << dst[i] << endl;}}
}
- 测试用例:
void TestGraphDijkstra(){const char* str = "syztx";Graph<char, int, INT_MAX, true> g(str, strlen(str));g.AddEdge('s', 't', 10);g.AddEdge('s', 'y', 5);g.AddEdge('y', 't', 3);g.AddEdge('y', 'x', 9);g.AddEdge('y', 'z', 2);g.AddEdge('z', 's', 7);g.AddEdge('z', 'x', 6);g.AddEdge('t', 'y', 2);g.AddEdge('t', 'x', 1);g.AddEdge('x', 'z', 4);vector<int> dist;vector<int> parentPath;g.Dijkstra('s', dist, parentPath);g.PrinrtShotPath('s', dist, parentPath);}
-
运行结果:
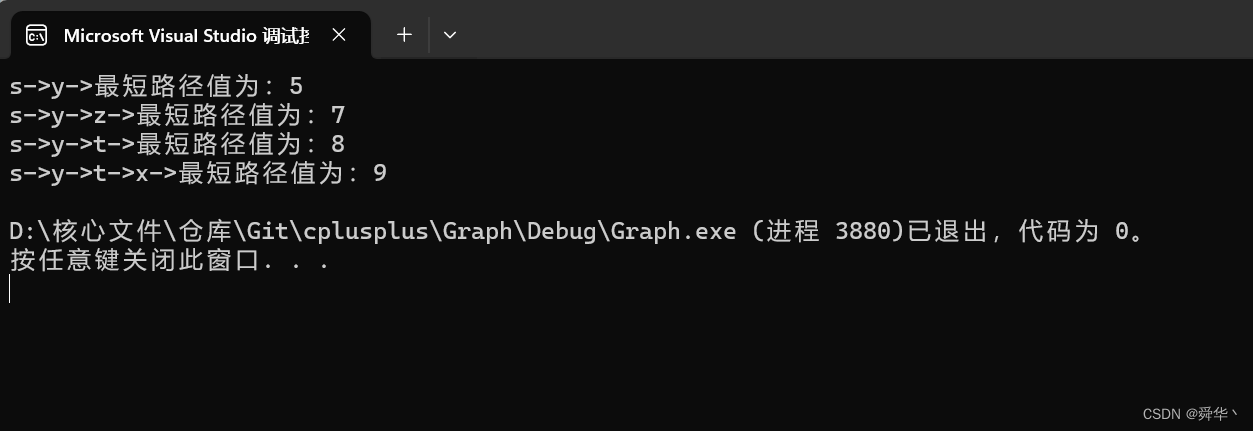
-
图解:
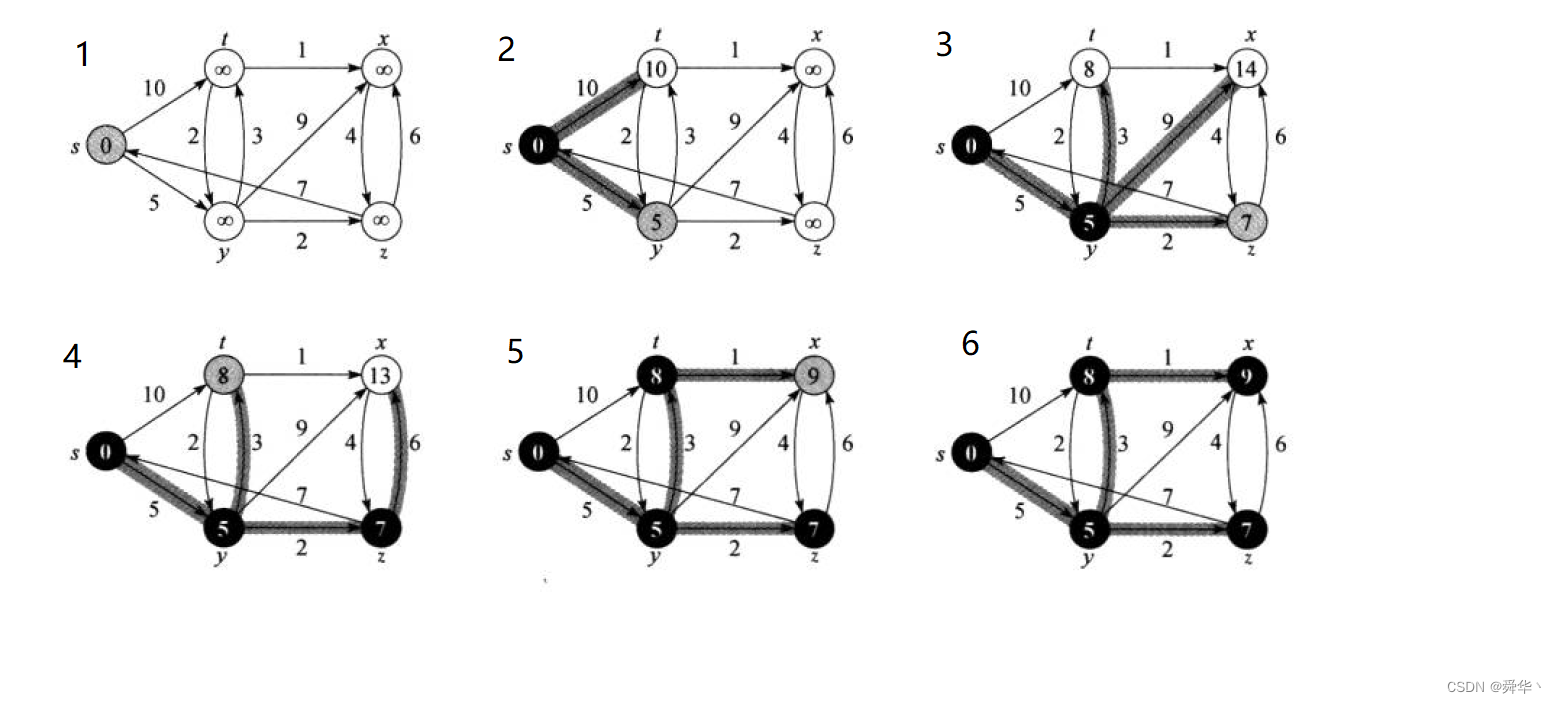
5.2Bellman-Ford算法
-
用处:单源最短路径的负权值(不带负权回路)的图
-
思想:暴力枚举遍历
- 由于只会更新出更短的路径,我们可以采取暴力枚举的方法。
- 将所有的边进行遍历,之后再遍历 n - 1 次进行修正。
- 重点就在于: 为什么
再遍历n - 1次?我们先来讨论一下,假设你再某次更新s->x->t->z 之后,s->x->t 出现了更短的路径(存在负权值,就有可能),更新成了s->y->t,但是原来已经更新的s->x->t->z虽然路径随着s->y->t更新,但是其s->t的权值并没有进行更新,这就导致了数据对不上的问题,因此我们需要再进行更新一轮,使之数据一致。而再次更新,有可能会导致其它最短路径的权值对不上,因此还要再进行更新,直到所有的最短路径都对上为止,因此最多要n-1次,带上最开始的那一次,总共n次。
- 实现代码:
bool BellmanFord(const V& src, vector<W>& dst, vector<int>& pPath)
{//将边与路径进行初始化size_t n = _vertexs.size();int srci = GetVertexIndex(src);//值初始化为W_MAXdst.resize(n, W_MAX);//路径初始化为-1pPath.resize(n, -1);//src->src路径值初始化为W(),路径初始化为srcidst[srci] = W();pPath[srci] = srci;for (size_t k = 0; k < n; k++){//更新n轮,因为一个路径更新出更短的路径,会影响其它路径的权值,//因此需要再次更新。//一轮之后,更新出最短路径,则其它路径的权值需要暴力更新一遍。//不带第一轮,最多更新n-1轮->其中每一轮都更新出了最短路径。bool update = false;for (size_t i = 0; i < n; i++){for (size_t j = 0; j < n; j++){//边存在,并且 s->i + i->j < s->j if (_matrices[i][j] != W_MAX && dst[i] + _matrices[i][j] < dst[j]){update = true;//更新父路径和权值pPath[j] = i;dst[j] = dst[i] + _matrices[i][j];}}}if (!update){break;}}//检查负权回路//再次更新一轮,检查是否能更新,如果还能更新,则存在负权回路。//如果没有更新,则为false,即bool is_existed = false;for (size_t i = 0; i < n; i++){for (size_t j = 0; j < n; j++){//边存在,并且 s->i + i->j < s->j if (_matrices[i][j] != W_MAX && dst[i] + _matrices[i][j] < dst[j]){is_existed = true;}}}if (is_existed){return false;}return true;
}
- 测试用例:
void TestGraphBellmanFord(){const char* str = "syztx";Graph<char, int, INT_MAX, true> g(str, strlen(str));g.AddEdge('s', 't', 6);g.AddEdge('s', 'y', 7);g.AddEdge('y', 'z', 9);g.AddEdge('y', 'x', -3);g.AddEdge('z', 's', 2);g.AddEdge('z', 'x', 7);g.AddEdge('t', 'x', 5);g.AddEdge('t', 'y', 8);g.AddEdge('t', 'z', -4);g.AddEdge('x', 't', -2);vector<int> dist;vector<int> parentPath;if (g.BellmanFord('s', dist, parentPath)){g.Print();g.PrinrtShotPath('s', dist, parentPath);}else{cout << "存在负权回路" << endl;}}
- 运行结果:
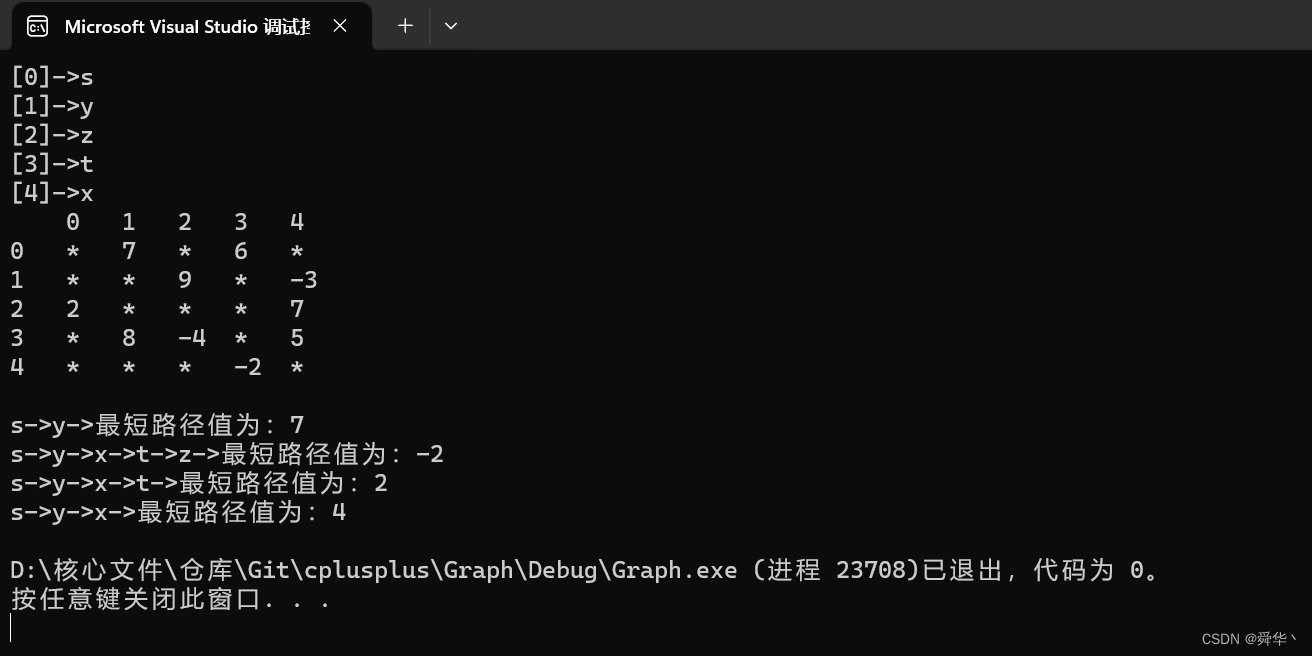
- 图解:
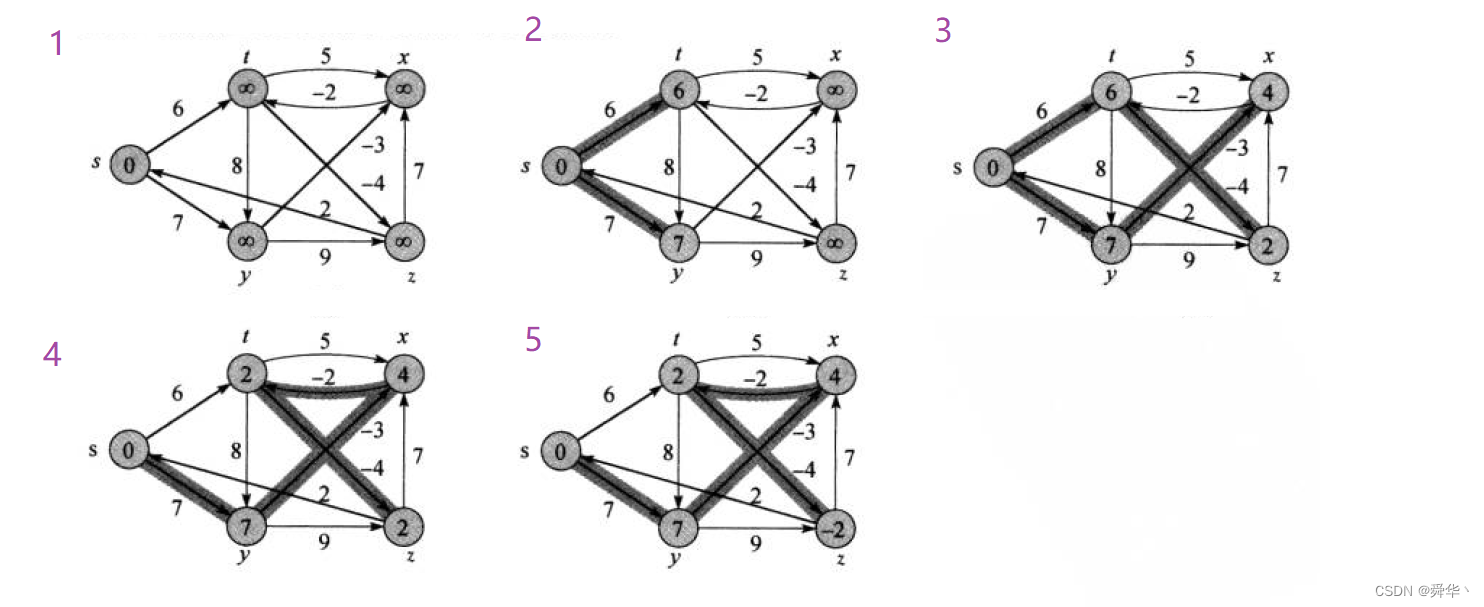
-
说明:暴力更新,调试着看数据的变化效果更好。
-
测试用例2:
void TestGraphBellmanFord(){// 微调图结构,带有负权回路的测试const char* str = "syztx";Graph<char, int, INT_MAX, true> g(str, strlen(str));g.AddEdge('s', 't', 6);g.AddEdge('s', 'y', 7);g.AddEdge('y', 'x', -3);g.AddEdge('y', 'z', 9);g.AddEdge('y', 'x', -3);g.AddEdge('z', 's', -2);//更改此处见效更明显。g.AddEdge('z', 'x', 7);g.AddEdge('t', 'x', 5);g.AddEdge('t', 'y', 8);g.AddEdge('t', 'z', -4);g.AddEdge('x', 't', -2);vector<int> dist;vector<int> parentPath;if (g.BellmanFord('s', dist, parentPath)){g.PrinrtShotPath('s', dist, parentPath);}else{cout << "存在负权回路" << endl;}}
- 运行结果:
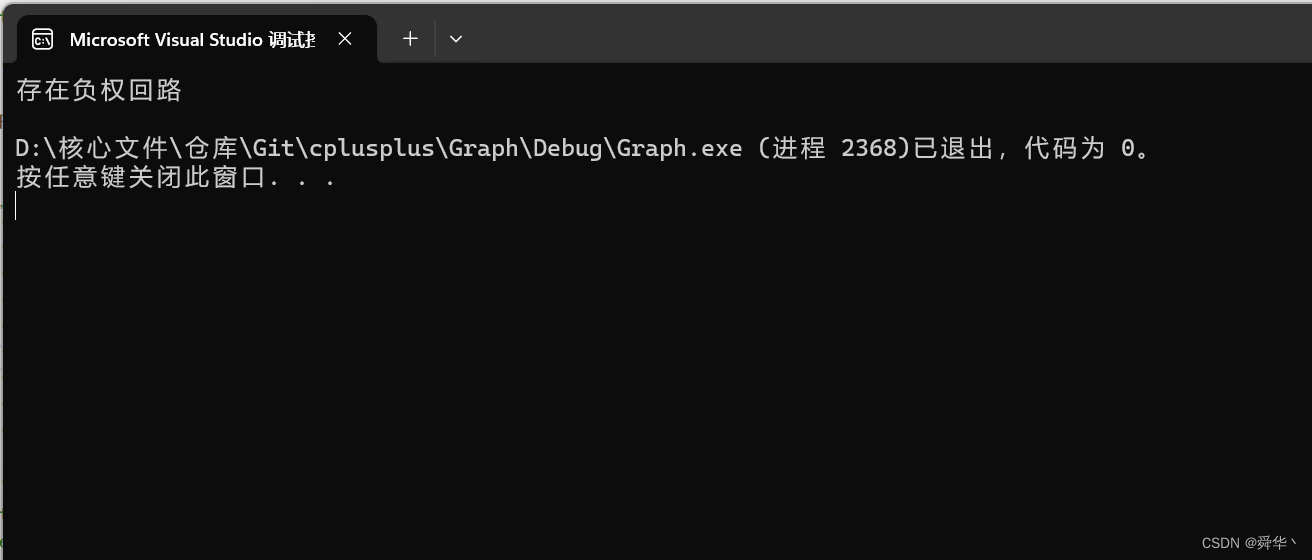
- 图解:
说明:暴力循环完之后,再更新一次又会引起其它变小,此种情况只会越更新越小,求不出最小路径!
5.3floyd warshall算法
-
用处:多源最短路径的负权值(不带负权回路)的图
-
算法思想(dp):
- 拆分子问题:分为两种情况
- 所有的边经过点K.
- 所有的边不经过点K.
- 这里的K可能是所有的顶点。
- 因此求前两种情况的所有情况的最小值即可。
图解:

- 实现代码:
void FloydWarshall(vector<vector<W>>& vvdst,
vector<vector<int>>& vvpPath)
{size_t n = _vertexs.size();//初始化dst与pPathvvdst.resize(n);vvpPath.resize(n);for (size_t i = 0; i < n; i++){vvdst[i].resize(n, W_MAX);vvpPath[i].resize(n, -1);}//再对边进行初始化,即将i直接到j的边先放在des数组中for (size_t i = 0; i < n; i++){for (size_t j = 0; j < n; j++){if (_matrices[i][j] != W_MAX){vvdst[i][j] = _matrices[i][j];vvpPath[i][j] = i;}if (i == j){//与此同时由于是距离,所以i == j 即 i->i 的距离为0vvdst[i][j] = 0;}}}for (size_t k = 0; k < n; k++){//其中暴力选择k做为中间的边,分析是选择还是不选for (size_t i = 0; i < n; i++){//从中进行选则两端的边for (size_t j = 0; j < n; j++){//选择k作为中间的边,如果i->k,k->j < i->j//即分析是取k小还是不取k小,这里的k采用暴力枚举的方式。if (vvdst[i][k] != W_MAX && vvdst[k][j] != W_MAX&& vvdst[i][k] + vvdst[k][j] < vvdst[i][j]){//则需要更新dst[i][j]的父路径以及权值vvdst[i][j] = vvdst[i][k] + vvdst[k][j];/*i->k 更新 k->j,应为pPath[k][j]如果k->j中间没有其他结点,则说明 pPath[k][j] == k如果k->……->x->j中间经过了其它结点,则 pPath[k][j]==x*/vvpPath[i][j] = vvpPath[k][j];}}}}//此处我们打印出权值和路径的矩阵cout << " ";for (size_t i = 0; i < n; i++){printf("%-3d", i);}cout << endl;//1.权值矩阵for (size_t i = 0; i < n; i++){printf("%-3d", i);for (size_t j = 0; j < n; j++){if (vvdst[i][j] == W_MAX){printf("%-3c", '*');}else{printf("%-3d", vvdst[i][j]);}}cout << endl;}printf("=============================================\n");//2.路径矩阵cout << " ";for (size_t i = 0; i < n; i++){cout << i << " ";}cout << endl;for (size_t i = 0; i < n; i++){cout << i << " ";for (size_t j = 0; j < n; j++){cout << vvpPath[i][j] << " ";}cout << endl;}
}
- 测试用例:
void TestFloydWarShall(){const char* str = "12345";Graph<char, int, INT_MAX, true> g(str, strlen(str));g.AddEdge('1', '2', 3);g.AddEdge('1', '3', 8);g.AddEdge('1', '5', -4);g.AddEdge('2', '4', 1);g.AddEdge('2', '5', 7);g.AddEdge('3', '2', 4);g.AddEdge('4', '1', 2);g.AddEdge('4', '3', -5);g.AddEdge('5', '4', 6);vector<vector<int>> vvDist;vector<vector<int>> vvParentPath;g.FloydWarshall(vvDist, vvParentPath);// 打印任意两点之间的最短路径for (size_t i = 0; i < strlen(str); ++i){g.PrinrtShotPath(str[i], vvDist[i], vvParentPath[i]);cout << endl;}}
运行结果:

- 图解:
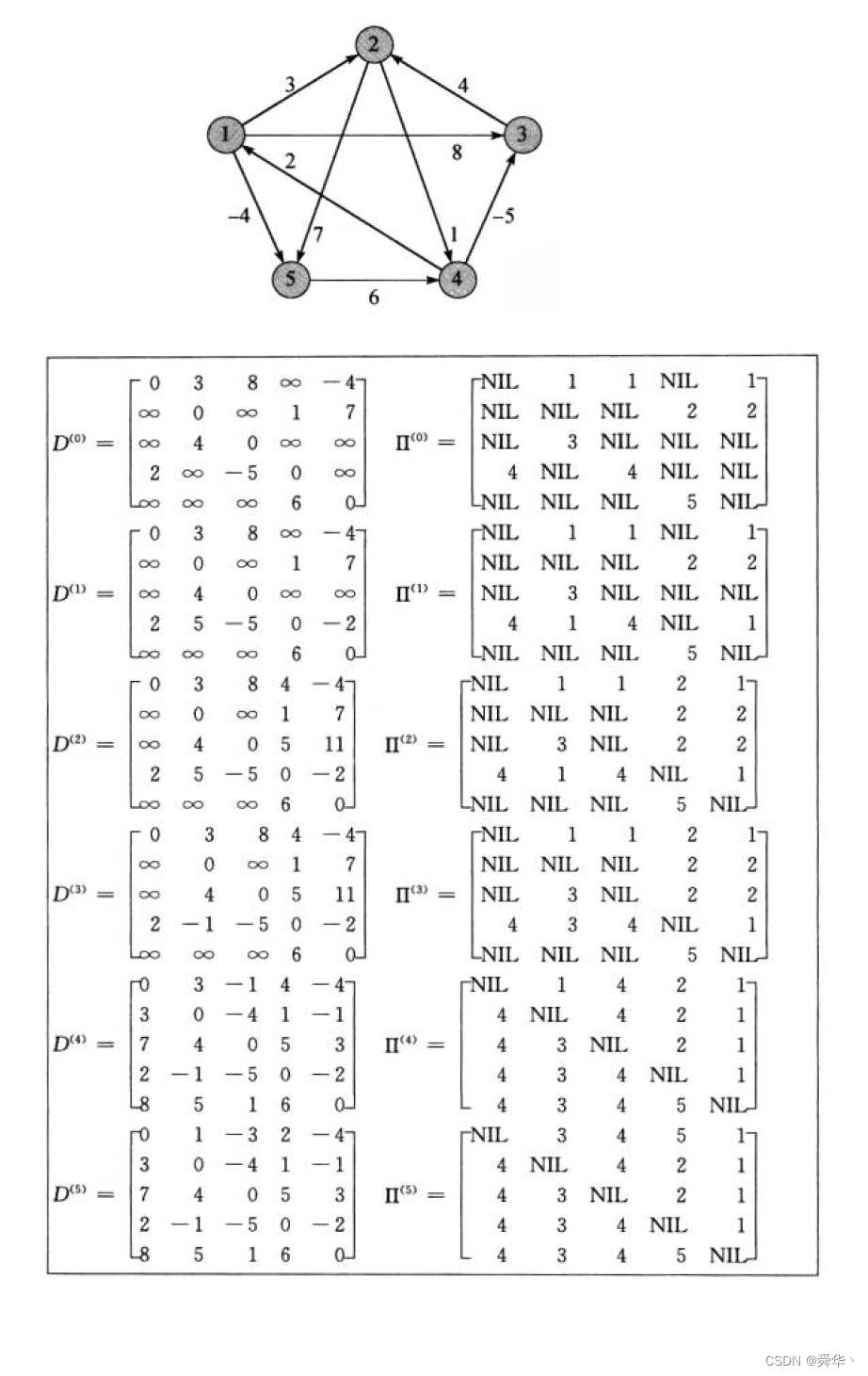
说明:这里II的矩阵表示的数字是
真实下标对应的数字,我们这里打印的父路径的矩阵表示的数字是下标,因此还需要对不为-1的数加上1才对的上。
总结
- 并查集的原理和基本实现。
- 图论的基本概念,存储结构(邻接表和邻接矩阵),遍历方式(广度优先和深度优先),最小生成树的两个算法,最短路径的三个算法。
- 并查集是一个较为简单的数据结构,而图论的表示形式是较为抽象的,需要我们将实际的例子抽象处理,因此不太好理解,关键在于多调试,多画图。
尾序
我是舜华,期待与你的下一次相遇!
相关文章:

【数据结构】图论与并查集
一、并查集 1.原理 简单的讲并查集,就是查询两个个元素,是否在一个集合当中,这里的集合用树的形式进行表示。并查集的本质就是森林, 即多棵树。 我们再来简单的举个例子: 假设此时的你是大一新生,刚进入大学,肯定是…...

冲刺港股IPO,速腾聚创「承压」
对于「光鲜」的激光雷达公司来说,当下最难的问题是:如何说服投资者相信,前装市场能够按照预期定点订单兑现。 今年,作为国内高阶智驾头部车企之一的华为,在陆续推出的新车型上开始「降本」。其中,问界智驾版…...
Linux基础知识点(五-信号)
一、信号的基本概念 1.1 信号的概念 信号(signal),又称为软中断信号,用于通知进程发生了异步事件,它是Linux系统响应某些条件而产生的一个事件,它是在软件层次上对中断机制的一种模拟,是一种异…...
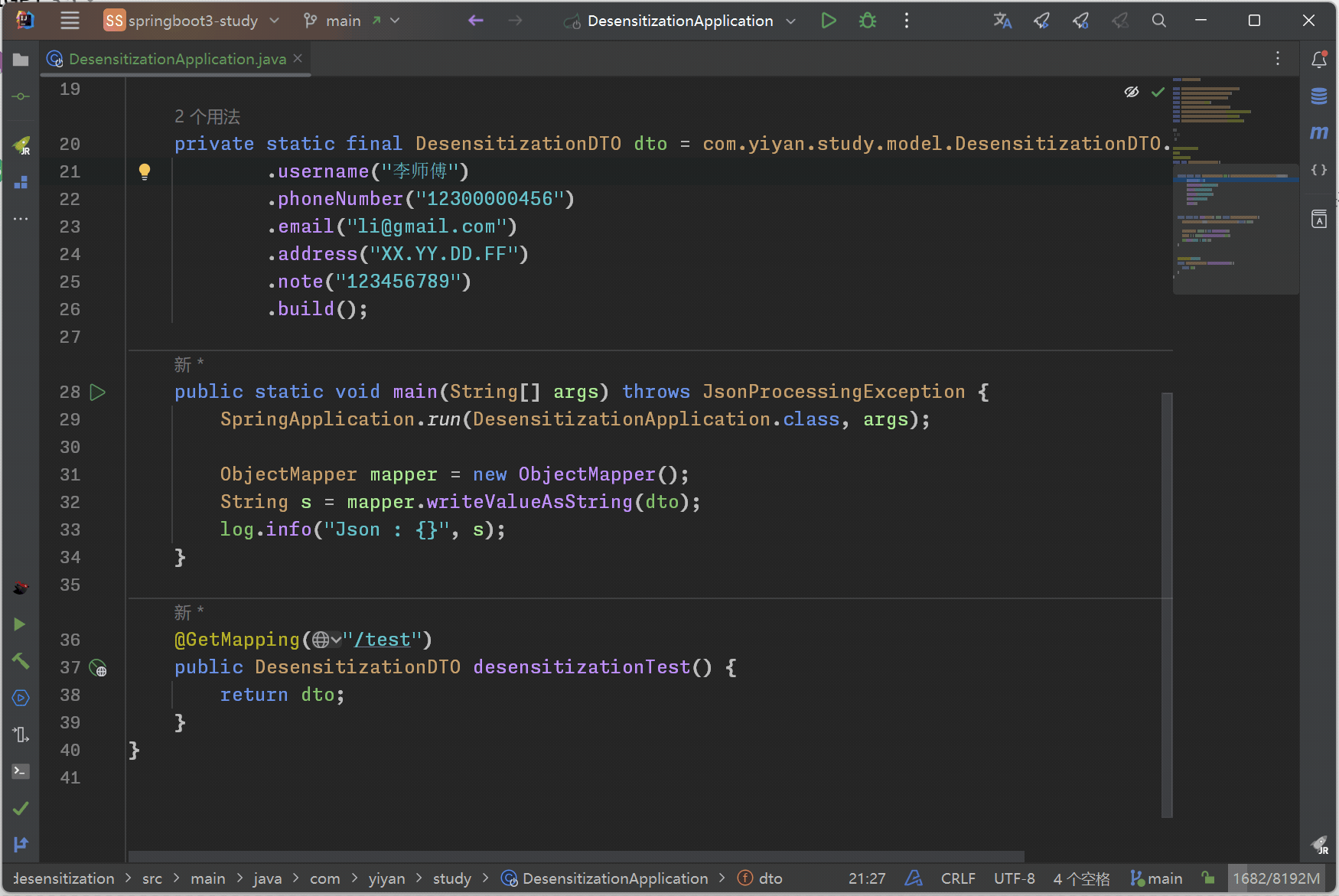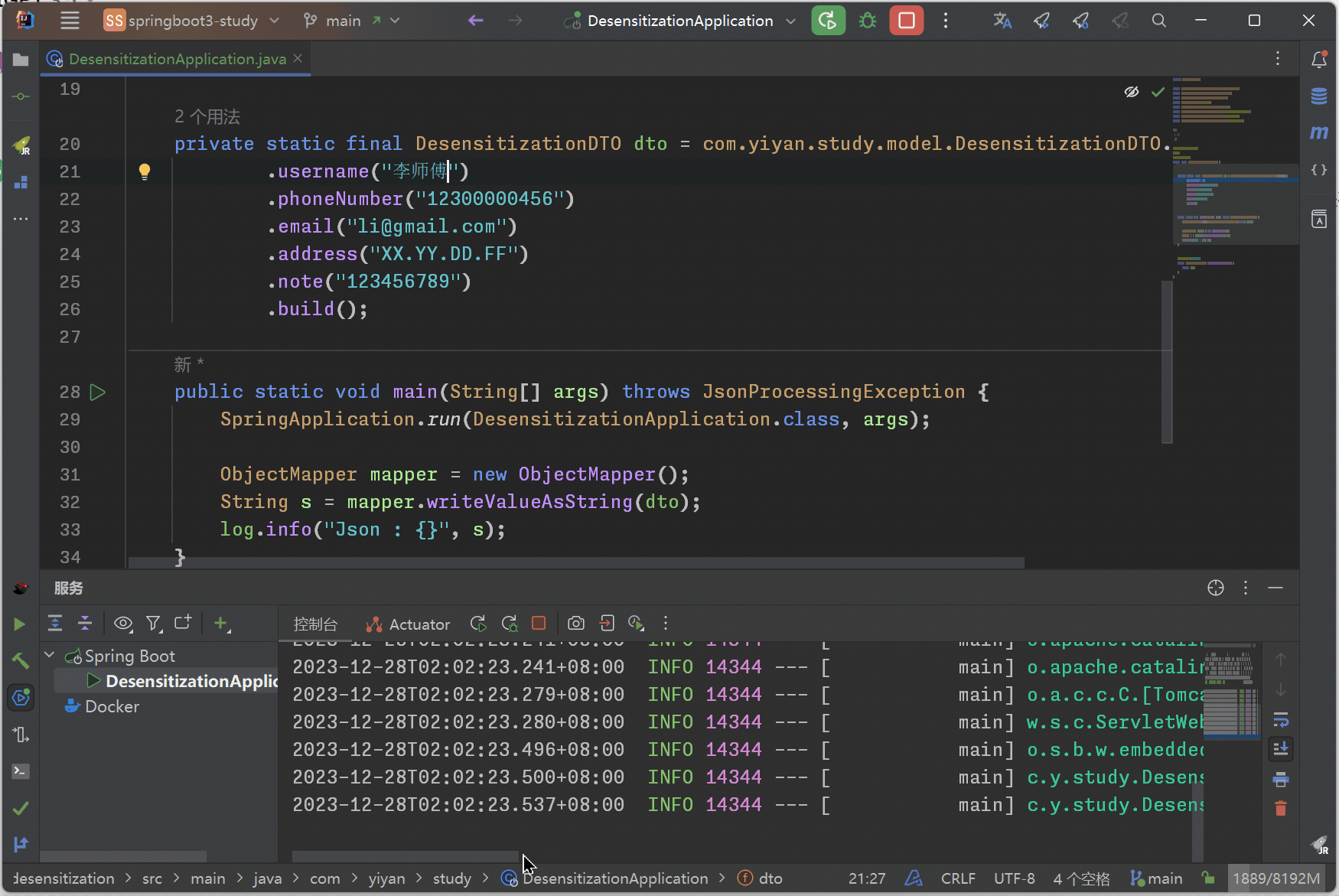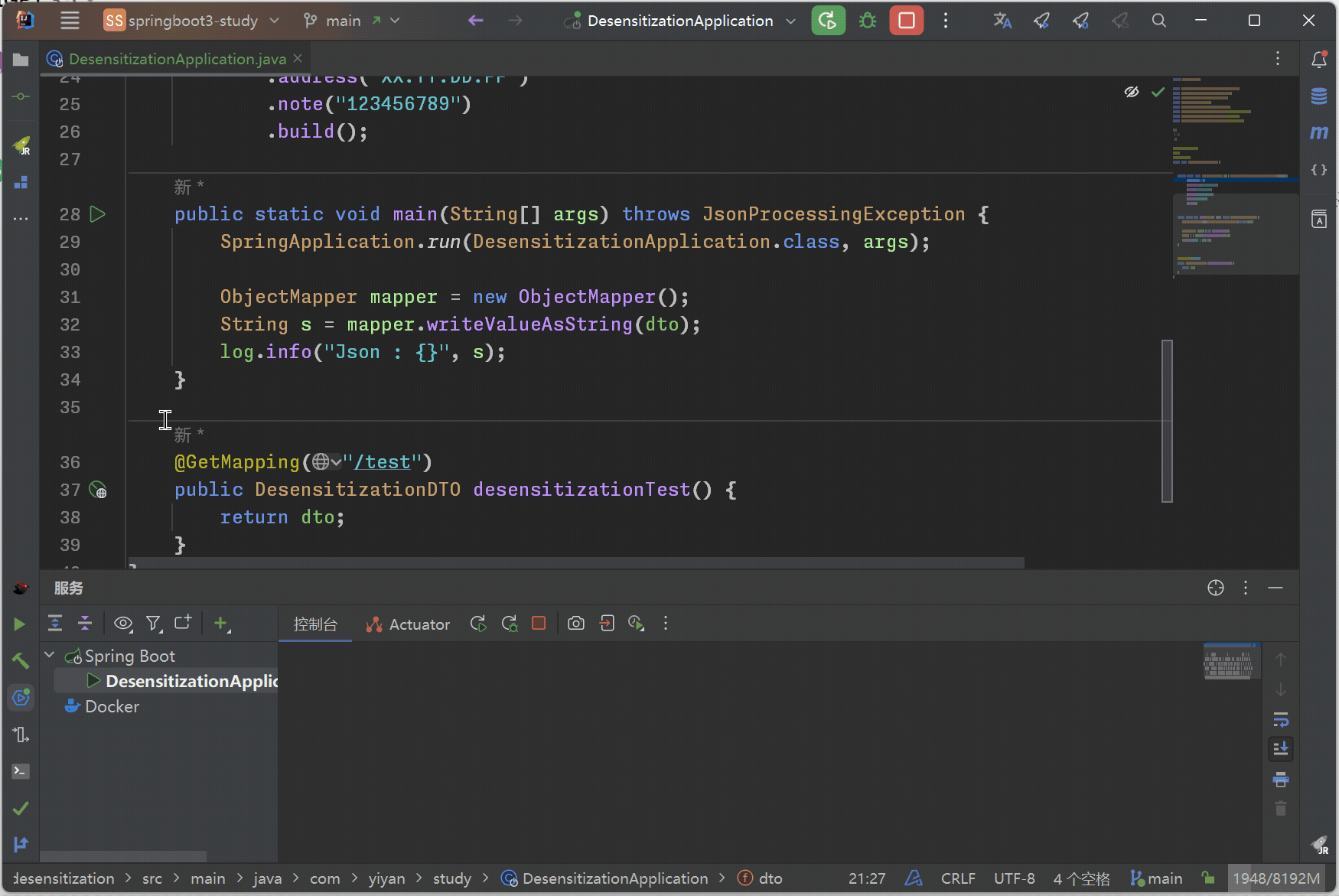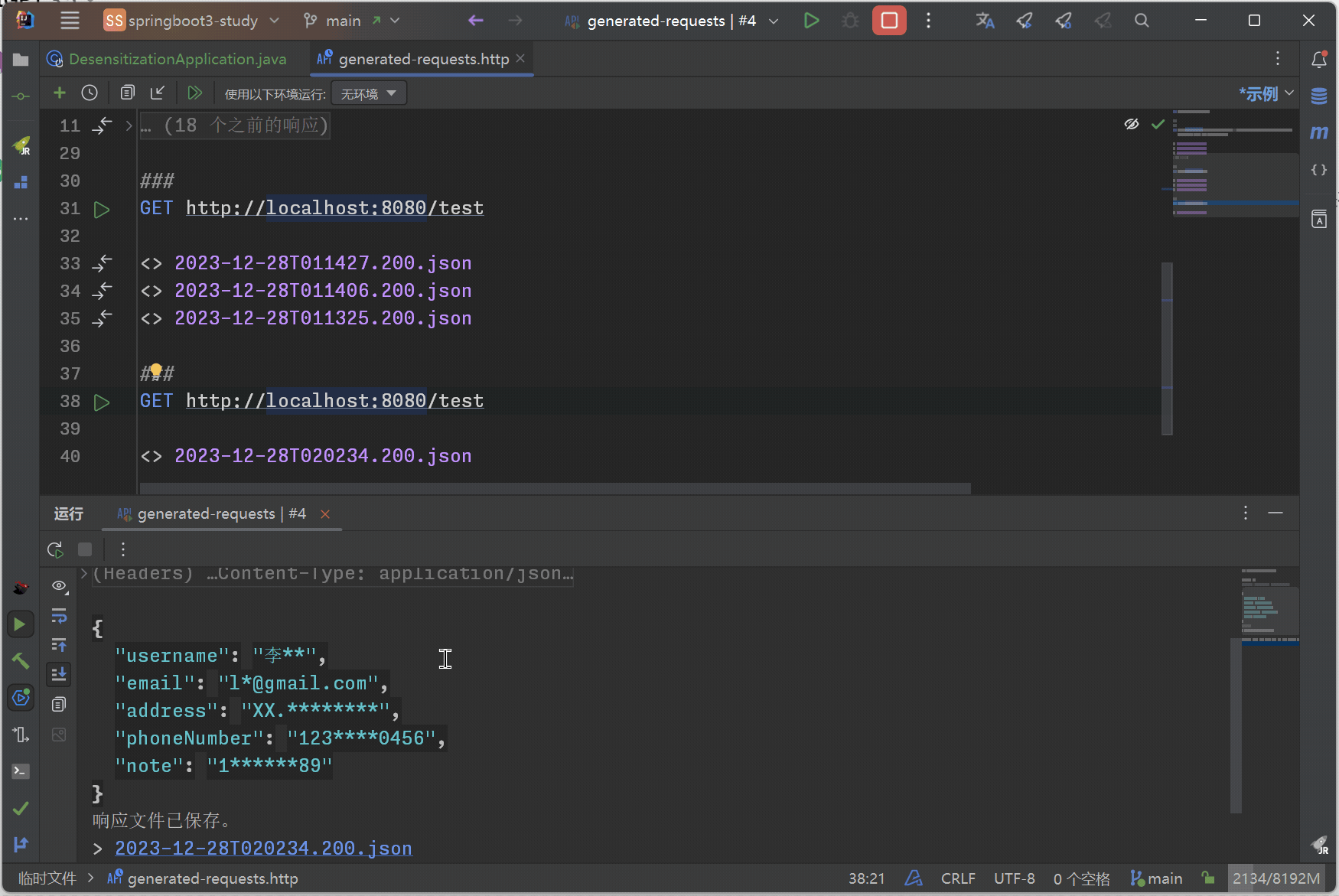
SpringBoot 一个注解实现数据脱敏
什么是数据脱敏 数据脱敏是指对某些敏感信息,例如姓名、身份证号码、手机号、固定电话、银行卡号、邮箱等个人信息,通过脱敏算法进行数据变形,以保护敏感隐私数据。 数据脱敏通常涉及以下几种主要方法: 替换: 将原始…...

记录:开始学习网络安全
本文持续更新学习进度 背景 在私企干了5年虚拟化、云原生相关的运维,学到了很多,但不成体系。老板是清华毕业法国留学在德勤干过,最后回国创业的野路子。我工作是为了更好的生活,我挺担心老板因为家庭变故或者炒个原油宝&#x…...

C语言—第1次作业:编译与连接基础知识
常做练习巩固知识 本次作业答案链接如下: 答案解析——C语言—第1次作业:编译与连接基础知识 1.字符串的结束标志是:( ) A.是0 B.是EOF C. 是\0 D.是空格 2.关于C语言关键字说法正确的是:( ) A.关…...

not attached to window manager问题解决
关于出现这个问题,一般是因为Activity已经在finish了,但是还在dialog.show(),或者dialog.dismiss().导致window manager无法管理dialog。解决办法如下: /** * 20210913 安全关闭对话框 . * 避免报:not attac…...
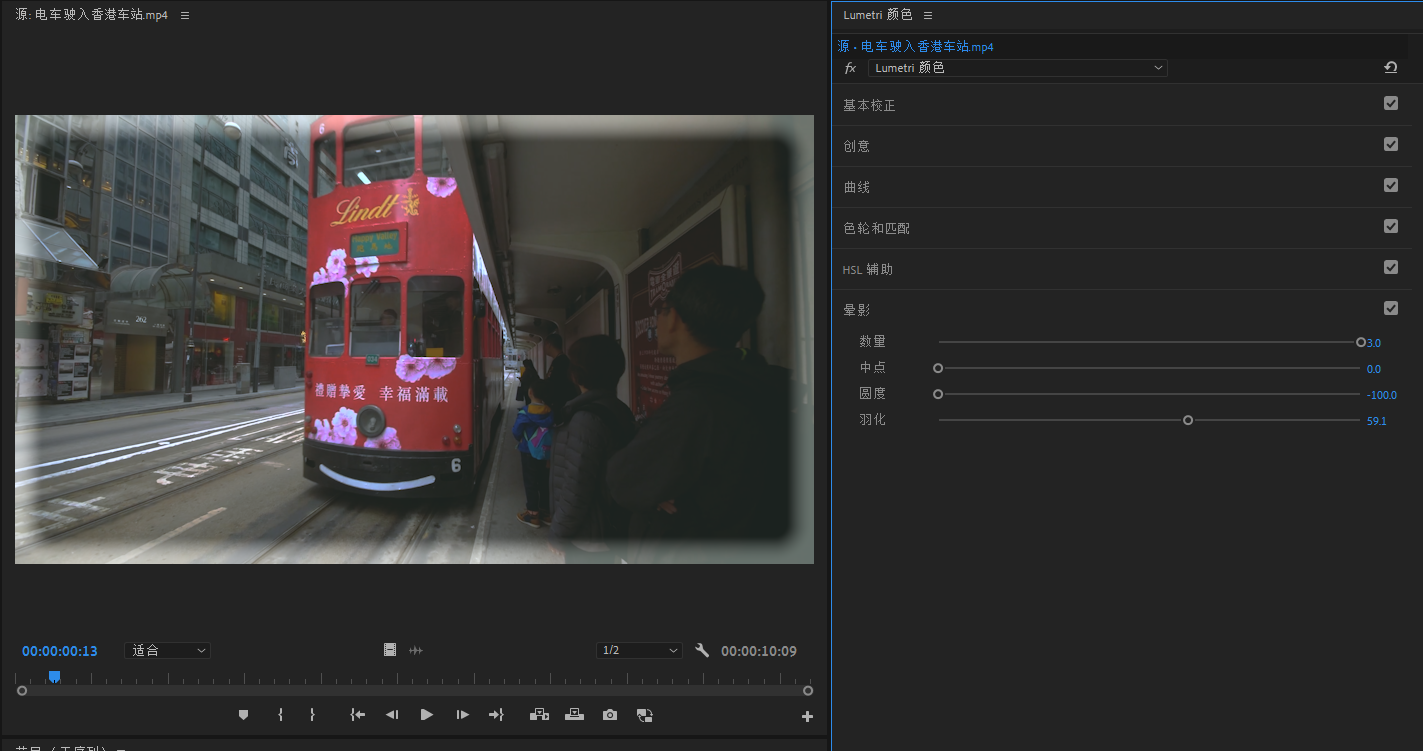
影视后期: PR调色处理,调色工具面板介绍
写在前面 整理一些影视后期的相关笔记博文为 Pr 调色处理,涉及调色工具面板简单认知包括 lumetri 颜色和范围面板理解不足小伙伴帮忙指正 元旦快乐哦 _ 名词解释 饱和度 是指色彩的鲜艳程度,也被称为色彩的纯度。具体来说,它表示色相中灰色…...
详解(上))
ARM AArch64的虚拟化(virtualization)详解(上)
目录 一、概述 开始之前 二、虚拟化介绍 为什么虚拟化很重要...

计算机组成原理知识总结
目录 第一章、计算机系统概述知识框架:1.冯诺依曼机和存储程序的概念?2.计算机的工作过程?3.在计算机系统结构中,什么是编译?什么是解释?4.描述一下指令执行过程?1) 取指令: PC 一&g…...
 解决springboot3.2找不到资源无法抛出404错误的问题)
springboot学习(八十五) 解决springboot3.2找不到资源无法抛出404错误的问题
前言 springboot3.2以下可以定义ErrorPageRegistrar将404错误转发到一个接口地址,但升级到springboot3.2(spring6.1)后,该配置不生效,抛出了500错误。 以前的错误页面处理如下: ConditionalOnClass(ErrorPageRegist…...
OpenHarmony 应用通用签名
一.背景 由于hap包需要经过签名才能安装到设备上,在DevEco Studio可以进行自动签名,但是自动签名只能安装在当前的设备上,在其他设备上不能安装,所以我们需要进行通用的手动签名,手动签名HarmonyOS和OpenHarmony流程是…...
Redis:原理+项目实战——Redis实战1(session实现短信登录(并剖析问题))
👨🎓作者简介:一位大四、研0学生,正在努力准备大四暑假的实习 🌌上期文章:Redis:原理速成项目实战——Redis的Java客户端 📚订阅专栏:Redis速成 希望文章对你们有所帮助…...
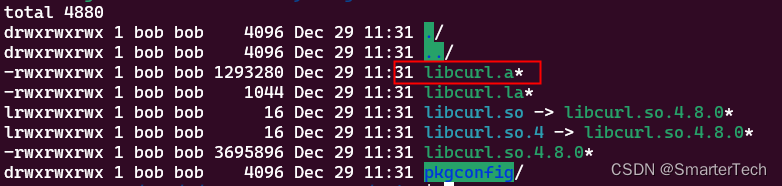
交叉编译aarch64架构支持openssl的curl、libcurl
本文档旨在指导读者在x86_64平台上交叉编译curl和openssl库以支持aarch64架构。在开始之前,请确保您的系统环境已正确配置。 1. 系统环境准备 系统是基于Ubuntu 20.04 LTS,高版本可能会有问题。首页,安装必要的开发工具和库文件。打开终端并…...
扩展名是.KEY的文件可能有不同的存在,打开方式也因此不同
本文解释了使用KEY文件扩展名的所有不同格式,以及如何在可能的情况下打开和转换每种格式。 KEY文件的定义 KEY文件扩展名可能是用于注册软件程序的纯文本或加密的通用许可证密钥文件。不同的应用程序使用不同的KEY文件来注册各自的软件,并证明用户是合…...
软件工程总复习笔记
软件工程课程复习提纲 文章目录 软件工程课程复习提纲一、基本知识点1. 软件工程的概念及目标2. 软件危机的概念及典型表现3. 瀑布模型的概念及特点4. 快速原型模型的特点5. 螺旋模型的基本思想6. 软件生命周期的概念及划分为哪几个阶段7. 软件需求的定义8. 常见的软件需求获取…...

蓝桥杯-每日刷题-030
打印等边三角形 一、题目要求 题目描述 输出等边三角形:输入n值,输出高度为n的等边三角形。输入格式 输入存在多组测试数据。对于每组测试数据输入一个正整数n(1<n<100)。输出格式 对于每组测试数据输出对应的等边三角形。每组测试数据最后输出一…...

AI赋能游戏开发,如何更好地处理随之而来的海量数据,更好地利用开发游戏?
人工智能(AI)正在改变我们所知的游戏行业。它为3A工作室、独立开发者和业余爱好者提供了工具,让他们能够更轻松地创建以前需要大量时间和资源的项目。尤其是,虚幻引擎的AI工具已经取得了显著的进步。 虚幻引擎AI拥有专门用于游戏…...

Serverless架构学习路线及平台对比
在云计算领域,Serverless架构已经成为了一个重要的趋势。本文将为你提供一条清晰的Serverless架构学习路线,帮助你系统地掌握这个领域的知识,并对比国内外的Serverless平台的优缺点。 一、基础理论学习 首先,我们需要理解Server…...

解决ROS含动态参数的Config文件无法正确识别的错误
问题描述 功能包名为paddle_detection 在工作空间下, 通过catkin_make可以正常通过编译且执行无异常, 可以通过bloom-generate rosdebian生成依赖 但是在将其打包成deb包的过程中fakeroot debian/rules binary报错 fatal error: paddle_detection/paddle_detectionConfig.…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

如何把工业通信协议转换成http websocket
1.现状 工业通信协议多数工作在边缘设备上,比如:PLC、IOT盒子等。上层业务系统需要根据不同的工业协议做对应开发,当设备上用的是modbus从站时,采集设备数据需要开发modbus主站;当设备上用的是西门子PN协议时…...

高效的后台管理系统——可进行二次开发
随着互联网技术的迅猛发展,企业的数字化管理变得愈加重要。后台管理系统作为数据存储与业务管理的核心,成为了现代企业不可或缺的一部分。今天我们要介绍的是一款名为 若依后台管理框架 的系统,它不仅支持跨平台应用,还能提供丰富…...