【数据结构】二叉搜索(查找/排序)树
一、二叉搜索树基本概念
1、定义
二叉搜索树,又称为二叉排序树,二叉查找树,它满足如下四点性质:
1)空树是二叉搜索树;
2)若它的左子树不为空,则左子树上所有结点的值均小于它根结点的值;
3)若它的右子树不为空,则右子树上所有结点的值均大于它根结点的值;
4)它的左右子树均为二叉搜索树;
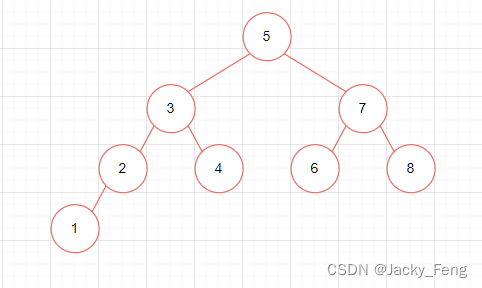
如上图所示:二叉搜索树的任何一棵子树,它的根结点的值一定大于左子树所有结点的值,且一定小于右子树所有结点的值。如果对二叉搜索树进行中序遍历,我们可以发现,得到的序列是一个递增序列,上述的遍历结果为[1,2,3,4,5,6,7,8]。
如果要查找4,只需要从根结点比较查找3次就能找到,可以显著提高搜索的速度。
二、二叉搜索树基础操作
1、查找算法
(1)查找原理
在二叉搜索树中查找某个数是否存在,存在返回 true,不存在返回 false。
对于要查找的数 val ,从根结点出发,总共四种情况依次判断:
1)若二叉搜索树为空树,直接返回 false;
2) val 的值 等于 树根结点的值,则直接返回 true;
3) val 的值 小于 树根结点的值,说明 val 对应的结点不在根结点,也不在右子树上,需要在左子树上查找,递归返回左子树的查找结果;
4) val 的值 大于 树根结点的值,说明 val 对应的结点不在根结点,也不在左子树上,需要在右子树上查找,递归返回右子树的查找结果;
(2)查找算法源码
① 结点源码
struct TreeNode {int val;struct TreeNode *left;struct TreeNode *right;TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}};② 查找算法源码 (深度优先,递归查找)
bool BSTFind(TreeNode* root, int val)
{if (root == nullptr) {return false;}if (root->val == val) {return true;}if (val < root->val) {return BSTFind(root->left, val);}else {return BSTFind(root->right, val);}
}2、插入算法
(1)插入原理
将给定的值 val 生成结点后,插入到树上的某个位置,并且保持这棵树还是二叉搜索树。对于要插入的值 val ,从根结点出发,总共四种情况依次判断:
1)若为空树,则创建一个值为 val 的结点并且返回根结点;
2) val 的值 等于 树根结点的值,无须执行插入,直接返回根结点;
3) val 的值 小于 树根结点的值,那么插入位置一定在 左子树,递归执行插入左子树的过程,并且返回插入结果作为新的左子树;
4) val 的值 大于 树根结点的值,那么插入位置一定在 右子树,递归执行插入右子树的过程,并且返回插入结果作为新的右子树;
(2) 插入源码
TreeNode* BSTInsert(TreeNode* root, int val) {if (root == nullptr) {root = new TreeNode(val);return root;}if (val == root->val) {return root;}if (val < root->val) {root->left = BSTInsert(root->left, val);}else {root->right = BSTInsert(root->right, val);}return root;
}3、删除算法
(1)删除原理
删除值为 val 结点,从根结点出发,总共四种情况依次判断:
1)空树,不存在结点直接返回空树;
2) val 的值 小于 树根结点的值,则需要删除的结点一定不在右子树上,递归调用删除左子树的对应结点;
3) val 的值 大于 树根结点的值,则需要删除的结点一定不在左子树上,递归调用删除右子树的对应结点;
4) val 的值 等于 树根结点的值,相当于是要删除根结点,这时候又要分三种情况:
- 当前树只有左子树,则直接将左子树返回,并且释放当前树根结点的空间;
- 当前树只有右子树,则直接将右子树返回,并且释放当前树根结点的空间;
- 当左右子树都存在时,需要在右子树上找到一个值最小的结点,替换新的树根,而其它结点组成的树作为它的子树;
(2)删除源码
由上述删除算法原理可知,删除结点之前可能还需要找最小结点,所以需要定义查找最小结点接口。
int BSTFindMin(TreeNode* root) {if (root->left)return BSTFindMin(root->left); return root->val;
}查找根为 root ,值最小的那个结点的值,根据二叉搜索树的性质,如果左子树存在,则必然存在更小的值,递归搜索左子树,且最小值结点为叶子结点;如果左子树不存在,则根结点的值必然最小,直接返回。
删除根结点,并返回新根结点
//删除根结点并返回新根结点
TreeNode* Delete(TreeNode* root) {TreeNode* delNode, * retNode;if (root->left == nullptr) {delNode = root;retNode = root->right;delete delNode;delNode = nullptr;}else if (root->right == nullptr) {delNode = root;retNode = root->left;delete delNode;delNode = nullptr;}else {retNode = BSTFindMin(root->right);retNode->left = root->left;retNode->right = root->right;delete root;root = nullptr;}return retNode;
}- 如果左子树为空,则用右子树做为新的树根;
- 如果右子树为空,则用左子树作为新的树根;
- 否则,当左右子树都为非空时,利用 BSTFindMin ,从右子树上找出最小的结点,作为新的根。
删除指定值的结点
//删除指定结点
TreeNode* BSTDelete(TreeNode* root, int val) {if (nullptr == root) {return nullptr; }if (val == root->val) {return Delete(root); }else if (val < root->val) {root->left = BSTDelete(root->left, val); }else if (val > root->val) {root->right = BSTDelete(root->right, val); }return root;
}- 如果为空树,则直接返回空结点;
- 如果需要删除的结点的值 等于 树根结点的值,则直接调用接口 Delete ;
- 如果需要删除的结点的值 小于 树根结点的值,则需要删除的结点必定在左子树上,递归调用左子树的删除,并且将返回值作为新的左子树的根结点;
- 如果需要删除的结点的值 大于 树根结点的值,则需要删除的结点必定在右子树上,递归调用右子树的删除,并且将返回值作为新的右子树的根结点;
- 返回当前树的根结点;
相关文章:

【数据结构】二叉搜索(查找/排序)树
一、二叉搜索树基本概念 1、定义 二叉搜索树,又称为二叉排序树,二叉查找树,它满足如下四点性质: 1)空树是二叉搜索树; 2)若它的左子树不为空,则左子树上所有结点的值均小于它根结…...
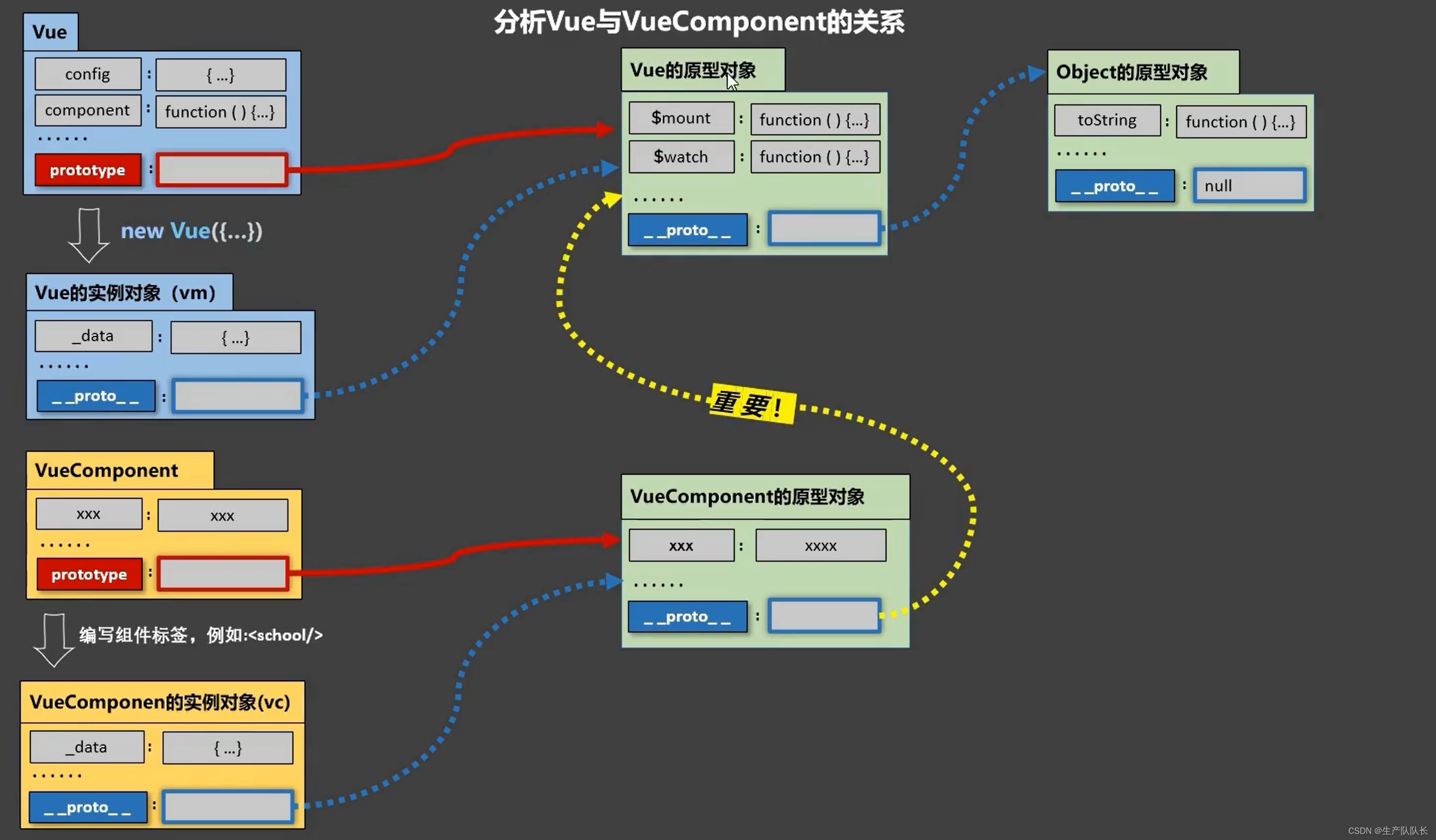
Vue:Vue与VueComponent的关系图
1.一个重要的内置关系:VueComponent.prototype.proto Vue.prototype 2.为什么要有这个关系:让组件实例对象(vc)可以访问到 Vue原型上的属性、方法。 案例证明: <!DOCTYPE html> <html lang"en"&…...

Elasticsearch8集群部署
转载说明:如果您喜欢这篇文章并打算转载它,请私信作者取得授权。感谢您喜爱本文,请文明转载,谢谢。 本文记录在3台服务器上离线搭建es8.7.1版本集群。 1. 修改系统配置 1.1 hosts配置 在三台es节点服务器加入hostname解析&…...

【小白专用】c# 如何获取项目的根目录
1、取得控制台应用程序的根目录方法 方法1、Environment.CurrentDirectory 取得或设置当前工作目录的完整限定路径 方法2、AppDomain.CurrentDomain.BaseDirectory 获取基目录,它由程序集冲突解决程序用来探测程序集 2、取得Web应用程序的根目录方法 方法1、HttpRun…...

【PXIE301-208】基于PXIE总线架构的Serial RapidIO总线通讯协议仿真卡
板卡概述 PXIE301-208是一款基于3U PXIE总线架构的Serial RapidIO总线通讯协议仿真卡。该板卡采用Xilinx的高性能Kintex系列FPGA作为主处理器,实现各个接口之间的数据互联、处理以及实时信号处理。板卡支持4路SFP光纤接口,支持一个PCIe x8主机接口&…...

软件测试/测试开发丨Windows系统chromedriver安装与环境变量配置
一、selenium 环境配置 1、chrome 浏览器的安装与配置 目前比较常用的浏览器是 Google Chrome 浏览器,所以本教程以 chrome 为主,后面简介一下其他浏览器的环境配置。 (1)chrome 下载: www.google.cn/chrome/ (2&a…...

【vim 学习系列文章 3.1 -- vim 删除 ^M】
请阅读【嵌入式开发学习必备专栏 之 VIM 专栏】 文章目录 ^M 来源^M 删除 ^M 来源 在 Vim 中打开文件时,您可能会遇到行尾的 ^M 字符,这通常是因为文件使用了 Windows 风格的回车换行符(CRLF),而不是 Unix/Linux 风格…...

深入理解 C# 中的字符串比较:String.CompareTo vs String.Equals
深入理解 C# 中的字符串比较:String.CompareTo vs String.Equals 在处理字符串时,了解如何正确比较它们对于编写清晰、有效和可靠的 C# 程序至关重要。本文将深入探讨 C# 中的两个常用字符串比较方法:String.CompareTo 和 String.Equals&…...
DevOps持续交付之容器化CICD流水线
DevOps持续交付 随着DevOps⼤规模化的落地和应⽤,持续集成以及持续交付已经是⼀种常态的。CI指的是持续集成,使⽤的开源⼯具是Jenkins,CD指的是持续交付和持续部署,⼀个完整的软件开发⽣命周期为: 主要流程可以具体为: 构建阶段…...

Linux/Unix/国产化操作系统常用命令(二)
目录 后CentOS时代国产化操作系统国产化操作系统有哪些常用Linux命令关于Linux的LOGO 后CentOS时代 在CentOS 8发布后,就有了一些变化和趋势,可以说是进入了"后CentOS时代"。这个时代主要表现在以下几个方面: CentOS Stream的引入…...

基于SpringBoot的智慧生活商城系统
文章目录 项目介绍主要功能截图:部分代码展示设计总结项目获取方式🍅 作者主页:超级无敌暴龙战士塔塔开 🍅 简介:Java领域优质创作者🏆、 简历模板、学习资料、面试题库【关注我,都给你】 🍅文末获取源码联系🍅 项目介绍 基于SpringBoot的智慧生活商城系统,java…...
Vue框架引入Axios
首先已经创建好了 Vue 框架,安装好了 node.js。 没有完成的可按照此博客搭建:搭建Vue项目 之后打开终端,使用命令。 1、命令安装 axios 和 vue-axios npm install axios --save npm install vue-axios --save2、package.json 查看版本 在 p…...

EasyExcel 通过模板 导入、导出、下载模板
EasyExcel 通过模板 导入、导出、下载模板 import lombok.AllArgsConstructor; import lombok.Builder; import lombok.Data; import lombok.NoArgsConstructor;import javax.validation.constraints.NotBlank; import javax.validation.constraints.Pattern; import java.io.…...
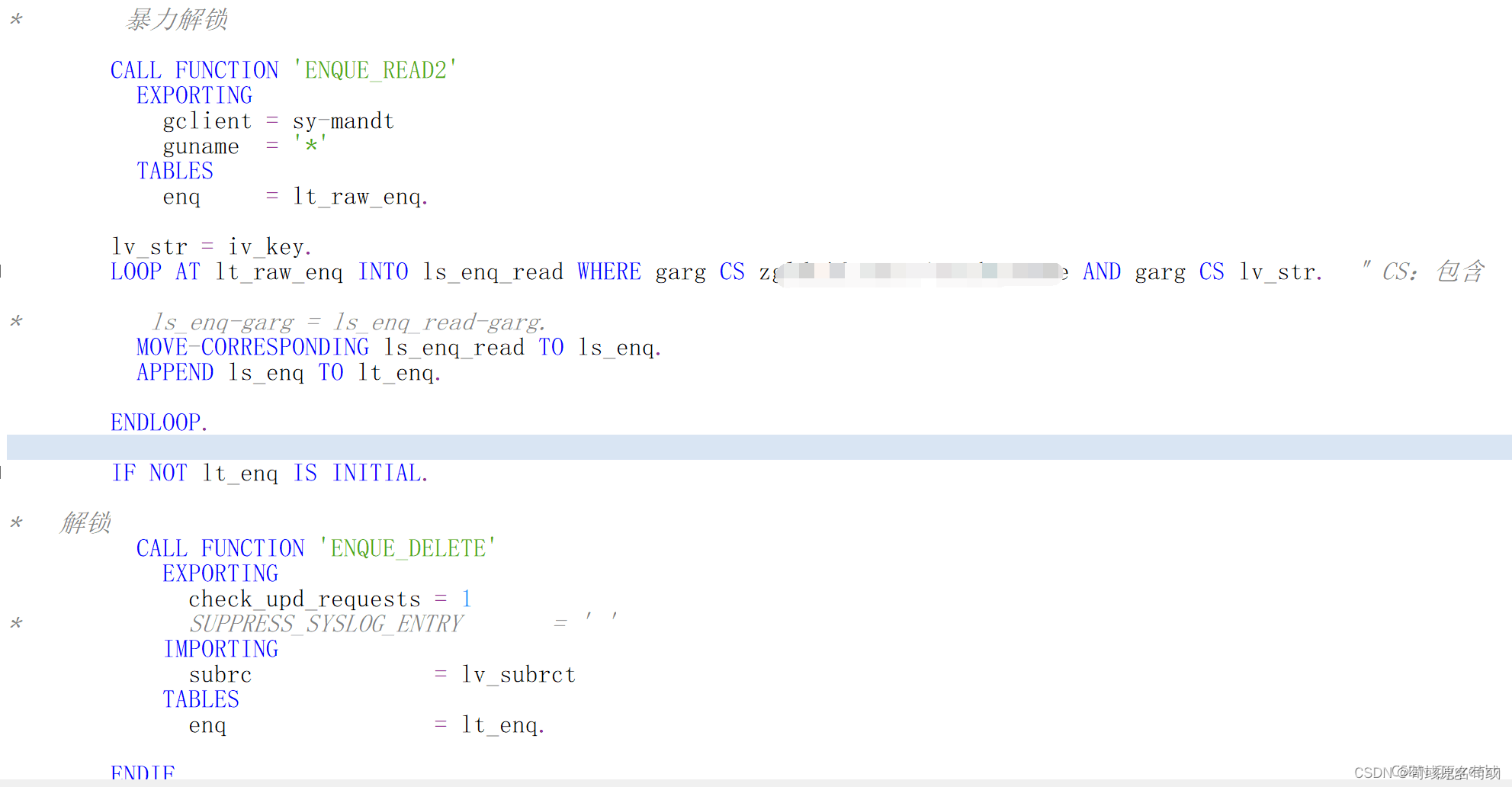
SAP ABAP通过代码解锁SM12中被锁定目标<转载>(RFC: ENQUEUE_READ和 ENQUE_DELETE)
原文链接:https://blog.csdn.net/sinat_38119716/article/details/121406275 备注 RFC:ENQUEUE_READ 读取的是SM12的数据 RFC:ENQUEUE_READ2 读取的是SMENQ的数据 SM12 和 SMENQ 的数据其实是一样的,只是一个是旧的TCODE 一个是新的 解锁用的都是RFC: …...
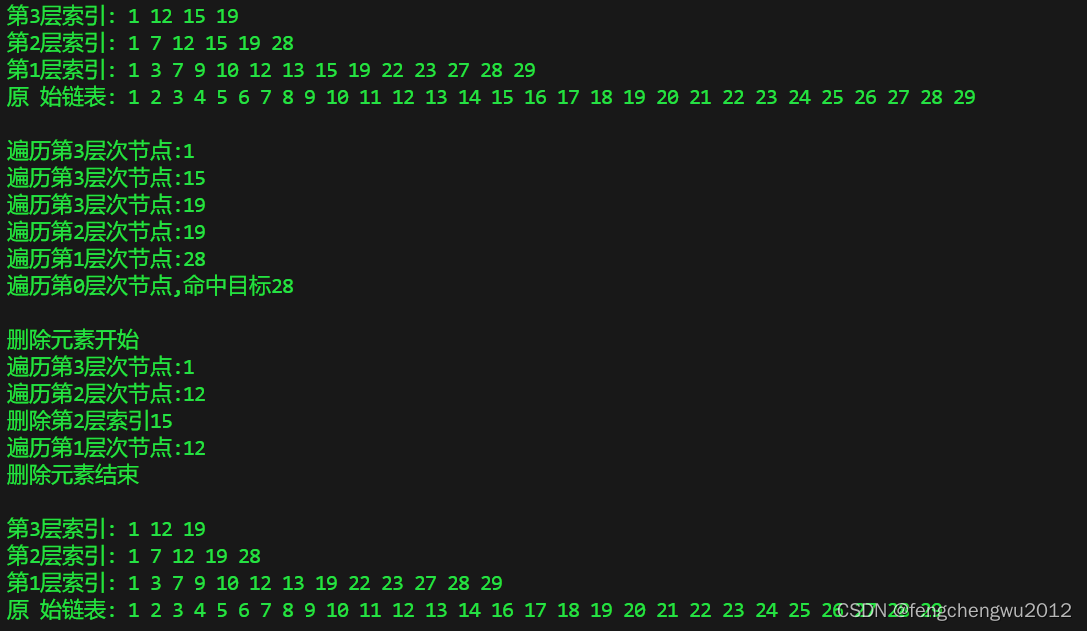
跳跃表原理及实现
一、跳表数据结构 跳表是有序表的一种,其底层是通过链表实现的。链表的特点是插入删除效率高,但是查找节点效率很低,最坏的时间复杂度是O(N),那么跳表就是解决这一痛点而生的。 为了提高查询效率,我们可以给链表加上索…...

详解Vue3中的鼠标事件mousemove、mouseover和mouseout
本文主要介绍Vue3中的常见鼠标事件mousemove、mouseover和mouseout。 目录 一、mousemove——鼠标移动事件二、mouseover——鼠标移入事件三、mouseout——鼠标移出事件 下面是Vue 3中常用的鼠标事件mousemove、mouseover和mouseout的详解。 一、mousemove——鼠标移动事件 鼠…...

Java:socket编程
目录 1、主程序 2、socket任务类 3、jdbc任务类 4、tomcat-jdbc连接池 5、jar包依赖 1、主程序 创建2个线程池,一个用于管理socket连接,一个用来管理jdbc连接。 package socket;import java.io.IOException; import java.net.ServerSocket; import…...
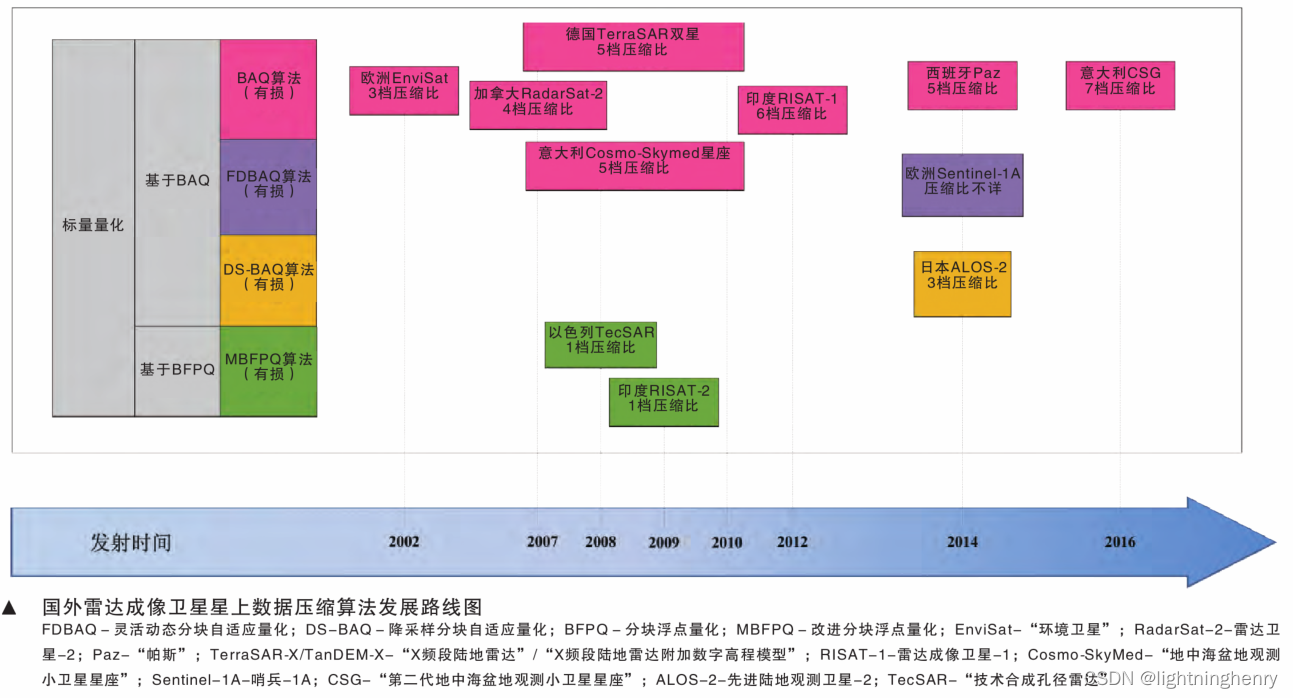
哨兵1号回波数据(L0级)FDBAQ压缩算法详解
本专栏目录: 全球SAR卫星大盘点与回波数据处理专栏目录-CSDN博客 1. 全球SAR卫星回波数据压缩算法统计 各国的SAR卫星的压缩算法按照时间轴排列如下: 可以看出传统的分块BAQ压缩算法(上图粉色)仍然是主流,哨兵1号其实也有传统的BAQ压缩模式。 本文介绍哨兵1号用的FDBAQ算…...

盾构机数据可视化监控平台 | 图扑数字孪生
2002 年,中国 863 计划把盾构机列为国家关键技术,以国家力量为主导,集中力量进行盾构机专项研究。在 2008 年,中国成功研制出属于自己的国产盾构机——中国中铁一号,同时还打通了天津地铁 1500m 的隧道。此举更彻底地打破了国内盾…...
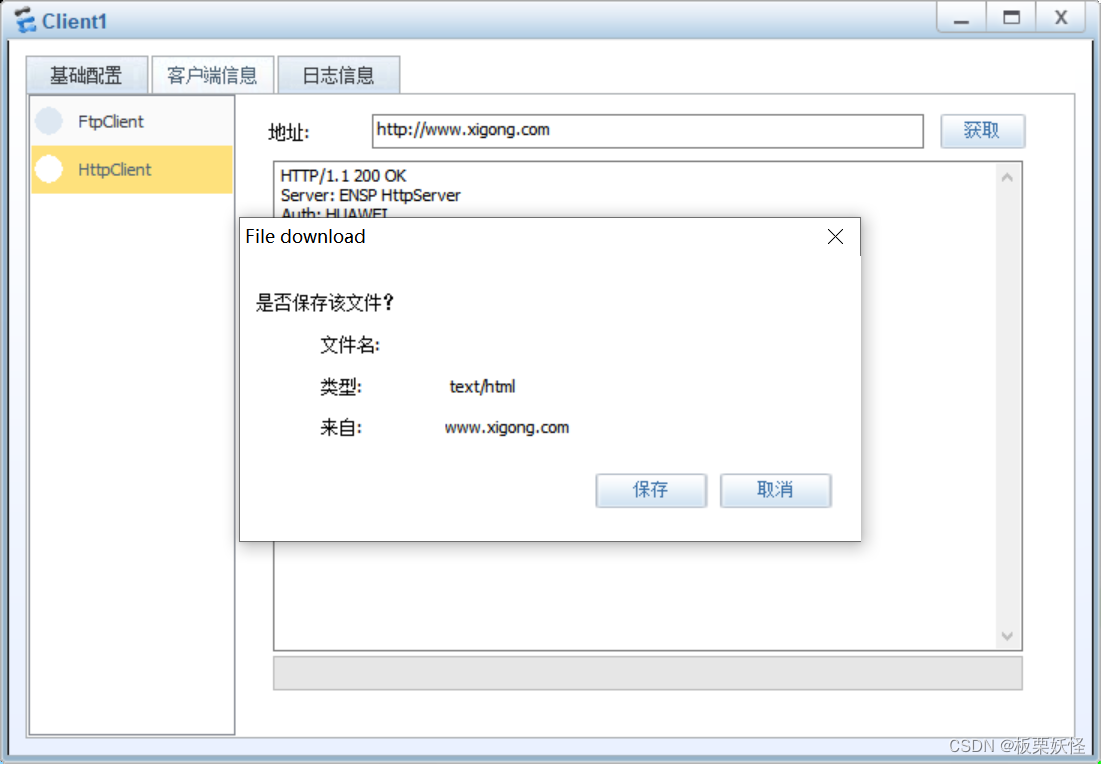
计算机网络课程设计-企业网三层架构
(单人版) 摘 要 本篇报告主要解决了为一家名为西宫的公司网络搭建问题,该网络采用企业网三层架构对完了过进行设计。首先使用以太网中继,主要使用VLAN划分的技术来划定不同部门。使用MSTP对每个组配置生成树,防止交换机…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...

高保真组件库:开关
一:制作关状态 拖入一个矩形作为关闭的底色:44 x 22,填充灰色CCCCCC,圆角23,边框宽度0,文本为”关“,右对齐,边距2,2,6,2,文本颜色白色FFFFFF。 拖拽一个椭圆,尺寸18 x 18,边框为0。3. 全选转为动态面板状态1命名为”关“。 二:制作开状态 复制关状态并命名为”开…...
