奇因子之和(C语言)
题意:
一个整数的因子,就是所有可以整除这个数的数。奇数指在整数中,不能被 2 整除的数。所谓整数 Z 的奇因子,就是可以整除 Z 的奇数。
给定 N 个正整数,请你求出它们的第二大奇因子的和。当然,如果该数只有一个奇因子,就用它唯一的那个奇因子去求和。
输入格式:
输入第一行给出一个正整数 N(≤1000)。随后一行给出 N 个不超过 106 的正整数。
输出格式:
在一行中输出所有给定整数的第二大奇因子之和。
输入样例:
5
147 12 35 78 4
输出样例:
71样例解释:
- 147 的因子有 { 1、3、7、21、49、147 },第二大奇因子是 49;
- 12 的因子有 { 1、2、3、4、6、12 },第二大奇因子是 1;
- 35 的因子有 { 1、5、7、35 },第二大奇因子是 7;
- 78 的因子有 { 1、2、3、6、13、26、39、78 },第二大奇因子是 13;
- 4 的因子有 { 1、2、4 },只有一个奇因子,所以用 1 参与求和。
所以输出的答案是:49+1+7+13+1 = 71。
代码长度限制
16 KB
时间限制
400 ms
内存限制
64 MB
代码如下:
#include <stdio.h>
int test(int a){int cnt=0;while(a%2==0) a/=2;for(int i=1;i*i<=a;i++){if(a%i==0&&(a/i)%2){cnt++;if(2==cnt) return a/i;} } return 1;}
int main(){int a,n,sum=0;scanf("%d",&n);for(int i=0;i<n;i++){scanf("%d",&a);sum+=test(a);}printf("sum==%d",sum);return 0;}相关文章:
)
奇因子之和(C语言)
题意: 一个整数的因子,就是所有可以整除这个数的数。奇数指在整数中,不能被 2 整除的数。所谓整数 Z 的奇因子,就是可以整除 Z 的奇数。 给定 N 个正整数,请你求出它们的第二大奇因子的和。当然,如果该数只…...

简单FTP客户端软件开发——VMware安装Linux虚拟机(命令行版)
VMware安装包和Linux系统镜像: 链接:https://pan.baidu.com/s/1UwF4DT8hNXp_cV0NpSfTww?pwdxnoh 提取码:xnoh 这个学期做计网课程设计【简单FTP客户端软件开发】需要在Linux上配置 ftp服务器,故此用VMware安装了Linux虚拟机&…...
ArkTS开发实践
声明式UI基本概念 应用界面是由一个个页面组成,ArkTS是由ArkUI框架提供,用于以声明式开发范式开发界面的语言。 声明式UI构建页面的过程,其实是组合组件的过程,声明式UI的思想,主要体现在两个方面: 描述…...

vue项目中实现预览pdf
vue项目中实现预览pdf 1. iframe <iframe :src"pdfSrc"></iframe> data() {return {pdfSrc: http://192.168.0.254:19000/trend/2023/12/27/5635529375174c7798b5fabc22cbec45.pdf,}},iframe {width: 100%;height: calc(100vh - 132px - 2 * 20px -…...
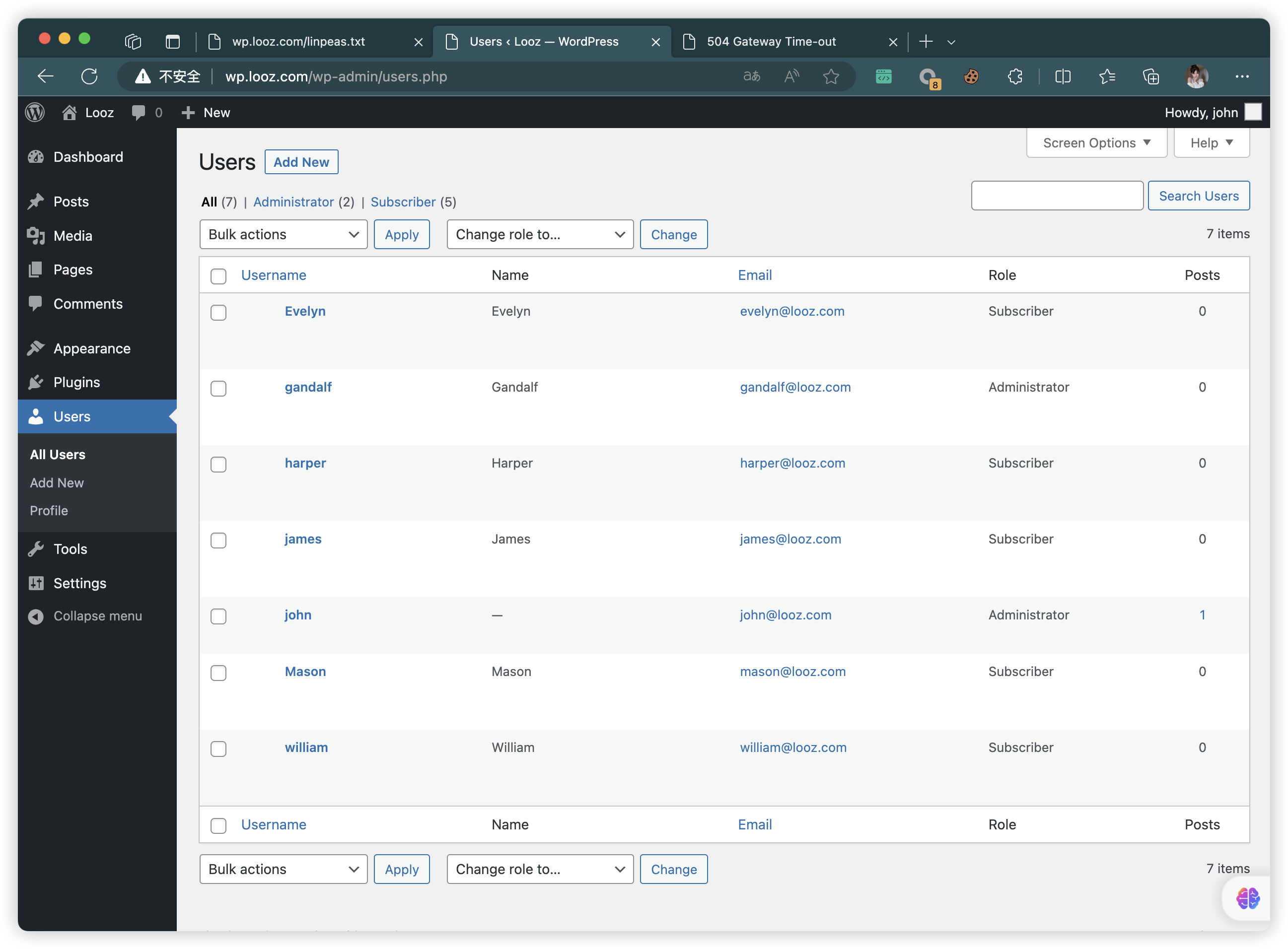
【Vulnhub 靶场】【Looz: 1】【简单】【20210802】
1、环境介绍 靶场介绍:https://www.vulnhub.com/entry/looz-1,732/ 靶场下载:https://download.vulnhub.com/looz/Looz.zip 靶场难度:简单 发布日期:2021年08月02日 文件大小:2.1 GB 靶场作者:mhz_cyber &…...

计算机基础面试题 |03.精选计算机基础面试题
🤍 前端开发工程师(主业)、技术博主(副业)、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云…...

SQL最消耗性能查询错误用法示例
查询性能的消耗主要取决于查询的复杂度、表的大小以及使用的索引等因素。以下是一些查询中常见的错误用法示例,它们可能导致性能问题: 全表扫描: 错误用法示例: SELECT * FROM your_table;这种查询会检索表中的所有行,…...
面向对象编程)
Python学习笔记(六)面向对象编程
最近准备HCIE的考试,用空余时间高强度学习python 介绍了Python中面向对象编程的基本概念,包括类、类的属性、类的方法、类的方法中实例方法、类方法、静态方法,在类与对象中动态添加属性和方法,以及继承、类变量、多态等概念 类…...
CCNP课程实验-05-Comprehensive_Experiment
目录 实验条件网络拓朴 基础配置实现IGP需求:1. 根据拓扑所示,配置OSPF和EIGRP2. 在R3上增加一个网段:33.33.33.0/24 (用Loopback 1模拟) 宣告进EIGRP,并在R3上将EIGRP重分布进OSPF。要求重分布进OSPF后的路由Tag值设置为666&…...

第3课 使用FFmpeg获取并播放音频流
本课对应源文件下载链接: https://download.csdn.net/download/XiBuQiuChong/88680079 FFmpeg作为一套庞大的音视频处理开源工具,其源码有太多值得研究的地方。但对于大多数初学者而言,如何快速利用相关的API写出自己想要的东西才是迫切需要…...

Java 动态树的实现思路分析
Java 动态树的实现 目录概述需求: 设计思路实现思路分析1. 简单Java实现:2.建立父子表存储3.前端的对应的json 字符串方式 参考资料和推荐阅读 Survive by day and develop by night. talk for import biz , show your perfect code,full busy࿰…...
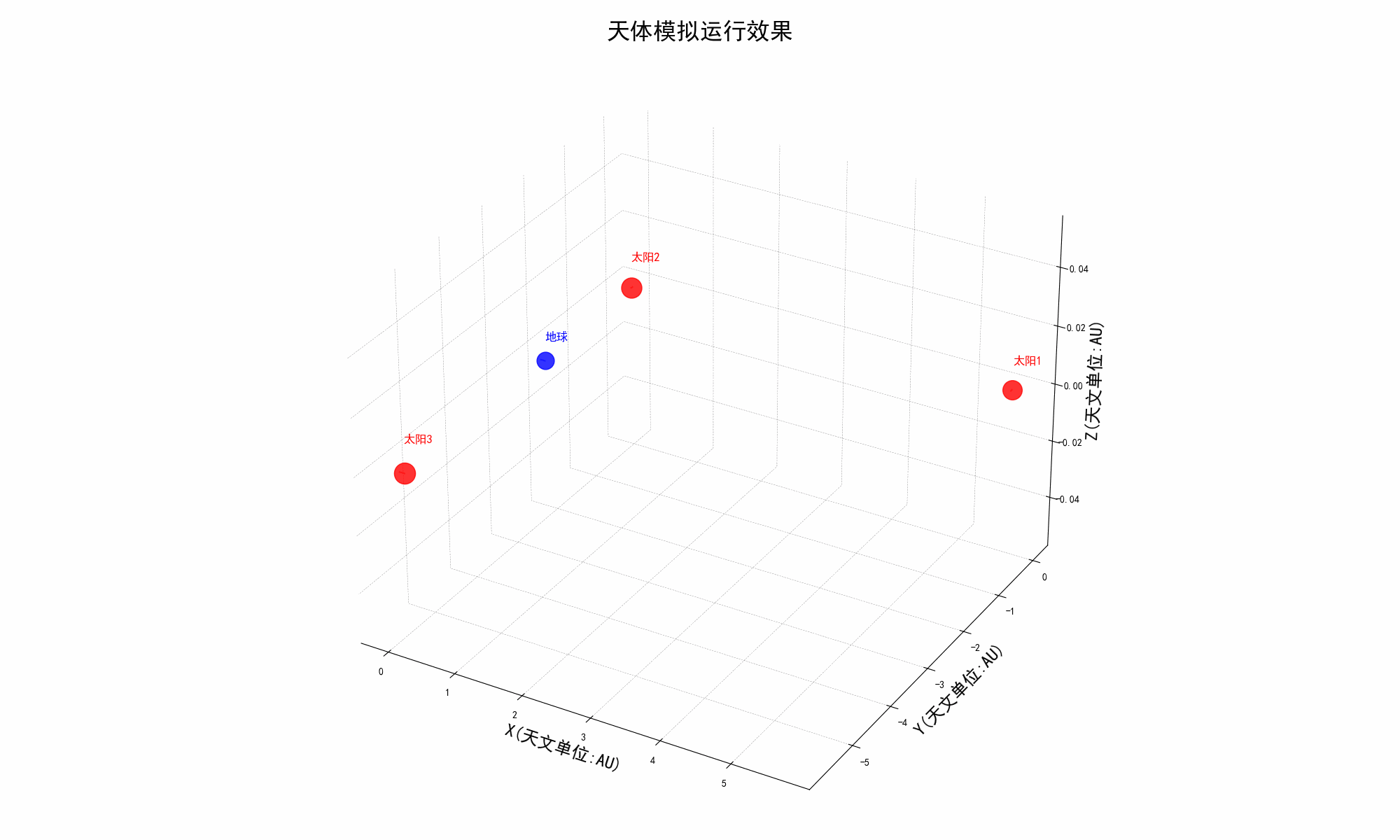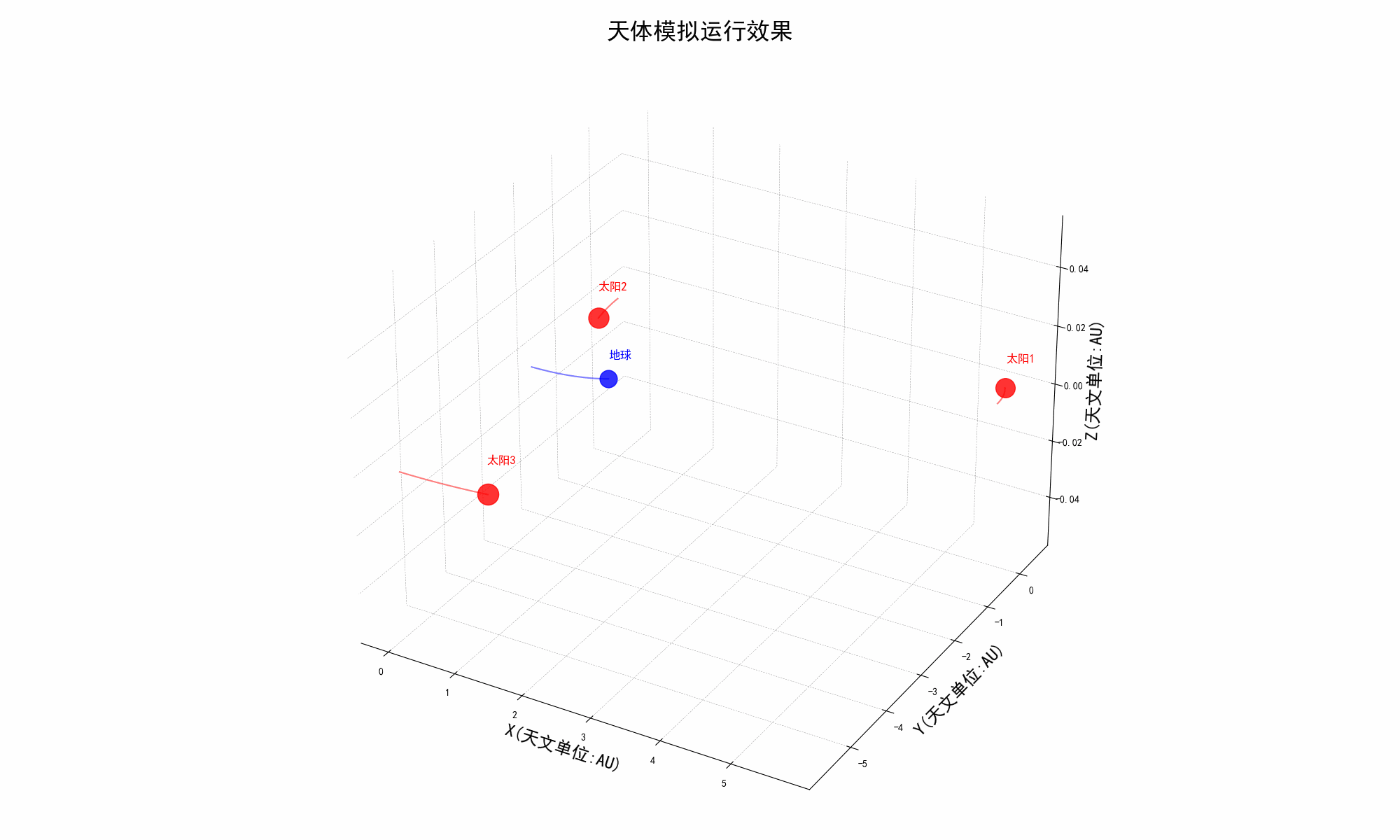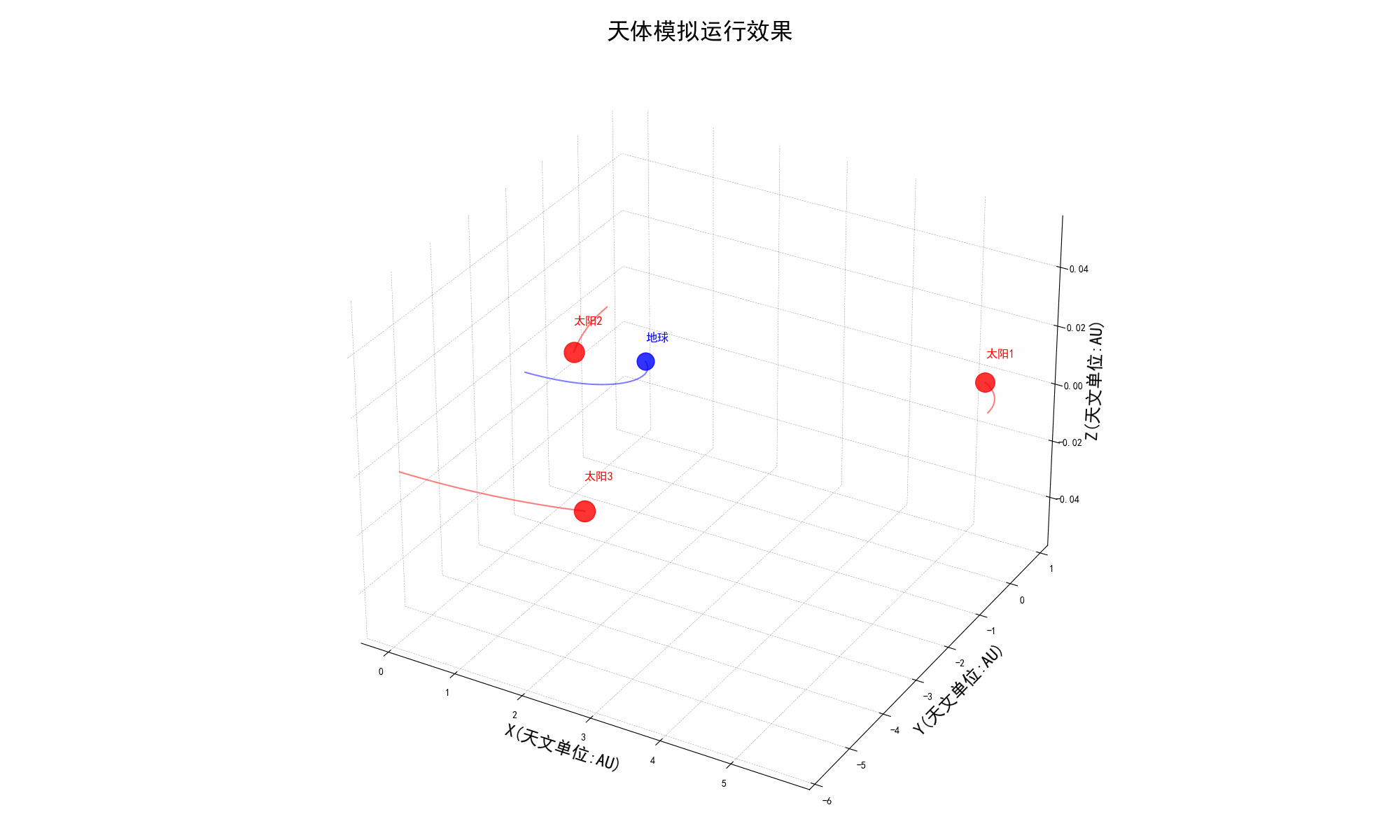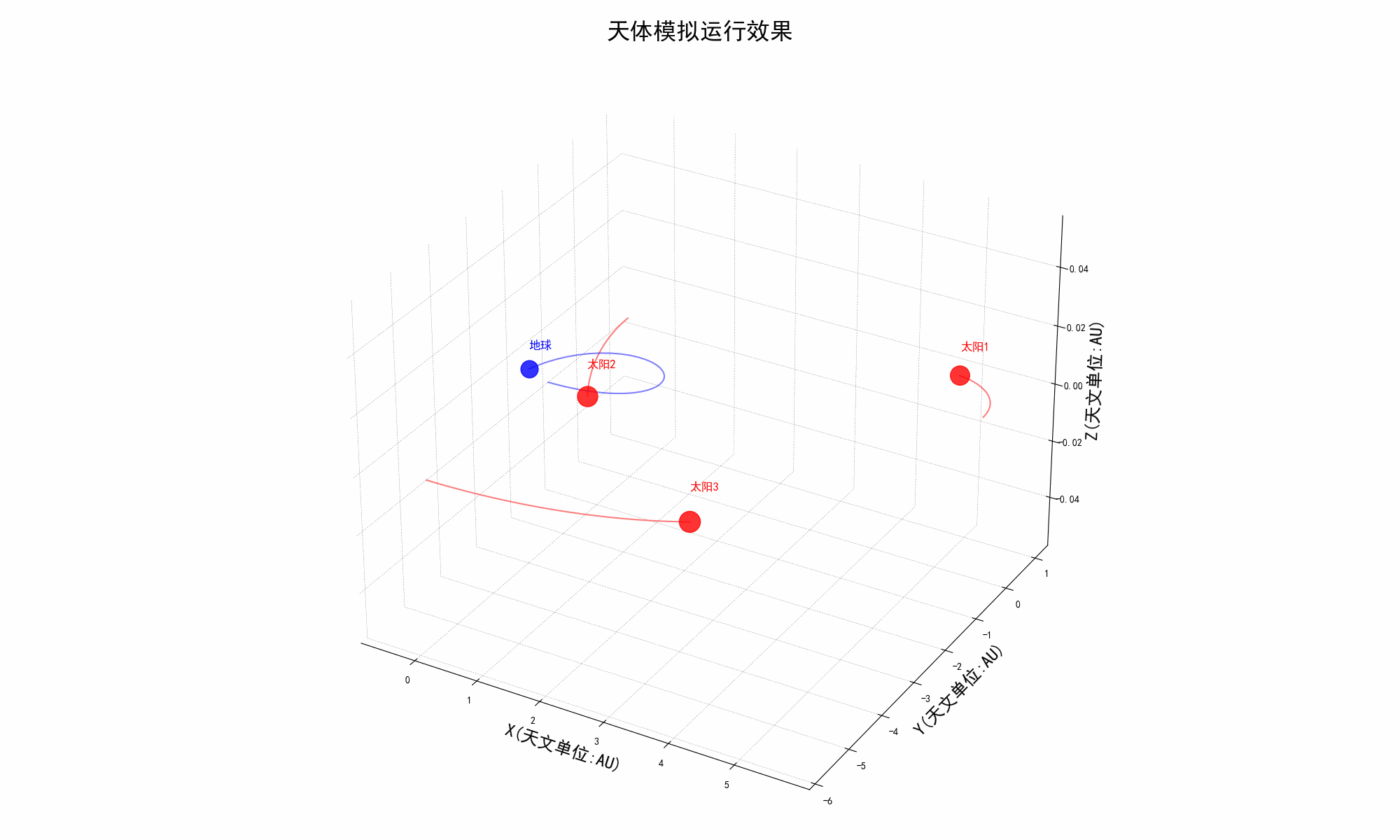
太阳系三体模拟器
介绍 《三体》是刘慈欣创作的长篇科幻小说,文中提到的三体问题比较复杂和无解。 该项目代码就是利用 Python 来模拟三体的运行,此项目代码完全共享,欢迎下载。 我们可以自己通过调整天体的初始坐标、质量和矢量速度等等参数来自定义各种场景…...
SQL常见面试题
今天刷了一遍牛客里的必知必会题,一共50道题,大部分都比较基础,下面汇总一下易错题。 SQL81 顾客登录名 本题几个关键点: 登录名是其名称和所在城市的组合,因此需要使用substring()和concat()截取和拼接字段。得到登…...

怎么获取客户端真实IP?GO
在使用 Golang 的 net/rpc 包进行 RPC 服务开发时,我们有时候会遇到需要获取客户端的真实 IP 和当前连接 net.Conn 的需求。然而在 net/rpc 的服务处理方法中,并没有提供直接获取到这些信息的途径。 那么,我们应该如何去获取这些信息呢&…...

山海鲸可视化软件的优势:数据整合、可视化与个性化定制
随着科技的快速发展,企业数字化转型已成为必然趋势。而对于一些本身没有开发优势或非技术型企业,数字化产品的选择就成为重中之重。作为山海鲸可视化软件的开发者,我们深知这一点,对于企业来说,能选择一个产品一定要有…...

Mybatis行为配置之Ⅰ—缓存
专栏精选 引入Mybatis Mybatis的快速入门 Mybatis的增删改查扩展功能说明 mapper映射的参数和结果 Mybatis复杂类型的结果映射 Mybatis基于注解的结果映射 Mybatis枚举类型处理和类型处理器 再谈动态SQL Mybatis配置入门 Mybatis行为配置之Ⅰ—缓存 Mybatis行为配置…...

【Java开发岗面试】八股文—计算机网络
声明: 背景:本人为24届双非硕校招生,已经完整经历了一次秋招,拿到了三个offer。本专题旨在分享自己的一些Java开发岗面试经验(主要是校招),包括我自己总结的八股文、算法、项目介绍、HR面和面试…...
)
【PythonRS】基于矢量范围批量下载遥感瓦片高清数据(天地图、高德、谷歌等)
这个是之前写的代码了,正好今天有空所以就和大家分享一下。我们在处理项目时,有时候需要高清底图作为辅助数据源去对比数据,所以可能会需要卫星数据。所以今天就和大家分享一下如何使用Python基于矢量范围批量下载高清遥感瓦片数据。 1 读取矢…...
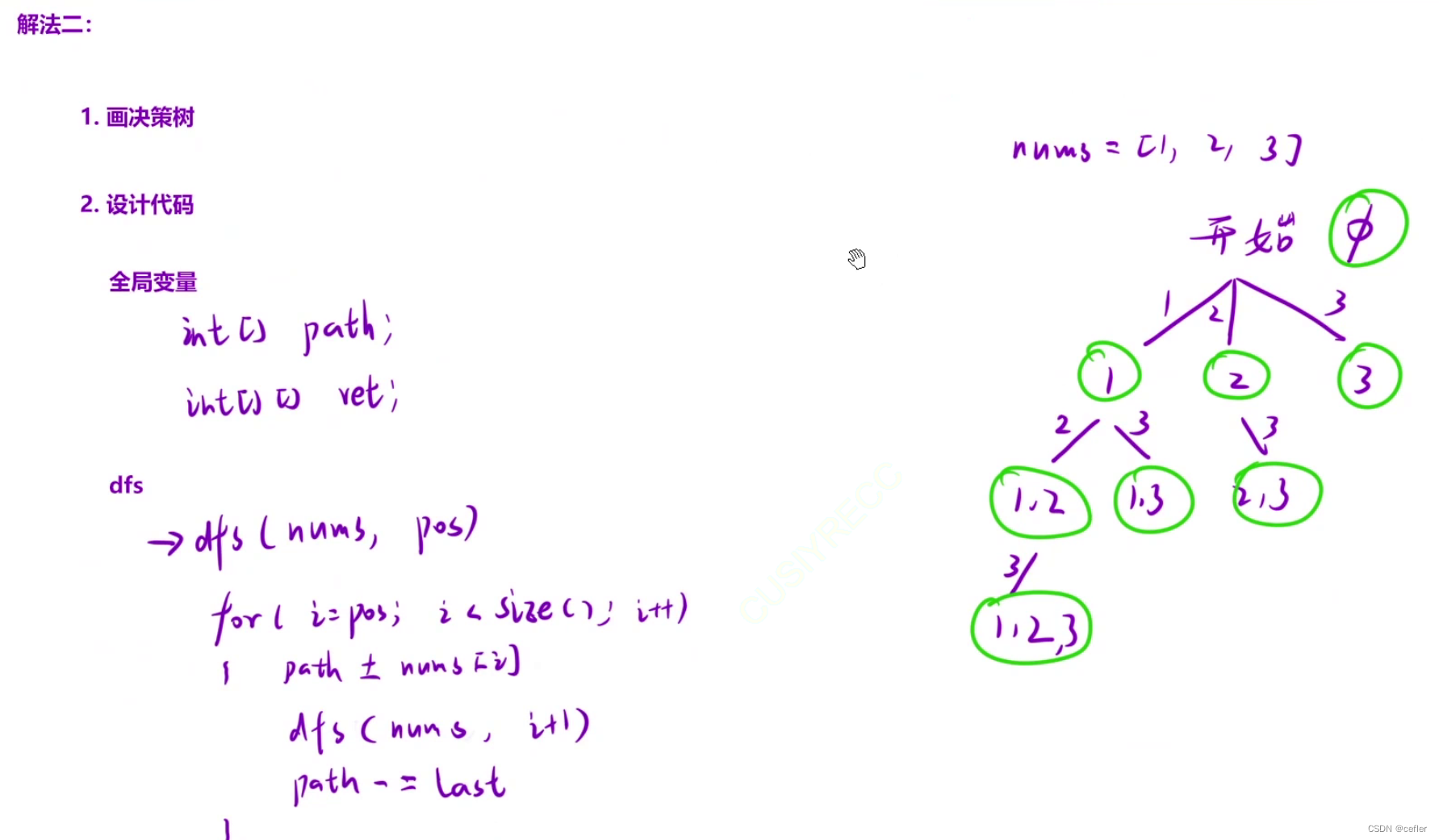
穷举vs暴搜vs深搜vs回溯vs剪枝
欢迎来到Cefler的博客😁 🕌博客主页:那个传说中的man的主页 🏠个人专栏:题目解析 🌎推荐文章:题目大解析(3) 目录 👉🏻全排列👉&#…...
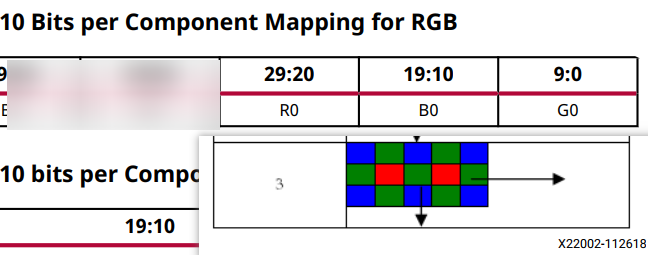
Sensor Demosaic IP 手册PG286笔记
《 UG1449 Multimedia User Guide》中包含了大量的多媒体IP简介。 本IP 用于对bayer RGB(每个pixel只有单个R/G/B)做去马赛克处理,恢复成每个pixel点都有完整的RGB值。通过axi接口配置IP内部erg。 1、算法手册中的描述 提到了几种插值算法&…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

算法250609 高精度
加法 #include<stdio.h> #include<iostream> #include<string.h> #include<math.h> #include<algorithm> using namespace std; char input1[205]; char input2[205]; int main(){while(scanf("%s%s",input1,input2)!EOF){int a[205]…...
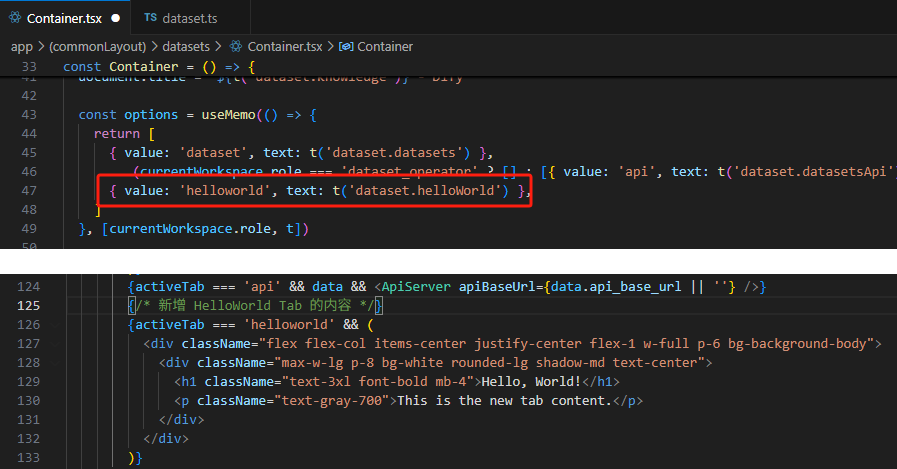
【技巧】dify前端源代码修改第一弹-增加tab页
回到目录 【技巧】dify前端源代码修改第一弹-增加tab页 尝试修改dify的前端源代码,在知识库增加一个tab页"HELLO WORLD",完成后的效果如下 [gif01] 1. 前端代码进入调试模式 参考 【部署】win10的wsl环境下启动dify的web前端服务 启动调试…...

PostgreSQL 与 SQL 基础:为 Fast API 打下数据基础
在构建任何动态、数据驱动的Web API时,一个稳定高效的数据存储方案是不可或缺的。对于使用Python FastAPI的开发者来说,深入理解关系型数据库的工作原理、掌握SQL这门与数据库“对话”的语言,以及学会如何在Python中操作数据库,是…...
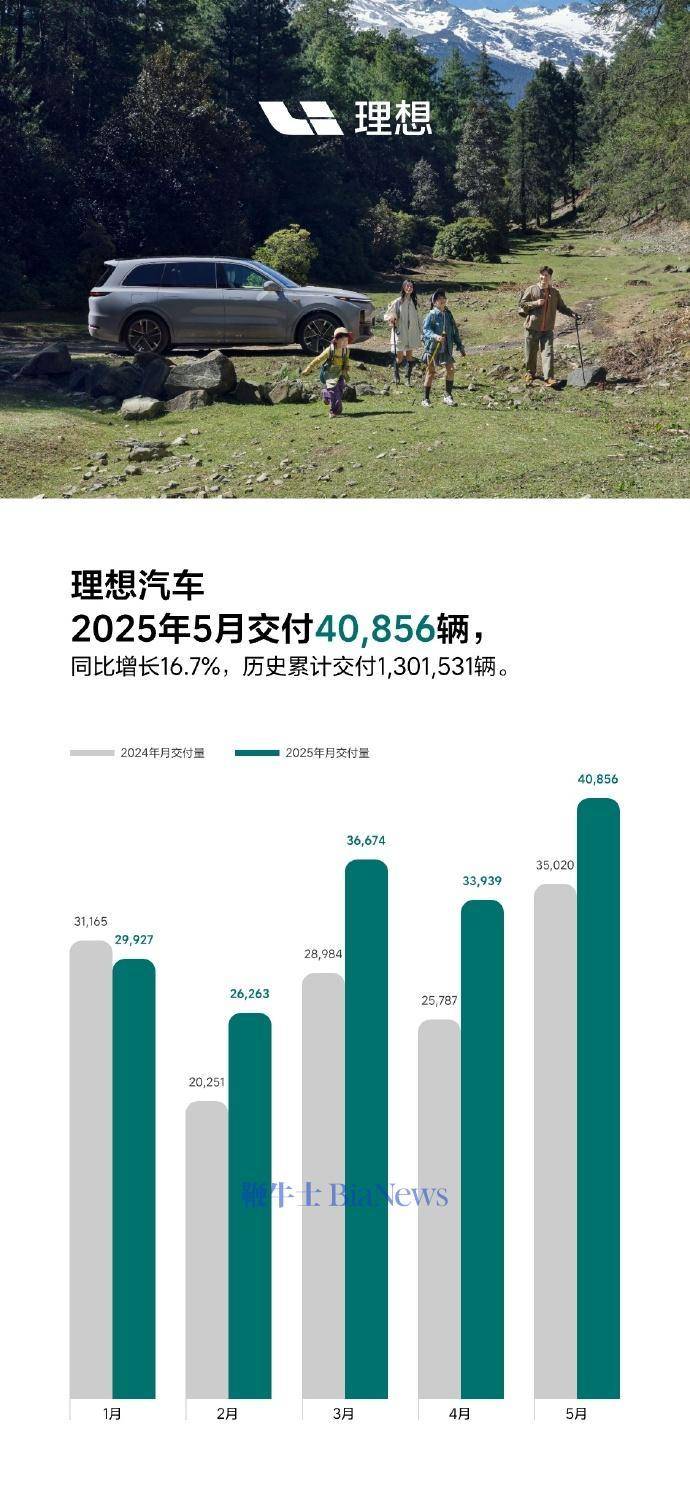
理想汽车5月交付40856辆,同比增长16.7%
6月1日,理想汽车官方宣布,5月交付新车40856辆,同比增长16.7%。截至2025年5月31日,理想汽车历史累计交付量为1301531辆。 官方表示,理想L系列智能焕新版在5月正式发布,全系产品力有显著的提升,每…...
