【教学类-43-14】 20240103 (4宫格数独:正确版:576套) 不重复的基础模板数量:576套
作品展示::——4宫格 576套不重复模板(48页*12套题)

背景需求:
生成4宫格基础模板768套,观看64页内容时,明显看到有错误
【教学类-43-13】 20240103 (4宫格数独:错误版:768套) 不重复的基础模板数量:768套-CSDN博客文章浏览阅读95次,点赞3次,收藏3次。【教学类-43-13】 20240103 (4宫格数独:错误版:768套) 不重复的基础模板数量:768套https://blog.csdn.net/reasonsummer/article/details/135372063

解决思路
最终发现纵向4格不能直接用三个不等于进行通用——第0格数字不等于第4格数字不等于第8格数字不等于第12个数字、
修改成一个对应一个进行不等于,
第0格数字与第4格数字不相等,
第0格数字与第8格数字不相等,
第0格数字与第12格数字不相等,
第4格数字与第8格数字不相等,
第4格数字与第12格数字不相等,
第8格数字与第12格数字不相等,
原理不清楚,反正最后结果数字从786降低到576.应该是排除掉一部分错误的题型。

上代码:
# 测试11*11格,2*2一共4套3*3 宫格
'''
目的:数独14 4宫格有300套不同的基础模板
作者:阿夏
时间:2024年01月03日 13:35'''import random
from win32com.client import constants,gencache
from win32com.client.gencache import EnsureDispatch
from win32com.client import constants # 导入枚举常数模块
import os,timeimport docx
from docx import Document
from docx.shared import Pt
from docx.shared import RGBColor
from docx.enum.text import WD_PARAGRAPH_ALIGNMENT
from docx.oxml.ns import qnfrom docxtpl import DocxTemplate
import pandas as pd
from docx2pdf import convert
from docx.shared import RGBColor# 生成题库
import random
import math
from itertools import permutations# num=int(input('生成几份\n'))
# 制作"单元格"# 几宫格
hsall=4
# int(input('3宫格数独=3\n'))
hs=hsall# kk=int(input('空格数量,输入5,就是50%,就是空一半)\n'))print('------第1步:制作单元格-------')
ll=['3','4','5','6','7','8','9'] # 如果输入345
mm=['43','43','32','32','32','32','32']# 3对应的套数是4*3套
nn=['36','24','36','24','24','24','24']# 3对应的写入单元格的数字大小36磅
for r in range(len(ll)):if hsall ==int(ll[r]):# 底边几套.底边看有2份db=int(mm[r][0])# int(input('底边几套? 3\n'))# 侧边几套 侧边看也是2份print(db ) cb=int(mm[r][1])# int(input('侧边几套? 2\n'))print(cb)size=int(nn[r])print(size) # 写入单元格数字的大小(撑满格子)# 新建一个”装N份word和PDF“的临时文件夹
imagePath1=r'C:\Users\jg2yXRZ\OneDrive\桌面\数独\零时Word'
if not os.path.exists(imagePath1): # 判断存放图片的文件夹是否存在os.makedirs(imagePath1) # 若图片文件夹不存在就创建# 计算不同模板中的单元格坐标,放在bg里
# 棋盘格子数量,# 如果正方形:底边2*侧边2,就是3*3宫格 2*2=4套,底边边格子数量就是3*2+1=7,侧边格子数量就是3*2+1=7,
# 如果长方形:底边3*侧边2,就是3*3宫格,3*2=6套 底边格子数量就是3*3+2=11,侧边格子数量就是3*2+1=7,
# if db==cb:
db_size = hs*db+db-1
cb_size= hs*cb+cb-1
print('{}宫格排列底{}侧{}共{}套,底边格子数{}'.format(hs,db,cb,db*cb,db_size ))
print('{}宫格排列底{}侧{}共{}套,侧边格子数{}'.format(hs,db,cb,db*cb,cb_size ))# 确定每个宫格的左上角坐标 00 04 40 44
bgszm=[]
for a in range(0,cb_size,hs+1): # 0-11每隔4,写一个坐标 侧边yfor b in range(0,db_size,hs+1): # 0-11每隔4,写一个坐标 侧边xbgszm.append('{}{}'.format('%02d'%a,'%02d'%b))
print(bgszm)
# 3宫格排列底3侧2共6套,底边格子数11
# 3宫格排列底3侧2共6套,侧边格子数7
# ['0000', '0004', '0008', '0400', '0404', '0408']# 转为元祖
start_coordinates = [(int(s[0:2]), int(s[2:4])) for s in bgszm]
cell_coordinates = []# 推算每个起始格子后面的单元格数字
for start_coord in start_coordinates:i, j = start_coordsubgrid_coordinates = []for x in range(hs):for y in range(hs):subgrid_coordinates.append((i + x, j + y))cell_coordinates.append(subgrid_coordinates)# 打印结果(元祖样式)
bg=[]
for coordinates in cell_coordinates:# print(coordinates) # [(4, 8), (4, 9), (4, 10), (5, 8), (5, 9), (5, 10), (6, 8), (6, 9), (6, 10)]for c in coordinates:print(c) # 元组 (1, 2) 样式s = ''.join(str(num).zfill(2) for num in c) # zfill将元组 (1, 2) 转换为字符串 '0102' 特别是(5,10)这种必须转成2个数字0510print(str(s)) # '12'bg.append(s) # '0102'
print(bg)print('------第2步:制作3宫格的12套题的内容-------')# 制作3宫格的12套题目(没有空格,只有基础模板)
lst=[]
for b in range(1,hs+1):lst.append(b)
print(lst)permutations_list = list(permutations(lst))
numbers = [list(permutation) for permutation in permutations_list]
# print(numbers)
# [[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]]
# 6种组合# 互相组合成3组
import itertools# 计算排列数量并生成所有可能的排列
combinations2 = list(itertools.permutations(numbers, hs))# 输出排列数量
# print(len(combinations2))
# 120# # 把所有数字都提取成元素
ll=[]
for o1 in combinations2:for o2 in o1:for o3 in o2:ll.append(o3)
# print(ll)
# print(len(ll))
# 1080v=hs*hs
# 16个数字抽取一组
f=[]
for i in range(int(len(ll)/v)):f.append(ll[i*v:i*v+v])
# print(f)
# print(len(f))
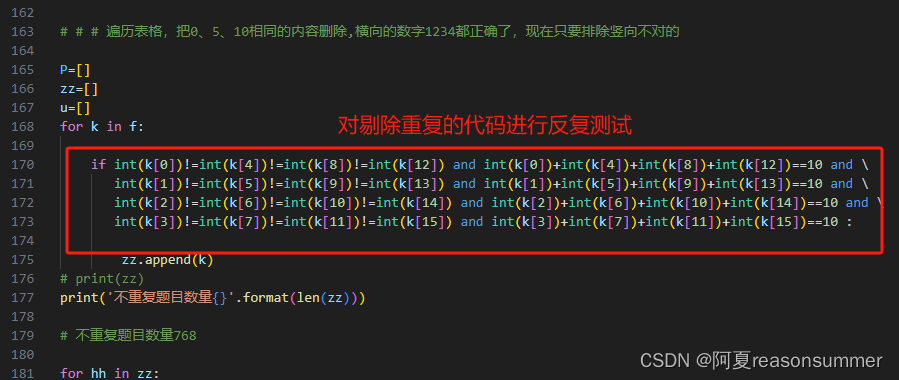
#120条# # # 遍历表格,把0、5、10相同的内容删除,横向的数字1234都正确了,现在只要排除竖向不对的P=[]
zz=[]
u=[]
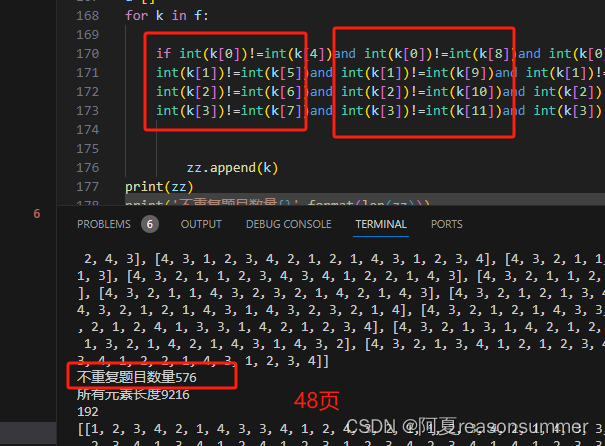
for k in f: if int(k[0])!=int(k[4])and int(k[0])!=int(k[8])and int(k[0])!=int(k[12]) and int(k[4])!=int(k[8]) and int(k[4])!=int(k[12])and int(k[8])!=int(k[12]) and int(k[0])+int(k[4])+int(k[8])+int(k[12])==10 and \int(k[1])!=int(k[5])and int(k[1])!=int(k[9])and int(k[1])!=int(k[13]) and int(k[5])!=int(k[9]) and int(k[5])!=int(k[13])and int(k[9])!=int(k[13]) and int(k[1])+int(k[5])+int(k[9])+int(k[13])==10 and \int(k[2])!=int(k[6])and int(k[2])!=int(k[10])and int(k[2])!=int(k[14]) and int(k[6])!=int(k[10]) and int(k[6])!=int(k[14])and int(k[10])!=int(k[14]) and int(k[2])+int(k[6])+int(k[10])+int(k[14])==10 and\int(k[3])!=int(k[7])and int(k[3])!=int(k[11])and int(k[3])!=int(k[15]) and int(k[7])!=int(k[11]) and int(k[7])!=int(k[15])and int(k[11])!=int(k[15]) and int(k[3])+int(k[7])+int(k[11])+int(k[15])==10:zz.append(k)
print(zz)
print('不重复题目数量{}'.format(len(zz)))# 不重复题目数量768for hh in zz:for ss in hh:u.append(ss)
# print(u)
print('所有元素长度{}'.format(len(u)))
# 所有元素长度12288# 27个16元素,在一页上
bb=hs*hs*db*cb
print(bb)
# 4*4*4*3=192. 64张
for kk in range(int(len(u)/int(bb))): # bb=192,kk=0-64P.append(u[kk*bb:kk*bb+bb])
print(P)
print(len(P))
# 12道题目print('------第3步:写入docx,word表格正好12格子,写入1页12个-------')
# 这里
for z in range(len(P)):doc = Document(r'C:\Users\jg2yXRZ\OneDrive\桌面\数独\数独长方形({}宫格).docx'.format(hs)) # table = doc.tables[0] # 表0,表2 写标题用的# 标题写入3、5单元格 for t in range(0,len(bg)): # 0-5是最下面一行,用来写卡片数字pp=int(bg[t][0:2]) # qq=int(bg[t][2:4])k=str(P[z][t]) # 提取list图案列表里面每个图形 t=索引数字print(pp,qq,k)# 图案符号的字体、大小参数run=table.cell(pp,qq).paragraphs[0].add_run(k) # 在单元格0,0(第1行第1列)输入第0个图图案run.font.name = '黑体'#输入时默认华文彩云字体# run.font.size = Pt(46) #输入字体大小默认30号 换行(一页一份大卡片run.font.size = Pt(size) #是否加粗# run.font.color.rgb = RGBColor(150,150,150) #数字小,颜色深0-255run.font.color.rgb = RGBColor(50,50,50) #数字小,颜色深0-255run.bold=True# paragraph.paragraph_format.line_spacing = Pt(180) #数字段间距r = run._elementr.rPr.rFonts.set(qn('w:eastAsia'), '黑体')#将输入语句中的中文部分字体变为华文行楷table.cell(pp,qq).paragraphs[0].alignment = WD_PARAGRAPH_ALIGNMENT.CENTER#居中 doc.save(r'C:\Users\jg2yXRZ\OneDrive\桌面\数独\零时Word\{}.docx'.format('%02d'%(z+1)))#保存为XX学号的电话号码word time.sleep(2)from docx2pdf import convert# docx 文件另存为PDF文件inputFile = r"C:/Users/jg2yXRZ/OneDrive/桌面/数独/零时Word/{}.docx".format('%02d'%(z+1))# 要转换的文件:已存在outputFile = r"C:/Users/jg2yXRZ/OneDrive/桌面/数独/零时Word/{}.pdf".format('%02d'%(z+1)) # 要生成的文件:不存在# 先创建 不存在的 文件f1 = open(outputFile, 'w')f1.close()# 再转换往PDF中写入内容convert(inputFile, outputFile)print('----------第4步:把都有PDF合并为一个打印用PDF------------')# 多个PDF合并(CSDN博主「红色小小螃蟹」,https://blog.csdn.net/yangcunbiao/article/details/125248205)
import os
from PyPDF2 import PdfMerger
target_path = 'C:/Users/jg2yXRZ/OneDrive/桌面/数独/零时Word'
pdf_lst = [f for f in os.listdir(target_path) if f.endswith('.pdf')]
pdf_lst = [os.path.join(target_path, filename) for filename in pdf_lst]
pdf_lst.sort()
file_merger = PdfMerger()
for pdf in pdf_lst:print(pdf)file_merger.append(pdf)file_merger.write("C:/Users/jg2yXRZ/OneDrive/桌面/数独/(打印合集)05长方形数独宫格14.0 {}宫格基础模板共计{}套({}张).pdf" .format(hs,len(zz),z+1))file_merger.close()
# doc.Close()# # print('----------第5步:删除临时文件夹------------')
import shutil
shutil.rmtree('C:/Users/jg2yXRZ/OneDrive/桌面/数独/零时Word') #递归删除文件夹,即:删除非空文件夹time.sleep(3) # 防止转换时报错,预留生成时间48份生成用多长时间?
22:00第0份→22:05 第19份→22:12
大约12分钟
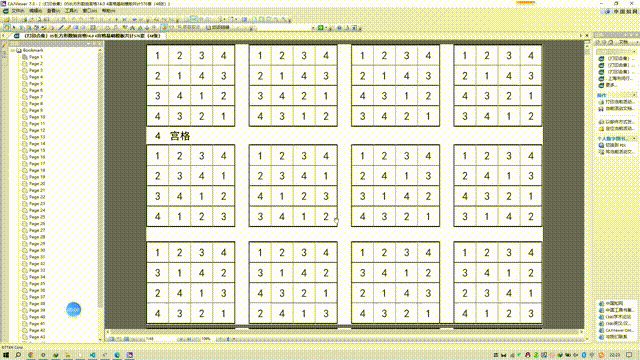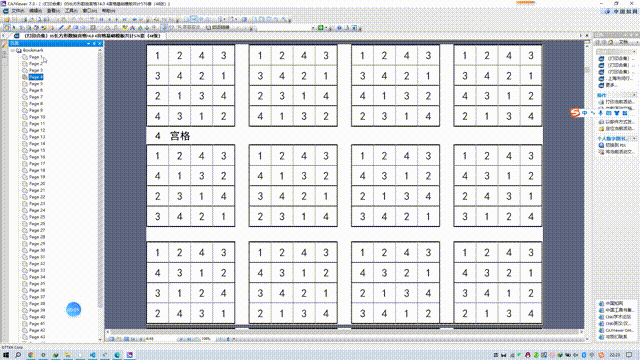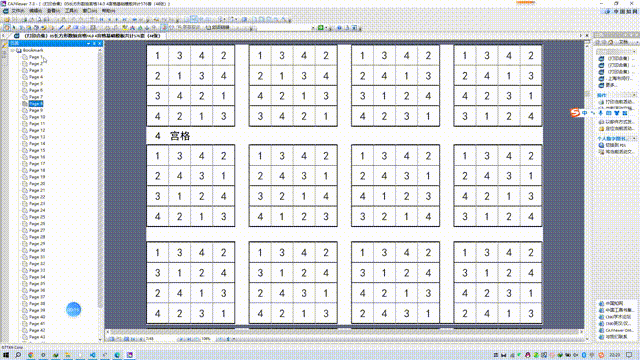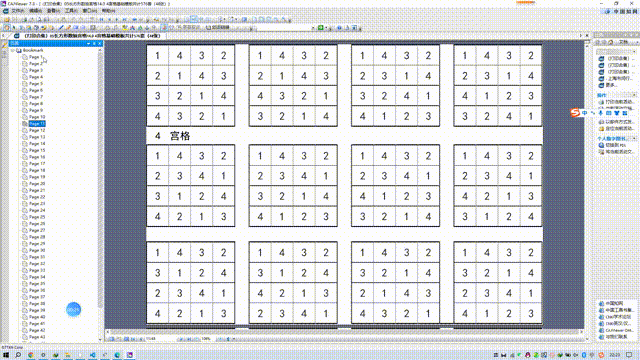
48页12套=576套 目测貌似没有错误(可能有错误,欢迎指出)
后续思考:
1、没想到4宫格16个数字,就有576种数独排列可能,再试试5宫格,希望程序能撑的出那么多数据
2、排除同行、同类相同数字的代码最好能 简化,否则写5宫格的时候会很长很长T_T

相关文章:

【教学类-43-14】 20240103 (4宫格数独:正确版:576套) 不重复的基础模板数量:576套
作品展示::——4宫格 576套不重复模板(48页*12套题) 背景需求: 生成4宫格基础模板768套,观看64页内容时,明显看到有错误 【教学类-43-13】 20240103 (4宫格数独:错误版…...

AIGC开发:调用openai的API接口实现简单机器人
简介 开始进行最简单的使用:通过API调用openai的模型能力 OpenAI的能力如下图: 文本生成模型 OpenAI 的文本生成模型(通常称为生成式预训练 Transformer 或大型语言模型)经过训练可以理解自然语言、代码和图像。这些模型提供文…...
)
c基础(二)
指针: 含义:是一个值,一个值代表着一个内存地址,类似于存放路径 * 运算符 : 1 字符*表示指针 作用:通常跟在类型关键字的后面,表示指针指向的是什么类型的值 int * foo, * bar;声明指针后会…...

人工智能趋势报告解读:ai野蛮式生长的背后是机遇还是危机?
近期,Enterprise WordPress发布了生成式人工智能在营销中的应用程度的报告,这是一个人工智能迅猛发展的时代,目前人工智能已经广泛运用到内容创作等领域,可以预见的是人工智能及其扩展应用还将延伸到我们工作与生活中的方方面面。…...
 (完))
三、C语言中的分支与循环—goto语句 (10) (完)
在C语言中,goto语句允许程序无条件地跳转到同一函数内的标记位置。这个标记位置通过一个标签和冒号(:)来标示。goto语句可以用于从深层嵌套的循环或条件语句中直接跳出,或者跳过某些代码执行。尽管goto语句在某些情况下可以使程序逻辑变得清晰࿰…...

RabbitMQ 常见问题
1. 如何保证消息顺序消费 在RabbitMQ中,消息最终会保存在队列中,在同一个队列中,消息是顺序的,保持先进先出的原则,这个由Rabbitmq保证。而不同队列中的消息,RabbitMQ 是无法保证其顺序性。顺序消费主要是…...

阶段二-Day10-日期类
日期类结构: 1.java.util.Date是日期类 2.DateFormat是日期格式类、SimpleDateFormat是日期格式类的子类 Timezone代表时区 3.Calendar是日历类,GregorianCalendar是日历的子类 一. 常用类-Date 1.1 Date构造方法 Date(long date) 使用给定的毫秒时间价值构建…...
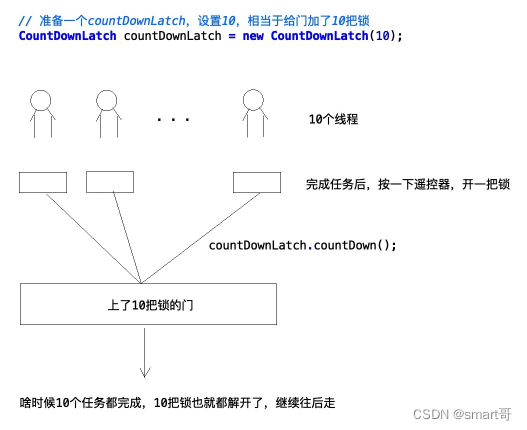
多任务并行处理相关面试题
我自己面试时被问过两次多任务并行相关的问题: 假设现在有10个任务,要求同时处理,并且必须所有任务全部完成才返回结果 这个面试题的难点是: 既然要同时处理,那么肯定要用多线程。怎么设计多线程同时处理任务呢&…...
Shell脚本学习笔记
1. 写在前面 工作中,需要用到写一些shell脚本去完成一些简单的重复性工作, 于是就想系统的学习下shell脚本的相关知识, 本篇文章是学习shell脚本整理的学习笔记,内容参考主要来自C语言中文网, 学习过程中,…...

ROS-安装xacro
安装 运行下列命令进行安装,xxxxxx处更改为自己的版本 sudo apt-get install ros-xxxxxx-xacro运行 输入下列命令 roscd xacro如果没有报错,并且进入了xacro软件包的目录,则表示安装成功。 参考: [1]https://wenku.csdn.net/ans…...

为什么说 $mash 是 Solana 上最正统的铭文通证?
早在 2023 年的 11 月,包括 Solana、Avalanche、Polygon、Arbitrum、zkSync 等生态正在承接比特币铭文生态外溢的价值。当然,因铭文赛道过于火爆,当 Avalanche、BNB Chain 以及 Polygon 等链上 Gas 飙升至极值,Arbitrum、zkSync 等…...
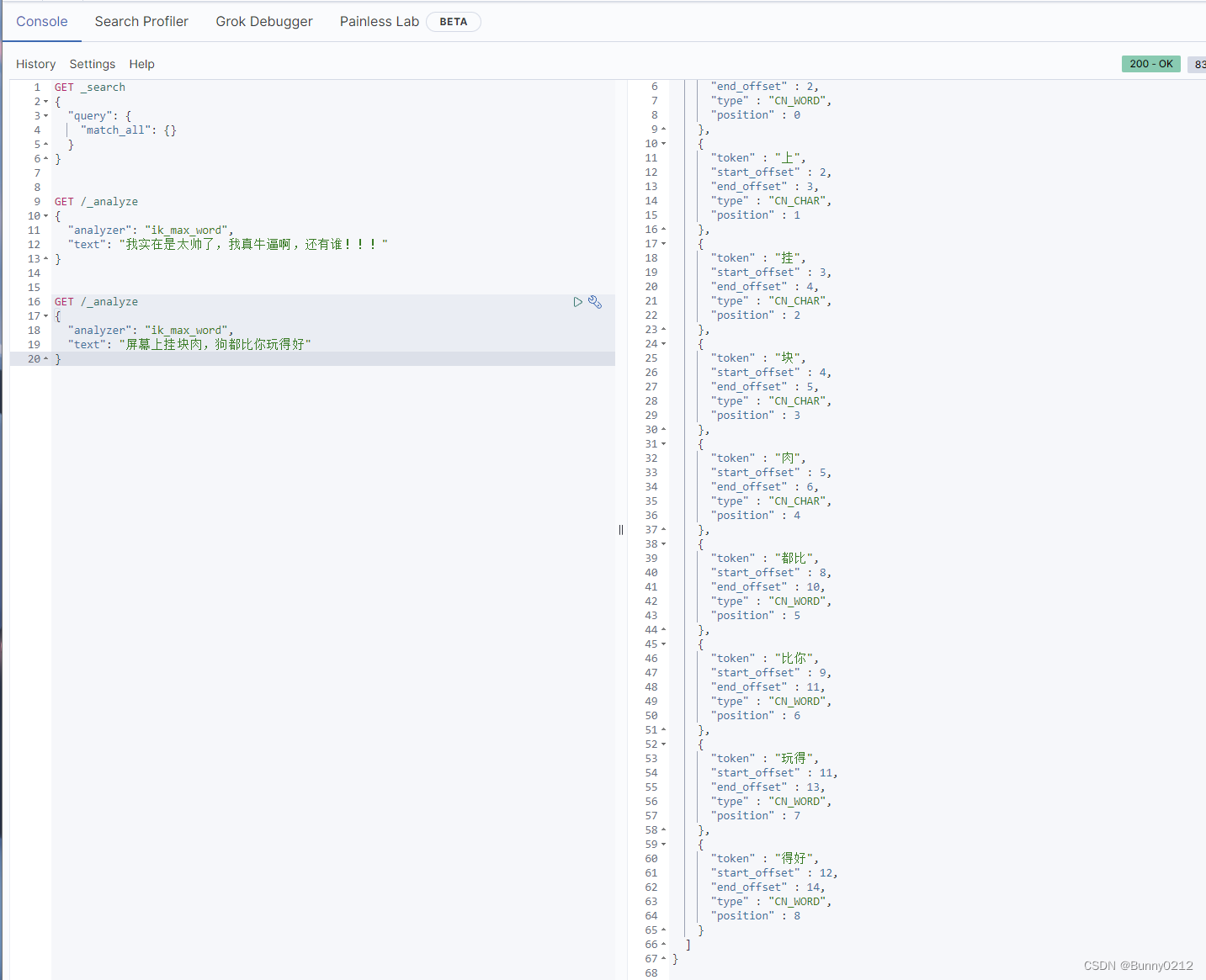
安装elasticsearch、kibana、IK分词器、扩展IK词典
安装elasticsearch、kibana、IK分词器、扩展IK词典 后面还会安装kibana,这个会提供可视化界面方面学习。 需要注意的是elasticsearch和kibana版本一定要一样!!! 否则就像这样 elasticsearch 1、创建网络 因为我们还需要部署k…...

Spring中常见的BeanFactory后处理器
常见的BeanFacatory后处理器 先给出没有添加任何BeanFactory后处理器的测试代码 public class TestBeanFactoryPostProcessor {public static void main(String[] args) {GenericApplicationContext context new GenericApplicationContext();context.registerBean("co…...
)
FPGA LCD1602驱动代码 (已验证)
一.需求解读 1.需求 在液晶屏第一行显示“HELLO FPGA 1234!” 2. 知识背景 1602 液晶也叫 1602 字符型液晶,它是一种专门用来显示字母、数字、符号等的点阵 型液晶模块。它由若干个 5X7 或者 5X11 等点阵字符位组成,每个点阵字符位都可以显示一 个字符,每位之间有一个点距的…...
c++编程要养成的好习惯
1、缩进 你说有缩进看的清楚还是没缩进看的清楚 2、i和i i运行起来和i更快 3、 n%20和n&1 不要再用n%20来判断n是不是偶数了,又慢又土,用n&10,如果n&10就说明n是偶数 同理,n&11说明n是奇数 4、*2和<<…...

后台管理项目的多数据源方案
引言 在互联网开发公司中,往往伴随着业务的快速迭代,程序员可能没有过多的时间去思考技术扩展的相关问题,长久下来导致技术过于单一。为此最近在学习互联网思维,从相对简单的功能开始做总结,比如非常常见的基础数据的…...

视频美颜SDK趋势畅想:未来发展方向与应用场景
当下,视频美颜SDK正不断演进,本文将深入探讨视频美颜SDK的发展趋势,探讨未来可能的方向和广泛的应用场景。 1.深度学习与视频美颜的融合 未来,我们可以期待看到更多基于深度学习算法的视频美颜SDK,为用户提供更高质量…...

C++ const 限定符的全面介绍
C const 限定符的全面介绍 1. const 修饰基本数据类型 定义 const 修饰的基本数据类型变量,值不可改变。 语法 const type variable value;特点 不可变性,增加代码可读性。 作用 定义不可修改的常量。 使用场景 全局常量、配置项。 注意事项…...

Vue 中的 ref 与 reactive:让你的应用更具响应性(上)
🤍 前端开发工程师(主业)、技术博主(副业)、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云…...
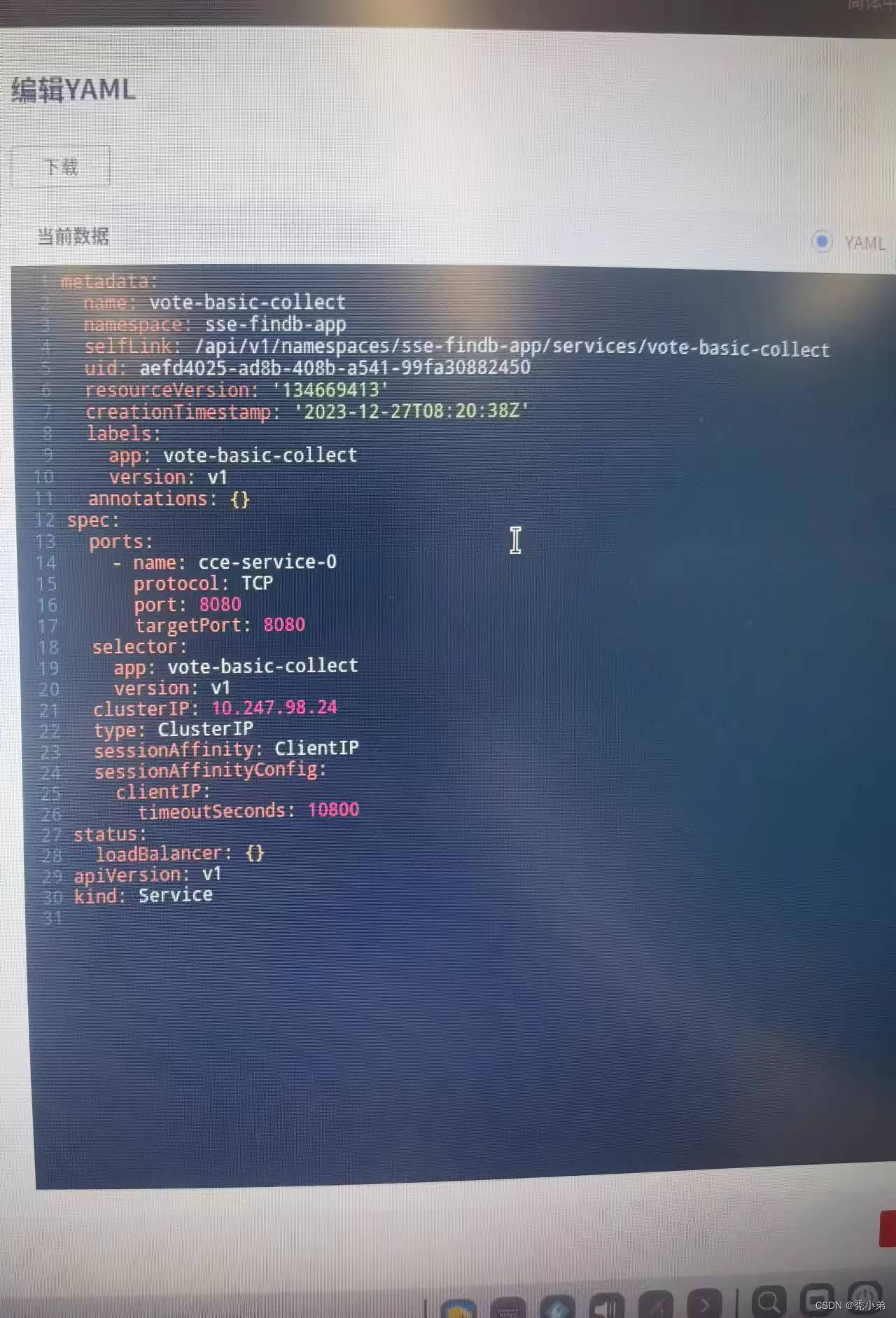
华为云CCE-集群内访问-根据ip访问同个pod
华为云CCE-集群内访问-根据ip访问同个pod 问题描述:架构如下:解决方法: 问题描述: 使用service集群内访问时,由于启用了两个pod,导致请求轮询在两个pod之间,无法返回正确的结果。 架构如下&am…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...
