Acwing---843. n-皇后问题
n-皇后问题
- 1.题目
- 2.基本思想
- 3.代码实现
1.题目
n−皇后问题是指将 n 个皇后放在 n×n 的国际象棋棋盘上,使得皇后不能相互攻击到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。
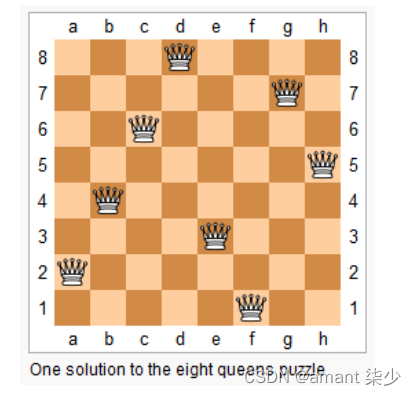
现在给定整数 n,请你输出所有的满足条件的棋子摆法。
输入格式
共一行,包含整数 n。
输出格式
每个解决方案占 n 行,每行输出一个长度为 n 的字符串,用来表示完整的棋盘状态。
其中 . 表示某一个位置的方格状态为空,Q 表示某一个位置的方格上摆着皇后。
每个方案输出完成后,输出一个空行。
注意:行末不能有多余空格。
输出方案的顺序任意,只要不重复且没有遗漏即可。
数据范围
1≤n≤91≤n≤91≤n≤9
输入样例:
4
输出样例:
.Q…
…Q
Q…
…Q.
…Q.
Q…
…Q
.Q…
2.基本思想
DFS 时间复杂度O(n!)
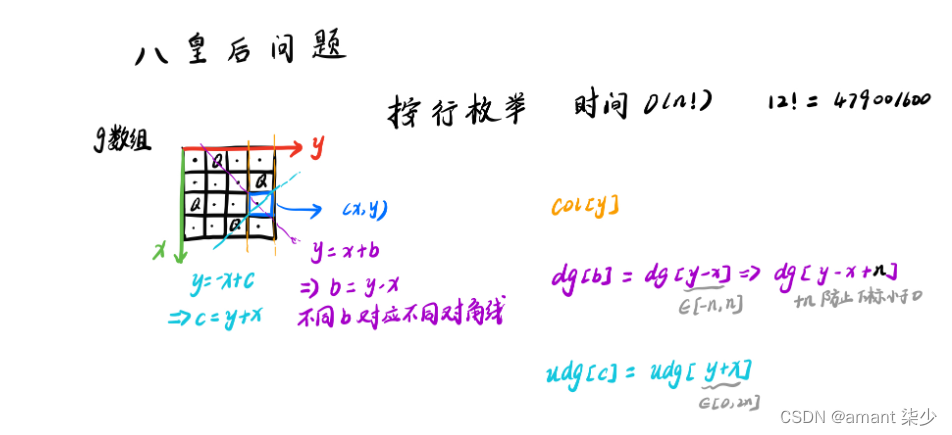
正对角线,y=-x+c,c=x+y,c这里代表截距,反对角线y=x+c,c=y-x,所以这里的c可能是负的,但作为数组下标,不能是负的,所以我们把反对角线加上一个偏移量,c=y-x+n是没影响的,因为截距最大是n,也可以加比n大的任何数
用截距表示对角线,截距相同就说明是同一条对角线
核心目的:找一些合法的下标来表示dg或udg是否被标记过,所以如果你愿意,你取 udg[n+n−u+i]
也可以,只要所有(u,i)对可以映射过去就行.
3.代码实现
import java.util.Scanner;public class _843n皇后问题 {static Scanner sc = new Scanner(System.in);static int N = 20;//增加 了一个 偏移量 n 需要 开 20static int n;static char path[][] = new char[N][N];//保存 路径信息static boolean[] col = new boolean[N];// bool数组用来判断搜索的下一个位置是否可行 col列,dg对角线,udg反对角线static boolean[] dg = new boolean[N];static boolean[] udg = new boolean[N];public static void main(String[] args) {n = sc.nextInt();for (int i = 0; i < n; i++)for (int j = 0; j < n; j++)path[i][j] = '.';dfs(0);}private static void dfs(int u) {if (u == n) {//表示 已经搜素了n行 输出这条路径 信息for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++)System.out.print(path[i][j]);System.out.println();//换行}System.out.println();return;}//对n个位置按行搜索for (int i = 0; i < n; i++) {if (!col[i] && !dg[i + u] && !udg[n + i - u]) {path[u][i] = 'Q';col[i] = dg[u + i] = udg[n + i - u] = true;dfs(u + 1);//枚举 下一行//恢复 回溯col[i] = dg[u + i] = udg[n + i - u] = false;path[u][i] = '.';}}}
}
相关文章:

Acwing---843. n-皇后问题
n-皇后问题1.题目2.基本思想3.代码实现1.题目 n−皇后问题是指将 n 个皇后放在 nn 的国际象棋棋盘上,使得皇后不能相互攻击到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。 现在给定整数 n,请你输出所有的满足条件的棋子摆法。 …...

彻底搞清楚内存泄漏的原因,如何避免内存泄漏,如何定位内存泄漏
作为C/C开发人员,内存泄漏是最容易遇到的问题之一,这是由C/C语言的特性引起的。C/C语言与其他语言不同,需要开发者去申请和释放内存,即需要开发者去管理内存,如果内存使用不当,就容易造成段错误(segment fa…...
自动驾驶目标检测项目实战——基于深度学习框架yolov的交通标志检测
自动驾驶目标检测项目实战——基于深度学习框架yolov的交通标志检测 目前目标检测算法有很多,流行的就有faster-rnn和yolov,本文使用了几年前的yolov3框架进行训练,效果还是很好,当然也可以使用更高版本的Yolov进行实战。本代码使…...

flink兼容性验证
flink介绍:https://blog.csdn.net/weixin_43563705/article/details/107604693 一、安装启动 安装flink及其依赖 yum install java-1.8.0-openjdk curl tar mkdir -p /usr/local/flink wget https://mirrors.aliyun.com/apache/flink/flink-1.16.1/flink-1.16.1-bi…...

智慧工厂数字孪生可视化监测系统有效提升厂区安全管控效力
我国制造业正处于产业升级的关键时期,基于数据进行生产策略制定与管理是大势所趋,而数据可视化以更直观的方式成为数据分析传递信息的重要工具。 深圳华锐视点通过三维可视化手段对工厂各类设备进行三维建模,真实复现设备设施外观、结构、运转…...

c++中基本类型详细解释外加基本运算规则
👀👀#c中包括算数类型和空类型。 类型含义wchat_t宽字符bool布尔类型char字符chat16_tunicode字符chat_32unicode字符short短整型int整形long长整型longlong长整型float单精度浮点型double双精度浮点型longdouble扩展精度浮点型 👀…...

扬帆优配“机器人+”方案加码产业发展,这些股有望高增长
“机器人”发明新需求,2022年中国机器人市场规模约为174亿美元。 美国时刻3月1日,特斯拉在得克萨斯州超级工厂举办投资者日活动,展示了人形机器人Optimus的视频,更夸大的是,视频中的机器人好像在制作另一个机器人&…...
推送投票制作微信推送里投票制作教程在线投票活动制作
近些年来,第三方的微信投票制作平台如雨后春笋般络绎不绝。随着手机的互联网的发展及微信开放平台各项基于手机能力的开放,更多人选择微信投票小程序平台,因为它有非常大的优势。1.它比起微信公众号自带的投票系统、传统的H5投票系统有可以图…...
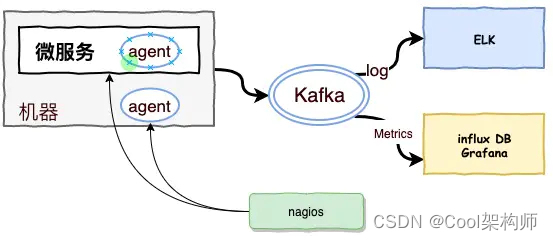
【架构师】跟我一起学架构——微服务分层监控
博客昵称:架构师Cool 最喜欢的座右铭:一以贯之的努力,不得懈怠的人生。 作者简介:一名Coder,软件设计师/鸿蒙高级工程师认证,在备战高级架构师/系统分析师,欢迎关注小弟! 博主小留言…...
Linux:https静态网站搭建案例
目录介绍httpshttps通信过程例介绍https 整个实验是在http实验基础上进行的 因为http协议在传输的时候采用的是明文传输,有安全隐患,所以出现了https(安全套接字层超文本传输协议) HTTPS并不是一个新协议, 而是HTTP…...

前端css整理
如何水平垂直居中一个盒子? 1.已知高度:子盒子设置 display: inline-block; 父盒子设置 line-height 等于高度实现垂直居中;使用 text-align:center实现水平居中 2.父盒子 display:flex; align-items:center;justify-content:center; 3.定位&…...

混凝土搅拌站远程监控解决方案
一、项目背景 随着大规模的基础设施建设,对混凝土搅拌设备的需求量日益增加,对其技术指标的要求也日益提高,其技术性能将直接关系到工程的质量和使用寿命。而混凝土生产的质量是在生产过程中形成的,而非最终强度的检测。混凝土生…...

Spark SQL 学习总结
文章目录(一)Spark SQL(二)SParkSession(三)DataFrame常见算子操作(四)DataFrame的sql操作(五)RDD转换为DataFrame(1)反射方式&#x…...

深度学习 - 37.TF x Keras Deep Cross Network DCN 实现
目录 一.引言 二.模型简介 1.Embedding and stacking layer 2.Cross Network 2.1 模型架构分析 2.2 计算逻辑...
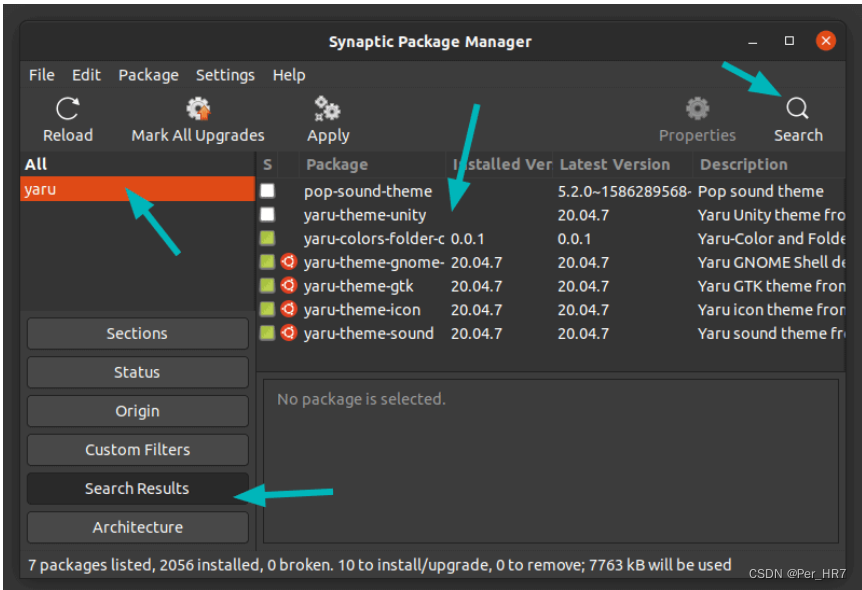
Ubuntu中使用Synaptic进行包管理
Synaptic概况 Synaptic 是一个轻量级的 apt 软件包管理器系统的 GUI 前端,所有你可以在终端中使用 apt-get 命令来做的事,都可以通过 Synaptic 来实现。优势 图形化安装界面,同时可以安装配置相关依赖,避免由于依赖问题导致的各类…...

python之selenium库安装及用法(定位法、获取文本、文本框输入、鼠标点击、滑动滚动条)
一、selenium库安装 pip install selenium二、浏览器驱动安装 谷歌浏览器驱动下载地址:https://chromedriver.storage.googleapis.com/index.html 根据你电脑的谷歌浏览器版本,下载相应的就行。我下载的是110.0.5481.XX中的chromedriver_win32.zip 下载…...

FPGA纯verilog实现图像视频旋转 串口指令控制旋转角度 提供工程源码和技术支持
目录1、前言2、理论基础3、设计思路和框架图像输入和采集图像旋转处理图像缓存图像输出4、vivado工程详解5、上板调试验证6、福利:工程代码的获取1、前言 图像旋转是一种常用的图像处理技术,其基本原理就是指图像以某一点为中心旋转一定的角度ÿ…...

EventGraph:Event Extraction as Semantic Graph Parsing 论文解读
EventGraph: Event Extraction as Semantic Graph Parsing 论文:2022.case-1.2.pdf (aclanthology.org) 代码:huiling-y/EventGraph (github.com) 期刊/会议:CASE 2022 摘要 事件抽取涉及到事件触发词和相应事件论元的检测和抽取。现有系…...

【蓝桥杯集训·每日一题】AcWing 3696. 构造有向无环图
文章目录一、题目1、原题链接2、题目描述二、解题报告1、思路分析2、时间复杂度3、代码详解三、知识风暴拓扑排序一、题目 1、原题链接 3696. 构造有向无环图 2、题目描述 给定一个由 n 个点和 m 条边构成的图。 不保证给定的图是连通的。 图中的一部分边的方向已经确定&#…...
国内vs国外:外贸建站该如何选择?
外贸建站找国内还是国外? 答案是:国内。 随着互联网的发展,越来越多的企业开始意识到在网络上进行商业活动的重要性。 其中,建立一个专业的外贸网站是企业在国际市场上拓展业务的关键。 然而,对于选择国内还是国外…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...
