【数据结构】树
一.二叉树的基本概念和性质:
1.二叉树的递归定义:
二叉树或为空树,或是由一个根结点加上两棵分别称为左子树和右子树的、互不相交的二叉树组成
2.二叉树的特点:
(1)每个结点最多只有两棵子树,即不存在结点度大于2的结点
(2)子树有左右之分,不能颠倒。
3.满二叉树:
深度为k,且有个结点的二叉树。
(1)每一层上结点数都达到最大。
(2)度为1的结点数
4.完全二叉树:
深度为k,结点数为n的二叉树,当且仅当每个结点的编号都与相同深度的满二叉树中从1到n的结点一一对应时,称为完全二叉树。
(1)完全二叉树的任意结点,左子树的高度-右子树的高度=0或1
5.二叉树的性质:
1)在二叉树的第i层,至多有个结点。
2)深度为k的二叉树上至多含有个结点。
3)
证明如下:
二叉树中全部结点数
除根结点外,每个结点必有一个直接前驱,即一个分支
(1度结点必有1个直接后继,2度结点必有2个直接后继)
即:
叶子数=2度结点数+1
4)具有n个结点的完全二叉树的深度为
5)
对有n个结点的完全二叉树的结点按层序编号,则对于任一结点i,有:
- 如果i=1,则结点i是二叉树的根,无双亲;如果i>1,则其双亲是i/2
- 如果2i>n,则结点i无左孩子;如果
,则其左孩子是2i
- 如果2i+1>n,则结点i无右孩子;如果
,则其右孩子是2i+1
例题:
设一棵完全二叉树具有1000个结点,则它有489个叶子结点,有488个度为2的结点,有1个结点只有非空左子树,有0个结点只有非空右子树。
二.二叉树、树以及森林的存储结构
1.二叉树的顺序存储结构
用一组地址连续的存储单元,以层序顺序存放二叉树的数据元素,结点的相对位置蕴含着结点之间的关系。
问:顺序存储后能否复原成唯一对应的二叉树形状?
若是完全二叉树则可以完全复原,下标值为i的双亲,左孩子为2i,右孩子为2i+1。
而对于一般的二叉树的存储,将其先补成完全二叉树,然后按照完全二叉树的顺序存储方式进行存储,而新补上的结点只占位置,不存放数据元素。
对于一般二叉树的顺序存储,如果是斜树,则会浪费很多的存储空间,而且插入删除不便。
2.二叉树的链式存储结构
有一个指向根的指针root
二叉链表:2个链分别存放左孩子和右孩子。
三叉链表:2个链分别存放左孩子和右孩子另外一个指向双亲。
线索链表:用空链域存放前驱或后继。
2.1 二叉链表:
结点结构:
| lchild | data | rchild |
typedef struct BiTreeNode{DataType data;struct BiTreeNode *lchild,*rchild;
}BiTreeNode,*BiTree;2.2 三叉链表:
结点结构:
| parent | lchild | data | rchild |
typedef struct BiTreeNode{DataType data;struct BiTreeNode *lchild,*rchild,*parent;
}BiTreeNode,*BiTree;3.树和森林的存储结构
3.1 树的双亲表示法
对于一个结点来说,双亲是一定的。
typedef struct PTNode{DataType data;int parent;
}PTNode;
typedef struct PTree{PTNode nodes[MAX_SIZE];int r,n;
}PTree;3.2 树的孩子表示法
对于一个结点来说,孩子的数量是不一定的,为了整体元素结构的一致性,采用存储地址的方法。
typedef struct CTNode{int child;struct CTNode *next;
}CTNode;typedef struct CTBox{DataType data;CTNode *firstchild;
}CTBox;
typedef struct CTree{CTBox nodes[MAX_SIZE];int n,r;
}CTree;3.3 树的双亲孩子表示法
结点结构变为
| data | parent(下标) | 指向第一个孩子的指针 |
3.4 树的孩子兄弟表示法
typedef struct CSNode{datatype data;struct CSNode *firstchild,*rightsib;
}CSNode;三.二叉树、树及森林的基本操作
1.二叉树的遍历
顺着某一条搜索路径寻访二叉树中的结点,使得每个结点均被访问一次,且仅被访问一次。
1.1 先序遍历:
根、左、右。
若二叉树非空,则:
1)访问根结点
2)先序遍历左子树
3)先序遍历右子树
typedef struct BiNode{int data;struct BiNode *rchild,*lchild;
}BiNode;
void preOrder(BiNode *root){if(root){cout<<root->data;preOrder(root->lchild);preOrder(root->rchild);}
}1.2 中序遍历:
左、根、右。
若二叉树非空,则:
1)中序遍历左子树
2)访问根结点
3)中序遍历右子树
void inOrder(BiNode *root){if(root){inOrder(root->lchild);cout<<root->data;inOrder(root->rchild);}
}中序遍历的非递归算法:
1.初始化栈,将根结点入栈。
2.如果栈空则结束(空树或所有结点处理完毕),否则进入下一步。
3.p指向栈顶元素,如果p不空,则左孩子入栈,直到左孩子为空。
4.如果栈不空,则出栈,输出该结点,再将其右孩子入栈。以该结点为本子树的根,转步骤2继续。
void InOrder(BiNode *root){stack <BiNode*> s;BiNode* p=root;s.push(p);while(!s.empty()){while(p->lchild){//走到最左边p=p->lchild;s.push(p);}p=s.top();//弹栈s.pop();cout<<p->data;if(p->rchild){s.push(p->rchild);}}
}1.3 后序遍历:
左、右、根。
若二叉树非空,则:
1)后序遍历左子树
2)后序遍历右子树
3)访问根结点
void postOrder(BiNode *root){if(root){postOrder(root->lchild);postOrder(root->rchild);cout<<root->data;}
}1.4 层次遍历:
从上到下、从左到右。
初始化队列,根结点入队列。
如果队列不空,则出队列并访问该结点;该结点左孩子入队,右孩子入队;如果队列为空,则层次遍历结束。
void levelOrder(BiNode *root){queue <BiNode*> s;BiNode* p=root;s.push(p);while(!s.empty()){p=s.front();s.pop();cout<<p->data;if(p->lchild){s.push(p->lchild);}if(p->rchild){s.push(p->rchild);}}
}1.5 对遍历的分析:
从前面的三种遍历算法可以知道,如果将输出语句抹掉,从递归的角度看,这三种算法是完全相同的,或者说这三种遍历算法的访问路径是相同的,只是访问结点的时机不同。
从虚线的出发点到终点的路径上,每个结点经过三次。
- 第一次经过时访问=先序遍历
- 第二次经过时访问=中序遍历
- 第三次经过时访问=后序遍历
1.6 二叉树遍历算法的应用举例:
1.6.1 表达式树:
算数表达式可以表示为一棵二叉树 中缀表达——对树进行中序遍历即可得到表达式。
- 前缀表达式:不含括号的算数表达式,将运算符写在前面,操作数写在后面。
- 中缀表达式:操作符以中缀形式处于操作数中间。
- 后缀表达式:不包含括号,运算符放在两个运算对象的后面,所有的计算按运算符出现的顺序,严格的从左到右进行(不再考虑运算符的优先次序)
表达式树的构建:(即:给出一个中序序列,构建出这棵树)
顺序扫描中缀表达式 明确:左子树的优先级高
- 当扫描到的是运算数:先检查当前的表达式树是否存在。如果不存在,则表示扫描到的是第一个运算数,将它作为树根。如果树存在,则将此运算数作为前一运算符的右孩子。
- 如果扫描到的是+或-:将它作为根结点,原来的树作为它的左子树。
- 如果扫描到的是*或/:则与根结点进行比较。如果根节点也是*或/,则根结点应该先执行,于是,将当前的运算符作为根结点,原来的树作为左子树。如果根结点是+或-,则当前运算符应该先运算,于是将它作为右子树的根,原来的右子树作为它的左子树。
在遇到运算数时,如何知道它前面的运算符是谁?这只需要判别根结点有没有右孩子。如果没有右孩子,则运算数是根节点的右运算数,否则就是根结点右孩子的右运算数。
1.6.2 由先序和中序遍历序列建立二叉树:
可以唯一的确定一棵二叉树。
void PreInorder(char preorder[],char inorder[],int first1,int end1,int first2,int end2,BiNode *t){//先序序列从first1到end1,中序序列从first2到end2,建立一棵二叉树放在t中int m;t=new BiNode;t->data=preorder[first1];//二叉树的根m=first2;while(inorder[m]!=preorder[first1]){//在中序序列中定位根结点的位置++m;}//建立左子树if(m==first2){//左子树为空t->lchild=NULL;}else{PreInorder(preorder, inorder, first1+1, first1+m-first2, first2, m-1, t->lchild);}//建立右子树if(m==end2){//右子树为空t->lchild=NULL;}else{PreInorder(preorder, inorder, first1+m+1-first2, end1, m+1, end2, t->rchild);}
}
void CreateBiTree(char preorder[],char inorder[],int n,BiNode *root){if(n<=0){root=NULL;}else{PreInorder(preorder, inorder, 0, n-1, 0, n-1, root);}
}1.6.3 二叉树中叶子结点的统计:
先序(中序或后序)遍历二叉树,在遍历过程中查找叶子节点,将算法中“访问结点”的操作改为:判定是否为叶子结点。
叶子结点:左右孩子均为空。
1.6.4 二叉树的深度:
空树:深度=0;
左右子树为空:深度=1;
其他:深度等于1+max(左子树深度,右子树深度)
int get_depth(BiNode *t){if(t==NULL){return 0;}else if(t->lchild==NULL&&t->rchild==NULL){return 1;}else{int depth;int depth1=get_depth(t->lchild);int depth2=get_depth(t->rchild);depth=max(depth1,depth2);return depth;}
}2.树和森林的基本操作
2.1 树以及森林和二叉树的相互转换
1)树->二叉树
兄弟加线,每一个结点只保留与第一个孩子的连线,再进行旋转。
树转换成的二叉树,其根结点的右子树一定为空。
想要有右子树,就必须要有兄弟。将兄弟作为右子树。
2)二叉树->树
结点与其右子树、右子树的右子树加线,去掉结点与右子树的连线,再进行旋转。
3)森林->二叉树
将森林中的每一棵树都先转化为二叉树,再令第i棵树作为第i-1棵树的右子树。
4)二叉树->森林
断开根结点与右子树的关系,再将右子树作为新树,依次断开根结点与右子树的关系,直至右子树为空,得到了多棵二叉树。
再将这些二叉树转化为树。
2.2 树的遍历
- 先序遍历
- 后序遍历
- 层次遍历
没有中序遍历是因为树不分左右子树
2.3 森林的遍历
- 先序遍历:先序遍历每一棵树
- 中序遍历:后序遍历每一棵树
四.二叉树的变形
1.二叉排序树(BST)
对于二叉排序树的插入和删除操作:我们需要改变指针指向的地址,而在函数中传递指针,只能够改变指针指向的内容,所以要传递指针的引用。
1.1 定义(具有递归性质):
二叉排序树或是一颗空树,或是一棵具有以下性质的树
(1)若它的左子树不空,则它左子树上所有结点的值均小于根结点的值。
(2)若它的右子树不空,则它右子树上所有结点的值均大于根结点的值。
(3)它的左右子树都是二叉排序树
1.2 二叉排序树的查找:
在二叉排序树中查找给定k值的过程是:
1)若root是空树,则查找失败
2)若k=root->data,则查找成功,否则
3)若k<root->data,则在root的左子树上查找;否则
4)在root的右子树上查找。
上述过程一直持续到k被找到或者待查找的子树为空。如果待查找的子树为空,则查找失败。
只需要查找两个子树之一。
BiNode* search(BiNode *root,int key){if(root==NULL){return NULL;}else{while(key!=root->data){if(key>root->data){root=root->rchild;}else if(key<root->data){root=root->lchild;}else{break;}}return root;}
}1.3 二叉排序树的插入:
若二叉排序树为空树,则新插入的结点为新的根结点;否则新插入的结点必为一个新的叶子结点,其插入位置由查找过程得到。
void insert(BiNode *&root,int key){BiNode *p;if(root==NULL){p=new BiNode;p->data=key;p->lchild=NULL;p->rchild=NULL;}else{if(key<root->data){insert(root->lchild, key);}else{insert(root->rchild,key);}}
}二叉排序树的构造:
BiSortTree::BiSortTree(int array[],int n){root=NULL;for(int i=0;i<n;i++){insertBST(root, array[i]);}
}二叉排序树构造算法总结:
1)一个无序序列可以通过构造一棵二叉排序树而变成一个有序序列2)每次插入的新结点都是二叉排序树上新的叶子结点
3)找到插入位置后,不必移动其它结点,仅需修改某个结点的指针
4)在左子树/右子树的查找过程与在整棵树上查找过程相同
5)新插入的结点没有破坏原有结点之间的关系
注:
此处函数参数为指针的引用类型
1)只传指针的话,只能改变指针最初的指向的内容,而不能够改变指针所指向的地址。
2)而采用指针的引用,实际上改变指针,就改变了指针指向的地址。
3)这样做,还能够直接链接起根结点和孩子之间的指针关系。(bt->lchild/rchild 就被赋值为下一级函数所开辟出空间的地址)
1.4 二叉排序树的删除:
在二叉排序树上删除某个结点之后,仍然保持二叉排序树的特性。
1)被删除的结点是叶子
删除该结点,并将该结点的双亲的孩子指针域赋值为空
2)被删除的结点只有左子树或只有右子树
将双亲结点相应的指针域的值指向被删除结点的左/右孩子
3)被删除的结点既有左子树,又有右子树
以其左子树的最大值或右子树的最小值来代替该结点
以其前驱替代,然后再删除前驱结点
void deleteNode(BiNode *&bt){BiNode *p=bt;if(bt->lchild==NULL&&bt->rchild==NULL){//叶子结点bt=NULL;//该结点的双亲结点的相应孩子指针被赋值为空delete p;//返回时,其双亲的左右孩子指针均被赋值为NULL}if(bt->lchild==NULL){//该结点的左孩子为空,只有右子树bt=bt->rchild;delete p;}if(bt->rchild==NULL){//该结点的右孩子为空,只有左子树bt=bt->lchild;delete p;}else{//左右子树均存在,选取其前驱作为新的根结点BiNode *parent=bt,*pre=bt->lchild;while(pre->rchild){//找到左子树值最大的结点,parent保存这个结点的双亲结点parent=pre;pre=pre->rchild;}bt->data=pre->data;//用该结点的直接前驱替代该结点,并删除该结点的直接前驱if(parent==bt){parent->lchild=pre->lchild;}else{parent->rchild=NULL;}delete pre;}
}二叉排序树的性能取决于二叉树的形状
2.平衡二叉树
2.1 定义:
平衡二叉树或者是一颗空树,或者是具有下列性质的二叉树:
- 是一棵二叉排序树
- 并且任何结点的左右子树的深度之差不超过1
2.2 构造平衡二叉树:
在插入过程中,采用平衡旋转技术。
1)平衡因子BF(Balance Factor):
左子树高度 - 右子树高度的值
平衡因子的绝对值大于1,就需要进行调整。
2)最小不平衡子树:
距离插入结点最近的,且BF的绝对值大于1的结点。
旋转只需要纠正最小不平衡子树即可。
3)右旋:
- 旧根结点为新根结点的右子树
- 新根结点的右子树(如果存在)为旧根结点的左子树
4)左旋:
- 旧根结点为新根结点的左子树
- 新根结点的左子树(如果存在)为旧根结点的右子树
2.3 四种类型的旋转
1)LL型
2)RR型
3)LR型
最小不平衡子树根结点左子树先左旋,最小不平衡子树再右旋
4)RL型
最小不平衡子树根结点右子树先右旋,最小不平衡子树再左旋
3.最优树——哈夫曼树
3.1哈夫曼编码
1)前缀码:
对每一个字符规定一个0,1串作为其代码,并要求任一字符的代码都不是其他字符代码的前缀。
2)前缀码的平均码长:
每个字符频率乘以该字符编码的bit数之和。
3)最优前缀码:
寻找最小的前缀码的平均码长。
4)最优树:
称树的带权路径长度最短的一类树为“最优树”。
3.2 哈夫曼树的构造
(1)初始化:
由给定的 n个权值构造n棵只有一个根结点的二叉树,从而得到一个二叉树集合。(2)选取与合并:
在二叉树集合中选取根结点的权值最小的两颗二叉树分别作为左、右子树构造一颗新的二叉树,这颗新的二叉树的根结点的权值为其左、右子树根结点的权值之和。(3)删除与加入
在二叉树集合中删去作为左、右子树的二叉树,并将新建立的二叉树加入到二叉树结合中。(4)重复
重复(2)(3)两步,直到二叉树集合中只剩下一颗二叉树。
哈夫曼树的左右子树可以进行交换。
有n个叶子结点的哈夫曼树有2n-1个结点。
3.3 哈夫曼算法的实现:
1)存储结构:
| weight | lchild | rchild | parent |
由于有n个叶子结点的哈夫曼树有2n-1个结点,设置数组长度为2n-1。
2)伪代码:
1.数组huffTree初始化:
所有元素结点的双亲、左右孩子都置为-1.
2.权值给定:
数组huffTree的前n个元素的权值给定
3.进行n-1次合并:
3.1 在二叉树集合中选取两个权值最小的根结点,其下标为i1,i2
3.2 将二叉树i1,i2合并为一棵新的二叉树
struct element{int weight;int lchild,rchild,parent;
};
void select(struct element huffTree[],int k,int &i1,int &i2){for(int i=0;i<k;i++){//初始化i1,i2if(huffTree[i].parent==-1){i1=i2=i;break;}}for(int i=0;i<k;i++){if(huffTree[i].parent==-1&&huffTree[i].weight<huffTree[i1].weight){i1=i;}}for(int i=0;i<k;i++){if(huffTree[i].parent==-1&&i!=i1&&huffTree[i].weight<huffTree[i2].weight){i2=i;}}
}
void huffmanTree(struct element huffTree[],int w[],int n){int i1,i2,i;for(i=0;i<2*n-1;i++){huffTree[i].parent=huffTree[i].lchild=huffTree[i].rchild=-1;}for(i=0;i<n;i++){huffTree[i].weight=w[i];}for(i=n;i<2*n-1;i++){select(huffTree, i, i1, i2);huffTree[i].weight=huffTree[i1].weight+huffTree[i2].weight;huffTree[i1].parent=i;huffTree[i2].parent=i;huffTree[i].lchild=i1;huffTree[i].rchild=i2;}
}4.堆排序
4.1 堆的定义:
堆通常是一个可以被看作一棵完全二叉树的数组对象。
每个结点的值都小于或等于其左右孩子结点的值(称为小根堆)
或每个结点的值都大于或等于其左右孩子结点的值(称为大根堆)
特点:
1.大根堆的根结点是所有结点中值最大的结点。
2.较大结点靠近根节点,但不绝对。
3.每次创建一个堆,都使数据基本有序。
4.2 堆排序的思想:
首先,将待排序的记录序列构造成一个堆(大根堆),此时,选出了堆中所有记录的最大者,然后将它从堆中移走,并将剩余的记录再调整成堆,这样,又找出了次大的记录,以此类推,直到堆中只有一个记录。
4.3 堆的存储:
将堆用顺序结构存储,则堆就对应了一组序列。
根据完全二叉树的性质:
结点i的双亲结点编号为i/2,左孩子为2i,右孩子为2i+1
4.4 堆调整:
在一棵完全二叉树中,根结点的左右子树均是堆,如何调整根结点,使整个完全二叉树成为一个堆?
建立堆,从下向上调整;调整堆时,从上向下处理。
首先,根和他两个孩子中较大的那个比较,如果根比较大,不做处理;如果根比较小,则交换,交换后,再去看交换的结果是否影响下面的堆。
4.5 如何处理堆顶元素?
堆顶就是r[1]。
第k次处理堆顶,就是将堆顶记录r[1]与r[n-k+1]交换。
4.6 代码:
void sift(int r[],int k,int end){//当前处理的根结点的编号为k,堆中最后一个结点的编号为kint i=k;int j=2*i;int temp;while(j<=end){if(j<end&&r[j]<r[j+1]){//找到左右孩子中较大的那个j++;}if(r[i]<r[j]){temp=r[i];r[i]=r[j];r[j]=temp;}i=j;j=2*i;}
}
void heapsort(int r[],int n){//初始化,得到一个初始堆for(int k=n/2;k>=1;k--){sift(r,k,n);}for(int k=1;k<n;k++){//最大的元素往后挪,堆逐渐缩小r[0]=r[1];r[1]=r[n-k+1];r[n-k+1]=r[0];sift(r,1,n-k);}
}时间复杂度:
不稳定排序
相关文章:
【数据结构】树
一.二叉树的基本概念和性质: 1.二叉树的递归定义: 二叉树或为空树,或是由一个根结点加上两棵分别称为左子树和右子树的、互不相交的二叉树组成 2.二叉树的特点: (1)每个结点最多只有两棵子树࿰…...
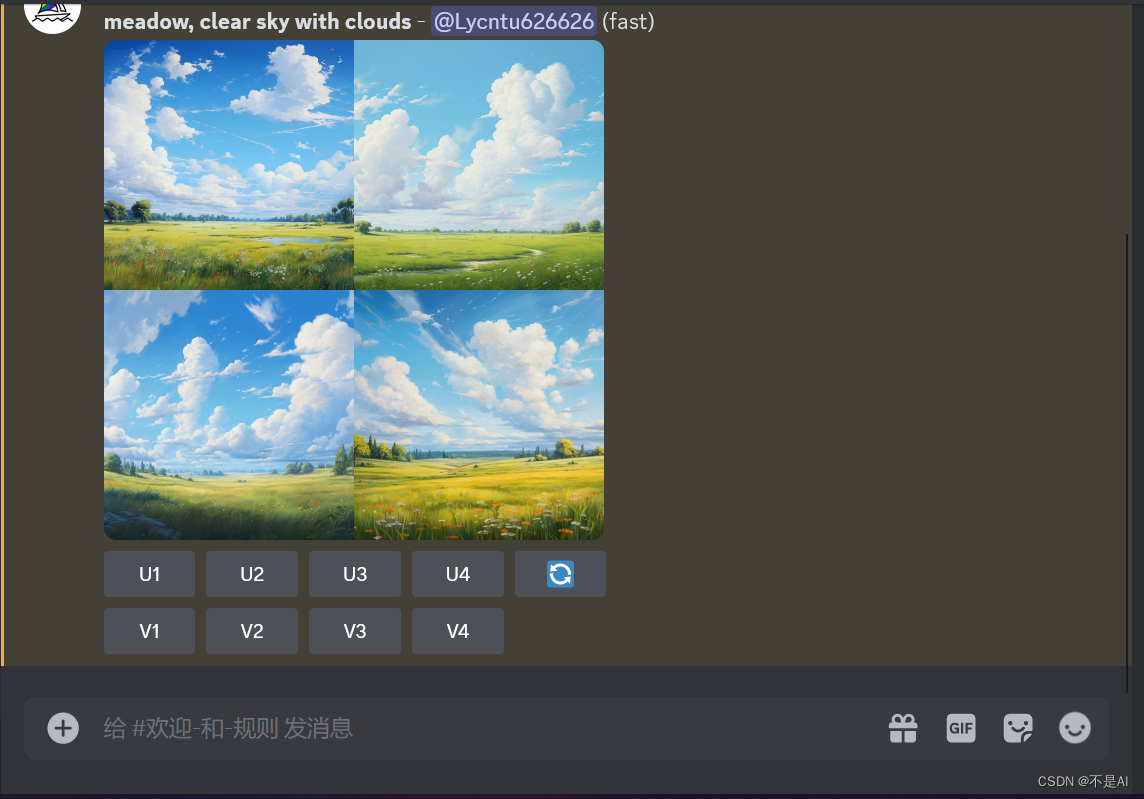
【Midjourney】AI绘画新手教程(一)登录和创建服务器,生成第一幅画作
一、登录Discord 1、访问Discord官网 使用柯學尚网(亲测非必须,可加快响应速度)访问Discord官方网址:https://discord.com 选择“在您的浏览器中打开Discord” 然后,注册帐号、购买套餐等,在此不做缀述。…...

对比 PyTorch 和 TensorFlow:选择适合你的深度学习框架
目录 引言 深度学习在各行业中的应用 PyTorch 和 TensorFlow 简介 PyTorch:简介与设计理念 发展历史和背景 主要特点和设计理念 TensorFlow:简介与设计理念 发展历史和背景 主要特点和设计理念 PyTorch 和 TensorFlow 的重要性 Pytorch对比Te…...

Oracle笔记-查看表已使用空间最大空间
目前以Oracle18c为例,主要是查这个表USER_SEGMENTS。 在 Oracle 18c 数据库中,USER_SEGMENTS 是一个系统表,用于存储当前用户(当前会话)拥有的所有段的信息。段是 Oracle 中分配存储空间的逻辑单位,用于存…...

大数据HCIE成神之路之特征工程——特征选择
特征选择 1.1 特征选择 - Filter方法1.1.1 实验任务1.1.1.1 实验背景1.1.1.2 实验目标1.1.1.3 实验数据解析1.1.1.4 实验思路 1.1.2 实验操作步骤 1.2 特征选择 - Wrapper方法1.2.1 实验任务1.2.1.1 实验背景1.2.1.2 实验目标1.2.1.3 实验数据解析1.2.1.4 实验思路 1.2.2 实验操…...

python 正则-常见题目
1、邮箱 print(re.findall(r[\w-][\w-]\.[\w-], weidianqq.com))2、身份证号 xxxxxx yyyy MM dd 375 0 十八位 print(re.findall(r(?:18|19|(?:[23]\d))\d{2}, 2010)) # 年print(re.findall(r(?:0[1-9])|10|11|12, 11)) # 月print(re.findall(r(?:[0-2][1-9])|10|20|30|3…...

解析:Eureka的工作原理
Eureka是Netflix开源的一个基于REST的的服务发现注册框架,它遵循了REST协议,提供了一套简单的API来完成服务的注册和发现。Eureka能够帮助分布式系统中的服务提供者自动将自身注册到注册中心,同时也能够让服务消费者从注册中心发现服务提供者…...

RecyclerView 与 ListView 区别和使用
前置知识:ListView基本用法与性能提升 RecyclerView 与 ListView 区别 RecyclerView 需要设置布局(LinearLayoutManager、GridLayoutManager、StaggeredGridLayoutManager) recyclerView?.layoutManager LinearLayoutManager(activity) …...

力扣232. 用栈实现队列
题目 请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty): 实现 MyQueue 类: void push(int x) 将元素 x 推到队列的末尾int pop() 从队列的开头移除并返回元素int peek() 返回队列开…...
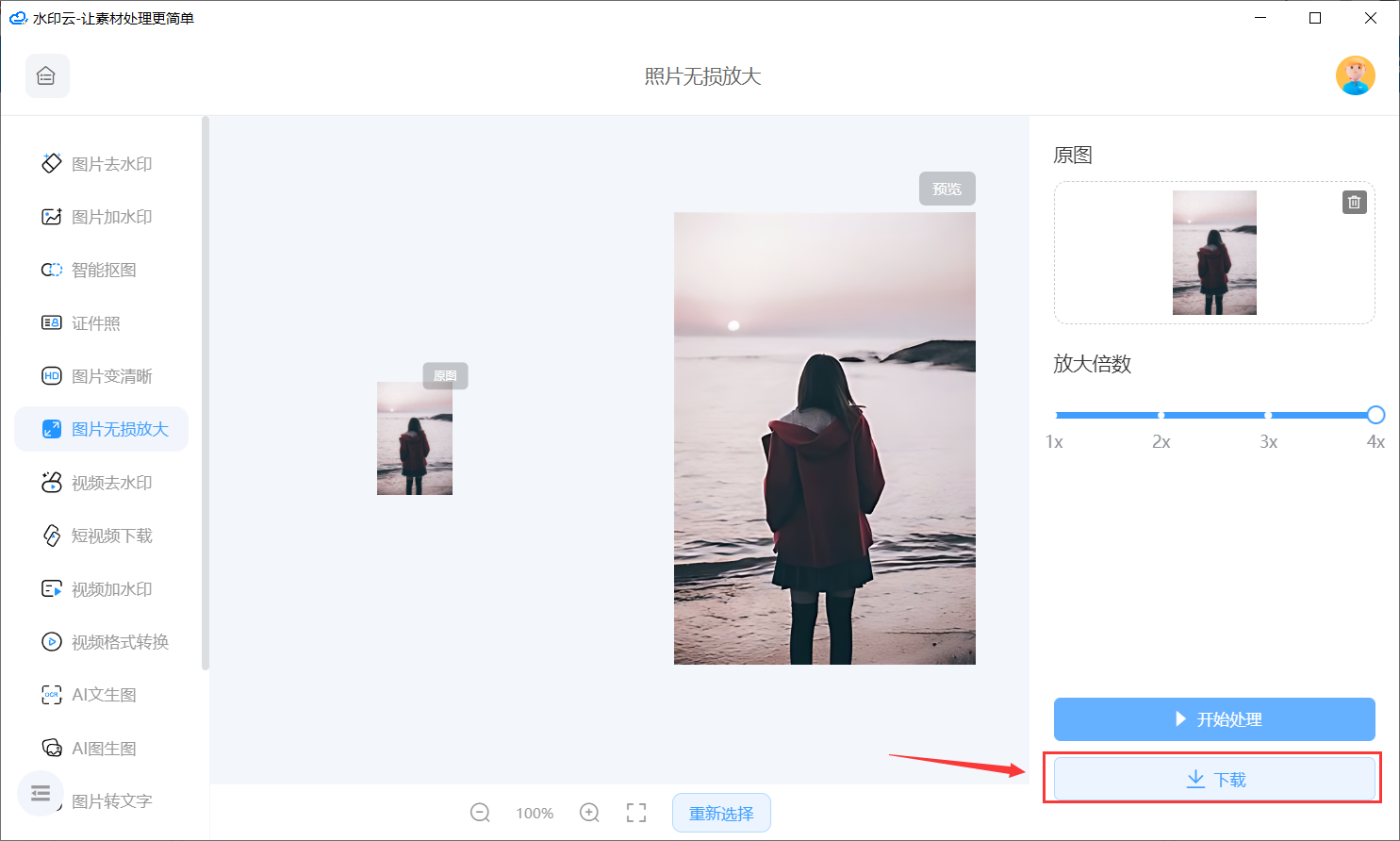
这个方法可以让你把图片无损放大
随着数字技术的不断发展,照片无损放大已经成为了摄影领域中的一项重要技术。照片无损放大能够让摄影师在不损失细节和画质的情况下,将照片放大到更大的尺寸,从而让观众能够更加清晰地欣赏到照片中的每一个细节。 今天推荐的这款软件主要是通…...

Springboot整合Elastic-job
一 概述 Elastic-Job 最开始只有一个 elastic-job-core 的项目,定位轻量级、无中心化,最核心的服务就是支持弹性扩容和数据分片!从 2.X 版本以后,主要分为 Elastic-Job-Lite 和 Elastic-Job-Cloud 两个子项目。esjbo官网地址 Ela…...
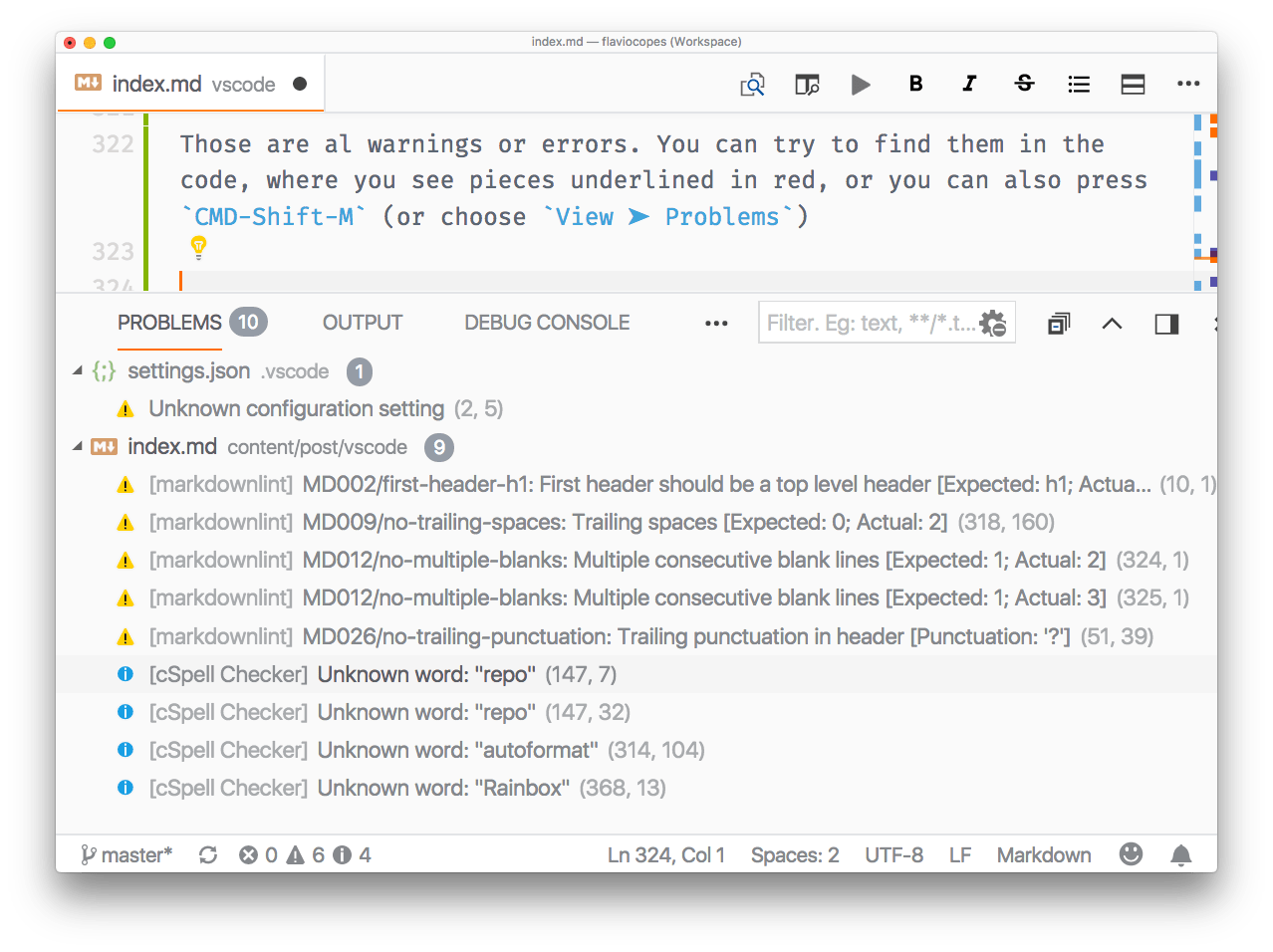
VsCode的介绍和入门
目录 编辑 介绍 我应该切换到 VS Code 吗?为什么? 入门 Explorer 搜索 源代码控制 调试器 扩展 终点站 命令面板 主题 定制化 不错的配置选项 最适合编码的字体 工作空间 编辑 智能感知 代码格式化 错误和警告 键盘快捷键 键位图…...

C++:自创小游戏
欢迎来玩,每次都有不一样的结果。 长达142行。 #include<bits/stdc.h> #include<windows.h> #define random(a,b) (rand()%(b-a1)a) using namespace std; int main(){int n;cout<<"输1~10,越小越好,不告诉你有什么用,当然也可…...

AIGC带给开发者的冲击
未来会有两种开发者,一种是会使用AIGC工具的开发者另一种是不会使用AIGC的开发者,AIGC的出现提高了开发效率和代码质量,对开发者意味着需要不断学习和适应新的技术和工作范式,开发者可以把更多的精力放在高级抽象的定义以及更高维…...
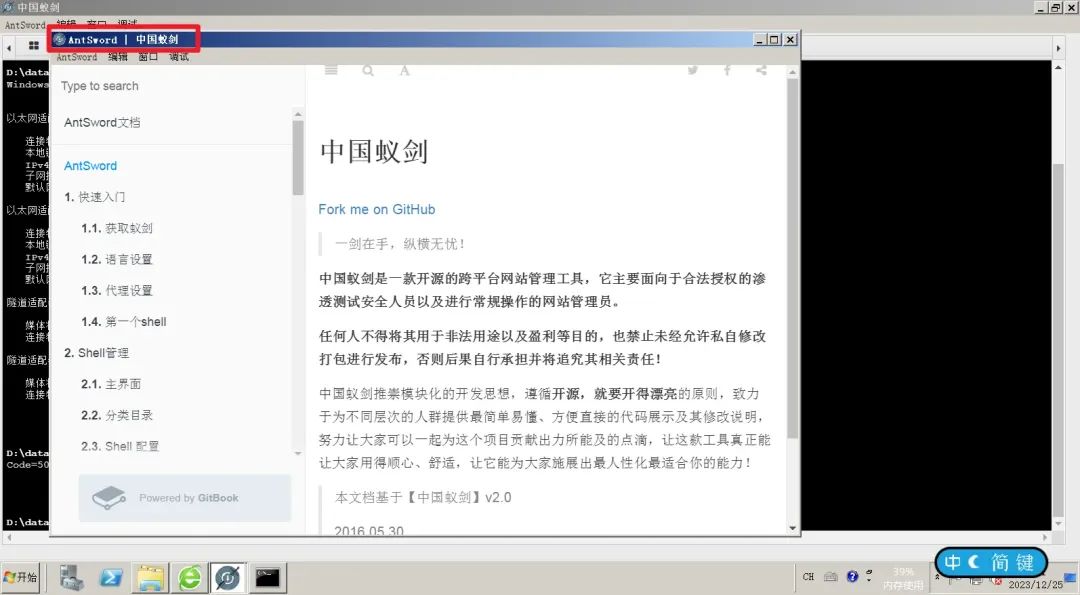
利用蚁剑钓鱼上线CS
前言 中国蚁剑使用Electron构建客户端软件,Electron实现上用的是Node.js,并且Node.js能执行系统命令,故可以利用蚁剑的webshell页面嵌入js来直接执行命令,进而钓鱼来上线CS。(类似Goby,Goby也是使用Electr…...

宣传照(私密)勿转发
精美的海报通常都是由UI进行精心设计的,现在有100 件商品需要进行宣传推广,如果每个商品都出一张图显然是不合理的,且商品信息各异。因此需要通过代码的形式生成海报。对此,我也对我宣传一波,企图实现我一夜暴富的伟大…...

【Spring】19 AOP介绍及实例详解
文章目录 1. 定义1)什么意思呢?2)如何解决呢? 2. 基本概念1)切面(Aspect)2)切点(Pointcut)3)通知(Advice)4)连…...
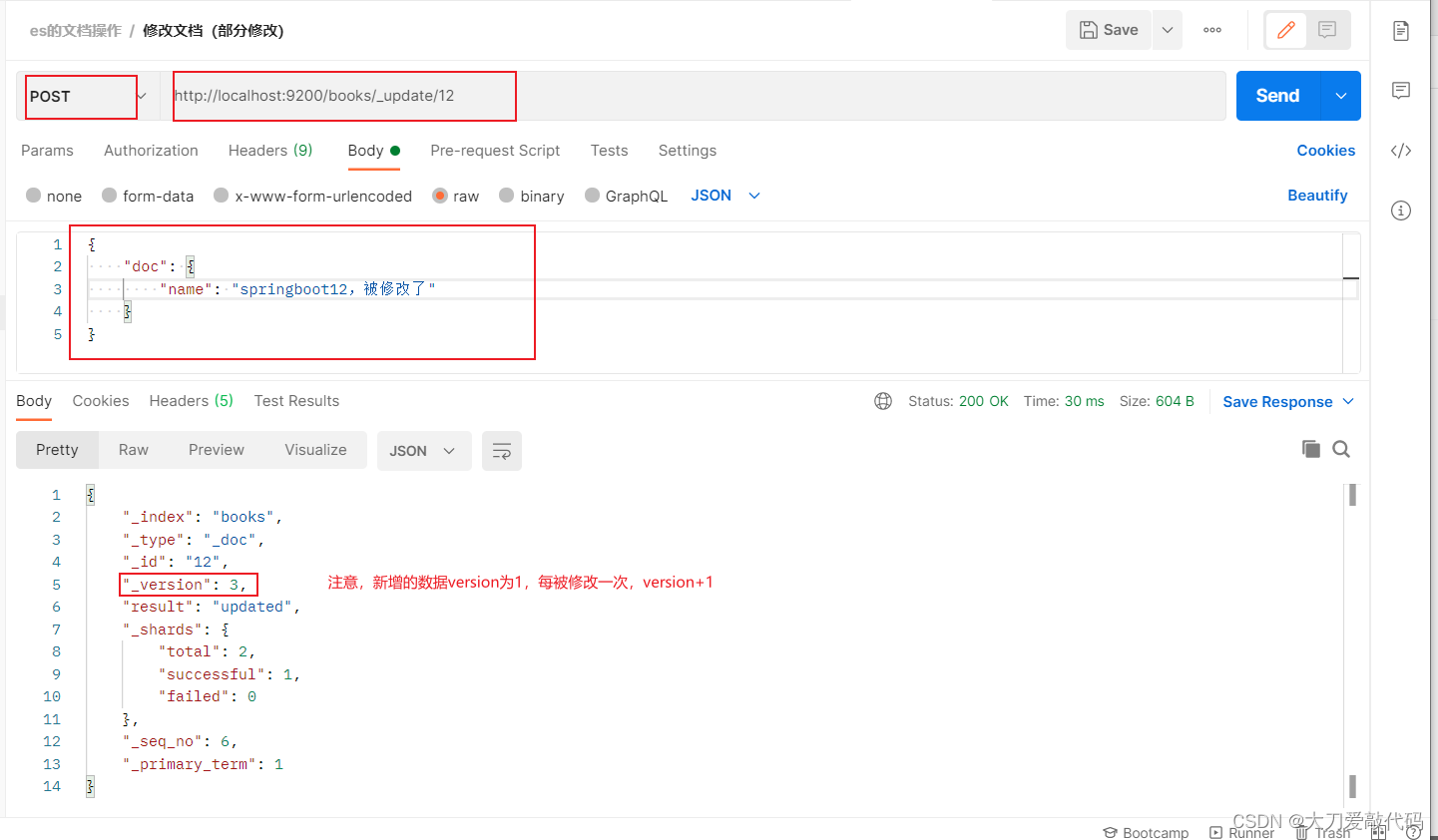
ES(Elasticsearch)的基本使用
一、常见的NoSQL解决方案 1、redis Redis是一个基于内存的 key-value 结构数据库。Redis是一款采用key-value数据存储格式的内存级NoSQL数据库,重点关注数据存储格式,是key-value格式,也就是键值对的存储形式。与MySQL数据库不同࿰…...

【JVM面试题】Java中的静态方法为什么不能调用非静态方法
昨晚京东大佬勇哥在群里分享了一道他新创的JVM面试题,我听完后觉得还挺有意思的,分享给大家 小佬们先别急着看我的分析,先自己想想答案 你是不是想说 因为静态方法是属于类的,而非静态方法属于实例对象 哈,有人这样回答…...

对‘float16_t’的引用有歧义
float16_t 是一个半精度浮点数类型,通常在一些需要高性能和低精度的场合被使用。 如果加了using namespace cv;后,OpenCV库中也有一个名为float16_t的类型定义,与最初的float16_t存在冲突,导致编译失败。 为了解决这个问题&#…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...
