数模学习day06-主成分分析
主成分分析(Principal Component Analysis,PCA)主成分分析是一种降维算法,它能将多个指标转换为少数几个主成分,这些主成分是原始变量的线性组合,且彼此之间互不相关,其能反映出原始数据的大部分信息。一般来说当研究的问题涉及到多变量且变量之间存在很强的相关性时我们可考虑使用主成分分析的方法来对数据进行简化。
问题引出
在实际问题研究中,多变量问题是经常会遇到的。变量太多,无疑会增加分析问题的难度与复杂性,而且在许多实际问题中,多个变量之间是具有一定的相关关系的.
因此,人们会很自然地想到,能否在相关分析的基础上,用较少的新变量代替原来较多的旧变量,而且使这些较少的新变量尽可能多地保留原来变量所反映的信息?
事实上,这种想法是可以实现的,主成分分析方法就是综合处理这种问题的一种强有力的工具。
主成分分析是把原来多个变量划为少数几个综合指标的一种统计分析方法。从数学角度来看,这是一种降维处理技术
数据降维的作用
降维是将高维度的数据 (指标太多) 保留下最重要的一些特征,去除噪声和不重要的特征,从而实现提升数据处理速度的目的。
在实际的生产和应用中,降维在一定的信息损失范围内可以为我们节省大量的时间和成本。降维也成为应用非常广泛的数据预处理方法。
降维具有如下一些优点:
(1)使得数据集更易使用
(2)降低算法的计算开销
(3)去除噪声
(4)使得结果容易理解
例子

主成分分析的
思想


计算步骤




例题一
相关系数矩阵可以使用 corrcoef 这个函数计算


表中可以看到前三个主成分的累计贡献率达85.9%,因此可以考虑只取前面三个主成分,它们能够很好的概括原式变量。


例题二


这里为什么上半部分是空白的呢,是因为这个样本相关系数矩阵是一个对称的矩阵,所以是空白的。
然后就是计算相关的关键变量.

只要前两项贡献率已经达到了90%多了,所以后面的已经不重要了了。
然后重点就是如何解释主成分了。
由上表可知,前两个主成分的累计贡献率已高达93.7%,第一主成分F1在所有变量上有几乎相等的正载荷,可称为在径赛项目上的强弱成分第二主成分F2在各个指标上的载荷基本上逐个递减,反映了速度与耐力成绩的对比。
MATLAB代码实现
lambda = lambda(end:-1:1)
从大到小排序
V=rot90(V)';
disp(V)
将列的顺序调换
clear;clc
load data1.mat % 主成分聚类
% load data2.mat % 主成分回归% 注意,这里可以对数据先进行描述性统计
% 描述性统计的内容见第5讲.相关系数,该文章还未更新
[n,p] = size(x); % n是样本个数,p是指标个数%% 第一步:对数据x标准化为X
X=zscore(x); % matlab内置的标准化函数(x-mean(x))/std(x)%% 第二步:计算样本协方差矩阵
R = cov(X);%% 注意:以上两步可合并为下面一步:直接计算样本相关系数矩阵
R = corrcoef(x);
disp('样本相关系数矩阵为:')
disp(R)%% 第三步:计算R的特征值和特征向量
% 注意:R是半正定矩阵,所以其特征值不为负数
% R同时是对称矩阵,Matlab计算对称矩阵时,会将特征值按照从小到大排列哦
% eig函数的详解见第一讲层次分析法的视频
[V,D] = eig(R); % V 特征向量矩阵 D 特征值构成的对角矩阵%% 第四步:计算主成分贡献率和累计贡献率
lambda = diag(D); % diag函数用于得到一个矩阵的主对角线元素值(返回的是列向量)
lambda = lambda(end:-1:1); % 因为lambda向量是从小大到排序的,我们将其调个头
contribution_rate = lambda / sum(lambda); % 计算贡献率
cum_contribution_rate = cumsum(lambda)/ sum(lambda); % 计算累计贡献率 cumsum是求累加值的函数
disp('特征值为:')
disp(lambda') % 转置为行向量,方便展示
disp('贡献率为:')
disp(contribution_rate')
disp('累计贡献率为:')
disp(cum_contribution_rate')
disp('与特征值对应的特征向量矩阵为:')
% 注意:这里的特征向量要和特征值一一对应,之前特征值相当于颠倒过来了,因此特征向量的各列需要颠倒过来
% rot90函数可以使一个矩阵逆时针旋转90度,然后再转置,就可以实现将矩阵的列颠倒的效果
V=rot90(V)';
disp(V)%% 计算我们所需要的主成分的值
m =input('请输入需要保存的主成分的个数: ');
F = zeros(n,m); %初始化保存主成分的矩阵(每一列是一个主成分)
for i = 1:mai = V(:,i)'; % 将第i个特征向量取出,并转置为行向量Ai = repmat(ai,n,1); % 将这个行向量重复n次,构成一个n*p的矩阵F(:, i) = sum(Ai .* X, 2); % 注意,对标准化的数据求了权重后要计算每一行的和
end%% (1)主成分聚类 : 将主成分指标所在的F矩阵复制到Excel表格,然后再用Spss进行聚类
% 在Excel第一行输入指标名称(F1,F2, ..., Fm)
% 双击Matlab工作区的F,进入变量编辑中,然后复制里面的数据到Excel表格
% 导出数据之后,我们后续的分析就可以在Spss中进行。%%(2)主成分回归:将x使用主成分得到主成分指标,并将y标准化,接着导出到Excel,然后再使用Stata回归
% Y = zscore(y); % 一定要将y进行标准化哦~
% 在Excel第一行输入指标名称(Y,F1, F2, ..., Fm)
% 分别双击Matlab工作区的Y和F,进入变量编辑中,然后复制里面的数据到Excel表格
% 导出数据之后,我们后续的分析就可以在Stata中进行。然后就是解释
从上表可以看出,前两个和前三个主成分的累计贡献率分别达到80.6%和87.8%,第一主成分F1在所有变量(除在x2上的载荷稍偏小外)上都有近似相等的正载荷,反映了综合消费性支出的水平,因此第一主成分可称为综合消费性支出成分。第二主成分F2在变量x2上有很高的正载荷,在变量x4上有中等的正载荷,而在其余变量上有负载荷或很小的正载荷。可以认为这个主成分度量了受地区气候影响的消费性支出(主要是衣着,其次是医疗保健 )在所有消费性支出中占的比重(也可理解为一种消费倾向),第二主成分可称为消费倾向成分。第三主成分很难给出明显的解释,因此我们只取前面两个主成分。
数据可视化
求出R之后将它粘贴到Excel表格中
然后调整行高到 50 这样就是方形的了

然后再选择条件格式

再选择色阶

再修改管理规则

点击编辑规则
再修改成这样就基本上是一个颜色了

样子如下

颜色越深相关系数越强
主成分分析的滥用:主成分得分

主成分分析用于聚类

(1)主成分聚类 : 将主成分指标所在的F矩阵复制到Excel表格,然后再用Spss进行聚类
在Excel第一行输入指标名称(F1,F2, ..., Fm)
双击Matlab工作区的F,进入变量编辑中,然后复制里面的数据到Excel表格
导出数据之后,我们后续的分析就可以在Spss中进行。(2)主成分回归:将x使用主成分得到主成分指标,并将y标准化,接着导出到Excel,然后再使用Stata回归
Y = zscore(y); % 一定要将y进行标准化哦~
在Excel第一行输入指标名称(Y,F1, F2, ..., Fm)
分别双击Matlab工作区的Y和F,进入变量编辑中,然后复制里面的数据到Excel表格
导出数据之后,我们后续的分析就可以在Stata中进行。
spss聚类操作
首先找到系统聚类

移动指标

加上谱系图

画图


通过这个图就可以大致看出聚类的效果
主成分回归
用于解决多重共线性的问题
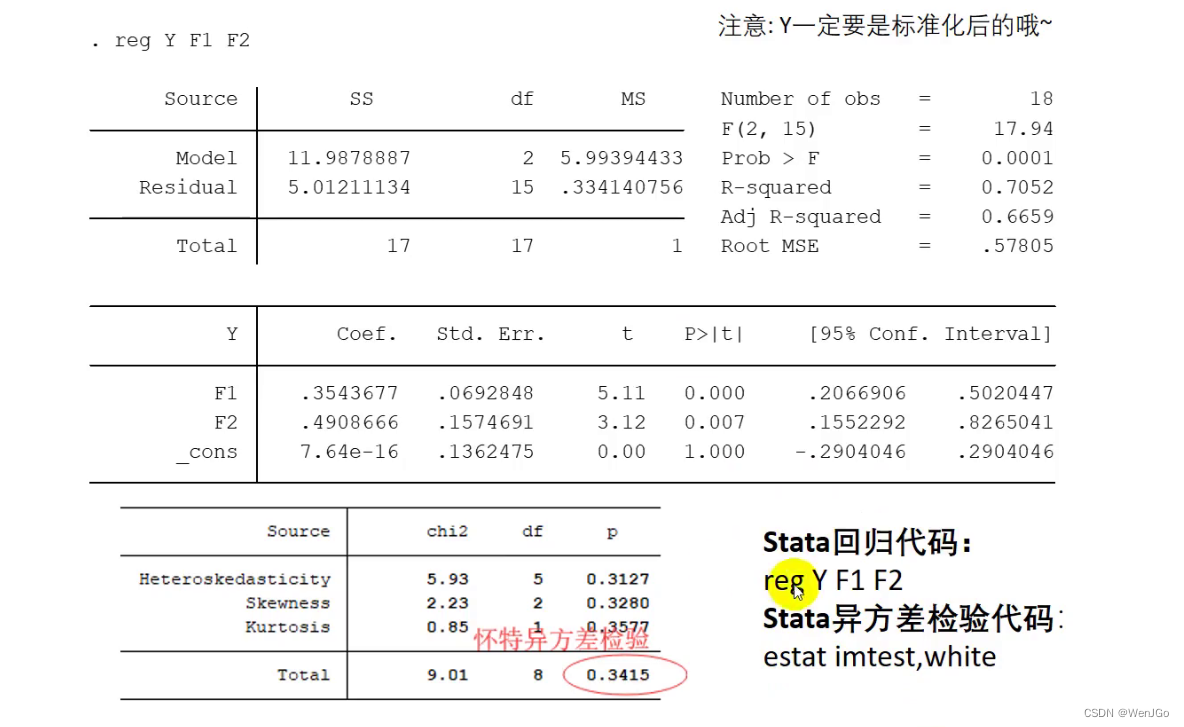
问题1: 之前学过逐步回归,逐步回归也可以用来解决多重共线性问题,我该用逐步回归还是今天学习的主成分分析呢?如果你能够很好的解释清楚主成分代表的含义,那么我建议你在正文中既用主成分分析,又用逐步回归 (多分析点没啥坏处只要你能保证你不分析错就行),如果你解释不清楚,那么还是用逐步回归吧。
问题2: 主成分回归后,需要将原来的变量带回到回归方程吗?我觉得没必要,要是你带回去了,那和普通的回归有什么区别呢。主成分的核心作用就是降维,带回去了维度也没降下来呀
相关文章:

数模学习day06-主成分分析
主成分分析(Principal Component Analysis,PCA)主成分分析是一种降维算法,它能将多个指标转换为少数几个主成分,这些主成分是原始变量的线性组合,且彼此之间互不相关,其能反映出原始数据的大部分信息。一般来说当研究的问题涉及到…...

Windows PowerShell的安全目标——安全警报
Windows PowerShell的安全目标——安全警报 1. 保证Shell安全 自从2006年年底PowerShell发布以来,微软在安全和脚本方面并没有取得很好的名声。毕竟那个时候,**VBScript和Windows Script Host(WSH)**是两个最流行的病毒和恶意软件的载体,…...
k8s笔记1- 初步认识k8s
k8s简介: kubernetes,俗称k8是,用于自动部署,扩缩和管理容器化应用程序的开源系统,它将组成应用程序的容器,组合成逻辑单元,便于管理和服务发现。 k8s的作用 自动化上线和回滚、存储编排…...
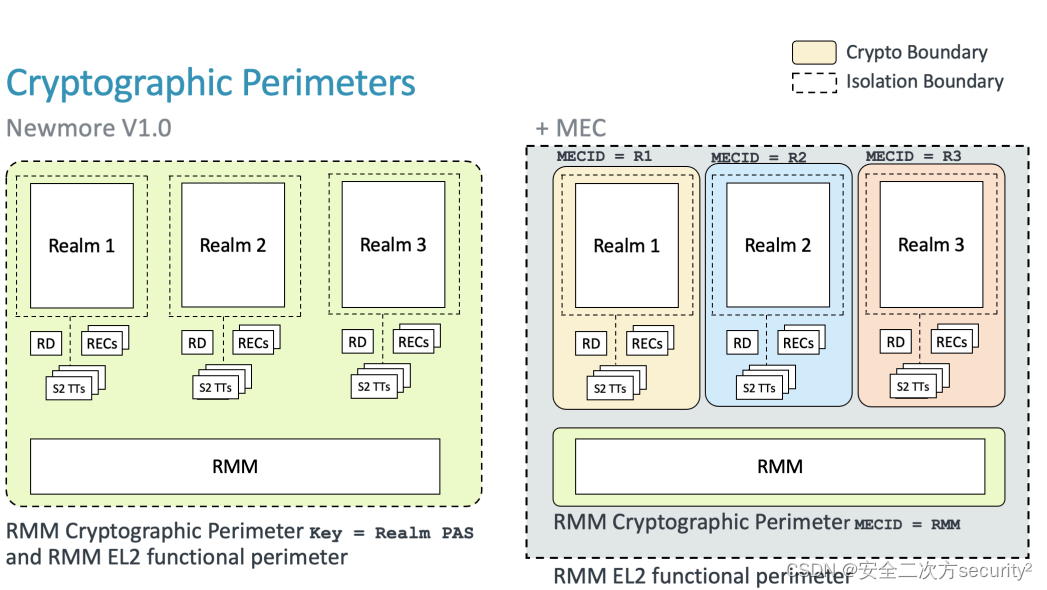
ARM CCA机密计算软件架构之内存加密上下文(MEC)
内存加密上下文(MEC) 内存加密上下文是与内存区域相关联的加密配置,由MMU分配。 MEC是Arm Realm Management Extension(RME)的扩展。RME系统架构要求对Realm、Secure和Root PAS进行加密。用于每个PAS的加密密钥、调整或加密上下文在该PAS内是全局的。例如,对于Realm PA…...

python基于flask实现一个文本问答系统
from flask import Flask, render_template, requestapp Flask(__name__)# 一个简单的问题-答案映射,实际中可以使用更复杂的存储结构(数据库等) qa_pairs {"什么是人工智能?": "人工智能是模拟人类智能的一种机…...

lambda表达式使用和示例
lambda表达式 什么是lambda 学习lamdba有两个结构十分关键,一个是lamdba自己,另一个是函数式接口 lamdba lamdba表达式本质上就是匿名方法,不能独立运行用于实现函数式接口定义的另一个方法,因此lamdba会产生一个匿名类lamdba…...
探索游戏多样性,范围伤害模式)
STM32学习笔记十八:WS2812制作像素游戏屏-飞行射击游戏(8)探索游戏多样性,范围伤害模式
前面我们的攻击手段比较单一,虽然已经分出了 EnemyT1 / EnemyT2 / EnemyT3, 但里面还是基本一样的。这回,我们尝试实现一些新的攻击方法,实现一些新的算法。 1、前面我们小飞机EnemyT1 的攻击方式是垂直向下发射子弹。 那么大飞机…...
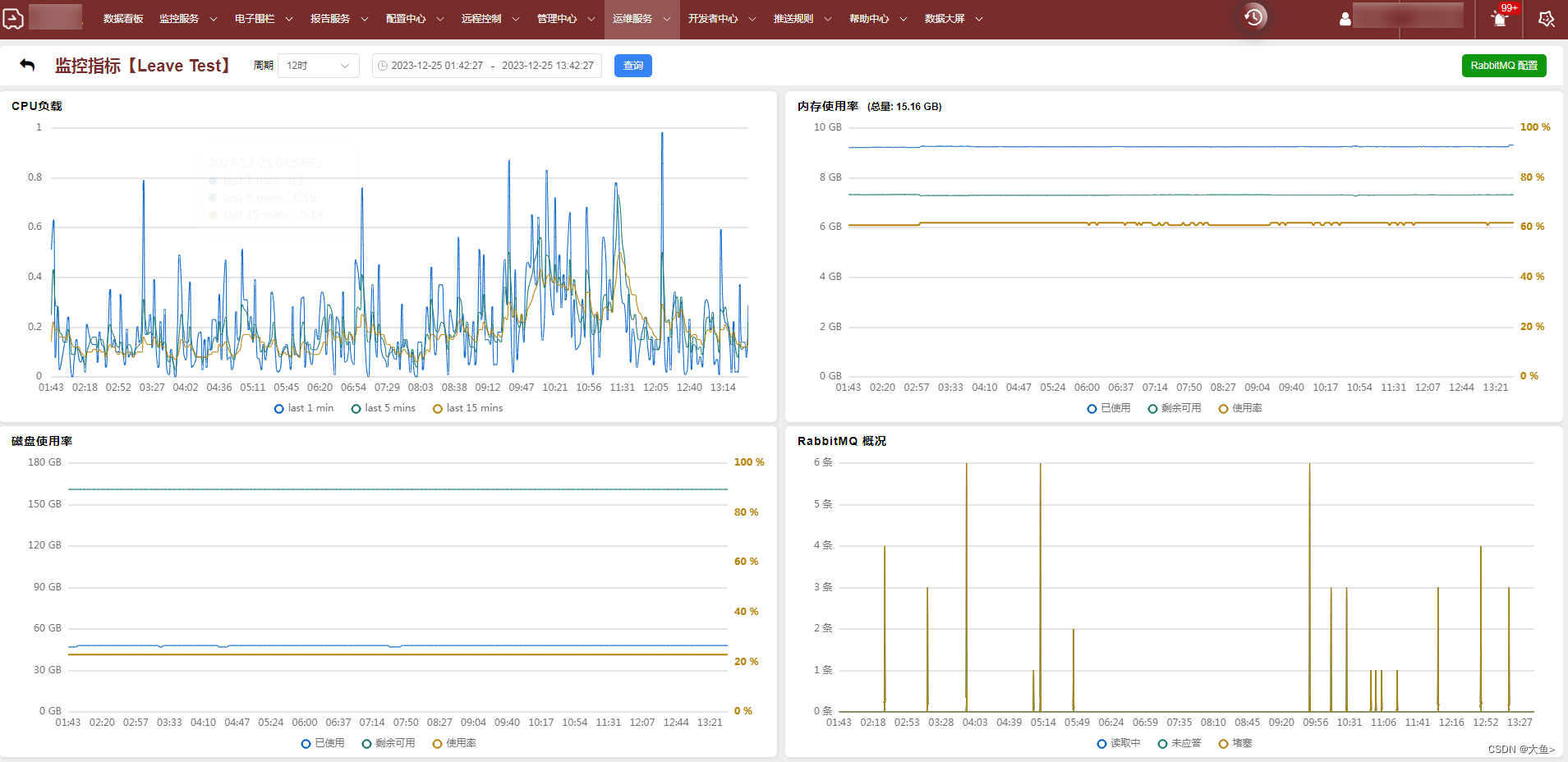
C#获取windows系统资源使用情况
1.前言 之前有一篇博客介绍如何获取Linux服务器上的资源使用情况《Java 获取服务器资源(内存、负载、磁盘容量)》,这里介绍如何通过C#获取Window系统的资源使用。 2.获取服务器资源 2.1.内存 [DllImport("kernel32.dll")][retu…...
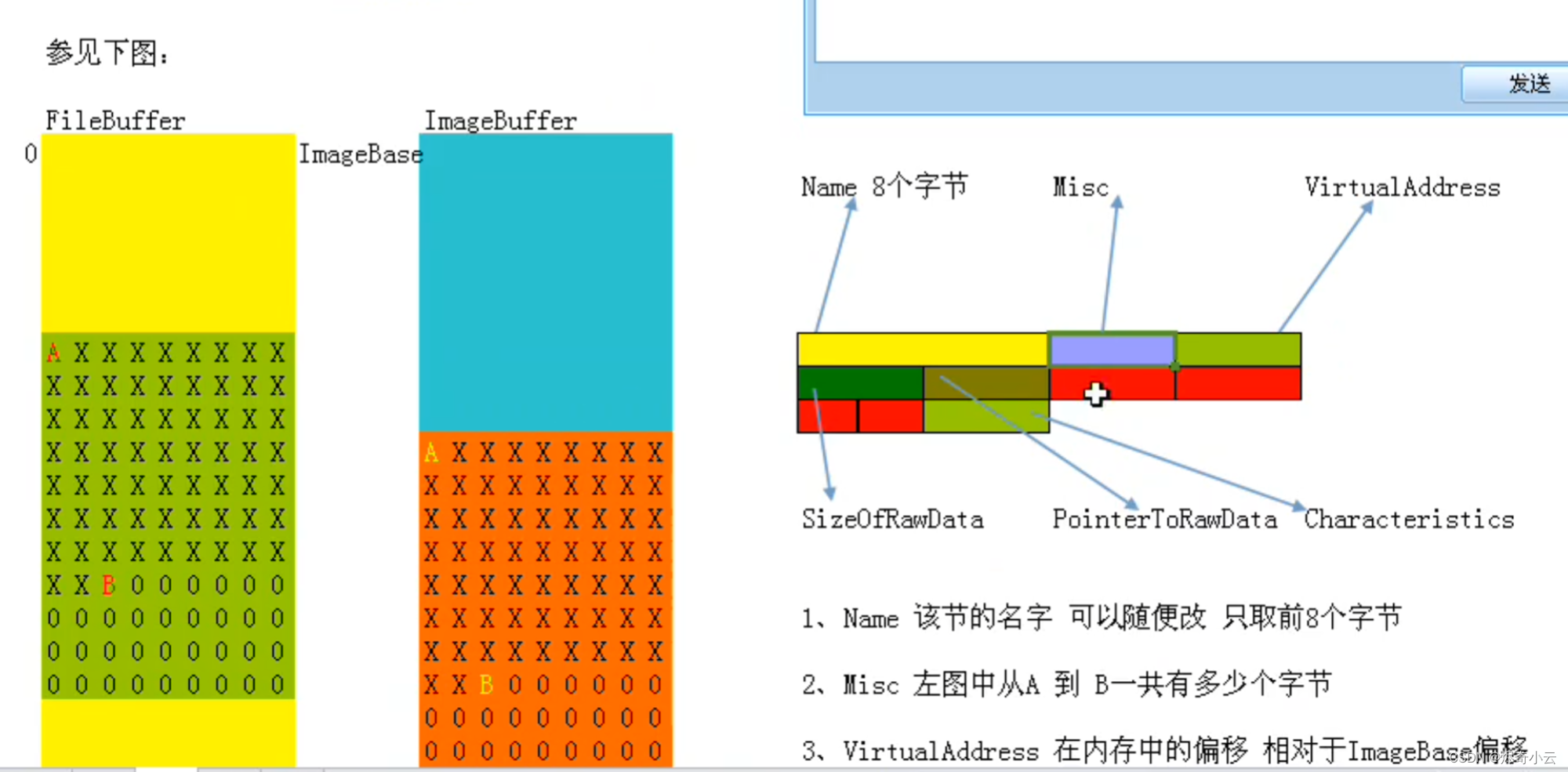
PE解释器之PE文件结构
PE文件是由许许多多的结构体组成的,程序在运行时就会通过这些结构快速定位到PE文件的各种资源,其结构大致如图所示,从上到下依次是Dos头、Nt头、节表、节区和调试信息(可选)。其中Dos头、Nt头和节表在本文中统称为PE文件头(因为SizeOfHeaders…...
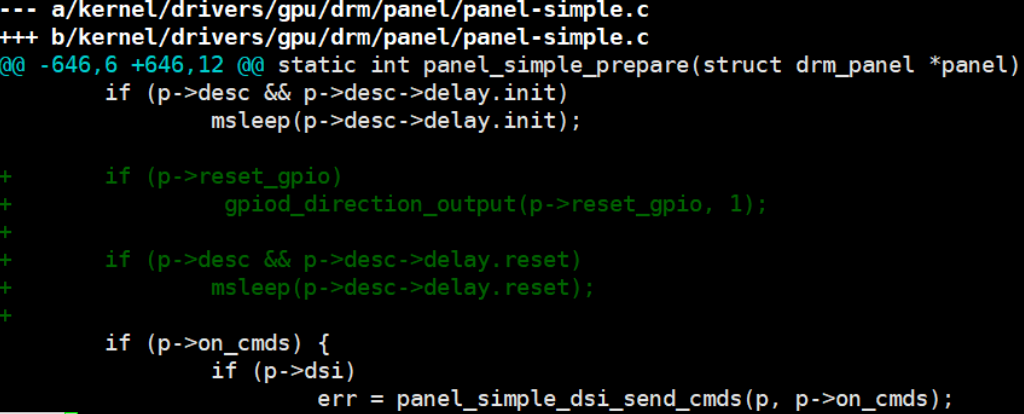
Android—— MIPI屏调试
一、实现步骤 1、在kernel/arch/arm/boot/dts/lcd-box.dtsi文件中打开&dsi0节点,关闭其他显示面板接口(&edp_panel、&lvds_panel) --- a/kernel/arch/arm/boot/dts/lcd-box.dtsib/kernel/arch/arm/boot/dts/lcd-box.dtsi-5,14 …...

BLE协议—协议栈基础
BLE协议—协议栈基础 BLE协议栈基础通用访问配置文件层(Generic Access Profile,GAP)GAP角色设备配置模式和规程安全模式广播和扫描 BLE协议栈基础 蓝牙BLE协议栈包含三部分:主机、主机接口层和控制器。 主机:逻辑链路…...

yolov8知识蒸馏代码详解:支持logit和feature-based蒸馏
文章目录 1. 知识蒸馏理论2. yolov8 蒸馏代码应用2.1 环境配置2.2 训练模型(1) 训练教师模型(2) 训练学生模型baseline(3) 蒸馏训练3. 知识蒸馏代码详解3.1 蒸馏参数设置3.2 蒸馏损失代码讲解3.2.1 Feature based loss3.2.1 Logit loss3.3 获取蒸馏的feature map及channels...
03-微服务-Ribbon负载均衡
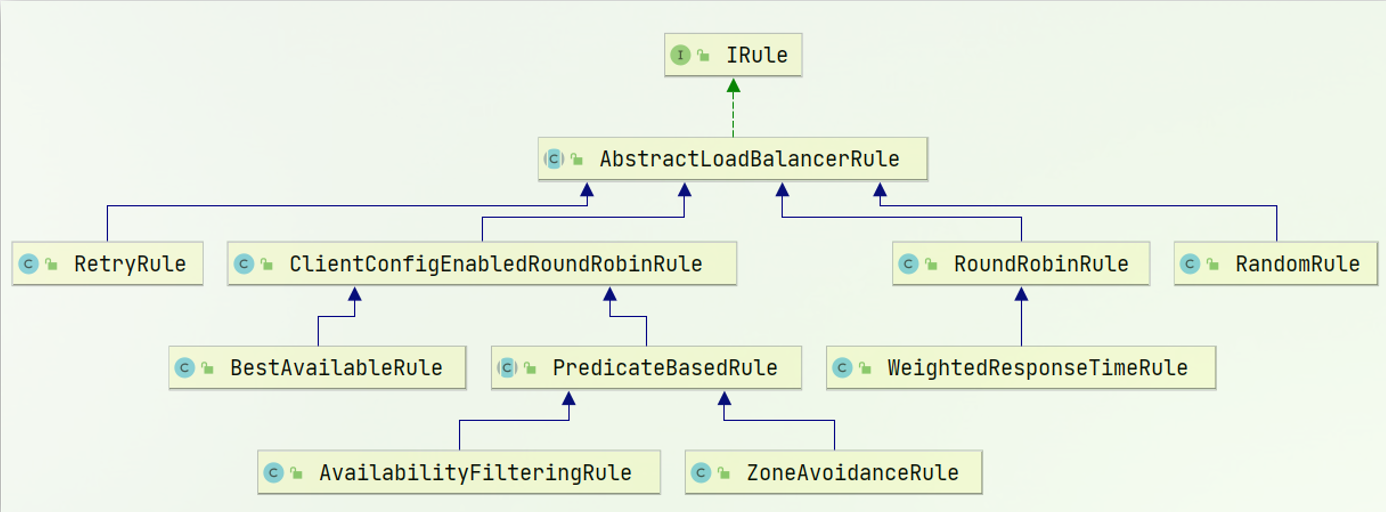
Ribbon负载均衡 1.1.负载均衡原理 SpringCloud底层其实是利用了一个名为Ribbon的组件,来实现负载均衡功能的。 那么我们发出的请求明明是http://userservice/user/1,怎么变成了http://localhost:8081的呢? 1.2.源码跟踪 为什么我们只输入…...

2023新年总结与展望
2023年总结 对Spring Cloud微服务更加熟悉,对consul、kafka、gateway的熟悉和掌握更近一步对docker和虚拟化部署更加熟悉对PostgreSQL数据库和JPA更加熟悉对clickhouse数据库和大数据分析更加熟悉对netty和socket网络通信更加熟悉 2024年flag 继续深入研究和学习…...
论文阅读——SG-Former
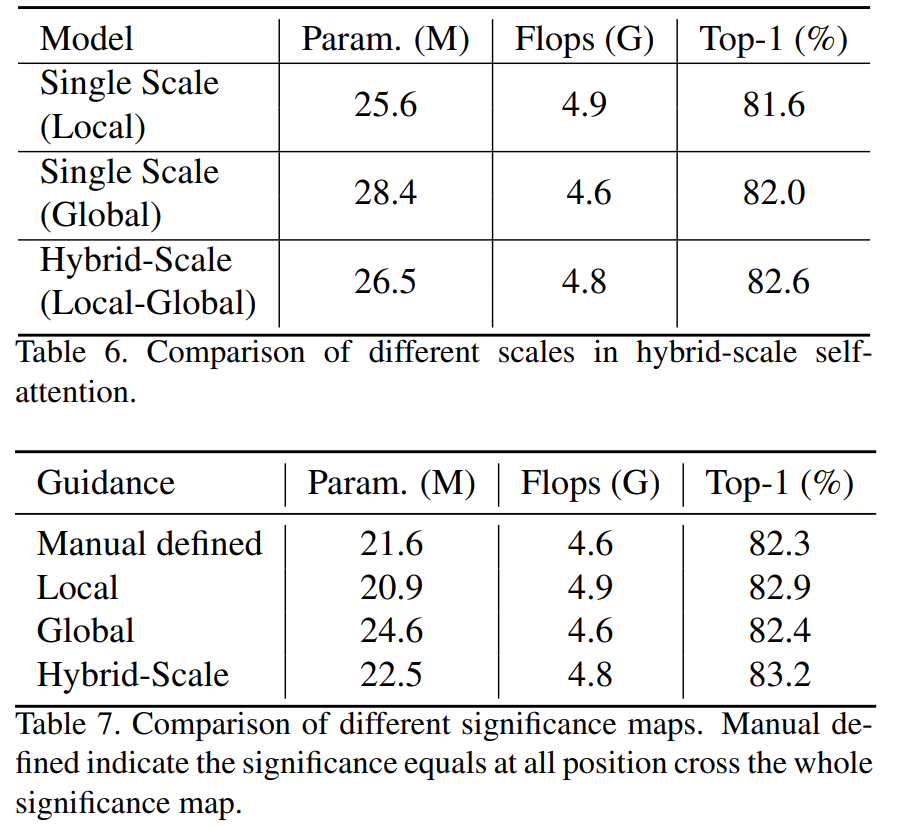
SG-Former: Self-guided Transformer with Evolving Token Reallocation 1. Introduction 方法的核心是利用显著性图,根据每个区域的显著性重新分配tokens。显著性图是通过混合规模的自我关注来估计的,并在训练过程中自我进化。直观地说,我们…...
常用环境部署(十三)——GitLab整体备份及迁移
一、GitLab备份 注意:由于我的GitLab是docker安装的,所以我的操作都是在容器内操作的,大家如果不是用docker安装的则直接执行命令就行。 1、Docker安装GitLab 链接:常用环境部署(八)——Docker安装GitLab-CSDN博客 2、GitLab备…...

海外数据中心代理与住宅代理:优缺点全面对比
数据中心代理和住宅代理是为了匿名而开发的,通过替换网站眼中您自己的 IP 地址。然而,它们在价格、功能、性能或最佳用例方面存在一些差异。那么,这些代理类型到底有什么相似点和不同点呢? 一、什么是数据中心代理? 1…...
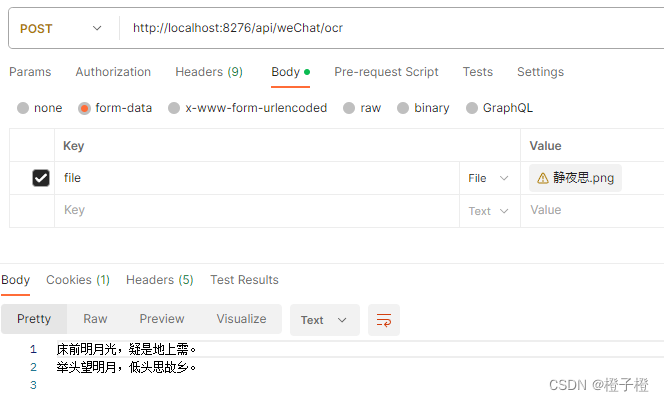
springboot实现OCR
1、引入依赖 <dependency><groupId>net.sourceforge.tess4j</groupId><artifactId>tess4j</artifactId><version>4.5.4</version> </dependency> 2、config Configuration public class TessOcrConfiguration {Beanpublic …...

【Scala 】注解
在 Scala 中,你可以使用注解来为类、方法或字段添加元数据,影响它们的行为。Scala 的注解使用与 Java 类似,但是 Scala 也支持自定义注解。 文章目录 注解的常见使用方法自定义注解 注解的常见使用方法 以下是一些 Scala 中常见的注解以及它…...

数通基础知识总结
1. 基础概念 1.1. 通信基本原理 通信基本原理涉及信息的生成、编码、传输和解码的过程。在实际应用中,例如电话通信,信息通过话筒转换成模拟信号,经过传输线路传递到接收端,再由耳机解码还原为可理解的信息。 1.2. 信道和信号 …...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...

