时间序列平稳性相关检验方法
理解平稳性
一般来说,平稳时间序列是指随着时间的推移具有相当稳定的统计特性的时间序列,特别是在均值和方差方面。平稳性可能是一个比较模糊的概念,将序列排除为不平稳可能比说序列是平稳的更容易。通常不平稳序列有几个特征:
- 平均值随时间推移发生变化,不保持稳定;
- 每个周期的波峰和波谷之间的距离在增长(缩短),也就是序列的方差随时间推移而增加(减小);
- 整个序列表现出强烈的季节性行为,与平稳性相反。
如何判断序列是否平稳?
时间序列平稳性检验方法,一般可分为两类:
- 图形分析方法
- 假设检验方法
1.图形分析方法
这是最简单的方法,即可视化时间序列数据,或可视化时间序列的统计特征,进行肉眼判断。
1.1 可视化数据
import numpy as np
import pandas as pd
import akshare as ak
import matplotlib.pyplot as plt
import seaborn as sns
import warningssns.set(style='darkgrid')
warnings.filterwarnings('ignore')np.random.seed(123)# -------------- 准备数据 --------------
# 白噪声
white_noise = np.random.standard_normal(size=1000)# 随机游走
x = np.random.standard_normal(size=1000)
random_walk = np.cumsum(x)# GDP
df = ak.macro_china_gdp()
df = df.set_index('季度')
# df.index = pd.to_datetime(df.index)
gdp = df['国内生产总值-绝对值'][::-1].astype('float')# GDP DIFF
gdp_diff = gdp.diff(4).dropna()# -------------- 绘制图形 --------------
fig, ax = plt.subplots(2, 2, figsize=(22,16), dpi=300)ax[0][0].plot(white_noise)
ax[0][0].set_title('white_noise')
ax[0][1].plot(random_walk)
ax[0][1].set_title('random_walk')ax[1][0].plot(gdp)
ax[1][0].set_title('gdp')
ax[1][1].plot(gdp_diff)
ax[1][1].set_title('gdp_diff')plt.show()

- 白噪声:曲线围绕0值上下波动,波动幅度前后、上下一致,为平稳序列;
- 随机游走:曲线无确定趋势,均值、方差波动较大,非平稳序列;
- GDP数据趋势上升,均值随时间增加,非平稳序列;
- GDP季节差分后数据,曲线大致在一条水平线上下波动,波动幅度前后变化较小,可认为是平稳的。
1.2 可视化统计特征
可视化统计特征,是指绘制时间序列自相关图和偏自相关图,根据自相关图的表现来判断序列是否平稳。
自相关,也叫序列相关,是一个信号与自身不同时间点的相关度,或者说与自身的延迟拷贝(或滞后性)的相关性,是延迟的函数。不同滞后期得到的自相关系数,叫自相关图。(这里有一个默认假设是序列是平稳序列,平稳序列的自相关性只和时间间隔k有关,不随时间t的变化而变化,因而可以称自相关函数是延迟k的函数)
平稳序列通常具有短期自相关性,对于平稳的时间序列,自相关系数往往会迅速退化到零(滞后期约短相关性越高,滞后期为0,相关性为1);而对于非平稳的数据,退化会发生得更慢,或存在先减后增或者周期性波动等变动。
自相关的计算公式为根据滞后期 k k k将序列拆成等长的两个序列,计算两个序列的相关性得到滞后期为 k k k时的自相关性。举例:
X = [ 2 , 3 , 4 , 3 , 8 , 7 ] , A = [ 2 , 3 , 4 , 3 , 8 ] , B = [ 3 , 4 , 3 , 8 , 7 ] X=[2,3,4,3,8,7],\quad A=[2,3,4,3,8], \quad B=[3,4,3,8,7] X=[2,3,4,3,8,7],A=[2,3,4,3,8],B=[3,4,3,8,7]
X ˉ = 1 6 ∑ i = 1 6 X i = 4.5 \bar{X} = \frac{1}{6} \sum_{i=1}^{6}X_i = 4.5 Xˉ=61i=1∑6Xi=4.5
s 2 ( X ) = 1 6 ∑ i = 1 6 ( X i − X ˉ ) ( X i − X ˉ ) = 4.916 s^2(X)=\frac{1}{6} \sum_{i=1}^{6}(X_i- \bar{X})(X_i- \bar{X})=4.916 s2(X)=61i=1∑6(Xi−Xˉ)(Xi−Xˉ)=4.916
r ( 1 ) = 1 5 ( A i − X ˉ ) ( B i − X ˉ ) = 1.75 r(1)=\frac{1}{5}(A_i-\bar{X})(B_i-\bar{X})=1.75 r(1)=51(Ai−Xˉ)(Bi−Xˉ)=1.75
A C F ( 1 ) = r ( 1 ) s 2 ( X ) = 0.356 ACF(1)=\frac{r(1)}{s^2(X)}=0.356 ACF(1)=s2(X)r(1)=0.356
import statsmodels.api as sm
X = [2,3,4,3,8,7]
sm.tsa.stattools.acf(X, nlags=1, adjusted=True) # 返回值:[滞后期为0时的自相关性,滞后期为1的自相关系数]
array([1. , 0.3559322])
根据 A C F ACF ACF求出滞后 k k k自相关系数时,实际上得到并不是 X ( t ) X(t) X(t)与 X ( t − k ) X(t-k) X(t−k)之间单纯的相关关系。因为 X ( t ) X(t) X(t)还会受到中间 k − 1 k-1 k−1个随机变量的影响,而这 k − 1 k-1 k−1个随机变量又都和 X ( t − k ) X(t-k) X(t−k)具有相关关系,如果提出中间 k − 1 k-1 k−1个随机变量的影响,所计算得到的是偏自相关系数,计算较为复杂。
# 数据生成过程在第一个代码块中
from statsmodels.graphics.tsaplots import plot_acf, plot_pacffig, ax = plt.subplots(4, 2, figsize=(22, 16), dpi=300)
fig.subplots_adjust(hspace=1.2)plot_acf(white_noise, ax=ax[0][0])
ax[0][0].set_title('ACF(white_noise)')
plot_pacf(white_noise, ax=ax[0][1])
ax[0][1].set_title('PACF(white_noise)')plot_acf(random_walk, ax=ax[1][0])
ax[1][0].set_title('ACF(random_walk)')
plot_pacf(random_walk, ax=ax[1][1])
ax[1][1].set_title('PACF(random_walk)')plot_acf(gdp, ax=ax[2][0])
ax[2][0].set_title('ACF(gdp)')
plot_pacf(gdp, ax=ax[2][1])
ax[2][1].set_title('PACF(gdp)')plot_acf(gdp_diff, ax=ax[3][0])
ax[3][0].set_title('ACF(gdp_diff)')
plot_pacf(gdp_diff, ax=ax[3][1])
ax[3][1].set_title('PACF(gdp_diff)')plt.show()

- 白噪音的自相关系数很快就衰减到0附近,是明显的平稳序列。滞后期为0时的自相关系数和偏自相关系数其实就是序列自己和自己的相关性,故为1;滞后期为1时,自相关系数为0,表示白噪声无自相关性;
- 随机游走,自相关系数下降非常缓慢,故为非平稳序列;另从偏自相关系数中可以看到随机游走只和前一项有关;
- GDP数据的自相关图中也可以看到存在一定的周期性,滞后4、8、12等自相关系数较大下降较慢,差分后下降多一些起到一定效果,认为差分后序列是平稳的。同可视化数据一样,直观判断带有较强主观性,但能让我们对数据有更直观的认识。
2.假设检验
平稳性的假设检验方法当前主流为单位根检验,检验序列中是否存在单位根,若存在,则为非平稳序列,不存在则为平稳序列。
2.1 DF检验
A D F ADF ADF检验(Augmented Dickey-Fuller Testing)是最常用的单位根检验方法之一,通过检验序列是否存在单位根来判断序列是否是平稳的。 A D F ADF ADF是 D F DF DF检验的增强版。
迪基(Dickey)和弗勒(Fuller)1979年基于非平稳序列的基本特征将其大致归为三类并提出DF检验:
- 当序列基本走势呈现无规则上升或下降并反复时,将其归为无漂移项自回归过程;
- 当序列基本走势呈现明显的随时间递增或递减且趋势并不太陡峭时,将其归为带漂移项自回归过程;
- 当序列基本走势随时间快速递增时,则将其归为带趋势项回归过程。
对应检验回归式为:
- 无漂移项自回归过程: Y t = ρ Y t − 1 + ε t , Y 0 = 0 Y_t=\rho Y_{t-1} + \varepsilon_t, \quad Y_0=0 Yt=ρYt−1+εt,Y0=0
- 带漂移项自回归过程: Y t = μ + ρ Y t − 1 + ε t , Y 0 = 0 Y_t=\mu + \rho Y_{t-1} + \varepsilon_t, \quad Y_0=0 Yt=μ+ρYt−1+εt,Y0=0
- 带漂移项和趋势项自回归过程: Y t = μ + β t + ρ Y t − 1 + ε t , Y 0 = 0 Y_t=\mu + \beta_t + \rho Y_{t-1} + \varepsilon_t, \quad Y_0=0 Yt=μ+βt+ρYt−1+εt,Y0=0
其中 μ \mu μ是常数项, β t \beta_t βt是趋势项, ε t \varepsilon_t εt为白噪声无自相关性。
- 原假设 H 0 : ρ = 1 H_0: \rho = 1 H0:ρ=1(存在单位根,为非平稳时间序列);
- 备择假设 H 1 : ρ < 1 H_1: \rho < 1 H1:ρ<1(不存在单位根,时间序列是平稳的:不含截距项和趋势项的平稳/含截距项的平稳/含截距项和趋势平稳);
若检验统计量大于临界值( P P P值大于显著性水平 α \alpha α),不能拒绝原假设,序列是非平稳的;
若检验统计量小于临界值( P P P值小于显著性水平 α \alpha α),拒绝原假设,序列是平稳的。
2.2 ADF检验
D F DF DF检验公式为一阶自回归过程,为了能适用于高阶自回归过程的平稳性检验,迪基等1984年对 D F DF DF检验进行了一定的修正,引入了更高阶的滞后项, A D F ADF ADF的检验回归式修正为:
- 无漂移项自回归过程: Y t = ρ Y t − 1 + ∑ i = 1 k C i △ Y t − i + ε t , Y 0 = 0 Y_t=\rho Y_{t-1} + \sum_{i=1}^{k}C_i\bigtriangleup Y_{t-i} + \varepsilon_t, \quad Y_0=0 Yt=ρYt−1+∑i=1kCi△Yt−i+εt,Y0=0
- 带漂移项自回归过程: Y t = μ + ρ Y t − 1 + ∑ i = 1 k C i △ Y t − i + ε t , Y 0 = 0 Y_t=\mu + \rho Y_{t-1} + \sum_{i=1}^{k}C_i\bigtriangleup Y_{t-i} + \varepsilon_t, \quad Y_0=0 Yt=μ+ρYt−1+∑i=1kCi△Yt−i+εt,Y0=0
- 带漂移项和趋势项自回归过程: Y t = μ + β t + ρ Y t − 1 + ∑ i = 1 k C i △ Y t − i + ε t , Y 0 = 0 Y_t=\mu + \beta_t + \rho Y_{t-1} + \sum_{i=1}^{k}C_i\bigtriangleup Y_{t-i} + \varepsilon_t, \quad Y_0=0 Yt=μ+βt+ρYt−1+∑i=1kCi△Yt−i+εt,Y0=0
其中 μ \mu μ是常数项, β t \beta_t βt是趋势项, ε t \varepsilon_t εt为白噪声无自相关性。
假设条件不变:
- 原假设 H 0 : ρ = 1 H_0: \rho = 1 H0:ρ=1(存在单位根,为非平稳时间序列);
- 备择假设 H 1 : ρ < 1 H_1: \rho < 1 H1:ρ<1(不存在单位根,时间序列是平稳的:不含截距项和趋势项的平稳/含截距项的平稳/含截距项和趋势平稳);
检验流程同 D F DF DF检验一致。若要严格判断序列是否是宽平稳的,可以直接检验是否不含截距项和趋势项平稳;若不能拒绝原假设(如 p > 0.05 p>0.05 p>0.05),序列非平稳,此时仍有必要检验序列是否是趋势平稳的。非平稳且非趋势平稳,可以使用一阶差分等平稳化方法处理后再做检验,弱势趋势平稳,困于过度差分则不宜使用差分方式平稳化。
import numpy as np
from matplotlib import pyplot as pltnp.random.seed(123)y = np.random.standard_normal(size=100)
for i in range(1, len(y)):y[i] = 1 + 0.1*i + y[i]plt.figure(figsize=(12, 6), dpi=300)
plt.plot(y)
plt.show()

from arch.unitroot import ADF
adf = ADF(y)
print(adf.summary().as_text())adf = ADF(y, trend='ct')
print(adf.summary().as_text())
Augmented Dickey-Fuller Results
=====================================
Test Statistic -0.739
P-value 0.836
Lags 5
-------------------------------------Trend: Constant
Critical Values: -3.50 (1%), -2.89 (5%), -2.58 (10%)
Null Hypothesis: The process contains a unit root.
Alternative Hypothesis: The process is weakly stationary.Augmented Dickey-Fuller Results
=====================================
Test Statistic -9.963
P-value 0.000
Lags 0
-------------------------------------Trend: Constant and Linear Time Trend
Critical Values: -4.05 (1%), -3.46 (5%), -3.15 (10%)
Null Hypothesis: The process contains a unit root.
Alternative Hypothesis: The process is weakly stationary.
arch包中 A D F ADF ADF检验可指定trend = "n"(不含截距项和时间趋势项)、trend = "c"(含截距项)、trend = "ct"(含截距项和时间趋势项)、trend = "ctt"(含截距项、时间趋势项和二次型时间趋势项),分别对应不同平稳类型的检验。
再来看看GDP季节差分前后数据是否为平稳:
# 数据在第一个代码块中
from arch.unitroot import ADF
adf = ADF(gdp)
print(adf.summary().as_text())adf = ADF(gdp_diff) # 差分后平稳
print(adf.summary().as_text())
Augmented Dickey-Fuller Results
=====================================
Test Statistic 2.606
P-value 0.999
Lags 12
-------------------------------------Trend: Constant
Critical Values: -3.55 (1%), -2.91 (5%), -2.59 (10%)
Null Hypothesis: The process contains a unit root.
Alternative Hypothesis: The process is weakly stationary.Augmented Dickey-Fuller Results
=====================================
Test Statistic -3.651
P-value 0.005
Lags 8
-------------------------------------Trend: Constant
Critical Values: -3.55 (1%), -2.91 (5%), -2.59 (10%)
Null Hypothesis: The process contains a unit root.
Alternative Hypothesis: The process is weakly stationary.
# 数据在第一个代码块中
from arch.unitroot import ADF
adf = ADF(gdp, trend='ct') # 差分前非趋势平稳
print(adf.summary().as_text())
Augmented Dickey-Fuller Results
=====================================
Test Statistic -2.358
P-value 0.402
Lags 4
-------------------------------------Trend: Constant and Linear Time Trend
Critical Values: -4.10 (1%), -3.48 (5%), -3.17 (10%)
Null Hypothesis: The process contains a unit root.
Alternative Hypothesis: The process is weakly stationary.
2.3 PP检验
Phillips和Perron(1988)提出了一种非参数检验方法,主要是为了解决残差项中潜在的序列相关和异方差问题,其检验统计量的渐进分布和临界值与ADF检验相同。同样出现较早,假设条件一样,用法相似,可作为ADF检验的补充。
假设条件不变:
- 原假设 H 0 : ρ = 1 H_0: \rho = 1 H0:ρ=1(存在单位根,为非平稳时间序列);
- 备择假设 H 1 : ρ < 1 H_1: \rho < 1 H1:ρ<1(不存在单位根,时间序列是平稳的:不含截距项和趋势项的平稳/含截距项的平稳/含截距项和趋势平稳);
同样构造一个趋势平稳序列,看下PP检验结果:
import numpy as np
from arch.unitroot import PhillipsPerronnp.random.seed(123)y = np.random.standard_normal(size=100)
for i in range(1, len(y)):y[i] = 1 + 0.1*i + y[i]pp = PhillipsPerron(y) # 10%显著水平下平稳
print(pp.summary().as_text())pp = PhillipsPerron(y, trend='ct') # 1%显著水平下趋势平稳
print(pp.summary().as_text())
Phillips-Perron Test (Z-tau)
=====================================
Test Statistic -2.825
P-value 0.055
Lags 12
-------------------------------------Trend: Constant
Critical Values: -3.50 (1%), -2.89 (5%), -2.58 (10%)
Null Hypothesis: The process contains a unit root.
Alternative Hypothesis: The process is weakly stationary.Phillips-Perron Test (Z-tau)
=====================================
Test Statistic -10.009
P-value 0.000
Lags 12
-------------------------------------Trend: Constant and Linear Time Trend
Critical Values: -4.05 (1%), -3.46 (5%), -3.15 (10%)
Null Hypothesis: The process contains a unit root.
Alternative Hypothesis: The process is weakly stationary.
2.4 DF-GLS检验
DF-GLS检验,是Elliot,Rothenberg,and Stock 1996年提出的一种单位根检验方法,全称Dickey-Fuller Test with GLS Detredding,即“使用广义最小二乘法去除趋势的检验”,是目前最有功效的单位根检验。
DF-GLS检验利用广义最小二乘法,首先对要检验的数据进行一次“准差分”,然后利用准差分的数据对原序列进行去除趋势处理,再利用ADF检验的模型形式对去除趋势后的数据进行单位根检验,但此时ADF检验模型中不再包含常数项或者时间趋势变量。
- 原假设:序列存在单位根(时间序列是非平稳的);
- 备择假设:序列不存在单位根(时间序列是平稳的或趋势平稳的)
同样构造一个趋势平稳序列来看下检验效果(DF-GLS检验trend只能指定为c或ct):
import numpy as np
from arch.unitroot import DFGLSnp.random.seed(123)y = np.random.standard_normal(size=100)
for i in range(1, len(y)):y[i] = 1 + 0.1*i + y[i]dfgls = DFGLS(y)
print(dfgls.summary().as_text())dfgls = DFGLS(y, trend='ct') # 趋势平稳
print(dfgls.summary().as_text())
Dickey-Fuller GLS Results
=====================================
Test Statistic 1.186
P-value 0.945
Lags 4
-------------------------------------Trend: Constant
Critical Values: -2.77 (1%), -2.15 (5%), -1.83 (10%)
Null Hypothesis: The process contains a unit root.
Alternative Hypothesis: The process is weakly stationary.Dickey-Fuller GLS Results
=====================================
Test Statistic -7.565
P-value 0.000
Lags 0
-------------------------------------Trend: Constant and Linear Time Trend
Critical Values: -3.62 (1%), -3.04 (5%), -2.74 (10%)
Null Hypothesis: The process contains a unit root.
Alternative Hypothesis: The process is weakly stationary.
2.5 KPSS检验
KPSS检验是由Kwiatkowski, Phillips, and Shin 1992年提出的,与之前的检验方法相比,最大的不同点就是它的原假设是平稳序列或趋势平稳序列,而备择假设是存在单位根。
- 原假设:序列不存在单位根(时间序列是平稳的或趋势平稳的)
- 备择假设:序列存在单位根(时间序列是非平稳的)
import numpy as np
from arch.unitroot import KPSSnp.random.seed(123)y = np.random.standard_normal(size=100)
for i in range(1, len(y)):y[i] = 0.1 + y[i-1] + y[i]kpss = KPSS(y)
print(kpss.summary().as_text())kpss = KPSS(y, trend='ct')
print(kpss.summary().as_text())
KPSS Stationarity Test Results
=====================================
Test Statistic 1.393
P-value 0.000
Lags 5
-------------------------------------Trend: Constant
Critical Values: 0.74 (1%), 0.46 (5%), 0.35 (10%)
Null Hypothesis: The process is weakly stationary.
Alternative Hypothesis: The process contains a unit root.KPSS Stationarity Test Results
=====================================
Test Statistic 0.114
P-value 0.115
Lags 5
-------------------------------------Trend: Constant and Linear Time Trend
Critical Values: 0.22 (1%), 0.15 (5%), 0.12 (10%)
Null Hypothesis: The process is weakly stationary.
Alternative Hypothesis: The process contains a unit root.
KPSS检验中原假设为不存在单位根。默认检验趋势类型下P值为0.000,拒绝原假设,存在单位根,序列非平稳。指定trend="ct"后,P值不拒绝原假设,认为序列趋势平稳,检验错误。以上几种检验均不能100%保证检验正确,PP检验可认为是ADF检验的补充,KPSS检验同样也可和其他检验一同使用,当均认为是平稳或趋势平稳时方判定为平稳。
相关文章:

时间序列平稳性相关检验方法
理解平稳性 一般来说,平稳时间序列是指随着时间的推移具有相当稳定的统计特性的时间序列,特别是在均值和方差方面。平稳性可能是一个比较模糊的概念,将序列排除为不平稳可能比说序列是平稳的更容易。通常不平稳序列有几个特征: …...

<leetcode修炼>双指针训练-移动零
题目: 给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。 请注意 ,必须在不复制数组的情况下原地对数组进行操作。 方法1: 快慢指针 快指针负责遍历数组中所有元素,慢指针负责记录不为0的…...
Python初探:从零开始的编程奇妙之旅
一、Python是什么 Python是一门多用途的高级编程语言,以其简洁、易读的语法而脱颖而出。在深度学习领域,Python扮演着至关重要的角色。其丰富的科学计算库(如NumPy、Pandas、Matplotlib)和强大的深度学习框架(如Tenso…...
算法与数据结构之链表<一>(Java)
目录 1、链表的定义 2、链表的特点 3、为何要使用链表 4、数组与链表的区别 5、链表的增删查 5.1、在头部插入链表 5.2、在中间插入链表 5.3、删除头节点 5.4、删除中间节点 5.5、查询某个值 6、链表的应用 6.1 如何设计一个LRU缓存算法? 6.2 约瑟夫问题 1、链表的定…...
目标检测COCO数据集与评价体系mAP
1.mAP 2.IoU IoU也就是交并比,也称为 Jaccard 指数,用于计算真实边界框与预测边界框之间的重叠程度。它是真值框与预测边界框的交集和并集之间的比值。Ground Truth边界框是测试集中手工标记的边界框,用于指定对象图像的位置以及预测的边界框…...

2024最全面且有知识深度的web3开发工具、web3学习项目资源平台
在Web3技术迅速发展的时代,寻找一个综合且深入的Web3开发工具和学习项目资源平台变得至关重要。今天,我将向大家介绍一个非常有价值的网站,它就是https://web3x.world 。 Web3X是一个全面而深入的Web3开发者社区,为开发者们提供了…...

Golang - defer关键字 深入剖析
defer关键字 defer和go一样都是Go语言提供的关键字。defer用于资源的释放,会在函数返回之前进行调用。一般采用如下模式: f,err : os.Open(filename) if err ! nil {panic(err) } defer f.Close()如果有多个defer表达式,调用顺序类似于栈&a…...

如何在Spring Boot中使用@Scheduled写定时任务判断数据量是否过大,过大则进行分表操作,多张表使用临时视图查询
当数据量过大,在定时任务中执行分表操作 1、复制表结构及数据 在xml中编写复制表结构及数据(newTableName为新表名、originalTableName为原始表名) 只复制表结构: CREATE TABLE ${newTableName} AS SELECT * FROM ${originalTa…...

使用jieba库进行中文分词和去除停用词
jieba.lcut jieba.lcut()和jieba.lcut_for_search()是jieba库中的两个分词函数,它们的功能和参数略有不同。 jieba.lcut()方法接受三个参数:需要分词的字符串,是否使用全模式(默认为False)以及是否使用HMM模型&…...
C语言之分支与循环【附6个练习】
文章目录 前言一、什么是语句?1.1 表达式语句1.2 函数调用语句1.3 控制语句1.4 复合语句1.5 空语句 二、分支语句(选择结构)2.1 if语句2.1.1 悬空else2.1.2 练习(1. 判断一个数是否为奇数 2. 输出1-100之间的奇数) 2.2…...
使用通用MCU实现无人机飞行任务的快速二次开发
使用通用MCU实现无人机飞行任务的快速二次开发 ---TIDronePilot外部控制offboard模式介绍 无名小哥 2024年1月1日 传统飞控二次开发方法和主要存在的问题简介 通过对前面几讲中《零基础竞赛无人机积木式编程指南》系列开发教程的学习可知,在以往TI电赛真题的学习…...

什么是Selinux
官网地址:What is SELinux? 欢迎关注留言,我是收集整理小能手,工具翻译,仅供参考,笔芯笔芯. 概述 安全增强型 Linux (SELinux) 是Linux 系统的安全架构,允许管理员更好地控制谁可以访问系统。它最初是由美…...

计算机网络知识点
1. URI 和 URL 统一资源定位符(Uniform Resource Locator,缩写:URL),是对资源的引用和访问该资源的方法。俗称网址,就是浏览器地址栏里面的内容。 URL 语法为:protocol://userInfohost:port/p…...

Qt 连接 Mysql
Linux下安装mysql及qt连接_liunx下安装mysql及qt链接-CSDN博客...
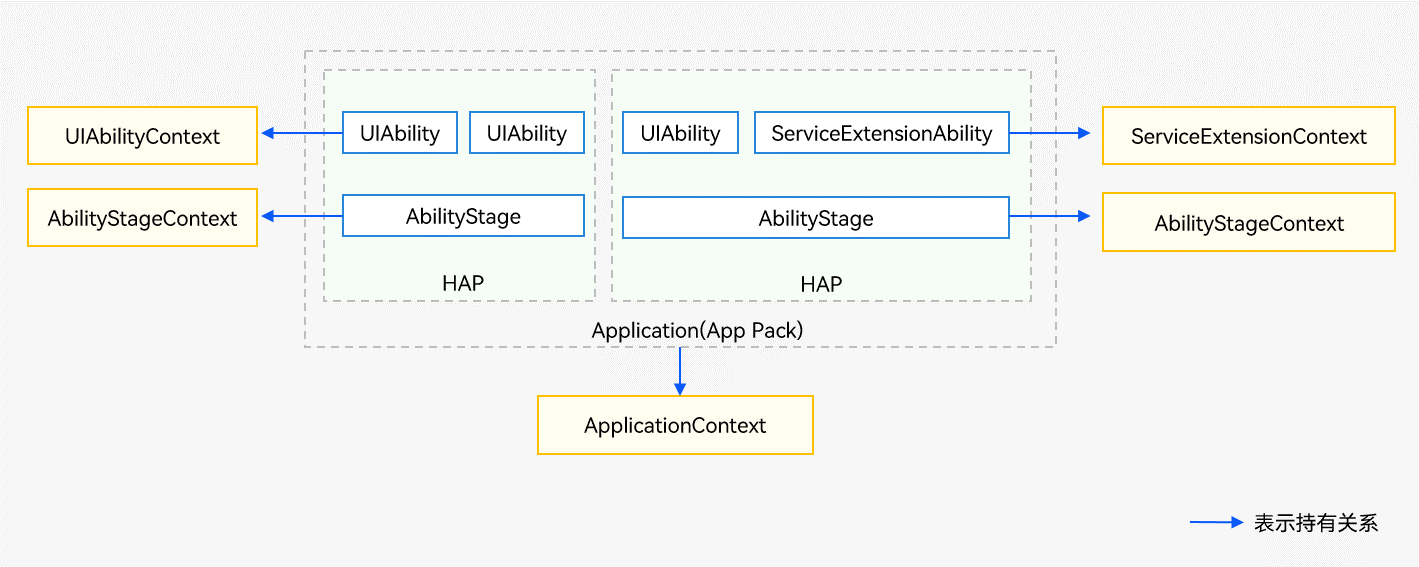
HarmonyOS4.0系统性深入开发14AbilityStage组件容器
AbilityStage组件容器 AbilityStage是一个Module级别的组件容器,应用的HAP在首次加载时会创建一个AbilityStage实例,可以对该Module进行初始化等操作。 AbilityStage与Module一一对应,即一个Module拥有一个AbilityStage。 DevEco Studio默…...
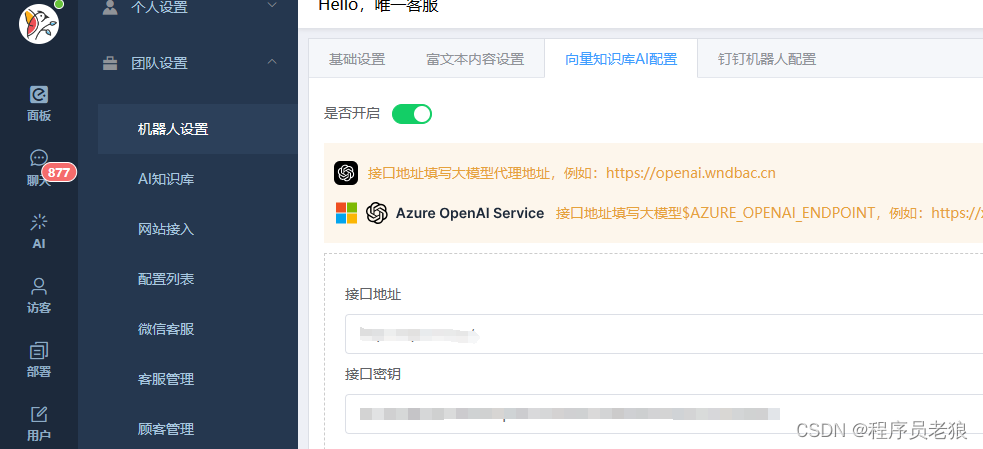
客服系统接入FastGPT
接入FastGPT 点击【应用】【外部使用】【API访问】【新建】新建一个KEY,同时也可以看到我们的API根地址 这个根地址和Key可以填入任何支持OpenAI接口的应用里,这个接口是兼容OpenAI格式。 在客服系统【知识库AI配置】里填上接口地址和接口密钥。这样我…...

Hi5 2.0 虚拟手与追踪器(Tracker)的位置修正
问题描述 使用环境与工具:Unity 2022.3.4fc1,steam VR(2.7.3),steamvrSDK(1.14.15),HTC vive pro专业版,Hi5 2.0数据手套 首先按照Hi5 2.0的使用说明(可参考:HI5 2.0 交…...
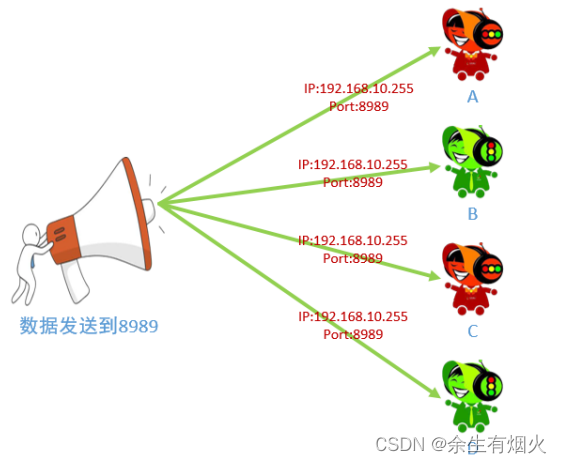
广播及代码实现
广播(Broadcast)是一种网络通信方式,它允许一台设备向网络中的所有其他设备发送消息。广播通常用于在网络上传递一些信息,让所有设备都能接收并处理。在广播中,通信的目标是整个网络而不是特定的单个设备。 向子网中…...

QT应用篇 三、QML自定义显示SpinBox的加减按键图片及显示值效果
QT应用篇 一、QT上位机串口编程 二、QML用Image组件实现Progress Bar 的效果 三、QML自定义显示SpinBox的加减按键图片及显示值效果 文章目录 QT应用篇前言一、qml需求二、使用组件1.SpinBox组件2.SpinBox中QML的使用 总结 前言 记录自己学习QML的一些小技巧方便日后查找 QT的…...

2022年全国职业院校技能大赛网络安全竞赛试题1-10-B模块总结
前言 结尾有对22年国赛题型总结 试题1模块B 网络安全事件响应、数字取证调查和应用安全 B-1任务一:主机发现与信息收集 *任务说明:仅能获取Server1的IP地址 1.通过渗透机Kali2.0对靶机场景进行TCP同步扫描 (使用Nmap工具),并将该操作使用…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...
