网络流总结
网络流总结
- 基础知识
- 最大流最小割定理
- 最大流
- EK
- dinic
- 模型
- 二分图匹配
- 无源汇上下界可行流
- 有源汇上下界最大、最小流
- 多源汇最大流
- 最大流之关键边
- 最大流之拆点
- 最大流建图实战
- 最小割
- 模型
- 最大权闭合子图
- 最大密度子图
- 最小点权覆盖集
- 最大点权独立集
- 最小割建图实战
- 费用流
- EK
- 模型
- 费用流与上下界最大流结合
- 费用流建图实战
- 最小割树
基础知识
\qquad 流网络是一个有源点 s s s 和汇点 t t t 的有向图(不考虑反向边),记为 G = ( V , E ) G=(V,E) G=(V,E)。其中每一条边都有一个容量 c ( u , v ) c(u,v) c(u,v) 和一个流量 f ( u , v ) f(u,v) f(u,v)。对于该网络中的一个流 f f f,如果其满足两个条件:1、容量限制,即每条边都满足 0 ≤ f ( u , v ) ≤ c ( u , v ) 0\leq f(u,v)\leq c(u,v) 0≤f(u,v)≤c(u,v);2、流量守恒,即除去源点汇点以外,每个点 x x x 都满足 ∑ u ∈ V f ( u , x ) = ∑ v ∈ V f ( x , v ) \sum_{u\in V}f(u,x)=\sum_{v\in V}f(x,v) ∑u∈Vf(u,x)=∑v∈Vf(x,v),那么我们称流 f f f 是流网络 G G G 的一个可行流。可行流的流量 ∣ f ∣ = ∑ u ∈ V f ( s , u ) − ∑ v ∈ V f ( v , s ) |f|=\sum_{u\in V}f(s,u)-\sum_{v\in V}f(v,s) ∣f∣=∑u∈Vf(s,u)−∑v∈Vf(v,s),即从源点流出的流量减去流入源点的流量。
\qquad 残留网络是针对于原图中的一个流来说的。即,我们只能说“流 f f f 的残留网络 G f G_f Gf”。残留网络对于原图中的每一条边都增加一条反向边,这条反向边的流量与原图中边的流量相等。可以将残留网络中的边理解为“退流”。
\qquad 两个可行流是可以相加减的,叠加的方式就是每条边上的流量对应相加减,而且得到的结果也一定是原图的一个可行流。
\qquad 如果一个流网络中存在一条路径,这条路径中的任意一条边都没有达到满流(即 f ( u , v ) < c ( u , v ) f(u,v)<c(u,v) f(u,v)<c(u,v)),那么我们称这条路径为一条增广路径。
\qquad 流网络中的最大流指的是最大可行流,即第一要满足此流是一条可行流,其次要满足它的流量是本图所有可行流中最大的一个。
\qquad 流网络中的割指的是将图中的所有点分为 S , T S,T S,T 两个点集,记作 C ( S , T ) C(S,T) C(S,T)。这两个点集要满足:1、 s ∈ S , t ∈ T s\in S,t\in T s∈S,t∈T;2、 S ∩ T = ∅ S\cap T=\emptyset S∩T=∅;3、 S ∪ T = V S\cup T=V S∪T=V。割的容量定义为: ∑ u ∈ S , v ∈ T c ( u , v ) \sum_{u\in S,v\in T}c(u,v) ∑u∈S,v∈Tc(u,v),割的流量定义为: ∑ u ∈ S , v ∈ T f ( u , v ) − ∑ u ∈ T , v ∈ S f ( u , v ) \sum_{u\in S,v\in T}f(u,v)-\sum_{u\in T,v\in S}f(u,v) ∑u∈S,v∈Tf(u,v)−∑u∈T,v∈Sf(u,v)。流网络中的最小割指的是容量最小。
最大流最小割定理
\qquad 最大流最小割定理包含三条内容,这三条内容知一推二,分别是:1、可行流 f f f 是最大流;2、可行流 f f f 的残留网络中不存在增广路;3、存在某个割 C ( S , T ) C(S,T) C(S,T),满足 ∣ f ∣ = C ( S , T ) |f| = C(S,T) ∣f∣=C(S,T)。
最大流
\qquad 求最大流有两种算法: E K EK EK 和 d i n i c dinic dinic。
EK
\qquad 根据最大流最小割定理,我们可以得知,当残留网络中不存在增广路时,该残留网络对应的流 f f f 一定是最大流。 E K EK EK 算法便是基于这个原理,每次 b f s bfs bfs 找残留网络中的增广路并将其增广,直到网络中不存在增广路为止。
\qquad E K EK EK 算法时间复杂度为 O ( n m 2 ) O(nm^2) O(nm2),不过网络流算法记时间复杂度用处不大。思路很简单,实现也很容易。
const int maxn = 110;
const int maxm = 5010;
typedef long long LL;
int n, m, S, T;
struct pic {int to, lst;LL cap;
}edge[maxm << 1];
int head[maxn], tot = -1/*边从0开始编号,目的是方便成对变换*/, pre[maxn]/*记录每个点第一次被搜到的前驱边是哪一条*/;
queue < int > q;
LL d[maxn];//记录到达当前点时当前增广路径的最大流量inline void add(int x, int y, int z) {edge[++ tot] = {y, head[x], 1LL * z};head[x] = tot;
}bool bfs() {//寻找增广路memset(vis, 0, sizeof vis);while(!q.empty()) q.pop();q.push(S), vis[S] = 1, d[S] = 1e9 + 7;while(!q.empty()) {int x = q.front(); q.pop();for(int i = head[x]; ~i; i = edge[i].lst) {int y = edge[i].to;if(!vis[y] && edge[i].cap/*有流量时才有意义去搜*/) {d[y] = min(d[x], edge[i].cap);//更新最大流量vis[y] = 1, pre[y] = i;if(y == T) return 1;//找到了一条增广路q.push(y);}}}return 0;
}LL EK() {LL ans = 0;while(bfs()) {ans += d[T];for(int x = T; x != S; x = edge[pre[x] ^ 1/*成对变换*/].to) edge[pre[x]].cap -= d[T], edge[pre[x] ^ 1].cap += d[T];//对增广路进行增广操作}return ans;
}
//main中
memset(head, -1, sizeof head);
scanf("%d%d%d%d", &n, &m, &S, &T);
for(int i = 1, x, y, z; i <= m; i ++) {scanf("%d%d%d", &x, &y, &z);add(x, y, z), add(y, x, 0)/*建残留网络,一开始流量都是0*/;
}
printf("%lld\n", EK());
}
dinic
\qquad 在 E K EK EK 的基础之上,我们考虑优化。
\qquad E K EK EK 每次 b f s bfs bfs 只找出来了一条增广路进行增广,效率较低。 d i n i c dinic dinic 算法依据分层思想,每次找出多条增广路同时进行增广,而且还有三处小优化,总体时间复杂度 O ( n 2 m ) O(n^2m) O(n2m),不过法律规定网络流不许卡 dinic。
bool bfs() {//找增广路memset(d, -1, sizeof d);//分层while(!q.empty()) q.pop();d[1] = 0/*源点层数为0*/, q.push(1), cur[1] = head[1];//当前弧优化while(!q.empty()) {int x = q.front(); q.pop();for(int i = head[x]; ~i; i = edge[i].lst) {int v = edge[i].to; LL w = edge[i].cap;if(d[v] == -1 && w) {d[v] = d[x] + 1/*记录点v在点x下一层*/, cur[v] = head[v];//记录从哪一条边开始跑if(v == n) return 1;q.push(v);}}}return 0;
}LL Find(int x, LL limit) {//limit:当前增广路径的最大流量if(x == n) return limit;//到了汇点LL flow = 0;//增广了多少流量for(int i = cur[x]; ~i && flow < limit/*优化1(最重要):当flow>limit,再搜下去就无意义了,因为无法继续增广了*/; i = edge[i].lst) {cur[x] = i;//优化2:当前弧优化int v = edge[i].to; LL w = edge[i].cap;if(d[v] == d[x] + 1/*判断点v是否是点x的下一层*/ && w) {LL t = Find(v, min(w, limit - flow));if(!t) d[v] = -1;//优化3:如果这个点往后的流量是0,说明通过此点无法进行增广,直接删除即可edge[i].cap -= t, edge[i ^ 1].cap += t, flow += t;}}return flow;
}LL dinic() {LL flow = 0, ans = 0;while(bfs()) while(flow = Find(1, INF)) ans += flow;return ans;
}
模型
二分图匹配
\qquad 例题:飞行员配对方案问题,圆桌问题。
\qquad 套路:用最大流中边的容量来对边进行限制。
无源汇上下界可行流
\qquad 问题:给定一个包含 n n n 个点 m m m 条边的有向图,每条边都有一个流量下界和流量上界。求一种可行方案使得在所有点满足流量平衡条件的前提下,所有边满足流量限制。
\qquad 对于上下界的限制,形式化写出来是: c l o w ( u , v ) ≤ f ( u , v ) ≤ c u p ( u , v ) c_{low}(u,v)\leq f(u,v)\leq c_{up}(u,v) clow(u,v)≤f(u,v)≤cup(u,v),我们可以选择让不等式同时减去 c l o w ( u , v ) c_{low}(u,v) clow(u,v) 从而变成只有上界的问题。但是减完之后可能会有点不满足流量守恒,此时我们需要建立超级源点、超级汇点,根据每个点是少流还是多流来对它们进行补偿或减少(即与源点连还是与汇点连)。而且为了保证这些点一定流量守恒,与源点、汇点相连的边必须要是满流的。所以我们连好与超级源点、汇点的边后,直接在新网络上跑最大流,如果跑出来的不是满流,那么原问题一定无解;否则,让新网络中每条边的流量加上原来的下界,就是原问题的一个可行流。
\qquad 核心 C o d e Code Code:
for(int i = 1, a, b, c, d; i <= m; i ++) {scanf("%d%d%d%d", &a, &b, &c, &d);add(a, b, d - c/*减去下节*/, c/*同时储存下界*/), add(b, a, 0, 0);A[a] -= c, A[b] += c;//记录每条边减去下界后,每个点流量的变化
}
int all = 0;
for(int i = 1; i <= n; i ++) {if(A[i] > 0) add(S, i, A[i], 0), add(i, S, 0, 0), all += A[i];//少流了,需要补else if(A[i] < 0) add(i, T, -A[i], 0), add(T, i, 0, 0);//多留了,需要放
}
if(dinic() < all) puts("NO");//不满流,无解
else {puts("YES");for(int i = 1; i <= (m << 1); i += 2) printf("%d\n", edge[i].cap + edge[i ^ 1].lower);//加上下界
}
有源汇上下界最大、最小流
\qquad 面对上下界,我们可以考虑建一条从汇点指向源点,容量为 I N F INF INF 的边,这样就转化为了无源汇上下界问题。我们可以先沿用无源汇上下界可行流的算法跑出一个可行流,然后将新添的边删去,再从源点向汇点跑出一个最大流,将这两个流相加便是答案。证明我也不太会……
\qquad 核心 C o d e Code Code:
for(int i = 1, a, b, c, d; i <= m; i ++) {scanf("%d%d%d%d", &a, &b, &c, &d);add(a, b, d - c), add(b, a, 0);A[a] -= c, A[b] += c;
}
int all = 0;
for(int i = 1; i <= n; i ++) {if(A[i] > 0) add(S, i, A[i]), add(i, S, 0), all += A[i];else if(A[i] < 0) add(i, T, -A[i]), add(T, i, 0);
}
add(t, s, INF), add(s, t, 0);//添加一条t->s,INF的边
if(dinic() < all) puts("No Solution");
else {int res = edge[tot].cap;//跑出来的可行流,注意不是dinic返回的流,因为dinic返回的是S到T的,我们需要的是s到t的edge[tot].cap = edge[tot ^ 1].cap = 0, S = s, T = t;printf("%d\n", res + dinic());
}
\qquad 对于最小流,我们让上述代码输出 r e s − d i n i c ( ) res-dinic() res−dinic() 即可。证明我还是不会……
多源汇最大流
\qquad 超级源点指向各个源点,各个汇点指向超级汇点,然后跑最大流即可。
最大流之关键边
\qquad 问题:如果升高一条边的容量可以使得最大流变大,那么我们称这条边为“关键边”。现在求网络中有几条“关键边”。
\qquad 我们思考,什么样的边可以成为关键边?
\qquad 在跑完最大流后,如果存在一条路径,这条路径中只有一条边是满流的,那么这条边一定是关键边。证明也很显然。那么,我们只需跑完最大流后,分别从源点和汇点开始 d f s dfs dfs,每次只走没满流的边。搜完之后,如果一条边的两端点分别被源点和汇点搜到,那么它一定是关键边。
最大流之拆点
\qquad 当我们有时要对点进行限制时,我们可以考虑拆点,在拆出的点之间加边来满足对点的限制。
\qquad 例题:[USACO07OPEN] Dining G,最长不下降子序列问题。
最大流建图实战
\qquad 例题:MPIGS - Sell Pigs,[SCOI2007] 蜥蜴,清理雪道。
最小割
\qquad 根据“最大流最小割定理”,我们可以得知,网络中最小割的容量就是最大流的流量,所以我们完全可以用求最大流的方法求最小割。
\qquad 但是,如果让求最小割的方案,怎么办呢?
\qquad 参考最大流求关键边的做法,我们可以从源点开始 d f s dfs dfs,每次只走没满流的边。最后如果有一条边的两个端点有一个被搜到了,另一个没有,那么这条边就要被割开。这也就意味着,整个图可以被分为“被搜到的点”和“没被搜到的点”两个点集。这样,其中一个合法方案就求出来了。
模型
最大权闭合子图
\qquad 对于图 G = ( V , E ) G=(V,E) G=(V,E),如果它的一个子图 G ′ = ( V ′ , E ′ ) G'=(V',E') G′=(V′,E′) 满足 V ′ V' V′ 中的任意一个点的任意一条出边都在 E ′ E' E′ 内,那么就称 G ′ G' G′ 是 G G G 的一个闭合子图。如果给每个点附上点权(可为负),那么点权最大的一个闭合子图称为最大权闭合子图。
\qquad 如果给出一个带点权的图,我们怎么求解它的最大权闭合子图呢?
\qquad 首先,我们分别建立超级源点、超级汇点,超级源点指向所有正点权的点,边权为这个点的点权;所有负点权的点指向超级汇点,边权为这个点点权的绝对值;对于原图中的边,正常建在网络上,边权为 I N F INF INF。此时,我们设所有正点权的点的点权和为 r r r。建好图之后,在图上跑一个最小割,设这个最小割的权值是 s s s,那么原图的最大权闭合子图的权值便是 r − s r-s r−s。
\qquad 例题:[NOI2006] 最大获利,太空飞行计划问题,[NOI2009] 植物大战僵尸。
最大密度子图
\qquad 我们定义一个图 G = ( V , E ) G=(V,E) G=(V,E) 的密度为 ∣ E ∣ ∣ V ∣ \frac{|E|}{|V|} ∣V∣∣E∣,最大密度子图指的便是图 G G G 中使得 ∣ E ′ ∣ ∣ V ′ ∣ \frac{|E'|}{|V'|} ∣V′∣∣E′∣ 最大的子图 G ′ = ( V ′ , E ′ ) G'=(V',E') G′=(V′,E′)。
\qquad 既然是要让一个分式最大,那么就一定要用到 0 / 1 0/1 0/1 分数规划。设当前二分的值为 g g g,那么我们就要尽可能找到 ∣ E ′ ∣ − g ∣ V ′ ∣ |E'|-g|V'| ∣E′∣−g∣V′∣ 的最大值。在求最大值的过程中,我们可以借助最小割来推导式子并求解。
\qquad 核心 C o d e Code Code:
bool check(db x) {memset(head, -1, sizeof head), tot = -1;for(int i = 1; i <= m; i ++) add(E[i].first, E[i].second, 1), add(E[i].second, E[i].first, 1);for(int i = 1; i <= n; i ++) add(S, i, m), add(i, S, m), add(i, T, 1.0 * m + 2 * x - du[i]), add(T, i, 1.0 * m + 2 * x - du[i]);//m:赋的一个偏移量return 1.0 * m * n - dinic() > 0.0;
}
最小点权覆盖集
\qquad 问题:给定一张有向图,我们现在需要覆盖这张有向图中的所有边。对于一个点 i i i,我们可以花费 W i + W_i^+ Wi+ 的代价覆盖所有指向它的边,花费 W i − W_i^- Wi− 的代价覆盖所有它指出的边,问最小需要花费多少代价?
\qquad 对于这种有向图问题,我们可以考虑拆点套路,将一个点拆成 i i i 和 i + n i+n i+n 两个点。如果是无向图,那就直接连边即可。然后我们建立超级源点,从超级源点引一条容量为 W i + W_i^+ Wi+ 的边指向点 i i i;再建立超级汇点,从 i + n i+n i+n 引一条容量为 W i − W_i^- Wi− 的边指向超级汇点。对于原图中的一条有向边 ( x , y ) (x,y) (x,y),我们引一条从 x x x 指向 y + n y+n y+n,容量为 I N F INF INF 的边。此时,我们跑出的最小割便是最小代价。
\qquad 跑完之后,我们遍历从源点指出的边。如果源点指向 v v v 的边满流了,就说明我们要选择 W u + W_u^+ Wu+;最后,我们遍历一遍所有边,如果边 ( x , y ) (x,y) (x,y) 此时没有选 W y + W_y^+ Wy+,那么我们就要选择 W x − W_x^- Wx−。这样我们就得到了一组合法方案。
最大点权独立集
\qquad 问题:给定一张图,每个点有点权,我们需要选出一些点使得这些点在没有边相连的基础上点权和最大。
\qquad 根据经典结论:最大权独立=总-最小权覆盖,所以我们还按照上一种类型建边,跑出最小覆盖后用总点权减去最小覆盖即可。
最小割建图实战
\qquad 例题:CABLETV - Cable TV Network,骑士共存问题,文理分科。
费用流
\qquad 费用流全称为“最小费用最大流”或“最大费用最大流”,它是建立在最大流的基础之上的。费用流问题中,每条边不仅有容量,还有一个费用 w w w,表示每流过单位流量,就会产生 w w w 的费用。费用流的算法基础是最大流的 E K EK EK,只不过把中间 b f s bfs bfs 的过程改为了 s p f a spfa spfa 求最短路(即最小花费)。
EK
\qquad 大体跟最大流的 E K EK EK 很像,只是改了 b f s bfs bfs 为 s p f a spfa spfa,还是很好理解的。
\qquad 核心 C o d e : Code: Code:
inline void add(int a, int b, int c, int d) {edge[++ tot] = {b, head[a], c, d}, head[a] = tot;edge[++ tot] = {a, head[b], 0, -d}, head[b] = tot;//注意,残留网络中边的费用是-d
}bool spfa() {memset(incf, 0, sizeof incf), memset(dis, 0x7f, sizeof dis);//incf:最大流量 dis:最小费用dis[S] = 0, incf[S] = INF, q.push(S), vis[S] = 1;while(!q.empty()) {int x = q.front(); q.pop(), vis[x] = 0;for(int i = head[x]; ~i; i = edge[i].lst) {int To = edge[i].to, Val = edge[i].val, Cost = edge[i].cost;if(Val && dis[To] > dis[x] + Cost) {dis[To] = dis[x] + Cost;incf[To] = min(incf[x], Val);pre[To] = i;if(!vis[To]) q.push(To), vis[To] = 1;}}}return incf[T] > 0;//判断能否跑到汇点
}void EK(int &flow, int &cost) {
[添加链接描述](https://www.luogu.com.cn/problem/P4015) while(spfa()) {flow += incf[T], cost += incf[T] * dis[T];//flow:最大流 cost:最小费用for(int i = T; i != S; i = edge[pre[i] ^ 1].to) edge[pre[i]].val -= incf[T], edge[pre[i] ^ 1].val += incf[T];}return ;
}
模型
\qquad 费用流的题目较好写(?),主要有一类是费用流与上下界最大流的结合。
费用流与上下界最大流结合
\qquad 例题:[NOI2008]志愿者招募。
\qquad 带上下界,我们仍旧采取减去下界的方式转化。但是本题还有一个最主要的问题在于:一个志愿者工作的是一段区间,是“一对多”,这是正常建边无法做到的。遇到这种情况,我们可以考虑从区间终点向区间起点连一条边,转化为无源汇可行流来做即可。
费用流建图实战
\qquad 例题:餐巾计划问题,运输问题,负载平衡问题,分配问题,深海机器人问题,数字梯形问题,K取方格数。
最小割树
\qquad 最小割树上,任意两点路径上边权最小值为这两点的最小割权值。
\qquad 模板(核心 C o d e Code Code):
void build(int l, int r) {if(l == r) return ;S = id[l], T = id[r];Add(id[l], id[r], dinic());int tmps1 = 0, tmps2 = 0;for(int i = l; i <= r; i ++) {if(d[id[i]] != -1) tmp1[++ tmps1] = id[i];else tmp2[++ tmps2] = id[i];}for(int i = l; i <= l + tmps1 - 1; i ++) id[i] = tmp1[i - l + 1];for(int i = l + tmps1; i <= r; i ++) id[i] = tmp2[i - (l + tmps1) + 1];build(l, l + tmps1 - 1), build(l + tmps1, r);
}
\qquad 例题:最小割树模板,[CQOI2016] 不同的最小割,[ZJOI2011]最小割,Pumping Stations。
相关文章:

网络流总结
网络流总结 基础知识最大流最小割定理 最大流EKdinic模型二分图匹配无源汇上下界可行流有源汇上下界最大、最小流多源汇最大流最大流之关键边最大流之拆点最大流建图实战 最小割模型最大权闭合子图最大密度子图最小点权覆盖集最大点权独立集最小割建图实战 费用流EK模型费用流与…...

安卓11通过脚本修改相应板型系统属性
安卓10以后rk的一套源码兼容很多板型,多种cpu型号都兼容了,这一点相比之前省心了很多,所以就诞生了需要一套代码兼容多种板子的需求,定制修改中需要经常修改系统属性,通过以下脚本一次实现: #!/bin/bashfu…...
网络安全—PKI公钥基础设施
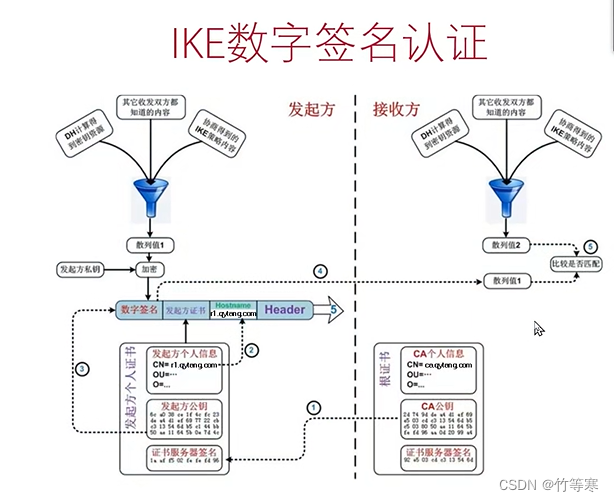
文章目录 前提知识散列函数非对称加密数字签名 PKI受信任的人RA注册CA颁发IKE数字签名认证(交换证书)密钥管理 前提知识 散列函数 散列也可以叫哈希函数,MD5、SHA-1、SHA-2、、(不管叫啥,都记得是同一个东西就行&…...
推荐一款加速器,也可加速github
地址https://github.com/BeyondDimension/SteamTools...

springboot框架,中间库是mognodb,可以写入2个数据库的Demo
1-springboot版本: 2.3.9.RELEASE POM.xml文件: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance&quo…...
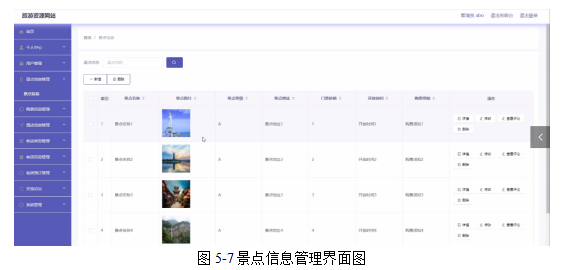
基于Java SSM框架实现旅游资源网站系统项目【项目源码+论文说明】
基于java的SSM框架实现旅游资源网站系统演示 摘要 本论文主要论述了如何使用JAVA语言开发一个旅游资源网站 ,本系统将严格按照软件开发流程进行各个阶段的工作,采用B/S架构,面向对象编程思想进行项目开发。在引言中,作者将论述旅…...

015、控制流运算符match
1. 控制流运算符match Rust中有一个异常强大的控制流运算符:match,它允许将一个值与一系列的模式相比较,并根据匹配的模式执行相应代码。模式可由字面量、变量名、通配符和许多其他东西组成;后文会详细介绍所有不同种类的模式及它…...

个人博客主题 vuepress-hope
文章目录 1. 简介2. 配置2.1 个人博客,社媒链接配置 非常推荐vuepress-hope 1. 简介 下面的我的博客文章的截图 通过md写博客并且可以同步到github-page上 2. 配置 2.1 个人博客,社媒链接配置 配置文件 .vuepress/theme.ts blog: {medias: {BiliB…...
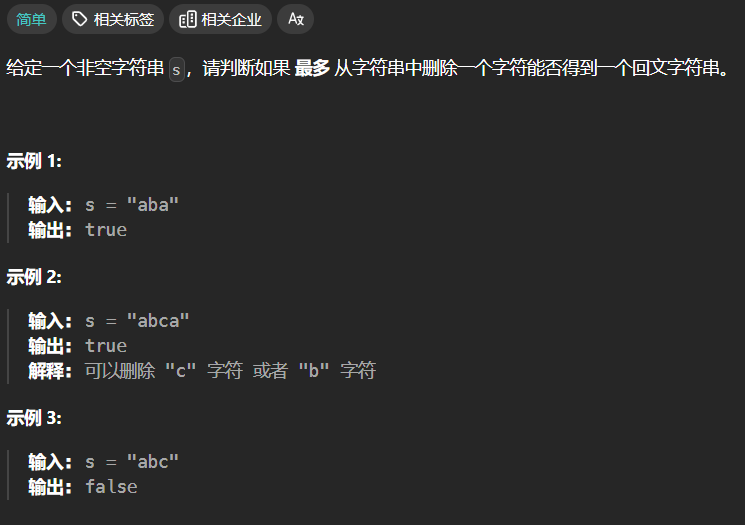
【LeetCode-剑指offer】--19.验证回文串II
19.验证回文串II 方法:双指针 首先考虑如果不允许删除字符,如何判断一个字符串是否是回文串。常见的做法是使用双指针。定义左右指针,初始时分别指向字符串的第一个字符和最后一个字符,每次判断左右指针指向的字符是否相同&#…...
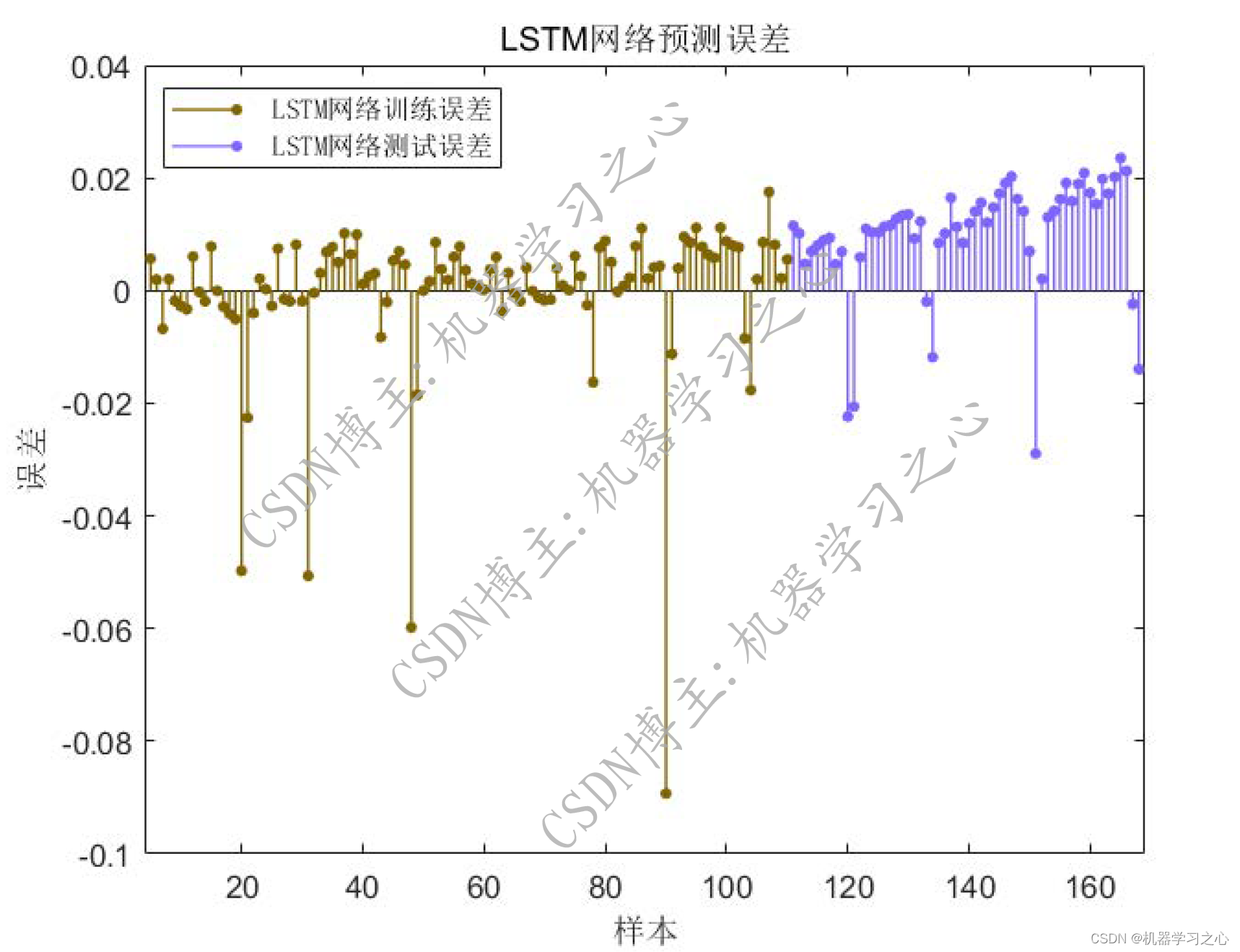
锂电池寿命预测 | Matlab基于LSTM长短期记忆神经网络的锂电池寿命预测
目录 预测效果基本介绍程序设计参考资料 预测效果 基本介绍 锂电池寿命预测 | Matlab基于LSTM长短期记忆神经网络的锂电池寿命预测 程序设计 完整程序和数据获取方式:私信博主回复Matlab基于LSTM长短期记忆神经网络的锂电池寿命预测。 参考资料 [1] http://t.csdn…...

JSON 详解
文章目录 JSON 的由来JSON 的基本语法JSON 的序列化简单使用stringify 方法之 replacerstringify 方法之 replacer 参数传入回调函数stringify 方法之 spacestringify 方法之 toJSONparse 方法之 reviver 利用 stringify 和 parse 实现深拷贝 json 相信大家一定耳熟能详&#x…...

我不想学JAVA---------JAVA和C的区别
前言 我一个研究方向是SLAM的为什么要来学JAVA。 从九月份开学到现在,已经学了Linux,数据结构,SLAM,C的基础操作,期间还参与编写了一本VHDL的教材。还有上课、考试什么的其他杂七杂八的事情就不说了。 读研好苦逼&…...
不能错过的AI前沿开源工具!
🌈🌈🌈🌈🌈🌈🌈🌈 欢迎关注公众号(通过文章导读关注:【11来了】),及时收到 AI 前沿项目工具及新技术 的推送 发送 资料 可领取 深入理…...

为什么深度学习神经网络可以学习任何东西
下图你所看到的,是著名的曼德尔布罗特集,我们可以见证这个集合呈现出的复杂形态: 要理解神经网络如何学习曼德尔布罗特集,我们首先需要从最基础的数学概念讲起:什么是函数?函数本质上是一个将输入转化为输出…...
使用 SpringSecurity 发送POST请求出现 403
问题场景 在使用 SpringSecurity 时对一些访问权限进行了设置, 在用户请求资源时出现了403错误 , 通过检查代码发现请求权限是开放的, 并且切换成 GET 请求也是可以通过, 换成POST 请求就无法通过。 解决方法 在 SpringSecurity 中关闭 CSRF 因为 前端向后台发送 post 请求…...
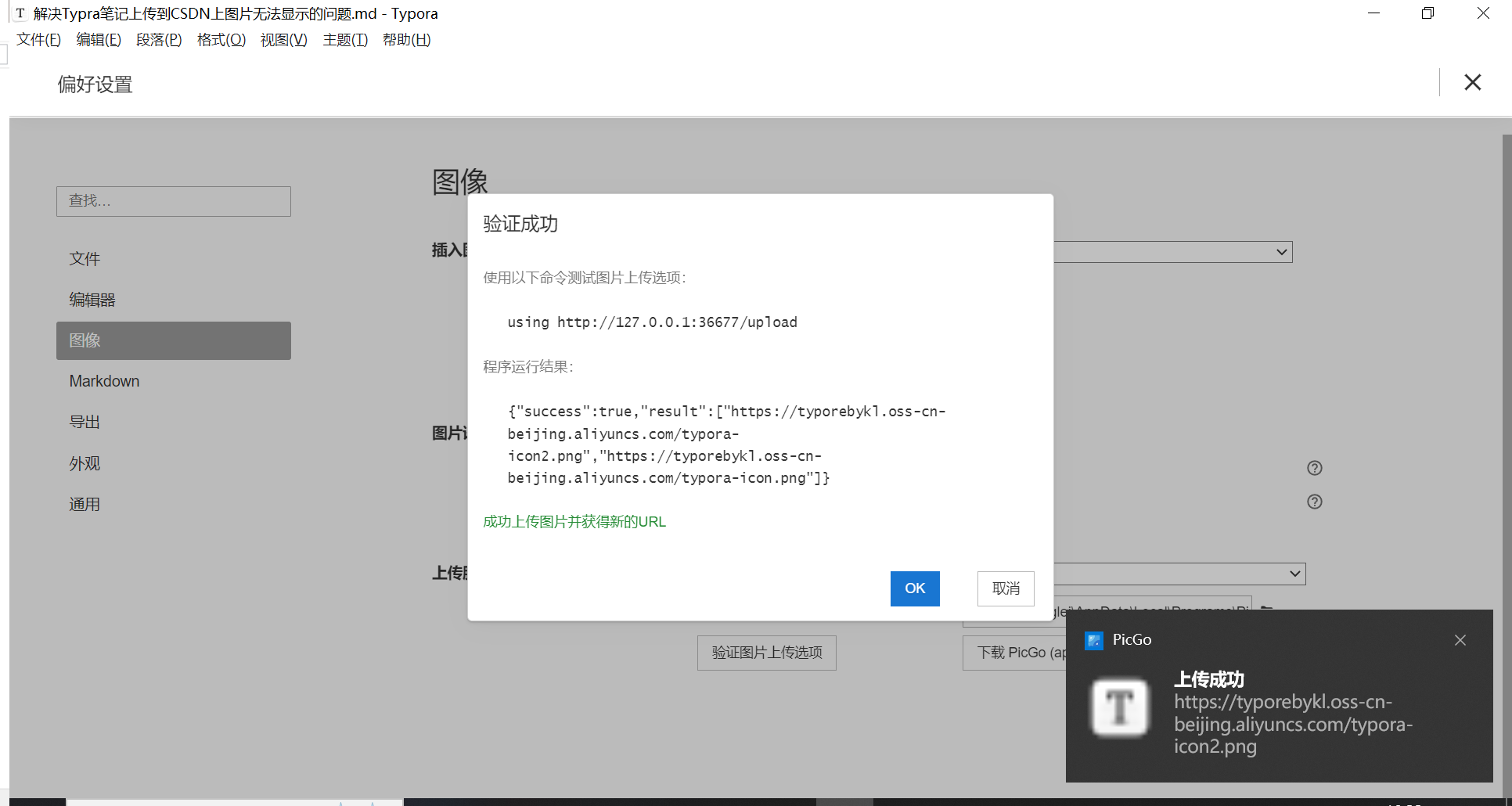
解决Typora笔记上传到CSDN上图片无法显示的问题
解决Typora笔记上传到CSDN上图片无法显示的问题 一、发现问题二、分析问题三、解决问题图床介绍所需工具PicGo软件安装操作下载安装PicGo配置PicGo 设置Typora 四、总结 一、发现问题 当我们使用Typora这款强大的Markdown编辑器记录笔记时,经常会遇到一个让人困扰的…...
)
Vue3.0+Echarts (可视化界面)
Vue3.0Echarts (可视化界面) 1. 简介2. 安装2.1 下载安装Node.js2.2 全局下载项目脚手架2.3 创建项目 1. 简介 2. 安装 2.1 下载安装Node.js 2.2 全局下载项目脚手架 以管理员身份执行 npm install -g vue/cli vue --version2.3 创建项目 vue crea…...

编程语言的未来:探索技术进步的轨迹
编程语言的未来:探索技术进步的轨迹 随着科技的飞速发展,编程语言在计算机领域中扮演着至关重要的角色。它们是软件开发的核心,为程序员提供了与机器沟通的桥梁。然而,未来的技术进步将如何影响编程语言的走向呢?让我…...
SOLIDWORKS使用技巧——SOLIDWORKS草图绘制时一定要完全定义
SOLIDWORKS草图的定义状态有多种,按是否报错区分,如下: 1. 正常状态:欠定义、完全定义; 2. 错误状态的:过定义、悬空、无解; 其中,错误状态需要修复,不然会影响模型重…...
网络类型之GRE和MGRE和NHRP
GRE-通用路由封装 是一种简单的三层VPN封装技术,属于虚拟的点到点网络类型 优点:支持IP 网络作为承载网络、支持多种协议、支持IP 组播,配置简单,容易布署。 缺点:缺少保护功能,不能执行如认证、加密、以…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...
