“华为杯”杭州电子科技大学2023新生编程大赛---树
题目链接
Problem Description
给定一棵包含 n 个节点的带边权的树,树是一个无环的无向联通图。定义 xordist(u,v) 为节点 u 到 v 的简单路径上所有边权值的异或和。
有 q 次询问,每次给出 `l r x`,求 ∑ri=lxordist(i,x) 的值。
Input
测试点包含多组数据。第一行包含一个整数 T(1≤T≤10),表示数据组数。每组数据的输入格式如下:
第一行包含一个整数 n(1≤n≤105),表示节点的个数。
接下来 n−1 行,每行包含三个整数 u、v 和 w(1≤u,v≤n,0≤w<230),表示 u 和 v 之间存在一条权值为 w 的无向边。保证输入是一棵树。
接下来一行,包含一个整数 q(1≤q≤105),表示询问的次数。
接下来 q 行,每行包含三个整数 l、r 和 x(1≤l≤r≤n,1≤x≤n),分别表示每次询问的信息,其含义已在上文说明。
Output
每组数据包含 q 行,每行一个整数,表示每次询问的答案。
题意:
定义了一个函数 xordist(u,v) 为节点 u 到 v 的简单路径上所有边权值的异或和。
给你多次询问,求有 q 次询问,每次给出 l, r, x,求 xordist(i,x) 的值。
思路:
首先可以知道,我们任意选一点为根 root 往下递归异或就可以得到 f [ i ](root 到 i 的路径异或值 ),那么 l 到 r 的路劲异或值可以由 f [ l ] ^ f [ r ]得出;
那么如何计算答案呢,就是用 f [ l ]~f [ r ] 分别异或f [ x ] 相加即可,但是1e5级别的询问显然时间复杂度不可以接受,然后我们就行有什么可以快速算出 l ~ r 的贡献呢,这时候就看思维发不发散了,这里可以想到用前缀和;
(当然不是异或前缀和,异或不满足分配律,比如 (2^3+2^3+4^3)!=8^3
所以是另一种 :计算1~n , f [ i ] 2进制的每一位1和0的前缀和,
那么答案就是,对f [ x ] 的每一位的贡献计算,比如f [ x ] 第2位是0,那么根据异或1异或0才有贡献, 贡献就是 pow( 2 , i (第几位) )*( sum1[ r ][ i ]-sum1[ l-1 ][ i ] );
复杂度位1e5*30,显然可以接受
完毕
int n;
int f[N];
vector<PII> g[N];
void dfs(int u, int fa)
{for (auto ed : g[u]){if (ed.xx == fa)continue;f[ed.xx] = f[u] ^ ed.yy;dfs(ed.xx, u);}
}
int qpow(int a, int b)
{int res = 1;while (b){if (b & 1)res = res * a;a = a * a;b >>= 1;}return res;
}
void solve()
{cin >> n;for (int i = 1; i <= n; i++){g[i].clear();f[i] = 0;}int root = inf;for (int i = 1; i <= n - 1; i++){int a, b, c;cin >> a >> b >> c;g[a].pb({b, c});g[b].pb({a, c});root = min({a, b, root});}dfs(root, -1);vector<vector<int>> sum1(n + 2, vector<int>(32));vector<vector<int>> sum0(n + 2, vector<int>(32));for (int i = 1; i <= n; i++){for (int j = 0; j <= 29; j++){int x = (f[i] >> j & 1);if (x)sum1[i][j]++;elsesum0[i][j]++;sum1[i][j] += sum1[i - 1][j];sum0[i][j] += sum0[i - 1][j];}}int q;cin >> q;while (q--){int l, r, x;cin >> l >> r >> x;int ans = 0;for (int i = 0; i <= 29; i++){int t = (f[x] >> i & 1);if (t)ans += qpow(2, i) * (sum0[r][i] - sum0[l - 1][i]);elseans += qpow(2, i) * (sum1[r][i] - sum1[l - 1][i]);}cout << ans << endl;}
}
signed main()
{Yshanqian;int T;T = 1;cin >> T;for (int cases = 1; cases <= T; ++cases){// cout<<"Case #"<<cases<<": ";solve();}return 0;
}
相关文章:
“华为杯”杭州电子科技大学2023新生编程大赛---树
题目链接 Problem Description 给定一棵包含 n 个节点的带边权的树,树是一个无环的无向联通图。定义 xordist(u,v) 为节点 u 到 v 的简单路径上所有边权值的异或和。 有 q 次询问,每次给出 l r x,求 ∑rilxordist(i,x) 的值。 Input 测试…...
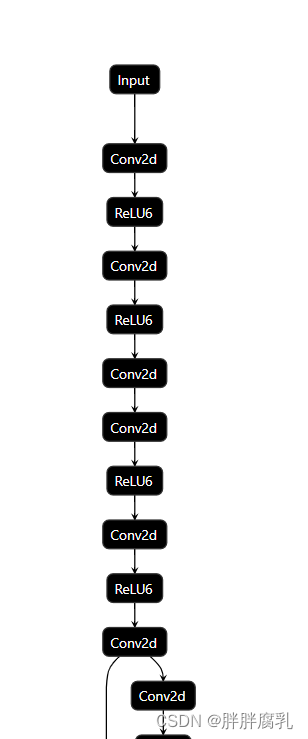
使用pnnx将Torch模型转换为ncnn
1. 引言 以往我们将Torch模型转换为ncnn模型,通常需经过Torch–>onnx,onnx–>ncnn两个过程。但经常会出现某些算子不支持的问题。 ncnn作者针对该问题,直接开发一个Torch直接转换ncnn模型的工具 (PNNX),以下为相关介绍及使…...

linux卸载小皮面板phpstudy教程
千万不要直接删文件夹! 千万不要直接删文件夹! 千万不要直接删文件夹! 我就是按照网上搜索的教程,直接删了,然后 系统就不停的崩溃 生成这种文件: -rw------- 1 root root 223M Dec 28 22:36…...
【萤火虫系列教程】1/5-Adobe Firefly 注册账号
001-Adobe Firefly 注册账号 AI时代如火如荼,Adobe也不甘落后,于今年3月份发布AI创意生成工具Firefly(中文翻译:萤火虫) Adobe Firefly简介 Adobe Firefly的官方介绍为:Firefly是Adobe产品中新的创意生成…...

【docker】Dockerfile 指令详解
一、Dockerfile 指令详解 Dockerfile是一个用于编写docker镜像生成过程的文件,其有特定的语法。Dockerfile的基本指令有十三个,分别是:FROM、MAINTAINER、RUN、CMD、EXPOSE、ENV、ADD、COPY、ENTRYPOINT、VOLUME、USER、WORKDIR、ONBUILD。 …...

内存管理机制
内存管理机制与内存映射相关。 一、C与C 之所以将C与C放在一起是因为C是C的超集; 但是C是面向过程语言,C是面向对象的语言; C与C都可以使用malloc、calloc、realloc来申请内存空间; 其中void* malloc(size_t size)是在内存的动态…...
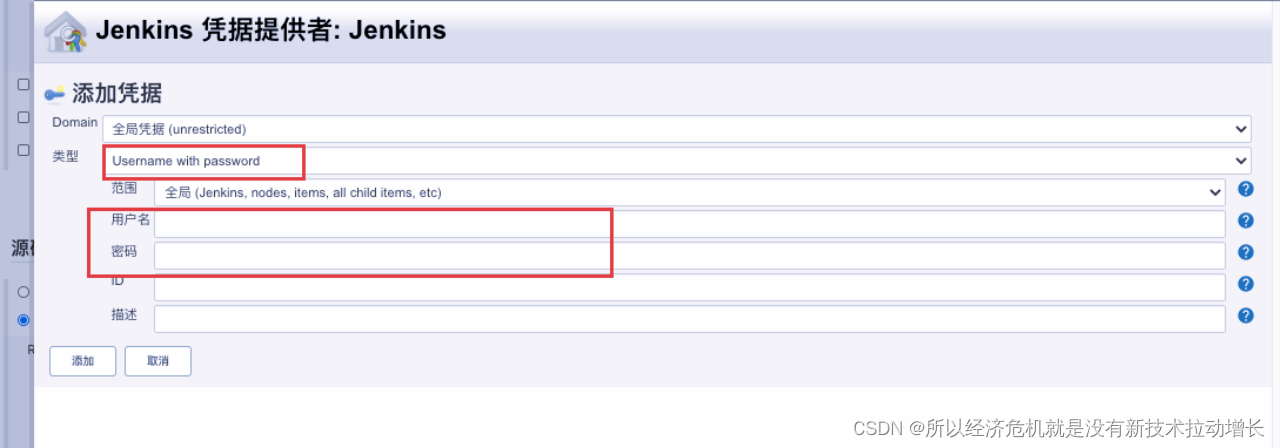
Jenkins工具使用
学习目录: 1、jenkins的安装 2、junkins的常规使用 3、jenkins在接口自动化测试实践 具体内容: 1、jenkins的安装 安装包下载:推荐Index of /jenkins/war/latest/ | 清华大学开源软件镜像站 | Tsinghua Open Source Mirror,…...

SpringBoot从配置文件中获取属性的方法
方式一:Value 基本类型属性注入,直接在字段上添加Value("${xxx.xxx}")即可.注意这里用的是$,而不是#,Value注入的属性,一般其他属性没有关联关系。 配置文件 user:name: Manaphyage: 19sex: m…...
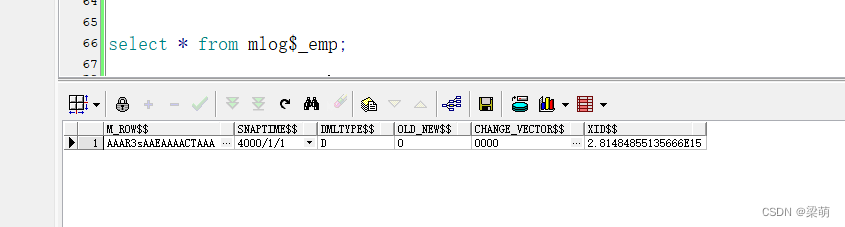
oracle物化视图
物化视图定义 视图是一个虚拟表(也可以认为是一条语句),基于它创建时指定的查询语句返回的结果集,每次访问它都会导致这个查询语句被执行一次,为了避免每次访问都执行这个查询,可以将这个查询结果集存储到…...

基于ssm校园线上订餐系统的设计与实现论文
摘 要 信息数据从传统到当代,是一直在变革当中,突如其来的互联网让传统的信息管理看到了革命性的曙光,因为传统信息管理从时效性,还是安全性,还是可操作性等各个方面来讲,遇到了互联网时代才发现能补上自古…...
鸿蒙南向开发—OpenHarmony技术编译构建框架
概述 OpenHarmony编译子系统是以GN和Ninja构建为基座,对构建和配置粒度进行部件化抽象、对内建模块进行功能增强、对业务模块进行功能扩展的系统,该系统提供以下基本功能: 以部件为最小粒度拼装产品和独立编译。支持轻量、小型、标准三种系…...
Android Jetpack学习系列——Navigation
写在前面 Google在2018年就推出了Jetpack组件库,但是直到今天我才给重视起来,这真的不得不说是一件让人遗憾的事。过去几年的空闲时间里,我一直在尝试做一套自己的组件库,帮助自己快速开发,虽然也听说过Jetpack&#…...

编程语言的新趋势
随着科技的飞速发展,IT行业经历了巨大的变革,其中编程语言作为技术生态的核心要素,其演变趋势对整个行业影响深远。从过去到现在,再到未来,编程语言的发展都呈现出明显的时代特征。本文将探讨当前IT行业的现状…...
)
C++:类和对象(2)
目录 1.strcut和class的区别 2.将成员属性设置为私有 3.对象的初始化和清理 3.1 构造函数和析构函数 3.1.1 构造函数语法 3.1.2 析构函数语法 3.1.3 检验 3.2 构造函数的分类和调用 3.3 拷贝构造函数调用 1.strcut和class的区别 struct和class的唯一区别在于默认的访问…...
【React系列】网络框架axios库的使用
本文来自#React系列教程:https://mp.weixin.qq.com/mp/appmsgalbum?__bizMzg5MDAzNzkwNA&actiongetalbum&album_id1566025152667107329) 一. axios库的基本使用 1.1. 网络请求的选择 目前前端中发送网络请求的方式有很多种: 选择一:传统的Aj…...
pygame学习(二)——绘制线条、圆、矩形等图案
导语 pygame是一个跨平台Python库(pygame news),专门用来开发游戏。pygame主要为开发、设计2D电子游戏而生,提供图像模块(image)、声音模块(mixer)、输入/输出(鼠标、键盘、显示屏)模…...
)
TCL学习笔记(持续更新)
前言: TCL(tool common language)是一种通用工具语言,很多eda tool都支持tcl,学习了解一些tcl基本语法还是很有必要的。 1:基础概念 解释器: #!/usr/bin/tclsh 打印: puts -> p…...
的元素,用//表达式匹配不到(附解决办法))
Xpath的问题:为什么在DOM中确定存在(可见)的元素,用//表达式匹配不到(附解决办法)
今天遇到一个很有意思的问题,我的爬取的目标页面上有时会出现一个弹窗,它挡住我点击其它按钮了,我想找到它的关闭按钮,自动点击一下关闭掉,本来是很简单的事情,但偏偏出问题了,DOM中看到的html是…...

有没有游泳可以戴的耳机?游泳耳机入耳式好,还是骨传导好
游泳是一项既能锻炼身体又能让人放松心情的运动。我们知道,音乐能够为我们的水上时光增添更多的乐趣。那么,在众多游泳耳机中,如何选择一款既适合自己的需求又具备良好性能的产品呢? 首先,我们要了解的是,…...

【绘图软件】自用安装教程
链接:https://pan.baidu.com/s/17r9Pr460FzkULU7fTr91_w?pwdftv7 提取码:ftv7 --来自百度网盘超级会员V6的分享解压并且右键打开set up 解压crack软件前需要退出杀毒软件, 关闭实时保护 域网络关闭,专用网络关闭࿰…...

Mish激活函数改进YOLOv26平滑非线性映射与自正则化特性双重突破
Mish激活函数改进YOLOv26平滑非线性映射与自正则化特性双重突破 摘要 在深度学习目标检测领域,激活函数作为神经网络的核心非线性组件,直接影响模型的表达能力和收敛性能。本文提出基于Mish激活函数的YOLOv26改进方案,通过引入平滑、无上界…...

Field II 超声相控阵仿真系列:多角度平面波相干合成提升成像质量
1. 从“快”到“好”:为什么单次平面波成像不够用? 大家好,我是老张,在超声成像仿真这个领域摸爬滚打了十来年,用过不少工具,Field II算是我的老朋友了。今天咱们不聊那些复杂的理论推导,就说说…...
用EB配置MCAL:从零到一构建AUTOSAR基础软件层)
S32K1XX系列单片机 ——(2)用EB配置MCAL:从零到一构建AUTOSAR基础软件层
1. 写在前面:为什么你需要这份“避坑”指南? 你好,我是老张,一个在嵌入式行业摸爬滚打了十几年的老工程师。从早期的51、AVR,到后来的STM32,再到现在的AUTOSAR,我几乎把新手能踩的坑都踩了一遍。…...
✅)
计算机毕业设计源码:Spark闲鱼二手商品数据智能分析平台 Hadoop Vue 可视化 协同过滤推荐算法 电商 商品 数据分析 大模型 大数据(建议收藏)✅
博主介绍:✌全网粉丝10W,前互联网大厂软件研发、集结硕博英豪成立软件开发工作室,专注于计算机相关专业项目实战6年之久,累计开发项目作品上万套。凭借丰富的经验与专业实力,已帮助成千上万的学生顺利毕业,…...

2026,AI创业者的慷慨、残酷与迷雾:从历史规律看价值迁移
当代码被商品化,你的护城河在哪里?2026年2月,前Tesla AI总监、OpenAI创始成员Andrej Karpathy在X上分享了一个个人观察:11月,他的编程工作还是80%手写代码、20%让AI agent处理;到了12月,比例完全…...

手搓51单片机+ADC0808电压表:从焊板子到显示数值全攻略
51单片机和ADC0808数字电压表,包括程序源码和protues仿真,pcb等,程序源码注释详细,适合单片机开发人员和新手。最近在工作室翻出几片落灰的ADC0808,这老伙计可是当年做课程设计的标配。今天带大家用STC89C52做个真能用…...

2026美妆行业自动图文发布工具推荐指南
2026美妆行业自动图文发布工具推荐指南行业背景与推荐依据据《2025年美妆行业数字化营销白皮书》显示,美妆行业线上营销投入占比已达68%,其中小红书、抖音两大平台的内容营销贡献了超过70%的线上获客量。随着内容营销的深化,美妆品牌普遍面临…...

好软推荐-自用软件
目录导航PC应用OFFICE办公系列万彩办公大师http://www.wofficebox.com/办公必备的小工具百宝箱。iSlide插件PPT插件 [https://www.islide.cc/](https://www.islide.cc/)官方口号:让PPT设计简单起来!方方格子Excel插件 [http://www.ffcell.com/](http://w…...

2023最新版:用夜神模拟器安卓7抓包微信小程序的3个关键配置
2023版实战指南:攻克高版本微信小程序抓包,从模拟器选型到证书植入的深度解析 最近在测试一个电商类微信小程序时,遇到了一个老问题的新挑战:抓包工具突然“失灵”了。小程序页面加载正常,但关键的API请求数据在Burp S…...

不用Firebase也能实现Google登录?对比原生Android与FirebaseAuth两种方案
告别Firebase依赖:深度解析Android原生Google登录方案与FirebaseAuth的抉择 最近在重构一个老项目时,我遇到了一个经典的技术选型问题:用户认证模块。团队里有人坚持使用Firebase Authentication,认为它省心省力;也有…...
