C语言-蓝桥杯2023年第十四届省赛真题-砍树
题目描述
给定一棵由 n 个结点组成的树以及 m 个不重复的无序数对 (a1, b1), (a2, b2),
. . . , (am, bm),其中 ai 互不相同,bi 互不相同,ai ≠ bj(1 ≤ i, j ≤ m)。
小明想知道是否能够选择一条树上的边砍断,使得对于每个 (ai , bi) 满足 ai和 bi 不连通,如果可以则输出应该断掉的边的编号(编号按输入顺序从 1 开始),否则输出 -1.
输入格式
输入共 n + m 行,第一行为两个正整数 n,m。
后面 n − 1 行,每行两个正整数 xi,yi 表示第 i 条边的两个端点。
后面 m 行,每行两个正整数 ai,bi。
输出格式
一行一个整数,表示答案,如有多个答案,输出编号最大的一个。
样例输入
6 2 1 2 2 3 4 3 2 5 6 5 3 6 4 5 4
样例输出
4
提示
断开第 2 条边后形成两个连通块:{3, 4},{1, 2, 5, 6},满足 3 和 6 不连通,4 和 5 不连通。
断开第 4 条边后形成两个连通块:{1, 2, 3, 4},{5, 6},同样满足 3 和 6 不连通,4 和 5 不连通。
4 编号更大,因此答案为 4。
对于 30% 的数据,保证 1 < n ≤ 1000。
对于 100% 的数据,保证 1 < n ≤ 105,1 ≤ m ≤ 2/n。
解题:
#include <iostream>
#include <queue>
#include <map>
#include <set>
#include <stack>
#include <string>
#include<functional>
#include <math.h>
#include <algorithm>
#include<unordered_map>
#include<ctime>
#include <cstring>
#define lowbit(x) (-x) & x
#define ll long long
const int N = 3e6;
using namespace std;
const int mod = 1e9 + 7;
ll __pow(ll x,ll y){ll res = 1;while(y){if(y&1)res = (res * x);y>>=1;x = (x * x);}return res;
}
ll cal(ll v1, ll v2){return v1*__pow(v2,mod-2)%mod;
}
ll C(ll x,ll y){ll res = 1;for(int i = 1,j = x + 1; j <= y;j++, i++){res*=j;res/=i;}return res;
}
ll gcd(ll x, ll y){if(y == 0)return x;else return gcd(y, x%y);
}
struct node{int to,nxt,c = 0,idx;
}e[N];
int cnt = 0;
int head[N];
void add(int u, int v){e[++cnt].nxt = head[u];e[cnt].to = v;head[u] = cnt;e[cnt].c = 0;e[cnt].idx = (cnt + 1)/2;
}
void solve(){ int n,m;cin>>n>>m;for(int i = 0; i < n - 1; ++i){int u,v;cin>>u>>v;u--,v--;add(u, v);add(v, u);}map<ll,int>lca;vector<int>query[n];for(int i = 0; i < m;++i){int u, v;cin>>u>>v;u--, v--;query[u].push_back(v);query[v].push_back(u);} int p[n];int f[n];vector<int>diff(n, 0);vector<int>color(n, 0);for(int i = 0; i < n;++i)f[i] = i;function<int(int)>find = [&](int x)->int{return (f[x] == x)?x : f[x] = find(f[x]);};function<void(int,int)>tarjan = [&](int u,int fa){color[u] = 1;p[u] = fa;for(int i = head[u];i ; i = e[i].nxt){int v = e[i].to;if(color[v]==0){tarjan(v, u);f[v] = u;}}for(int v : query[u]){if(color[v]==2 || u == v){int ffa = find(v);diff[u]++;diff[v]++;lca[(ll)u*(1ll<<32) + v] = ffa;lca[(ll)v*(1ll<<32) + u] = ffa;diff[ffa]-=2;}}color[u] = 2;};tarjan(0, -1);int maxe = -1;function<void(int,int)>dfs = [&](int u, int fa){for(int i = head[u];i; i = e[i].nxt){int v = e[i].to;if(v == fa)continue;dfs(v, u);int id = e[i].idx;diff[u] += diff[v]; if(diff[v] == m){maxe = max(maxe, id);}} };dfs(0, -1);cout<<maxe<<endl;
}
int main(){ ios::sync_with_stdio(false);cout.tie(0);cin.tie(0);int t;t = 1;while(t--){solve();}return 0 ;
}相关文章:

C语言-蓝桥杯2023年第十四届省赛真题-砍树
题目描述 给定一棵由 n 个结点组成的树以及 m 个不重复的无序数对 (a1, b1), (a2, b2), . . . , (am, bm),其中 ai 互不相同,bi 互不相同,ai ≠ bj(1 ≤ i, j ≤ m)。 小明想知道是否能够选择一条树上的边砍断,使得对于每个 (a…...
python识别验证码+灰度图片base64转换图片
一、为后面识别验证码准备 1、base64转换为图片,保存本地、并且置灰 上文中的base64,后面的就是包含Base64编码的PNG图像的字符串复制下来 import base64 from PIL import Image import io# 这里是你的Base64编码的字符串 base64_data "iVBORw0KGgoAAAANSUhE…...
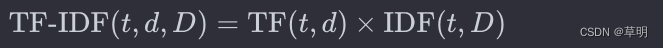
TF-IDF(Term Frequency-Inverse Document Frequency)算法 简介
TF-IDF(Term Frequency-Inverse Document Frequency)是一种用于信息检索和文本挖掘的常用算法。它用于评估一个词对于一个文档集合中某个文档的重要性。 这个算法的基本思想是:如果一个词在一个文档中频繁出现,并且在整个文档集合…...

企业怎么打造私域转化闭环?
一、私域矩阵构建 1、公众号 (1)流量来源:微信公众号既是私域流量的起点,亦为其源源不断的提供流量支持; (2)内容展示:公众号作为内容发布的主要渠道,可以通过公众号传…...

基于等保合规和滑动标尺模型的云安全建设方法
文章目录 前言一、云计算平台面临的安全挑战(一)新兴风险和传统风险的冲击(二) 云计算安全日益严峻,面临更大的安全挑战(三)提升对云计算平台的全面系统性安全建设的认知二、在云计算安全建设上的误区(一)缺乏整体视角构建云上安全,安全及运营存在割裂(二) 缺乏云内…...

MySQL数据库期末知识点总结(复习版)
一、数据库基本知识 数据库中的数据有什么特点 1、数据是按某种结构组织的 2、数据有整体性、共享性和较高的独立性 数据管理技术经历了哪三个阶段 1、手工管理 2、文件管理 3、数据库管理 数据库管理系统的主要功能有哪些 数据库管理系统的主要功能包括数据定义、数据…...
流行的Jmeter+Ant+Jenkins接口自动化测试框架在网络上走红
大致思路:Jmeter可以做接口测试,也能做压力测试,而且是开源软件;Ant是基于Java的构建工具,完成脚本执行并收集结果生成报告,可以跨平台,Jenkins是持续集成工具。将这三者结合起来可以搭建一套We…...

MySQL 数据页损坏处理思路
文章目录 前言1. 备份恢复2. 强制 InnoDB 恢复2.1 损坏数据页2.2 观察错误日志2.3 设置参数2.4 定位表信息2.5 分析处理2.6 恢复数据 总结 前言 研发自己搭建了一套 MySQL 没有设置双一参数,机房异常断电,导致数据页出现损坏,本篇文章介绍此…...

面试 Vue 框架八股文十问十答第二期
面试 Vue 框架八股文十问十答第二期 作者:程序员小白条,个人博客 相信看了本文后,对你的面试是有一定帮助的!关注专栏后就能收到持续更新! ⭐点赞⭐收藏⭐不迷路!⭐ 1)常见的事件修饰符及其作…...

【Python学习】2024PyCharm插件推荐
目录 【Python学习】2024PyCharm插件推荐 1. Key Promoter X2.Rainbow CSV3.Markdown4.Rainbow Brackets5.Indent Rainbow6.Regex Tester7.Regex Tester8.Background Image Plus9.Material Theme UI10. Chinese 汉化插件参考 文章所属专区 Python学习 1. Key Promoter X 方便…...

剑指offer题解合集——Week2day6
文章目录 剑指offerWeek2周六:表示数值的字符串AC代码思路: 周六:调整数组顺序使奇数位于偶数前面AC代码思路: 剑指offerWeek2 周六:表示数值的字符串 题目链接:表示数值的字符串 请实现一个函数用来判…...

算法训练第五十二天|300. 最长递增子序列、674. 最长连续递增序列、718. 最长重复子数组
300. 最长递增子序列: 题目链接 给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。 子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组…...

HTTP基础知识总结
目录 一、什么是HTTP? 二、与HTTP有关的协议 三、HTTP请求特征 四、HTTP组成格式 五、HTTP标头 1.通用标头 2.实体标头 3.请求标头 4.响应标头 六、HTTP状态码分类 我们在日常测试过程中,也可以通过浏览器F12简单定位是前端问题还是后端问题&a…...
创意与技术的结晶:AI魔法绘图与中文描述的完美结合
在人类文明的长河中,创意与技术一直是推动发展的重要动力。随着科技的日新月异,人工智能(AI)在创意领域的应用逐渐崭露头角,而AI魔法绘图与中文描述的结合,更是将这一趋势推向了新的高度。AI魔法绘图是一种…...
)
Python:int(value, base=10)
int(value, base2) 是 Python 中的一个内置函数,用于将一个字符串或数字以指定的进制转换为整数。 函数的参数含义如下: value:要进行转换的值,可以是一个字符串或数字。base:进制数,默认为 10࿰…...
)
Vue之调用store的action(包含getter调用)
文章目录 Vue之调用store的action(包含getter调用)调用store的action方法一:Promise 链式调用方法二:async/await方法三:Promise.all()同时执行 调用store的getter方法一:this.$store.getters调用方法二:mapGetters调用…...

蟹目标检测数据集VOC格式400张
蟹,一种独特的海洋生物,以其强壮的身体和独特的生活习性而闻名。 蟹的身体宽厚,有一对锐利的大钳子,这使得它们在寻找食物和保护自己时非常有力。蟹的外观颜色多样,有绿色、蓝色、棕色和红色等,这使得它们在…...

PyTorch中常用的工具(4)Visdom
文章目录 前言3.2 Visdom 前言 在训练神经网络的过程中需要用到很多的工具,最重要的是数据处理、可视化和GPU加速。本章主要介绍PyTorch在这些方面常用的工具模块,合理使用这些工具可以极大地提高编程效率。 由于内容较多,本文分成了五篇文…...
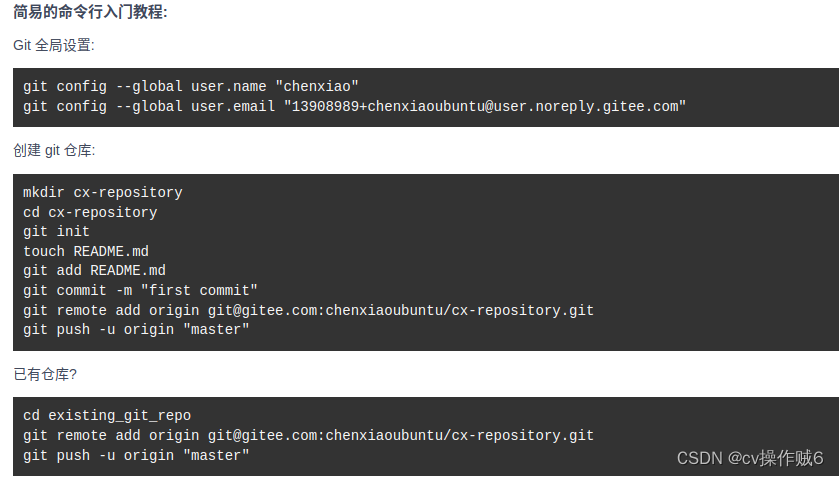
Linux(ubuntu)下git / github/gitee使用
先附上git命令 linuxchenxiao:~$ cd Templates/ 先进入一个目录,也可mkdir新建一个目录:用于接下来初始化为git可以管理的仓库 这个目录就是所说的工作目录,指当前正在进行开发的项目的本地目录。 linuxchenxiao:~/Templates$ git init 已…...
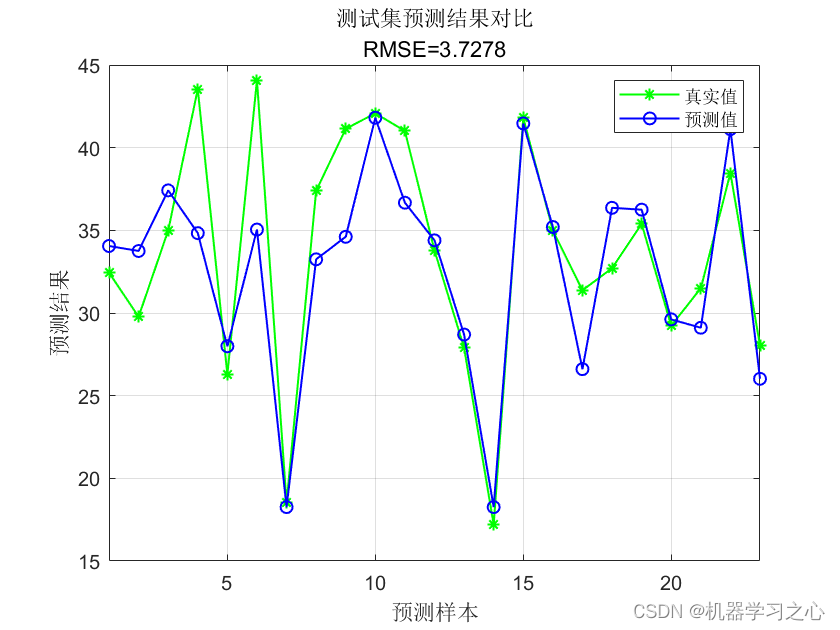
回归预测 | MATLAB实OOA-LSTM基于鱼鹰优化算法优化长短期记忆网络的多输入单输出数据回归预测模型 (多指标,多图)
回归预测 | MATLAB实OOA-LSTM基于鱼鹰优化算法优化长短期记忆网络的多输入单输出数据回归预测模型 (多指标,多图) 目录 回归预测 | MATLAB实OOA-LSTM基于鱼鹰优化算法优化长短期记忆网络的多输入单输出数据回归预测模型 (多指标&a…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...
