[足式机器人]Part2 Dr. CAN学习笔记-自动控制原理Ch1-8Lag Compensator滞后补偿器
本文仅供学习使用
本文参考:
B站:DR_CAN
Dr. CAN学习笔记-自动控制原理Ch1-8Lag Compensator滞后补偿器
从稳态误差入手(steady state Error)

误差 Error : E ( s ) = R ( s ) − X ( s ) = R ( s ) − E ( s ) ⋅ K G ( s ) ⇒ E ( s ) ( 1 + K G ( s ) ) = R ( s ) ⇒ E ( s ) = 1 1 + K G ( s ) R ( s ) = R ( s ) 1 1 + K N ( s ) D ( s ) = 1 s 1 1 + K N ( s ) D ( s ) E\left( s \right) =R\left( s \right) -X\left( s \right) =R\left( s \right) -E\left( s \right) \cdot KG\left( s \right) \Rightarrow E\left( s \right) \left( 1+KG\left( s \right) \right) =R\left( s \right) \Rightarrow E\left( s \right) =\frac{1}{1+KG\left( s \right)}R\left( s \right) =R\left( s \right) \frac{1}{1+K\frac{N\left( s \right)}{D\left( s \right)}}=\frac{1}{s}\frac{1}{1+K\frac{N\left( s \right)}{D\left( s \right)}} E(s)=R(s)−X(s)=R(s)−E(s)⋅KG(s)⇒E(s)(1+KG(s))=R(s)⇒E(s)=1+KG(s)1R(s)=R(s)1+KD(s)N(s)1=s11+KD(s)N(s)1
单位阶跃unit step : R ( s ) = 1 s R\left( s \right) =\frac{1}{s} R(s)=s1
稳态误差Steady State Error——FVT终值定理
e s s = lim t → ∞ e ( t ) = lim s → o s E ( s ) = lim s → o s ⋅ 1 s 1 1 + K N ( s ) D ( s ) = 1 1 + K N ( 0 ) D ( 0 ) = D ( 0 ) D ( 0 ) + K N ( 0 ) ess=\underset{t\rightarrow \infty}{\lim}e\left( t \right) =\underset{s\rightarrow o}{\lim}sE\left( s \right) =\underset{s\rightarrow o}{\lim}s\cdot \frac{1}{s}\frac{1}{1+K\frac{N\left( s \right)}{D\left( s \right)}}=\frac{1}{1+K\frac{N\left( 0 \right)}{D\left( 0 \right)}}=\frac{D\left( 0 \right)}{D\left( 0 \right) +KN\left( 0 \right)} ess=t→∞lime(t)=s→olimsE(s)=s→olims⋅s11+KD(s)N(s)1=1+KD(0)N(0)1=D(0)+KN(0)D(0)


相关文章:

[足式机器人]Part2 Dr. CAN学习笔记-自动控制原理Ch1-8Lag Compensator滞后补偿器
本文仅供学习使用 本文参考: B站:DR_CAN Dr. CAN学习笔记-自动控制原理Ch1-8Lag Compensator滞后补偿器 从稳态误差入手(steady state Error) 误差 Error : E ( s ) R ( s ) − X ( s ) R ( s ) − E ( s ) ⋅ K G …...

swift-碰到的问题
如何让工程不使用storyboard和scene 删除info.plist里面的Application Scene mainifest 删除SceneDelegate.swift 删除AppDelegate.swift里面的这两个方法 func application(_ application: UIApplication, configurationForConnecting connectingSceneSession: UISceneSession…...

安全与认证Week4
目录 目录 Web Security (TLS/SSL) 各层安全协议 Transport Layer Security (TLS)传输层安全性(TLS) SSL和TLS的联系与区别 TLS connection&session 连接与会话 题目2答案点 TLS ArchitectureTLS架构(5个协议) 题目1答案点 Handshake Proto…...

Golang高质量编程与性能调优实战
1.1 简介 高质量:编写的代码能否达到正确可靠、简洁清晰的目标 各种边界条件是否考虑完备异常情况处理,稳定性保证易读易维护编程原则 简单性 消除多余的重复性,以简单清晰的逻辑编写代码不理解的代码无法修复改进可读性 代码是写给人看的,并不是机器编写可维护代码的第一…...

vite 如何打包 dist 文件到 zip 使用插件 vite-plugin-zip-pack,vue3 ts
vite 如何打包 dist 文件到 zip 使用插件 vite-plugin-zip-pack,vue3 ts 开发过程中一个经常做的事就是将 ./dist 文件夹打包成 zip 分发。 每次手动打包还是很费劲的, vite 同样也有能把 ./dist 文件夹打包成 .zip 的插件,当然这个打包的文…...
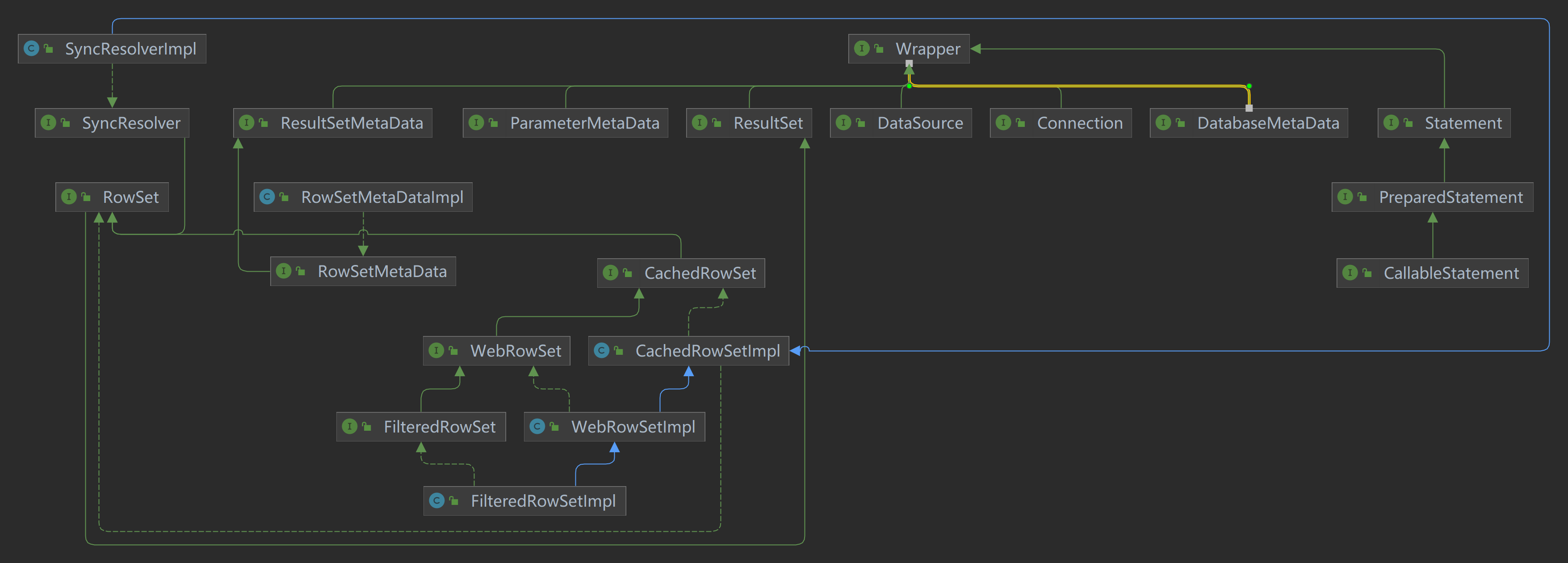
jdbc源码研究
JDBC介绍 JDBC(Java Data Base Connectivity,java数据库连接)是一种用于执行SQL语句的Java API,可以为多种关系数据库提供统一访问,它由一组用Java语言编写的类和接口组成。 开发者不必为每家数据通信协议的不同而疲于奔命&#…...
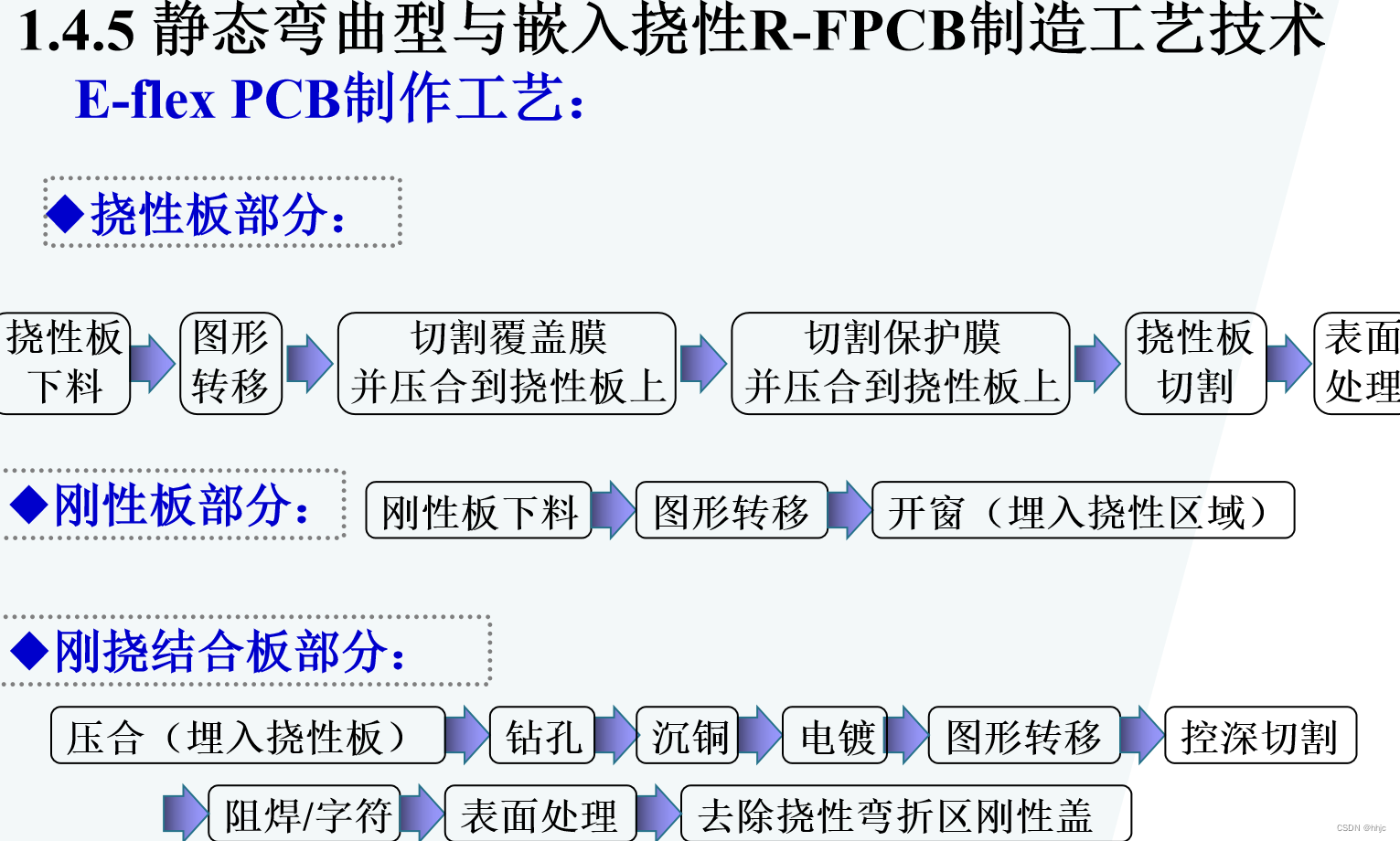
挠性及刚挠结合印制电路技术
1.1挠性印制电路板概述 20世纪70年代末期,以日本厂商为主导,逐渐将挠性印制电路板(flexible printedcircuit board,FPCB,简称为FPC)广泛应用于计算机、照相机、打印机、汽车音响、硬盘驱动器等电子信息产品中。20世纪90年代初期&…...

Python+OpenGL绘制3D模型(七)制作3dsmax导出插件
系列文章 一、逆向工程 Sketchup 逆向工程(一)破解.skp文件数据结构 Sketchup 逆向工程(二)分析三维模型数据结构 Sketchup 逆向工程(三)软件逆向工程从何处入手 Sketchup 逆向工程(四…...

MediaPipeUnityPlugin Win10环境搭建(22年3月的记录,新版本已完全不同,这里只做记录)
https://github.com/homuler/MediaPipeUnityPlugin You cannot build libraries for Android with the following steps. 1、安装msys2配置系统环境变量Path添加 C:\msys64\usr\bin 执行 pacman -Su 执行 pacman -S git patch unzip 2、安装Python3.9.10 勾选系统环境变量 …...

Nginx - location块中的alias和try_files重定向
nginx.conf片段: location /logo/general/ {autoindex_localtime on;alias /opt/config/;try_files /logo/logo.png /www/html/logo.png 404;} 意为:访问/logo/general/地址时, 如:访问http://127.0.0.1/logo/general/logo.png…...
总结Ⅲ)
二刷Laravel 教程(用户模型)总结Ⅲ
一、数据库迁移 当我们运行迁移时,up 方法会被调用;(创建表) 当我们回滚迁移时,down 方法会被调用。(删除表) public function up() { //create 方法会接收两个参数:一个是数据…...
安装PyTorch及环境配置(应用于Python上的YOLO)
这个基本都是Bilibili网站里面叫“小手丫子”up的视频教程,此前自己需要装了好几次又卸载了好几次,现在根据视频教学整理出来自己所理解的文档。 注意事项 1.安装的pycharm版本和anaconda版本无要求。 2.运行pycharm尽量以管理员身份运行。 3.Cuda是独…...

【194】PostgreSQL 14.5 编写SQL从身份证号中查找性别,并且更新性别字段。
假设有一张用户表 t_user ,该表设计如下: id: character varying 主键 name: character varying 姓名 idcard: character varying 身份证号 gender: smallint 性别,女是0,男是1根据身份证号查找所有未填写…...

微服务管家:NestJS 如何使用服务发现 Consul 实现高效的微服务节点管理
前言 在微服务架构中,服务发现是一项基础且关键的功能,它允许服务实例在网络中被动态发现。Consul 是一种服务网格解决方案,提供了服务发现、运行状况检查,过去和现代应用程序的连接等功能。 本教程将向您展示如何在 NestJS 框架…...

Baumer工业相机堡盟工业相机如何联合NEOAPI SDK和OpenCV实现相机图像转换为Mat图像格式(C++)
Baumer工业相机堡盟工业相机如何通过NEOAPI SDK实现相机掉线自动重连(C) Baumer工业相机Baumer工业相机的图像转换为OpenCV的Mat图像的技术背景在NEOAPI SDK里实现相机图像转换为Mat图像格式联合OpenCV实现相机图像转换为Mat图像格式测试演示图 工业相机…...

铁塔基站数字化管理监测解决方案
截至2023年10月,我国5G基站总数达321.5万个,占全国通信基站总数的28.1%。然而,随着5G基站数量的快速增长,基站的能耗问题也逐渐日益凸显,基站的用电给运营商带来了巨大的电费开支压力,降低5G基站的能耗成为…...
)
如何使用Python3 Boto3删除AWS CloudFormation的栈(Stacks)
文章目录 小结问题及解决有关Json文件的输入和输出使用Python3及正则表达式查找字符串包含某个子字符串使用Python3 Boto3删除AWS CloudFormation的栈(Stacks) 参考 小结 本文记录了使用Python3的Boto3包删除AWS CloudFormation的栈(Stacks&…...
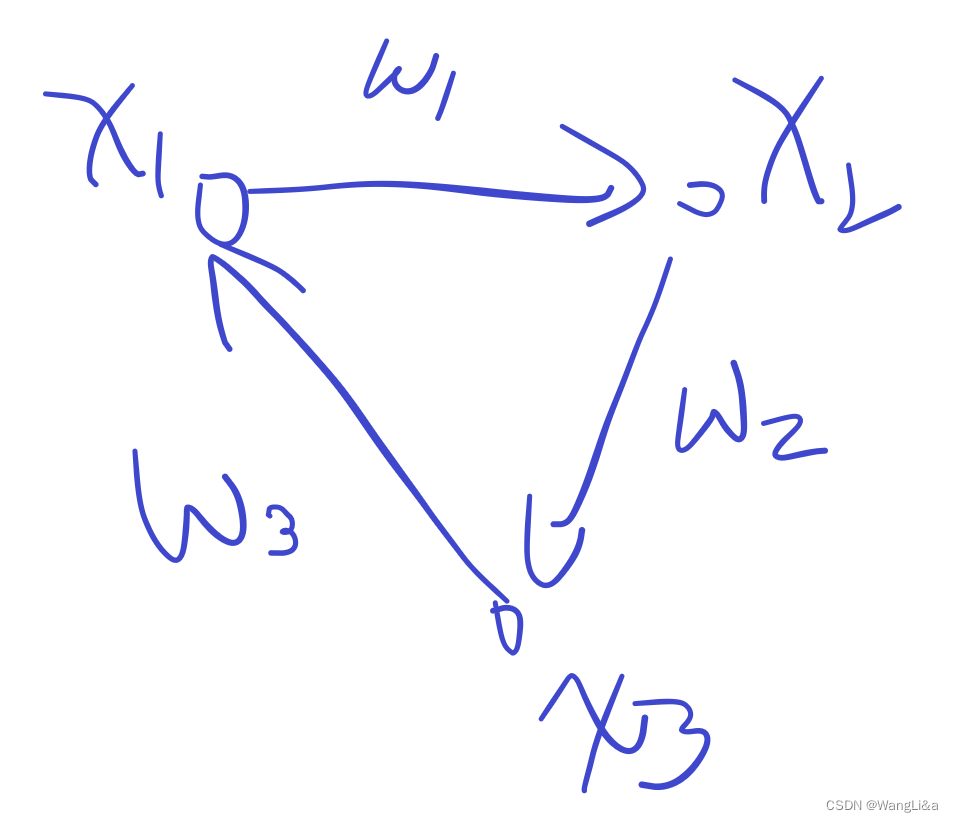
差分约束算法
差分约束 差分约束系统包含 m m m个涉及 n n n个变量的差额限制条件,这些差额限制条件每个都是形式为 x i − x j ≤ b ∈ [ 1 , m ] x_i-x_j\leq b_{\in[1,m]} xi−xj≤b∈[1,m]的简单线性不等式。 通常我们要求解出一组可行解。 最短路差分约束 如果我们…...
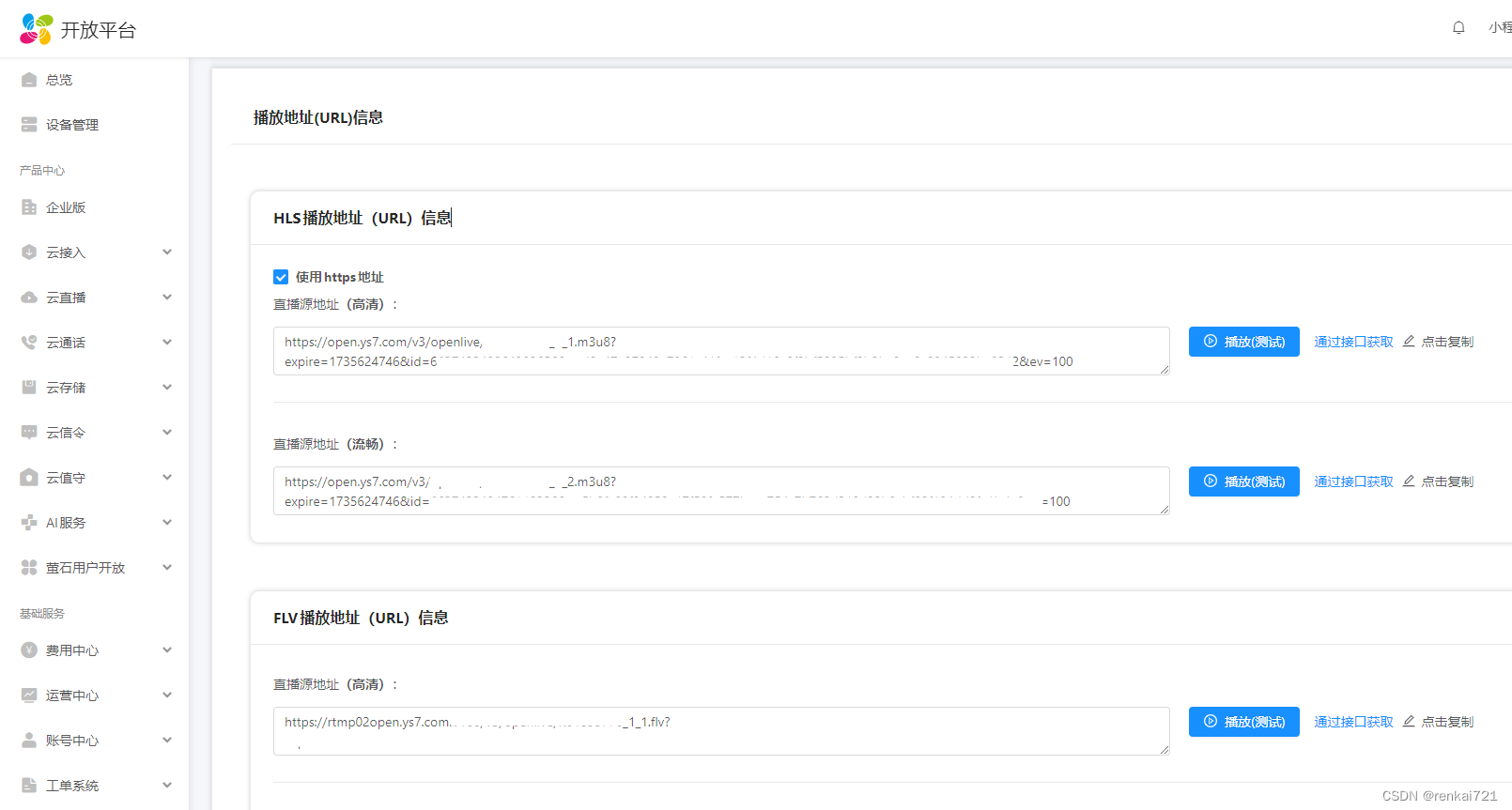
彻底解决vue-video-player播放视频有黑边
需求 最近需要接入海康视频摄像头,然后把视频的画面接入到自己的网站系统中。以前对接过rtsp固定IP的显示视频,这次的不一样,没有了固定IP。海康的解决办法是,摄像头通过配置服务器到萤石云平台,然后购买企业版账号和…...

区域负责人常用的ChatGPT通用提示词模板
区域市场分析:如何分析区域市场的特点、竞争态势和客户需求? 区域销售策略制定:如何制定针对区域市场的销售策略,包括产品定位、价格策略、渠道策略等? 区域销售目标设定:如何设定明确的区域销售目标&…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...
