开始刷Leetcode之前你需要知道的 - The basic is all you need
数据结构:列表,哈希表,集合,栈,堆,链表,二叉树,图
入门算法:递归,排序算法,二分法,bfs,dfs
list/array
列表常见操作,以及相关的时间复杂度。
append 一个元素、pop 末尾元素均为 O(1)
查找某个元素的索引 O(n)
new_list = []
# add
new_list.append(1) # add 1 to the end of list, O(1)
new_list.insert(0, 3) # add 3 to the beginning of list, O(n)# remove
list1 = [1, 2, 3, 2, 3, 4, 5, 6]
list1.pop() # remove the last element of list, O(1)
list1.pop(0) # remove the first element of list, O(n)
list1.remove(2) # remove the first match element in the list# access
new_list[1] # output: 1, access by index # O(1)
# list1: [2, 3, 2, 3, 4, 5]
list1[start:end] # the length of slice is k, O(k)
# list1[1:4] is [3, 2, 3]# search
res = 2 in list1 # O(n)
res # true# get the length of list
len(list1) # O(1)# sort
list1.sort() # O(nlogn)# reverse the list
list1.reverse() # O(n)# check if is empty
not list1 # False
hash
什么是哈希,哈希函数是什么,最常见的哈希表数据结构是什么(集合与哈希表)?
什么是哈希
哈希(Hashing)是一种将输入(或者称为“键”)转换成固定大小的值的过程,这个值通常是一个整数,被称为哈希值。哈希的目的主要是为了实现快速的数据查找和存取,因为通过哈希值(通常是一个较小的索引)来访问数据要比通过其他方式(比如遍历)快得多。
哈希函数是什么
哈希函数是实现哈希的具体方法,它接受输入,并返回一个通常是固定大小的数值(哈希值)。好的哈希函数应具备以下特性:
快速计算:能够快速地计算出任意输入的哈希值。
哈希值均匀分布:对于不同的输入,哈希值应该均匀地分布在所有可能的哈希值中,以减少碰撞(不同的输入得到相同的哈希值)。
碰撞最小化:尽管理论上任何哈希函数都会有碰撞,好的哈希函数会尽可能地减少碰撞的概率。
哈希表(Hash Table):是一种实现了映射(键与值的对应关系)的数据结构,它使用哈希函数将键转换为数组的索引,这个索引决定了值的存放位置。因为这个转换过程几乎是即时的,哈希表在平均情况下为各种操作提供了快速的时间复杂度。
集合(Set):特别的哈希表,它仅存储键,不存储值。集合通常用于快速地检查一个元素是否存在于集合中。
Hashmap/ dict/ unordered_map
哈希表一般用于干什么?
哈希表有哪些常见操作?对应的时间复杂度,空间复杂度分别是什么?
哈希表的实现:字典(Dictionary)
在Python中字典是基于哈希表实现的
my_dict = {}
# add
my_dict["apple"] = "A fruit"
my_dict["python"] = "A programming language"
my_dict # {'apple': 'A fruit', 'python': 'A programming language'}# remove
del my_dict["apple"]# search
if "python" in my_dict:print(my_dict["python"] # A programming language
set/ hashset
对于集合,操作和时间复杂度类似,因为它通常就是一个没有“值”的哈希表。
集合一般用于干什么?
集合的常见操作有哪些?每个常见操作的时间复杂度是什么?
my_set = set()# add
my_set.add(1)
my_set.add(2)
my_set.add(3)
my_set # {1, 2, 3}
# remove
my_set.remove(2) # 如果元素不存在,remove会引发错误
# 或者使用discard,不会引发错误
my_set.discard(3) # 如果元素不存在,什么也不会发生
my_set # {1}# check existance
1 in my_set # True
stack
什么是栈?什么是后进先出?
栈一般用于解决什么问题?
什么是程序栈?
你所熟悉的语言当中栈是用什么数据结构实现的?(在Python中,栈通常使用列表(List)数据结构来实现)
栈一般用于解决什么问题?
函数调用:在任何现代编程语言中,函数调用的实现都是使用栈来完成的,这个栈被称为调用栈或程序栈。
括号匹配问题:例如,编译器在编译时用栈来处理括号匹配。
撤销操作:许多应用程序使用栈来跟踪用户的操作,以便用户可以撤销它们。
表达式求值:栈可以用来对后缀表达式进行求值,以及将中缀表达式转换为后缀表达式。
程序栈,也称为调用栈,是一种特殊类型的栈,用于存储活跃的子程序的信息。这包括局部变量、返回地址、参数等。当一个函数被调用时,它的上下文被推入程序栈,当函数返回时,它的上下文被弹出。
一个栈示例:
Push (元素入栈): O(1)
Pop (元素出栈): O(1)
Peek (获取栈顶元素,但不弹出): O(1)
IsEmpty (检查栈是否为空): O(1)
class Stack:def __init__(self):self.items = []def is_empty(self):return not self.itemsdef push(self, item):self.items.append(item)def pop(self):if not self.is_empty():return self.items.pop()raise IndexError("Pop from empty stack")def peek(self):if not self.is_empty():return self.items[-1]raise IndexError("Peek from empty stack")def size(self):return len(self.items)# 使用栈
my_stack = Stack()
my_stack.push(1)
my_stack.push(2)
my_stack.push(3)print(my_stack.pop()) # 输出 3
print(my_stack.peek()) # 输出 2
print(my_stack.is_empty()) # 输出 False
queue
什么是队列?什么是先进先出?
队列一般应用在哪些场景当中?
什么是消息队列?
你所熟悉的语言当中栈是用什么数据结构实现的?(Python 当中可以用 deque 或者 queue)
队列一般应用在哪些场景当中?
操作系统的任务调度:操作系统使用队列来管理多个进程的执行。
打印队列管理:在办公环境中,打印任务被添加到队列中,并按顺序执行。
实时系统的请求处理:如银行或票务系统,客户的请求按照到达的顺序处理。
网络中的数据包传输:数据包按顺序发送和接收。
什么是消息队列?
消息队列是一种应用程序间通信方法,应用程序通过读写出入队列的消息来通信,从而实现异步处理。消息队列提供了一种跨进程通信机制,用于在不同的进程中传递消息或数据。这种结构广泛应用于服务器和客户端之间的通信,以及在微服务架构中各服务间的消息传递。
Python中队列的实现
在Python中,队列通常使用collections.deque或者queue.Queue来实现。
常见操作及其时间复杂度:
Enqueue (元素入队): O(1)
Dequeue (元素出队): O(1)
IsEmpty (检查队列是否为空): O(1)
Peek/Front (查看队列的头部元素): O(1)
from collections import dequeclass Queue:def __init__(self):self.items = deque()def is_empty(self):return not self.itemsdef enqueue(self, item):self.items.append(item)def dequeue(self):if not self.is_empty():return self.items.popleft()raise IndexError("Dequeue from empty queue")def front(self):if not self.is_empty():return self.items[0]raise IndexError("Front from empty queue")def size(self):return len(self.items)# 使用队列
my_queue = Queue()
my_queue.enqueue(1)
my_queue.enqueue(2)
my_queue.enqueue(3)print(my_queue.dequeue()) # 输出 1
print(my_queue.front()) # 输出 2
print(my_queue.is_empty()) # 输出 Falseheap
什么是堆?什么是最大堆、最小堆?
堆一般用于解决什么问题?
你所熟悉的语言当中堆是用什么数据结构实现的?(Python 当中堆用的是列表实现的,并且 Python 只有最小堆没有最大堆)
一般语言不自带的数据结构:(需要自己手工创建)
什么是堆?
堆(Heap)是一种特殊的完全二叉树。所有的节点都大于等于(最大堆)或小于等于(最小堆)它们的子节点。堆常常被用作优先队列,因为它允许快速访问到最大值或最小值。
什么是最大堆、最小堆?
最大堆:在最大堆中,任何一个父节点的值都大于或等于它的子节点的值。根节点是最大的值,即堆顶是所有节点中最大的节点。
最小堆:在最小堆中,任何一个父节点的值都小于或等于它的子节点的值。根节点是最小的值,即堆顶是所有节点中最小的节点。
堆一般用于解决什么问题?
优先队列:堆是实现优先队列的常用数据结构,用于管理一组有优先级的对象。
堆排序:利用堆可以高效地进行排序,称为堆排序。
选择问题:如找出一组数中的最大k个数或最小k个数。
Python中堆的实现
在Python中,堆通常使用列表实现,并通过标准库heapq提供的函数来操作这些列表作为堆。注意,Python的heapq模块提供的是最小堆的实现。
常见操作及其时间复杂度
插入(heapq.heappush): O(log n) - 向堆中添加一个新元素。
删除最小值(heapq.heappop): O(log n) - 从堆中弹出最小元素。
查找最小值: O(1) - 查看堆顶元素(最小值)。
创建堆(heapq.heapify): O(n) - 将一个列表转换成堆结构。
用Python实现堆的操作示例
import heapq# 创建一个空堆
heap = []# 插入元素
heapq.heappush(heap, 10)
heapq.heappush(heap, 1)
heapq.heappush(heap, 5)# 查看最小值,但不删除
print(heap[0])# 删除并返回最小值
print(heapq.heappop(heap))# 将列表转换为堆
list_for_heap = [3, 1, 4, 1, 5, 9, 2, 6, 5]
heapq.heapify(list_for_heap)
print(list_for_heap) # [1, 1, 2, 3, 5, 9, 4, 6, 5]
linked list
链表的节点(node)是如何实现的?
如何创建一个链表?
如何遍历一个链表?
如何在链表中查找一个元素是否存在?
如何在链表中添加/删除一个元素?
链表节点的实现
链表的节点通常包含两个部分:一个是存储的数据,另一个是指向下一个节点的引用(在双向链表中可能还包含指向前一个节点的引用)。在Python中,节点通常通过创建一个类来实现。
如何创建一个链表?
创建一个链表通常包括两个步骤:定义节点类,然后创建节点并将它们链接起来形成链表。
如何遍历一个链表?
遍历链表通常使用一个循环,从头节点开始,访问每个节点直到到达链表尾部的None指针。
如何在链表中查找一个元素是否存在?
查找一个元素通常需要遍历链表,比较每个节点的数据域,直到找到相应的元素或者遍历完整个链表。
如何在链表中添加/删除一个元素?
添加元素可以有多种方式,常见的有在链表头部添加(头插法),在链表尾部添加(尾插法),或者在指定节点后添加。
删除元素通常涉及到找到该元素所在的节点,然后更改前一个节点的指针来排除该节点。
常见操作及其时间复杂度
遍历: O(n) - 需要遍历每个节点。
搜索: O(n) - 最坏情况下需要遍历每个节点。
插入: O(1) - 如果知道目标位置,插入操作本身是常数时间,但如果需要在特定位置插入,可能需要O(n)时间找到位置。
删除: O(1) - 如果知道目标节点,删除操作本身是常数时间,但通常需要O(n)时间来找到要删除的节点。
用Python实现链表的操作示例
下面是如何在Python中实现简单的单向链表及其基本操作:
class ListNode:def __init__(self, data):self.data = dataself.next = Noneclass LinkedList:def __init__(self):self.head = Nonedef append(self, data):if not self.head:self.head = ListNode(data)else:current = self.headwhile current.next:current = current.nextcurrent.next = ListNode(data)def find(self, key):current = self.headwhile current:if current.data == key:return Truecurrent = current.nextreturn Falsedef delete(self, key):current = self.headprevious = Nonewhile current and current.data != key:previous = currentcurrent = current.nextif previous is None:self.head = current.nextelif current:previous.next = current.nextcurrent.next = Nonedef display(self):current = self.headwhile current:print(current.data, end=" -> ")current = current.nextprint("None")# 使用链表
ll = LinkedList()
ll.append(1)
ll.append(2)
ll.append(3)ll.display() # 打印链表
print("2 is in the list:", ll.find(2)) # 查找元素
ll.delete(2) # 删除元素
ll.display() # 再次打印链表
以上代码演示了如何实现一个简单的单向链表,以及如何进行插入、查找和删除操作。链表的每个节点是通过ListNode类实现的,而链表的操作则是通过LinkedList类进行管理。
binary tree
二叉树的节点(node)是如何实现的?
如何创建一个二叉树?
如何遍历一个链表?何谓二叉树的层序、前序、中序、后序遍历?
二叉搜索树(二叉查找树、binary search tree、BST)
与普通的二叉树相比,二叉搜索树特点是什么?如何证明一棵二叉树是/不是一课二叉搜索树?
一个二叉树是二叉搜索树 <-> 该二叉树的中序遍历是单调递增的
二叉树的节点实现
二叉树的节点通常包含三个部分:一个是存储的数据,另外两个是指向左子节点和右子节点的引用。在Python中,节点通常通过创建一个类来实现。
创建二叉树
创建一个二叉树通常包括定义节点类,并通过连接这些节点来形成树结构。
二叉树的遍历
遍历二叉树是指按照某种顺序访问树中的每个节点一次且仅一次。
- 层序遍历:按照树的层次从上到下访问每个节点。
- 前序遍历:先访问根节点,然后遍历左子树,最后遍历右子树。
- 中序遍历:先遍历左子树,然后访问根节点,最后遍历右子树。
- 后序遍历:先遍历左子树,然后遍历右子树,最后访问根节点。
二叉搜索树(BST)
二叉搜索树(Binary Search Tree,BST)是一种特殊的二叉树,它具有以下特性:
- 每个节点的值都大于其左子树上任意节点的值。
- 每个节点的值都小于其右子树上任意节点的值。
- 左右子树也分别是二叉搜索树。
如何证明一棵树是二叉搜索树
一个二叉树是二叉搜索树当且仅当其中序遍历的结果是单调递增的。这是因为在中序遍历中,左子树(较小的值)先被访问,接着是根节点,然后是右子树(较大的值)。
常见操作及其时间复杂度
- 搜索: O(h) - h为树的高度。
- 插入: O(h) - 插入新节点。
- 删除: O(h) - 删除存在的节点。
- 最大/最小值查找: O(h) - 查找最大或最小值节点。
用Python实现BST的操作示例
class TreeNode:def __init__(self, value):self.value = valueself.left = Noneself.right = Noneclass BinarySearchTree:def __init__(self):self.root = Nonedef insert(self, value):if not self.root:self.root = TreeNode(value)else:self._insert_recursive(self.root, value)def _insert_recursive(self, node, value):if value < node.value:if node.left is None:node.left = TreeNode(value)else:self._insert_recursive(node.left, value)elif value > node.value:if node.right is None:node.right = TreeNode(value)else:self._insert_recursive(node.right, value)def inorder_traversal(self, node, result=None):if result is None:result = []if node:self.inorder_traversal(node.left, result)result.append(node.value)self.inorder_traversal(node.right, result)return result# 使用BST
bst = BinarySearchTree()
bst.insert(3)
bst.insert(1)
bst.insert(4)
bst.insert(2)# 中序遍历BST
print(bst.inorder_traversal(bst.root)) # 输出应为[1, 2, 3, 4],一个单调递增序列
以上代码演示了如何在Python中实现一个基本的二叉搜索树,包括插入节点和中序遍历。中序遍历的结果是单调递增的,这也验证了二叉搜索树的性质。
graph
什么是图?什么是有向图(directed graph)?什么是无向图(undirected graph)?
图与树的关系是?如何知道一个图是不是一课树?
如何实现一个简单图?
什么是图?
图(Graph)是由节点(或称为顶点,vertices)以及连接这些顶点的边(edges)组成的结构。它可以用来表示任何二元关系,如网络模型、路径寻找、社交网络等。
有向图与无向图
- 有向图(Directed Graph):图中的边有方向,表示从一个顶点指向另一个顶点。用箭头表示边的方向。
- 无向图(Undirected Graph):图中的边没有方向,表示两个顶点互相连接。通常用一条普通的线表示边。
图与树的关系
树是一种特殊的图。具体来说:
- 树(Tree):是一个无环连通的无向图,也就是说,任意两个顶点之间有且仅有一条路径,且没有回路。
- 图(Graph):可以有环,可以不连通,边可以有方向(有向图)或没有方向(无向图)。
如何知道一个图是不是一棵树?
一个图是树的充分必要条件是:
- 无环:图中没有环。
- 连通:图中任意两个顶点都是连通的。
- 边数:对于n个顶点的图,恰好有n-1条边。
实现一个简单的图
图通常可以通过邻接矩阵或邻接列表来实现。邻接列表是一种空间效率更高的实现方式,尤其是对于稀疏图而言。
常见操作及其时间复杂度
- 添加顶点: O(1) - 添加一个顶点。
- 添加边: O(1) - 在邻接列表中,添加一条边。
- 搜索顶点: O(V) - 在顶点列表中搜索顶点。
- 搜索边: O(V) - 在邻接列表中搜索边。
用Python实现图的操作示例
以下是使用邻接列表来实现一个无向图的示例:
class Graph:def __init__(self):self.adj_list = {} # 邻接列表def add_vertex(self, vertex):if vertex not in self.adj_list:self.adj_list[vertex] = []def add_edge(self, v1, v2):if v1 in self.adj_list and v2 in self.adj_list:self.adj_list[v1].append(v2) # 添加边v1->v2self.adj_list[v2].append(v1) # 对于无向图,同时添加边v2->v1def display(self):for vertex in self.adj_list:print(f"{vertex}: {self.adj_list[vertex]}")# 创建图实例
graph = Graph()# 添加顶点
graph.add_vertex('A')
graph.add_vertex('B')
graph.add_vertex('C')# 添加边
graph.add_edge('A', 'B')
graph.add_edge('B', 'C')# 显示图
graph.display()
这段代码展示了如何创建顶点和边,并将它们添加到图中。display() 方法用于打印图的邻接列表,展示了图的结构。这个简单的例子实现的是无向图,有向图的实现只需在add_edge时不添加反向边即可。
应该掌握的入门算法:
递归:
什么是递归?
递归的优势、劣势是什么?
递归三要素是什么?
排序算法:
快速排序如何实现?时间/空间复杂度是多少?
归并排序如何实现?时间/空间复杂度是多少?
二分法:
二分法的基本原理是什么?
二分法一般用于解决什么问题?
二分法的时间复杂度是什么?
宽度优先遍历(宽度优先搜索、Breadth first search、BFS):
宽度优先遍历的模板是什么?
宽度优先遍历的时间/空间复杂度是什么?
宽度优先遍历一颗二叉树与一个图的区别在哪?
宽度优先遍历一般用于解决什么问题?
深度优先遍历(深度优先搜索、Depth first search、DFS):
深度优先遍历的模板是什么?
深度优先遍历的时间/空间复杂度是什么?
深度优先遍历一颗二叉树与一个图的区别在哪?
深度优先遍历一般用于解决什么问题?
相关文章:

开始刷Leetcode之前你需要知道的 - The basic is all you need
数据结构:列表,哈希表,集合,栈,堆,链表,二叉树,图 入门算法:递归,排序算法,二分法,bfs,dfs list/array 列表常见操作&am…...

【PostgreSQL】模式Schema
PostgreSQL 数据库集群包含一个或多个命名数据库。角色和一些其他对象类型在整个集群中共享。与服务器的客户端连接只能访问单个数据库中的数据,该数据库在连接请求中指定。 数据库包含一个或多个命名schema,而这些schema又包含表。schema还包含其他类型…...

JavaScript实现的复杂功能:自动生成带水印的图片
#程序员的崩溃瞬间 在本文中,我们将讨论一个JavaScript实现的复杂功能,该功能可以自动为图片添加水印。这个功能在许多场景中都非常有用,例如,如果你想保护你的图片版权,或者你想在你的网站上显示自定义的水印。 一、…...
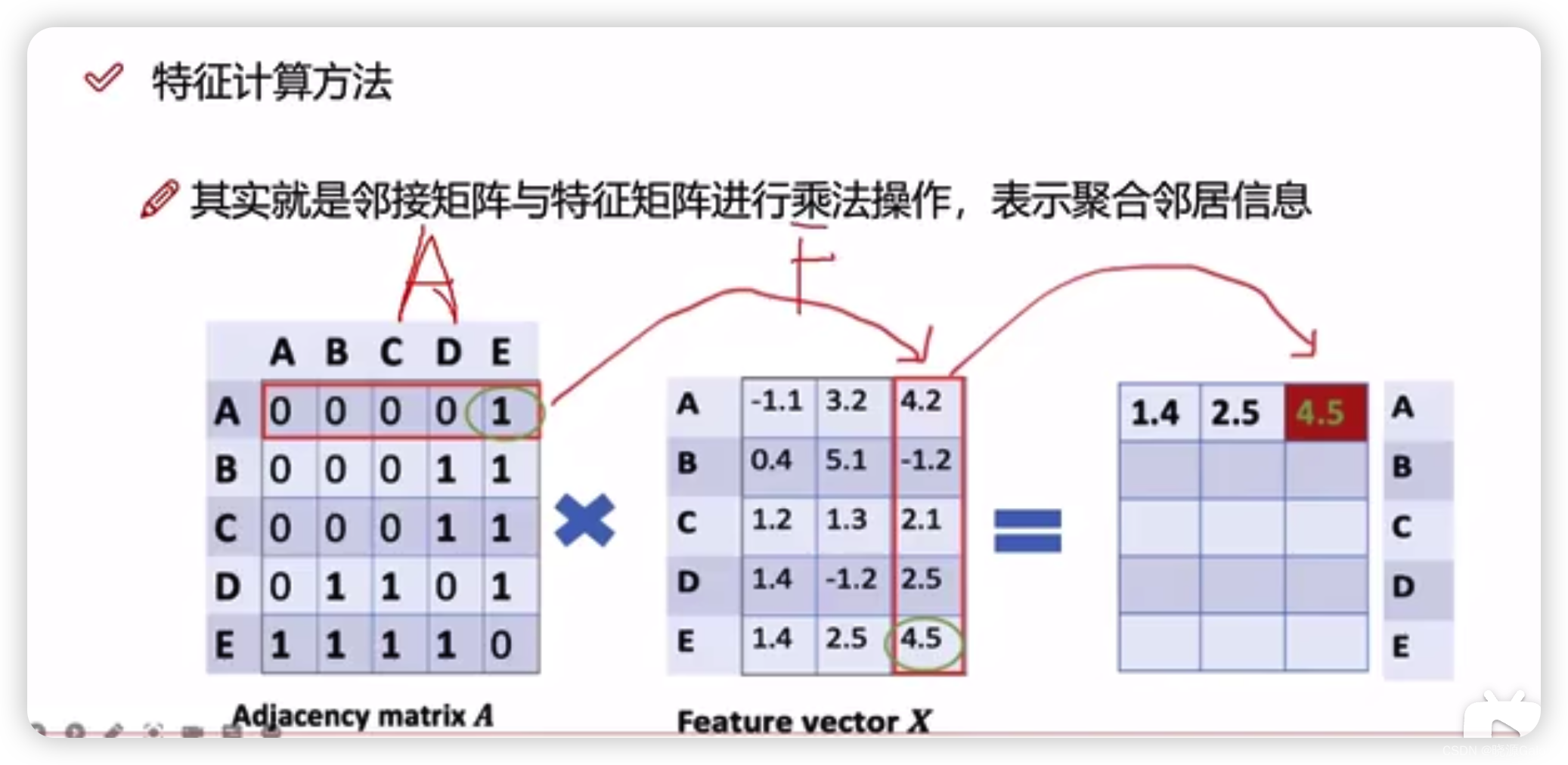
图神经网络|8.2 图卷积的计算基本方法
不同于一般的神经网络,网络层数的并不用特别多。 原因是只需要少数次数迭代后(当迭代次数为图上的直径?任意两点最短距离的最大值?),某节点便可获取得到图上所有的节点。 通俗的理解是,在社会中…...

equals()与hashCode()方法详解
java.lang.Object类中有两个非常重要的方法: 1 2 public boolean equals(Object obj) public int hashCode() Object类是类继承结构的基础,所以是每一个类的父类。所有的对象,包括数组,都实现了在Object类中定义的方法。 回到…...

六、基于Flask、Flasgger、marshmallow的开发调试
基于Flask、Flasgger、marshmallow的开发调试 问题描述调试方法一调试方法二调试方法三 问题描述 现在有一个传入传出为json格式文件的,Flask-restful开发的程序,需要解决如何调试的问题。 #!/usr/bin/python3 # -*- coding: utf-8 -*- # Project :…...

TypeScript 从入门到进阶之基础篇(三) 元组类型篇
系列文章目录 TypeScript 从入门到进阶系列 TypeScript 从入门到进阶之基础篇(一) ts基础类型篇TypeScript 从入门到进阶之基础篇(二) ts进阶类型篇TypeScript 从入门到进阶之基础篇(三) 元组类型篇TypeScript 从入门到进阶之基础篇(四) symbol类型篇 持续更新中… 文章目录 …...

现代CPU的多种运行模式
目前的CPU大多是支持X86-64技术的兼容CPU,这包括AMD64以及Intel的IA32E(后被正式命名为EM64T,Extended Memory 64 Technology),因为AMD64先出,而EM64T与AMD64完全兼容,所以也统一称为AMD64技术。…...

Python PDF处理模块pypdf库详解
概要 PDF(Portable Document Format)是一种常见的文档格式,广泛用于存储和共享文本和图像数据。在 Python 中,有许多库可以用于处理 PDF 文件,其中之一就是 PyPDF。PyPDF 是一个功能强大的库,它允许你读取…...

C++上位软件通过LibModbus开源库和西门子S7-1200/S7-1500/S7-200 PLC进行ModbusTcp 和ModbusRTU 通信
前言 一直以来上位软件比如C等和西门子等其他品牌PLC之间的数据交换都是大家比较头疼的问题,尤其是C上位软件程序员。传统的方法一般有OPC、Socket 等,直到LibModbus 开源库出现后这种途径对程序袁来说又有了新的选择。 Modbus简介 Modbus特点 1 &#…...
PLSQL Developer 15安装和oracle客户端安装
文章目录 前言一、PLSQL Developer1.下载2.安装 二、oracle客户端1.下载2.环境变量 三、使用1. oci2. 连接3. 配置文件 总结 前言 oracle是经常使用的数据库,PLSQL Developer是众多产品中比较不错的一款工具,接下来我们来介绍PLSQL Developer的安装和使…...
【深度deepin】深度安装,jdk,tomcat,Nginx安装
目录 一 深度 1.1 介绍 1.2 与别的操作系统的优点 二 下载镜像文件及VM安装deepin 三 jdk,tomcat,Nginx安装 3.1 JDK安装 3.2 安装tomcat 3.3 安装nginx 一 深度 1.1 介绍 由深度科技社区开发的开源操作系统,基于Linux内核…...
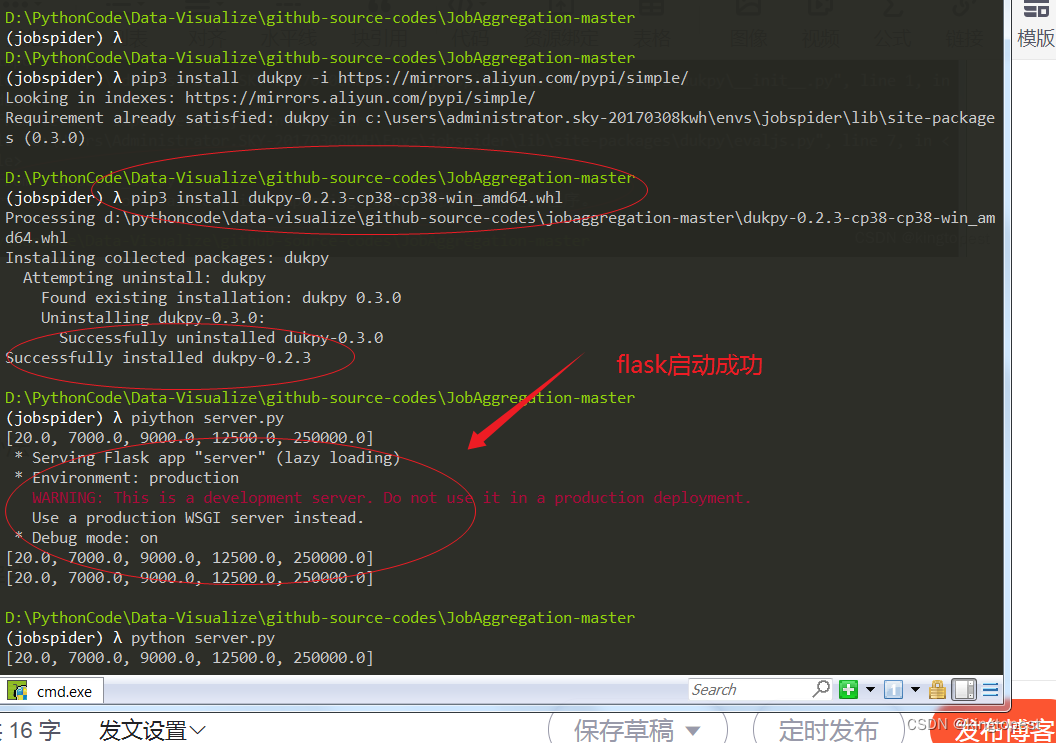
解决flask启动报错:ImportError: DLL load failed while importing _dukpy: 找不到指定的程序
现象: 原因:dukpy没有win32执行库 解决办法: 到lfd.uci.edu 第三方库下载dukpy的win32 whl文件 注意: 需要跟你python版本和windows平台(32位/64位)对应 https://www.lfd.uci.edu/~gohlke/pythonlibs/#…...
腾讯面试总结
腾讯 一面 mysql索引结构?redis持久化策略?zookeeper节点类型说一下;zookeeper选举机制?zookeeper主节点故障,如何重新选举?syn机制?线程池的核心参数;threadlocal的实现ÿ…...
面向对象进阶(static关键字,继承,方法重写,super,this)
文章目录 面向对象进阶部分学习方法:今日内容教学目标 第一章 复习回顾1.1 如何定义类1.2 如何通过类创建对象1.3 封装1.3.1 封装的步骤1.3.2 封装的步骤实现 1.4 构造方法1.4.1 构造方法的作用1.4.2 构造方法的格式1.4.3 构造方法的应用 1.5 this关键字的作用1.5.1…...

Blazor项目如何调用js文件
以下是来自千问的回答并加以整理:(说一句,文心3.5所给的回答不完善,根本运行不起来,4.0等有钱了试试) 在Blazor项目中引用JavaScript文件(.js)以实现与JavaScript的互操作ÿ…...
Windows11 - Ubuntu 双系统及 ROS、ROS2 安装
系列文章目录 前言 一、Windows11 - Ubuntu 双系统安装 硬件信息: 设备名称 DESKTOP-B62D6KE 处理器 13th Gen Intel(R) Core(TM) i5-13500H 2.60 GHz 机带 RAM 40.0 GB (39.8 GB 可用) 设备 ID 7673EF86-8370-41D0-8831-84926668C05A 产品 ID 00331-10000-0000…...

深度学习(学习记录)
题型:填空题判断题30分、简答题20分、计算题20分、综合题(30分) 综合题(解决实际工程问题,不考实验、不考代码、考思想) 一、深度学习绪论(非重点不做考察) 1、传统机器学习&…...

html5实现好看的个人博客模板源码
文章目录 1.设计来源1.1 主界面1.2 认识我界面1.3 我的文章界面1.4 我的模板界面1.5 文章内容界面 2.结构和源码2.1 目录结构2.2 源代码 源码下载 作者:xcLeigh 文章地址:https://blog.csdn.net/weixin_43151418/article/details/135368653 html5实现好看…...
SpringSecurity深度学习
SpringSecurity简介 spring Security是什么? Spring Security 是一个强大且高度可定制的身份验证和访问控制框架,用于保护基于Spring的应用程序。它是Spring项目的一部分,旨在为企业级系统提供全面的安全性解决方案。 一个简单的授权和校验…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

Matlab实现任意伪彩色图像可视化显示
Matlab实现任意伪彩色图像可视化显示 1、灰度原始图像2、RGB彩色原始图像 在科研研究中,如何展示好看的实验结果图像非常重要!!! 1、灰度原始图像 灰度图像每个像素点只有一个数值,代表该点的亮度(或…...

深入浅出WebGL:在浏览器中解锁3D世界的魔法钥匙
WebGL:在浏览器中解锁3D世界的魔法钥匙 引言:网页的边界正在消失 在数字化浪潮的推动下,网页早已不再是静态信息的展示窗口。如今,我们可以在浏览器中体验逼真的3D游戏、交互式数据可视化、虚拟实验室,甚至沉浸式的V…...

渗透实战PortSwigger Labs指南:自定义标签XSS和SVG XSS利用
阻止除自定义标签之外的所有标签 先输入一些标签测试,说是全部标签都被禁了 除了自定义的 自定义<my-tag onmouseoveralert(xss)> <my-tag idx onfocusalert(document.cookie) tabindex1> onfocus 当元素获得焦点时(如通过点击或键盘导航&…...
