Scikit-Learn线性回归(五)
Scikit-Learn线性回归五:岭回归与Lasso回归
- 1、误差与模型复杂度
- 2、范数与正则化
- 2.1、范数
- 2.2、正则化
- 3、Scikit-Learn Ridge回归(岭回归)
- 4、Scikit-Learn Lasso回归
1、误差与模型复杂度
在第二篇文章 Scikit-Learn线性回归(二) 中,我们已经给出了过拟合与模型泛化的概念并使用案例进行了验证
在机器学习中,我们通常会将数据划分为两部分:一部分用来构建模型,然后另一部分用来检验模型的效果。构建模型所用的数据集称为训练集,而验证模型的数据集称为测试集。模型在训练集上的误差称为训练误差(或经验误差);在测试集上的误差称为泛化误差(Generalization Error)
机器学习的目的是探索隐含在数据背后的规律,对具有同一规律的学习集以外的数据,经过训练的模型也能给出合适的输出,该能力称为泛化能力
泛化误差反映了模型对未知数据的预测能力(泛化能力),而我们采用最多的也就是通过泛化误差来评价模型的泛化能力。泛化误差刻画了模型算法的经验风险与期望风险之间的偏差和收敛速度
过拟合是指模型在训练集中表现良好,而在测试集中表现很差,即泛化误差大于经验误差,说明拟合过度,模型泛化能力降低,只能够适用于训练集,通用性不强;欠拟合则指的是模型在训练集中的表现就很差,即经验误差很大

如图所示,图一表示过拟合,可以看到拟合曲线完美的经过了每一个点,模型非常复杂,这种情况下,经验误差极小,但是预测值的方差(误差平方和)会很大。图二表示欠拟合,此时模型过于简单,在训练集上的误差就很大。图三则表示一个理想的拟合模型
欠拟合出现的原因是模型复杂度太低。可能是回归模型自变量(特征)较少或模型不合适。针对欠拟合,解决方案是增大模型复杂度,可以增加自变量(特征)或改变模型。例如,将一阶多元回归模型升级为多项式回归模型
过拟合出现的原因则是模型复杂度太高或训练集太少。可能是自变量(特征)过多或训练集数据量太少等。针对过拟合,除了增加训练集数据量外,还有多种优化算法可以处理。例如,正则化
一般情况下,误差与模型复杂度之间存在如下关系:

如上图所示,横坐标表示模型的复杂度,纵坐标表示模型的误差。其中,偏差(误差)表示真实值与预测值之间的差值;方差表示回归系数的方差,即误差平方(损失函数或误差平方和为所有样本的偏差平方之和)
泛化误差可以分解为三个部分:偏差(Bias)、方差(Variance)和噪声(Noise)。在评估学习模型性能的过程中,我们主要关注偏差与方差,因为噪声属于不可约减的误差(Irreducible Error)
泛化误差 = 偏差 + 方差 + 噪声 泛化误差=偏差 + 方差 + 噪声 泛化误差=偏差+方差+噪声
偏差表示学习模型的期望预测与测试集标签的偏离程度,即刻画了学习模型本身的拟合能力。训练模型越复杂,则偏差越小,例如,线性回归可以通过增加参数个数来提高模型的复杂度,神经网络可以通过增加隐单元个数来提高模型的复杂度
方差表示同样大小的训练数据集的变动所导致的学习性能的变化,即刻画了数据扰动所造成的影响。若模型处于过拟合状态,不同训练数据集产生的学习模型相差较大
噪声表示任何学习模型所能达到期望泛化误差的下界,即刻画了学习问题本身的难度。若噪声比较大,即使是最优模型,泛化误差也比较大
从图中可得,随着模型复杂度的提升,方差会不断增大,偏差会逐渐减小,而泛化误差会受偏差和方差的影响,我们的目标是找到泛化误差的最小值,这可以通过平衡偏差与方差来实现
2、范数与正则化
2.1、范数
范数(Norm)的概念来源于泛函分析与测度理论。其中的定义相当简单明了:范数是具有长度概念的函数,用于衡量一个矢量的大小(测量矢量的测度)
范数是一种距离强化概念,范数通常被用来度量某个向量空间 ∣ ∣ x ∣ ∣ ||x|| ∣∣x∣∣(或矩阵 ∣ ∣ X ∣ ∣ ||X|| ∣∣X∣∣)中的每个向量的长度或大小。范数可以简单的理解为向量的长度,即向量点到坐标零点的距离:
∣ ∣ x i ∣ ∣ 2 = ∣ x i ∣ 2 ||x_i||_2=\sqrt{|x_i|^2} ∣∣xi∣∣2=∣xi∣2
例如,向量 x x x= ( 3 , − 4 ) (3,-4) (3,−4)= [ 3 , − 4 ] T [3,-4]^T [3,−4]T的欧式范数 (Euclidean Norm) 为
∣ ∣ x ∣ ∣ 2 = 3 2 + ( − 4 ) 2 = 5 ||x||_2=\sqrt{3^2+(-4)^2}=5 ∣∣x∣∣2=32+(−4)2=5
这个范数也被称为L2范数,用于表示向量的长度或大小。L2范数是通常意义上的模(距离)。L2范数的本质是欧式距离,即两个向量在每个点相减后的平方和再开方(其中另一个点为坐标零点)
那么,一个向量空间或矩阵的L2范数(m个样本)可以表示为:
∣ ∣ x ∣ ∣ 2 = ∑ i = 1 m ∣ x i ∣ 2 ||x||_2=\sqrt{{\sum_{i=1}^m}|x_i|^2} ∣∣x∣∣2=i=1∑m∣xi∣2
为方便统一,一般的,使用L-P范数表示向量空间或矩阵到零点的P阶闵氏距离(Minkowski Distance):
∣ ∣ x ∣ ∣ P = ( ∑ i = 1 m ∣ x i ∣ P ) 1 P ||x||_P=\left({\sum_{i=1}^m}|x_i|^P\right)^\frac{1}{P} ∣∣x∣∣P=(i=1∑m∣xi∣P)P1
范数实际上就是一种用于向量或矩阵距离度量的数学定义。L-P范数的数学含义是计算向量元素绝对值的p次方和的 1 P \frac{1}{P} P1次幂。范数分为向量范数(二维坐标系)和矩阵范数(多维空间),这里只讨论向量范数
根据 P P P的不同,向量范数分为多种:

上图表示了 P P P从无穷到0变化时三维空间中向量到零点的距离(范数)为1的点构成的图形的变化情况。例如L2范数,即欧氏距离,向量空间中到零点的欧氏距离为1的点构成了一个球面
而二维平面上(以P=2和P=1为例)的向量范数表示的图形如下:

从图中可以直观的得到,随着P越大,等高线围成的图型越接近正方形(正无穷范数);当P=2时,等高线围成的图型变为圆;随着P越小,等高线会越接近坐标零点(负无穷范数)
对于向量 x x x= ( x 1 , x 2 , . . . , x m ) (x_1,x_2,...,x_m) (x1,x2,...,xm),常见的范数有:
1)− ∞ \infty ∞范数:所有向量元素绝对值中的最小值
∣ ∣ x ∣ ∣ − ∞ = arg min i ∣ x i ∣ ||x||_{-\infty}=\arg\min_i|x_i| ∣∣x∣∣−∞=argimin∣xi∣
2)L0范数:L0范数并不是一个真正的范数,L0范数主要用于度量向量中非零元素的个数
∣ ∣ x ∣ ∣ 0 ||x||_0
相关文章:

Scikit-Learn线性回归(五)
Scikit-Learn线性回归五:岭回归与Lasso回归 1、误差与模型复杂度2、范数与正则化2.1、范数2.2、正则化3、Scikit-Learn Ridge回归(岭回归)4、Scikit-Learn Lasso回归1、误差与模型复杂度 在第二篇文章 Scikit-Learn线性回归(二) 中,我们已经给出了过拟合与模型泛化的概念并…...

React(2): 使用 html2canvas 生成图片
使用 html2canvas 生成图片 需求 将所需的内容生成图片div 中包括 svg 等 前置准备 "react": "^18.2.0","react-dom": "^18.2.0","html2canvas": "^1.4.1",实现 <div ref{payRef}></div>const pa…...

CAN物理层协议介绍
目录 编辑 1. CAN协议简介 2. CAN物理层 3. 通讯节点 4. 差分信号 5. CAN协议中的差分信号 1. CAN协议简介 CAN是控制器局域网络(Controller Area Network)的简称,它是由研发和生产汽车电子产品著称的德国BOSCH公司开发的,并最终成为国际标准(ISO11519) ࿰…...
)
华为OD机试真题-计算面积-2023年OD统一考试(C卷)
题目描述: 绘图机器的绘图笔初始位置在原点(0, 0),机器启动后其绘图笔按下面规则绘制直线: 1)尝试沿着横向坐标轴正向绘制直线,直到给定的终点值E。 2)期间可通过指令在纵坐标轴方向进行偏移,并同时绘制直线,偏移后按规则1 绘制直线;指令的格式为X offsetY,表示在横…...
设计模式之策略模式【行为型模式】
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档> 学习的最大理由是想摆脱平庸,早一天就多一份人生的精彩;迟一天就多一天平庸的困扰。各位小伙伴,如果您: 想系统/深入学习某…...

git使用(完整流程)
1. 新建仓库 1.右击 git bash 后 输入 git init (仓库为:当前目录) git init name (仓库为:name文件夹) git clone https://github.com/Winnie996/calculate.git //https2.工作区域 工作目录 3. 添加 提交 git add . //工作区添加至暂存区 git commit -m "注释内容&q…...
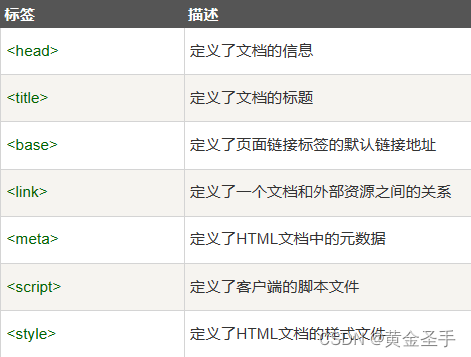
九、HTML头部<head>
一、HTML头部<head> 1、<title>- 定义了HTML文档的标题 使用 <title> 标签定义HTML文档的标题 <!DOCTYPE html> <html><head><meta charset"utf-8"><title>我的 HTML 的第一页</title> </head><b…...
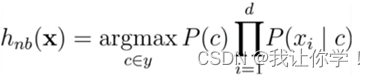
机器学习期末复习
机器学习 选择题名词解释:简答题计算题一、线性回归二、决策树三、贝叶斯 选择题 机器学习利用经验 ,须对以下()进行分析 A 天气 B 数据 C 生活 D 语言 归纳偏好值指机器学习算法在学习的过程中,对以下(&a…...

python-日志模块以及实际使用设计
python-日志模块以及实际使用设计 1. 基本组成 日志模块四个组成部分: 日志对象:产生日志信息日志处理器:将日志信息输出到指定地方,例如终端、文件。格式器:在日志处理器输出之前,对信息进行各方面的美化…...
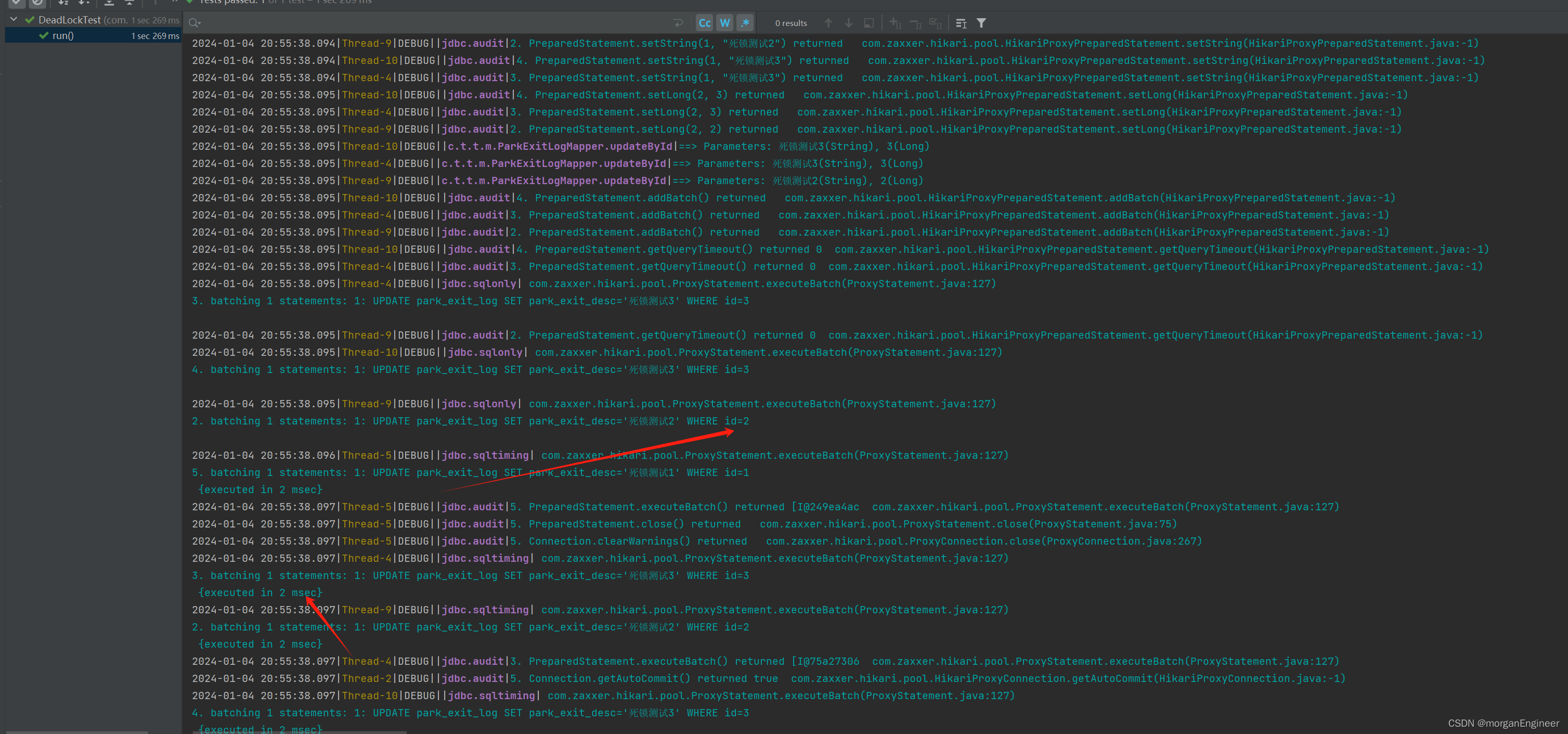
googlecode.log4jdbc慢sql日志,格式化sql
前言 无论使用原生JDBC、mybatis还是hibernate,使用log4j等日志框架可以看到生成的SQL,但是占位符和参数总是分开打印的,不便于分析,显示如下的效果: googlecode Log4jdbc 是一个开源 SQL 日志组件,它使用代理模式实…...
Linux程序、进程和计划任务
目录 一.程序和进程 1.程序的概念 2.进程的概念 3.线程的概念 4.单线程与多线程 5.进程的状态 二.查看进程信息相关命令: 1.ps:查看静态进程信息状态 2.top:查看动态进程排名信息 3.pgrep:查看指定进程 4.pstree&#…...

【MySQL】索引基础
文章目录 1. 索引介绍2. 创建索引 create index…on…2.1 explain2.2 创建索引create index … on…2.3 删除索引 drop index … on 表名 3. 查看索引 show indexes in …4. 前缀索引4.1 确定最佳前缀长度:索引的选择性 5. 全文索引5.1 创建全文索引 create fulltex…...

精确管理Python项目依赖:自动生成requirements.txt的智能方法
在Python中,可以使用几种方法来自动生成requirements.txt文件。这个文件通常用于列出项目所需的所有依赖包及其版本,使其他人或系统可以轻松地重现相同的环境。下面是几种常见的方法: 使用pip freeze: 这是最常见的方法。pip free…...
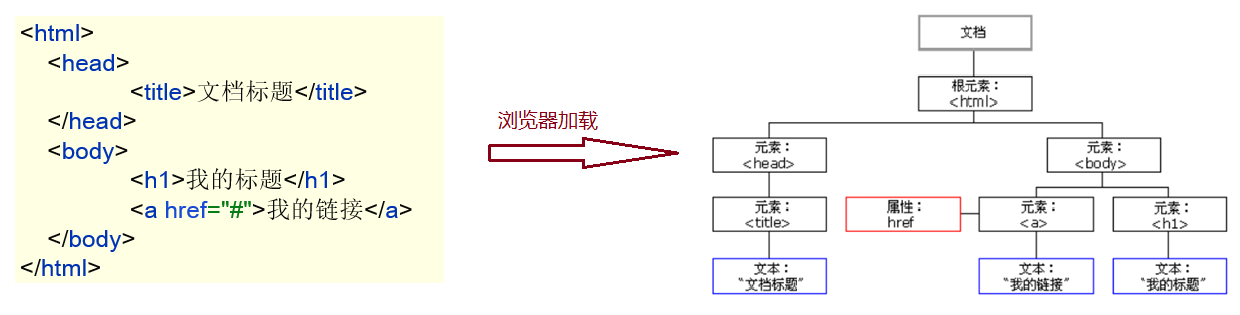
JavaWeb基础(1)- Html与JavaScript(JavaScript基础语法、变量、数据类型、运算符、函数、对象、事件监听、正则表达式)
JavaWeb基础(1)- Html与JavaScript(JavaScript基础语法、变量、数据类型、运算符、函数、对象、事件监听、正则表达式) 文章目录 JavaWeb基础(1)- Html与JavaScript(JavaScript基础语法、变量、数据类型、运算符、函数、对象、事件…...
java SSM体育器材租借管理系统myeclipse开发mysql数据库springMVC模式java编程计算机网页设计
一、源码特点 java SSM体育器材租借管理系统是一套完善的web设计系统(系统采用SSM框架进行设计开发,springspringMVCmybatis),对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要…...

西电期末1030.函数的最大值
一.题目 二.分析与思路 函数打擂台,注意数据类型和保留精度 三.代码实现 #include<bits/stdc.h>//万能头 double f(double x,double a){return a*x*x-x*x*x; }//f(x) int main() {double a;scanf("%lf",&a);double max-1000001;//打擂台for(…...

在Docker中安装Tomact
目录 前言: 一.安装Tomact 查找指定的tomact版本 下载tomact9.0 查看该镜像是否安装成功 安装成功之后就开始运行镜像了 ps(用于列出正在运行的Docker容器) 编辑 测试(虚拟机ip:8080) 编辑 解决措施 编辑 完成以上步骤&…...

【书生大模型00--开源体系介绍】
书生大模型开源体系介绍 0 通用人工智能1 InternLM性能及模型2 从模型到应用 大模型成为目前很热的关键词,最热门的研究方向,热门的应用;ChatGPT的横空出世所引爆,快速被人们上手应用到各领域; 0 通用人工智能 相信使…...

基于GPT-3、ChatGPT、GPT-4等Transformer架构的自然语言处理
文章目录 一、内容简介二、前言2.1 Transformer 模型标志着AI 新时代的开始2.2 Transformer 架构具有革命性和颠覆性2.3 Google BERT 和OpenAI GPT-3 等Transformer 模型将AI 提升到另一个层次2.4 本书将带给你的“芝士”2.5 本书面向的读者 三、本书内容简介3.1 第一章3.2 第二…...

一款开源的MES系统
随着工业4.0的快速发展,制造执行系统(MES)成为了智能制造的核心。今天,将为大家推荐一款开源的MES系统——iMES工厂管家。 什么是iMES工厂管家 iMES工厂管家是一款专为中小型制造企业打造的开源MES系统。它具备高度的可定制性和灵…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...
