《矩阵分析》笔记
来源:【《矩阵分析》期末速成 主讲人:苑长(5小时冲上90+)】https://www.bilibili.com/video/BV1A24y1p76q?vd_source=c4e1c57e5b6ca4824f87e74170ffa64d
这学期考矩阵论,使用教材是《矩阵论简明教程》,因为没时间听太长的课,就看了b站上这个视频,笔记几乎就是原视频copy,和教材相比有一些没提到(如奇异值分解、Householder矩阵、Given矩阵、广义逆矩阵等),但大部分有,可供参考。
目录
- 第1章 线性空间和线性变换
- 考点一:线性空间的基与维数
- 考点二:证明线性变换
- 考点三:像子空间、核子空间(用线性变换定义的子空间)
- 考点四:线性变换的矩阵(求线性变换T在某基底下的矩阵)
- 第2章 内积空间
- 考点一:内积空间的定义
- 考点二:标准正交基
- 考点三:正规矩阵的对角化
- 第3章 矩阵的标准形
- 考点一:哈密顿-凯莱(Hamilton-Cayley)定理
- 考点二:最小多项式
- 考点三:约当标准形(Jordan标准形)
- 考点四:史密斯标准形(Smith标准形)
- 考点五:用史密斯标准形方法求解约当标准形(法二)常用
- 第4章 向量和矩阵的范数
- 考点一:证明向量范数
- 考点二:证明矩阵范数
- 考点三:范数与正规矩阵的证明题
- 第5章 矩阵的分解
- 考点一:矩阵的三角分解
- 考点二:矩阵的QR分解
- 考点三:矩阵的满秩分解
- 第6章 矩阵的函数
- 考点一:矩阵的导数(对一个变量的导数)
- 考点二:矩阵的幂级数
- 考点三:矩阵函数(A-->f(At)) 常见(A-->e~At~)
- 考点四:矩阵函数在微分方程组中的应用
- 考点五:矩阵函数的性质(e^At^-->A)
- 第7章 矩阵特征值的估计
- 考点一:Gerschgorin盖尔圆定理
- 第8章 矩阵的直积(Kronecker积)
- 考点一:直积
- 考点二:拉直
第1章 线性空间和线性变换
考点一:线性空间的基与维数
-
线性空间:若同时满足封闭性和8条规则,则称非空集合V为数域P上的线性空间
-
基底:V中线性无关的一组向量,其他元组都可以被他们线性表示, d i m V = n dimV=n dimV=n
-
子空间:W对于线性空间V所定义的加法运算和数乘运算也构成P上的线性空间,则称W为V的线性子空间,简称子空间
-
生成子空间
设α1,α2,…,αm是V上的m个元素,由这m个元素的任意组合构成的集合{k1α1+k2a2+…kmam}对V中的加法及数乘封闭,因而这个子集是V中的子空间,记作:L(α1,α2,…,αm)
(1)V1∩V2 (2)V1+V2
-
求和子空间的方法
-
维数定理: d i m V 1 + d i m V 2 = d i m ( V 1 + V 2 ) + d i m ( V 1 ∩ V 2 ) dimV~1~+dimV~2~ = dim(V~1~+V~2~) + dim(V~1~∩V~2~) dimV 1 +dimV 2 =dim(V 1 +V 2 )+dim(V 1 ∩V 2 )
【例1.1】求V1+V2的维数及一个基
向量竖写为矩阵,化为阶梯形,一组极大无关组就是一个基,维数为阶梯数
考点二:证明线性变换
-
变换:设V是P上的线性空间,从V到V的映射称为V中的变换(线性变换是常见的变换)
-
线性变换:设T是V上的变换,如果对于任意的α,β∈V,k∈P都有
T ( a + b ) = T a + T b ; T ( k a ) = k T a T(a+b)=Ta+Tb; T(ka) = kTa T(a+b)=Ta+Tb;T(ka)=kTa ,则称T为V上的线性变换
【例1.2】定义变换T如下:TA= CA-AC。证明: T是线性变换
把A替换为a+b、ka,列出T(a+b),Ta+Tb,T(ka),kTa
考点三:像子空间、核子空间(用线性变换定义的子空间)
-
像子空间: T V = T α ∣ α 属于 V TV={Tα|α属于V} TV=Tα∣α属于V
像子空间是由V中所有元素的像Tα构成的(Tα是α通过线性变换T得到的,α∈V)
-
核子空间: T − 1 ( 0 ) = k e r T = α ∣ α ∈ V , T α = 0 T^{-1}(0) = kerT = {α|α∈V,Tα=0} T−1(0)=kerT=α∣α∈V,Tα=0
核子空间中的元素α在线性变换T的作用下转换为0
-
例如:投影变换{(x1, x2, x3)}三维空间
T(x1, x2, x3) = (x1, x2, 0)
TV = {(x1, x2, 0)},二维空间,维数为2
T’(0) = {(0, 0, x3)},一维空间,维数为1
- 维数定理2:设T是n维空间上的线性变换,则 d i m T V = d i m T − 1 ( 0 ) = n dimTV = dimT^{-1}(0)=n dimTV=dimT−1(0)=n
考点四:线性变换的矩阵(求线性变换T在某基底下的矩阵)
-
用矩阵A来表达线性变换T
定义: ( T α 1 , T α 2 , . . . , T α n ) = ( α 1 , α 2 , . . . , α n ) A (Tα_1,Tα_2,...,Tα_n) = (α_1,α_2,...,α_n)A (Tα1,Tα2,...,Tαn)=(α1,α2,...,αn)A
-
求同一个线性变换在不同基底下的矩阵

p.s. 求逆方法:(A|E)–>(E|A-1)
【例1.4】

第2章 内积空间
考点一:内积空间的定义
-
定义:

-
元素大小:

考点二:标准正交基
-
标准正交基:

-
用施密特(Schmidt)正交化的方法求标准正交基

【例2.1】


考点三:正规矩阵的对角化
-
定义:

此时V叫作复内积空间或者酉空间 -
酉矩阵的定义:设A∈Cn×n且AHA=AAH=E,则称A为酉矩阵
-
正规矩阵的定义:设A∈Cn×n且AHA=AAH,则称A为正规矩阵
-
对角形矩阵、实对称矩阵、反实对称矩阵、厄密特矩阵、反厄密特矩阵、正交矩阵、酉矩阵都是正规矩阵
-
正规矩阵对角化:正规矩阵一定可以对角化,即存在酉矩阵U使得UHAU= Λ, Λ的对角线元素为A的特征值
第3章 矩阵的标准形
考点一:哈密顿-凯莱(Hamilton-Cayley)定理
-
哈密顿凯莱定理:每个n阶矩阵都是它的特征多项式的根。
设A为n阶矩阵, f ( λ ) = ∣ λ E − A ∣ = λ n + a n − 1 λ n − 1 + . . . + a 1 λ + a 0 f(λ)=|λE-A|=λ^n +a_{n-1} λ^{n-1}+...+a_1λ+a_0 f(λ)=∣λE−A∣=λn+an−1λn−1+...+a1λ+a0
则 f ( A ) = A n + a n − 1 A n − 1 + . . . + a 1 A + a 0 E = 0 f(A)=A^n+a_{n-1}A^{n-1}+...+a_1A+a_0E=0 f(A)=An+an−1An−1+...+a1A+a0E=0
-
简化运算:求φ(A)
φ ( λ ) = f ( λ ) ⋅ q ( λ ) + r ( λ ) φ(λ)=f(λ)·q(λ)+r(λ) φ(λ)=f(λ)⋅q(λ)+r(λ)
φ ( A ) = f ( A ) ⋅ q ( A ) + r ( A ) = 0 + r ( A ) = r ( A ) φ(A)=f(A)·q(A)+r(A)=0+r(A)=r(A) φ(A)=f(A)⋅q(A)+r(A)=0+r(A)=r(A)
【例3.1】


考点二:最小多项式
-
特征多项式: f ( λ ) = ∣ λ E − A ∣ f(λ)=|λE-A| f(λ)=∣λE−A∣,称为矩阵A的特征多项式
-
零化多项式:若A是一个方针,φ(λ)是一个多项式, φ ( λ ) = a m λ m + a m − 1 λ m − 1 + . . . + a 1 λ + a 0 φ(λ)=a_mλ^m+a_{m-1}λ^{m-1}+...+a_1λ+a_0 φ(λ)=amλm+am−1λm−1+...+a1λ+a0,则称φ(λ)是A的零化多项式
-
特征多项式就是矩阵A的零化多项式;特征多项式×任一多项式还是零化多项式;零化多项式有无穷多个
-
最小多项式:设A∈Cn×n,在A的零化多项式中,次数最低的首项系数为1的多项式,称为矩阵A的最小多项式,记作m(λ)
-
最小多项式的跟<==>特征多项式(对同一矩阵而言)
设矩阵A属于Cn×n的所有特征值λ1,…,λs,A的特征多项式为f(λ)=|λE-A|
则A的最小多项式一定具有如下形式: m ( λ ) = ( λ − λ 1 ) n 1 ( λ − λ 2 ) n 2 . . . ( λ − λ s ) n s m(λ)=(λ-λ_1)^{n_1}(λ-λ_2)^{n_2}...(λ-λ_s)^{n_s} m(λ)=(λ−λ1)n1(λ−λ2)n2...(λ−λs)ns
【例3.2】

考点三:约当标准形(Jordan标准形)
-
λ矩阵:设矩阵A的元素都是λ的多项式,形如

-
行列式因子:A(λ)中所有非零的k阶子式的首项系数为1的最大公因式,D(λ),称为A的一个k级行列式因子
-
不变因子:d1=D1,d2=D2/D1,d3=D3/D2,…,dn=Dn/Dn-1
-
初级因子:把每个次数大于零的不变因子分解为互不相同的一次因式的方幂的乘积,所有这些一次因式的方幂(相同的必须按出现次数计算),称为A的初级因子
-
约当标准形定义:称ri阶矩阵

-
求约当标准形的方法
- 法一:用行列式因子法
【例3.3】

(二阶有9个,略)

考点四:史密斯标准形(Smith标准形)
-
矩阵A的初等变换
-
互换矩阵A的任意两行/列
-
以非零的数k乘A的某一行/列
-
以多项式φ(λ)乘以A的某一行/列,加到另一行/列上
(以上三种变换不会改变行列式因子)
-
-
史密斯标准形:

-
任一个非零多项式矩阵A都可以经过初等变换化为史密斯标准形
-
化为史密斯标准形的具体步骤
-
先确定左上角第一个元素d1=D1(一阶行列式因子)
-
将d1所在的行和列的其他元素都消为0(通过初等变换),得到
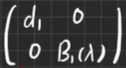
-
再确定新矩阵B1(λ)的左上角第一个元素d2=新D1‘(新D1‘为新矩阵B1(λ)的一阶行列式因子)
得到

-
重复这个过程,即可得到史密斯标准形

-
【例3.4】求Smith标准形和不变因子

考点五:用史密斯标准形方法求解约当标准形(法二)常用
- 史密斯标准形
【例3.5】求约当标准形


第4章 向量和矩阵的范数
考点一:证明向量范数
- 向量范数的定义:

则称||x||为Cn上的向量范数,简称向量范数
- 常用的向量范数

【例4.1】

考点二:证明矩阵范数
1.矩阵范数的定义:

-
常用的矩阵范数


-
相容性:

-
谱半径:

-
谱半径与范数:
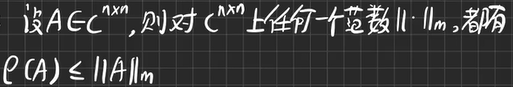
【例4.2】

考点三:范数与正规矩阵的证明题
-
正规矩阵对角化:正规矩阵一定可以对角化,即存在酉矩阵U使得UHAU= Λ, Λ的对角线元素为A的特征值
【例4.3】

第5章 矩阵的分解
考点一:矩阵的三角分解
-
Dolittle分解法(A=LR)
矩阵特点(以三阶为例)
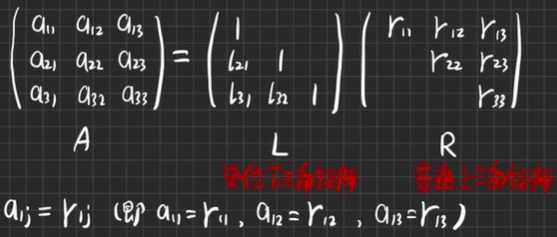
【例5.1】求矩阵的Dolittle分解

考点二:矩阵的QR分解
-
QR分解定理:A=QR(A: n阶复矩阵,Q: 酉矩阵,R: 上三角矩阵)
-
QR分解的一般步骤(以三阶方矩为例)
-
把矩阵A写成列向量的形式:A=(α1,α2,α3)
-
用施密特正交化方法,把α1,α2,α3正交化
-
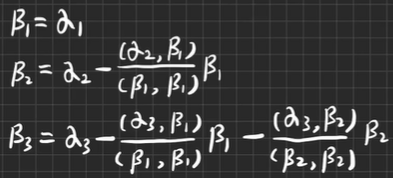


-
【例5.2】 求矩阵的QR分解



考点三:矩阵的满秩分解
-
满秩分解:将矩阵A分解为列满秩×行满秩矩阵,形如:

-
满秩分解的一般步骤
- 作初等行变换:


- 作初等行变换:
【例5.3】求矩阵的满秩分解



第6章 矩阵的函数
考点一:矩阵的导数(对一个变量的导数)
-
函数矩阵:以实变量t的实函数aij(t)为元素的矩阵

-
函数矩阵对一个变量的导数
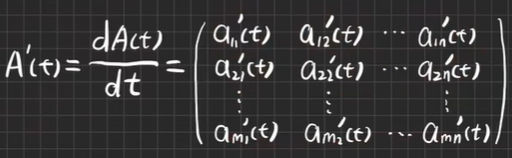
【例6.1】求dA/dt

考点二:矩阵的幂级数
-
矩阵幂级数:设 A = ( a i j ∈ C n × n ) A=(a_{ij}∈C^{n×n}) A=(aij∈Cn×n),称形如
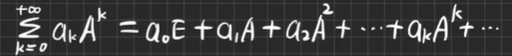
-
收敛性:设幂级数Σk=0akxk的收敛半径为R,A∈Cn×n则
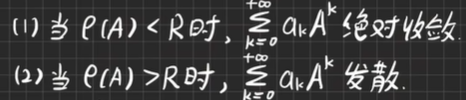
-
收敛半径:R=1/ρ,ρ=limk->∞=|ak+1/ak|
【例6.2】判断矩阵幂级数

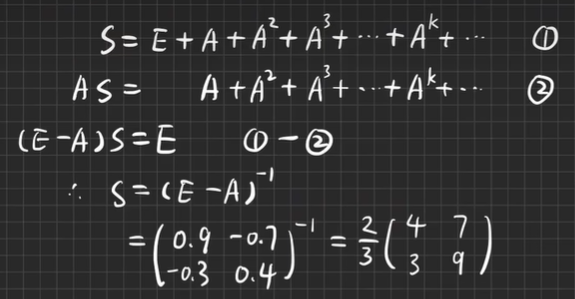
考点三:矩阵函数(A–>f(At)) 常见(A–>eAt)
-
计算矩阵函数的方法:最小多项式法
-
计算矩阵函数的一般步骤:

【例6.3】求矩阵函数eAt




考点四:矩阵函数在微分方程组中的应用
-
一阶线性常系数齐次微分方程组
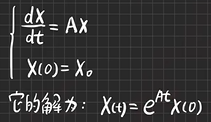
-
一阶线性常系数非齐次微分方程组
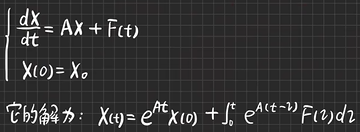
【例6.4】




考点五:矩阵函数的性质(eAt–>A)
- deAt/dt=AeAt=eAtA,则[deAt/dt]|t=0=AdeA·0=Ae0=A
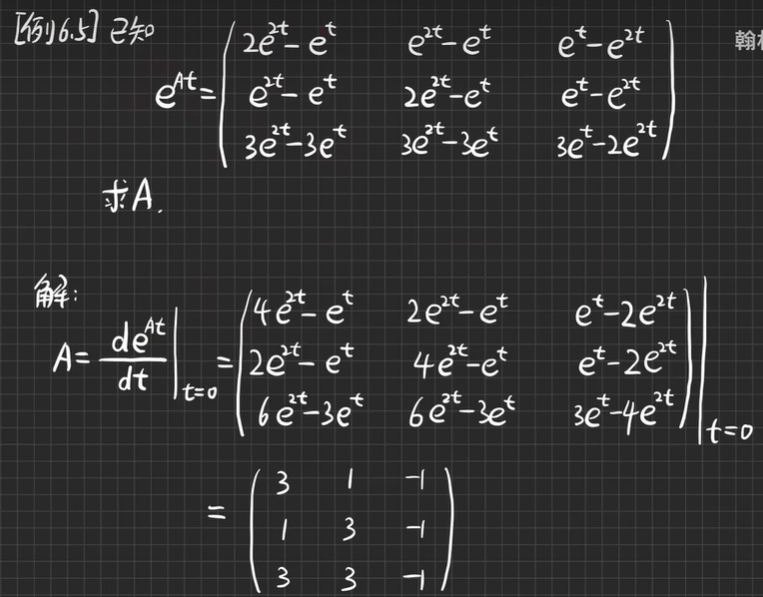
第7章 矩阵特征值的估计
考点一:Gerschgorin盖尔圆定理
-
盖尔圆定义

-
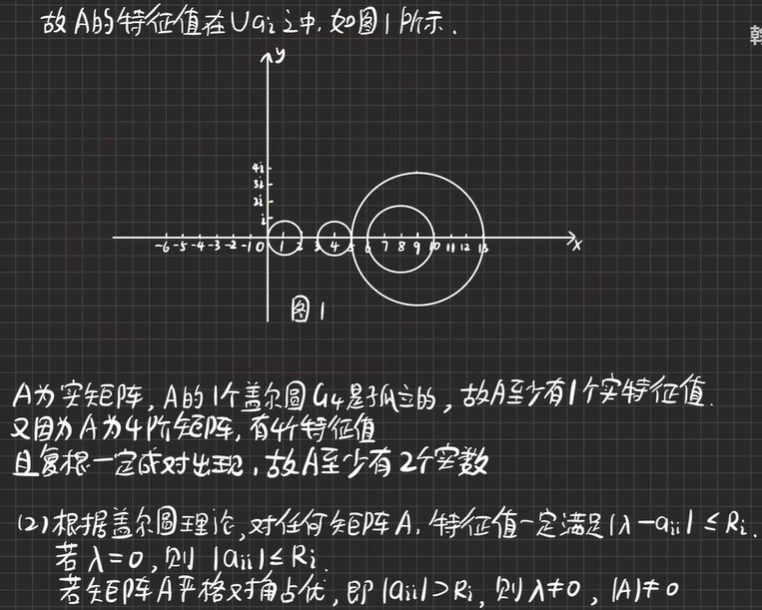
盖尔圆定理:矩阵A∈Cn×n的全体特征值都在它的n个盖尔圆构成的并集之中
-
A的列盖尔圆:A∈Cn×n与AT的特征值相同,根据盖尔圆定理A的特征值也在AT的n个盖尔圆构成的并集之中,称AT的盖尔圆为A的列盖尔圆
【例7.1】估计矩阵的特征分布
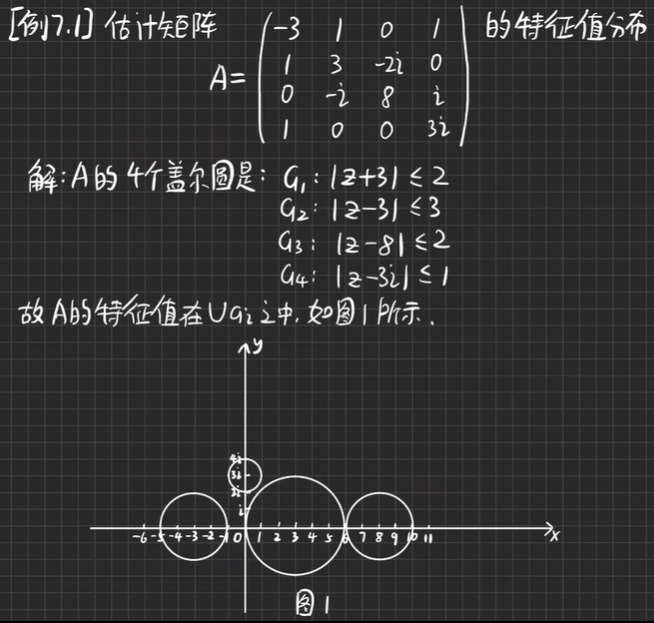

- 推论:若A为实矩阵A∈Rn×n,且A的n个盖尔圆是孤立的,则A有n个互不相同的实特征值
【例7.2】画出矩阵盖尔圆草图、矩阵能够对角化吗?


-
根据盖尔圆理论,对任何矩阵A,特征值一定满足|λaii|≤Ri,
若λ=0,则|λaii|≤Ri,
若矩阵A严格对角占优,即|λaii|>Ri,则λ≠0,|A|≠0
-
A为实矩阵,特征方程|λE-A|=0为实代数方程,它的复根一定成对出现,一定是共轭的,即a±ib的形式
【例7.3】

第8章 矩阵的直积(Kronecker积)
考点一:直积
- 直积的定义:设矩阵A=(aij)m×n,B=(bij)p×q,

【例8.1】

- 矩阵直积的性质


【例8.2】求A⊗B的一个特征值和特征向量

【例8.3】

【例8.4】

考点二:拉直
-
拉直的定义:
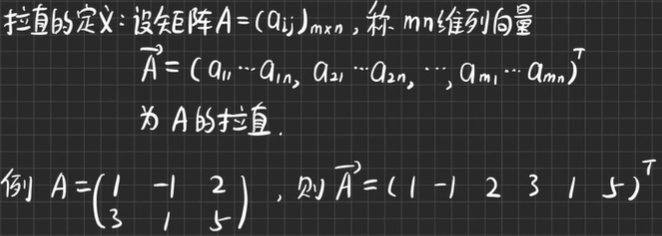
-
拉直的性质:
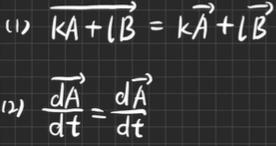
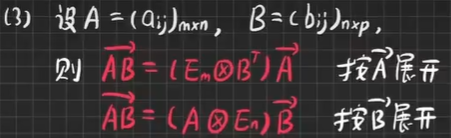
(改错) A B ( 拉直 ) = ( A ⊗ E p ) B ( 拉直 ) AB(拉直)=(A⊗E~p~)B(拉直) AB(拉直)=(A⊗E p )B(拉直)(按B展开)- 定理
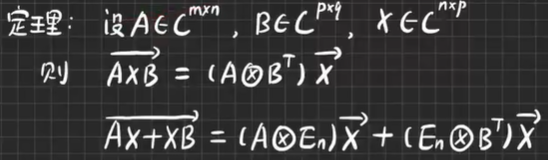
A ⊗ E n − ( 改为 ) − > A ⊗ E p A⊗E~n-(改为)->A⊗E~p A⊗E n−(改为)−>A⊗E p
- 定理
【例8.5】

∵ ( A ⊗ B ) ( x ⊗ y ) = ( A x ) ⊗ ( B y ) ∴ ( A ⊗ E n ) ( E m ⊗ B T ) = ( A ⊗ B T ) ∵(A⊗B)(x⊗y)=(Ax)⊗(By) ∴(A⊗En)(Em⊗BT)=(A⊗BT) ∵(A⊗B)(x⊗y)=(Ax)⊗(By)∴(A⊗En)(Em⊗BT)=(A⊗BT)
- 线性矩阵方程组:设A∈Cm×m,B∈Cn×n,F∈Cm×n,X∈Cm×n

【例8.6】

相关文章:

《矩阵分析》笔记
来源:【《矩阵分析》期末速成 主讲人:苑长(5小时冲上90)】https://www.bilibili.com/video/BV1A24y1p76q?vd_sourcec4e1c57e5b6ca4824f87e74170ffa64d 这学期考矩阵论,使用教材是《矩阵论简明教程》,因为没…...

『App自动化测试之Appium应用篇』| Appium常用API及操作
『App自动化测试之Appium应用篇』| Appium常用API及操作 1 press_keycode1.1 键盘操作1.2 关于KeyCode1.3 press_keycode源码1.4 电话键相关1.5 控制键相关1.6 基本按键相关1.7 组合键相关1.8 符号键相关1.9 使用举例 2 swip方法2.1 swip说明2.2 swip使用方法2.3 使用示例 3 sc…...
VSCode搭建 .netcore 开发环境
一、MacOS 笔者笔记本电脑上安装的是macOS High Sierra(10.13),想要尝试一下新版本的.netcore,之前系统是10.12时,.netcore 3.1刚出来时安装过3.1版本,很久没更新了,最近.net8出来了,想试一下,…...
python 写自动点击爬取数据
今天来点不一样的!哥们 提示: 这里只是用于自己学习的 ,请勿用违法地方 效果图 会进行点击下一页 进行抓取 需要其他操作也可以自己写 文章目录 今天来点不一样的!哥们前言一、上代码?总结 前言 爬虫是指通过编程自动…...
CSDN博客重新更新
说来惭愧,好久没更新博客文章,导致个人博客网站:https://lenky.info/ 所在的网络空间和域名都过期了都没发觉,直到有个同事在Dim上问我我的个人博客为啥打不开了。。。幸好之前有做整站备份,后续慢慢把内容都迁回CSDN上…...
)
《剑指 Offer》专项突破版 - 面试题 5 : 单词长度的最大乘积(C++ 实现)
目录 前言 方法一 方法二 前言 题目链接:318. 最大单词长度乘积 - 力扣(LeetCode) 题目: 输入一个字符串数组 words,请计算不包含相同字符的两个字符串 words[i] 和 words[j] 的长度乘积的最大值。如果所有字符串…...

【Java集合篇】HashMap的get方法是如何实现的?
HashMap的get方法是如何实现的 ✔️典型解析✔️拓展知识仓✔️如何避免HashMap get方法的哈希重✔️HashMap get方法的优缺点有哪些✔️HashMap get方法的是线程安全的吗✔️什么是ConcurrentHashMap✔️ConcurrentHashMap有哪些应用场景✔️ConcurrentHashMap的优缺点 ✔️源…...
Java学习苦旅(二十二)——MapSet
本篇博客将详细讲解Map和Set。 文章目录 搜索概念模型 MapMap.Entry<K, V>Map的常用方法说明TreeMap和HashMap的区别 Set常用方法说明TreeSet和HashSet的区别 结尾 搜索 概念 Map和set是一种专门用来进行搜索的容器或者数据结构,其搜索的效率与其具体的实例…...

【Linux Shell】12. 文件包含
和其他语言一样,Shell 也可以包含外部脚本,这样可以很方便的封装一些公用的代码作为一个独立的文件。可以理解为在第2个文件中包含第1个文件,执行第1个文件的代码。 被包含的文件 不需要可执行权限 。Shell 文件包含的语法格式如下࿱…...

前端-基础 常用标签-超链接标签( 锚点链接 )
锚点链接 : 点击链接,可以快速定位到 页面中的某个位置 如果不好理解,讲一个例子,您就马上明白了 >>> 这个是 刘德华的百度百科 ,可以看到,页面里面有很多内容,那就得有个目录了 …...
2024--Django平台开发-基础信息(一)
一、前置知识点 - Python环境搭建 (Python解释器、Pycharm、环境变量等) - 基础语法(条件、循环、输入输出、编码等) - 数据类型(整型、布尔型、字符串、列表、字典、元组、集合等) - 函数(文件操作、返回值、参数、作用域等) - 面向对象 (类、对象、封装、继承、多态等)包和模…...

C++力扣题目--94,144,145二叉树递归遍历
思路 这次我们要好好谈一谈递归,为什么很多同学看递归算法都是“一看就会,一写就废”。 主要是对递归不成体系,没有方法论,每次写递归算法 ,都是靠玄学来写代码,代码能不能编过都靠运气。 本篇将介绍前后…...

开源游戏引擎:创造无限可能 | 开源专题 No.56
godotengine/godot Stars: 62.6k License: MIT Godot Engine 是一个功能强大的跨平台游戏引擎,可用于创建 2D 和 3D 游戏。它提供了一套全面的常见工具,让用户可以专注于制作游戏而不必重复造轮子。该引擎支持将游戏一键导出到多个平台上,包…...
MyBatisPlus学习一:快速入门
前言 前面快速学习了Mybatis,现在开始快速学习MyBatisPlus 学习教程: 黑马mybatis教程全套视频教程,2天Mybatis框架从入门到精通 黑马程序员最新MybatisPlus全套视频教程,4小时快速精通mybatis-plus框架 简介 MyBatisPlus 是…...
2024最新外贸建站:ChemiCloud主机购买使用及自建外贸独立站教程
随着电商平台竞争的加剧,许多外贸从业者意识到减少对平台依赖的重要性,并选择搭建自己的外贸独立站来获得更多的控制权和灵活性。即使是没有建站基础的新手,也可以通过学习建站来实现这一目标。下面是一个适用于新手的外贸建站教程࿰…...
校招社招,认知能力测验,③如何破解语言常识类测试题?
作为认知能力测评中的一个环节,语言常识类,是大概率的出现,不同的用人单位可能略有不同,语言是一切的基础,而常识则意味着我们的知识面的宽度。 语言常识类的测试,如果要说技巧?难说....更多的…...

了解一下InternLM2
大模型的出现和发展得益于增长的数据量、计算能力的提升以及算法优化等因素。这些模型在各种任务中展现出惊人的性能,比如自然语言处理、计算机视觉、语音识别等。这种模型通常采用深度神经网络结构,如 Transformer、BERT、GPT( Generative P…...

关于使用统一服务器,vscode和网页版jupyter notebook的交互问题
autodl 查看虚拟环境 在antodl上租借了一个服务器,通过在网页上运行jupyter notebook和在vscode中运行,发现环境都默认的是miniconda3。 conda info --envs 当然环境中所有的包都是一样的。 要查看当前虚拟环境中安装的所有包,可以使用以…...

Linux22.04系统安装显卡驱动,cuda,cudnn流程
1. 安装显卡驱动 ubuntu-drivers deices显示所有适配显卡的驱动型号,recommended为推荐安装 安装 sudo apt install nvidia-driver-440重启 sudo reboot验证 nvidia-smi2. 安装cuda 在 CUDA Toolkit 的下载页面选择系统版本和安装方式,下载并运行…...

【常考简答题】操作系统
目录 1、什么是进程 2、创建进程步骤 3、什么是死锁 4、死锁四个必要条件 5、什么是内存管理 6、内存管理功能 7、进程的三个基本状态转化图 8、操作系统为什么引入线程 9、什么是对换技术,好处是什么 10、DMA直接存取控制工作方式流程图 11、什么是假脱…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...
