【代码随想录】刷题笔记Day47
前言
- 又过了个愉快的周末~大组会终于不用开了,理论上已经可以回家了!但是我多留学校几天吧,回家实在太无聊了,也没太多学习的氛围
198. 打家劫舍 - 力扣(LeetCode)
- dp[i]含义
- 考虑下标i(包括i)以内的房屋,最多可以偷窃的金额为dp[i]
- 递推公式:包含偷和不偷
- dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
- 初始化
- dp[0] = nums[0],dp[1] = max(nums[0], nums[1]);
- 遍历顺序:类似斐波那契,从前往后推导
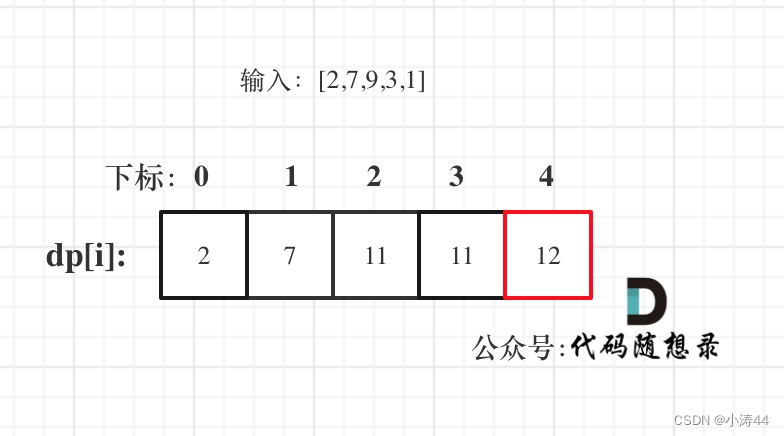
-
class Solution { public:int rob(vector<int>& nums) { if(nums.size() == 1) return nums[0];vector<int> dp(nums.size());dp[0] = nums[0];dp[1] = max(nums[0], nums[1]);for(int i = 2; i < nums.size(); i++){dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);}return dp[nums.size() - 1];} };
213. 打家劫舍 II - 力扣(LeetCode)
- 本题难点在于将环形问题拆解成线性问题,分为三种情况
- 情况一:考虑不包含首尾元素
- 情况二:考虑包含首元素,不包含尾元素
- 情况三:考虑包含尾元素,不包含首元素
- 情况二、三是包含情况一的,所以把掐头去尾的数组传到上一题取最大值便可
-
// 方法一:传掐头去尾的数组 class Solution { public:int rob(vector<int>& nums) {if (nums.size() == 0) return 0;if (nums.size() == 1) return nums[0];int result1 = robRange(nums, 0, nums.size() - 2); // 情况二int result2 = robRange(nums, 1, nums.size() - 1); // 情况三return max(result1, result2);}// 198.打家劫舍的逻辑int robRange(vector<int>& nums, int start, int end) {if (end == start) return nums[start];vector<int> dp(nums.size());dp[start] = nums[start];dp[start + 1] = max(nums[start], nums[start + 1]);for (int i = start + 2; i <= end; i++) {dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);}return dp[end];} }; - 还有一个很妙的方法,遍历一次,同时更新两个dp数组(掐头 + 去尾)
-
class Solution { public:int rob(vector<int>& nums) {int n = nums.size();if(n == 1) return nums[0];vector<int> dp1(n), dp2(n);// 掐头,考虑1 ~ n-1,取n-1dp1[0] = 0; dp1[1] = nums[1];// 去尾,考虑0 ~ n-2,取n-2dp2[0] = nums[0];dp2[1] = max(nums[0], nums[1]);for(int i = 2; i <= n - 1; i++){dp1[i] = max(dp1[i - 2] + nums[i], dp1[i - 1]);if(i <= n - 2){dp2[i] = max(dp2[i - 2] + nums[i], dp2[i - 1]);}}return max(dp1[n - 1], dp2[n - 2]);} };
337. 打家劫舍 III - 力扣(LeetCode)
- 树形dp入门题目,记录每个节点偷和不偷的状态,递归后序遍历将最优解集中到根节点上
-
dp数组是一个长度为2的数组,在递归的过程中,系统栈会保存每一层递归的参数
-
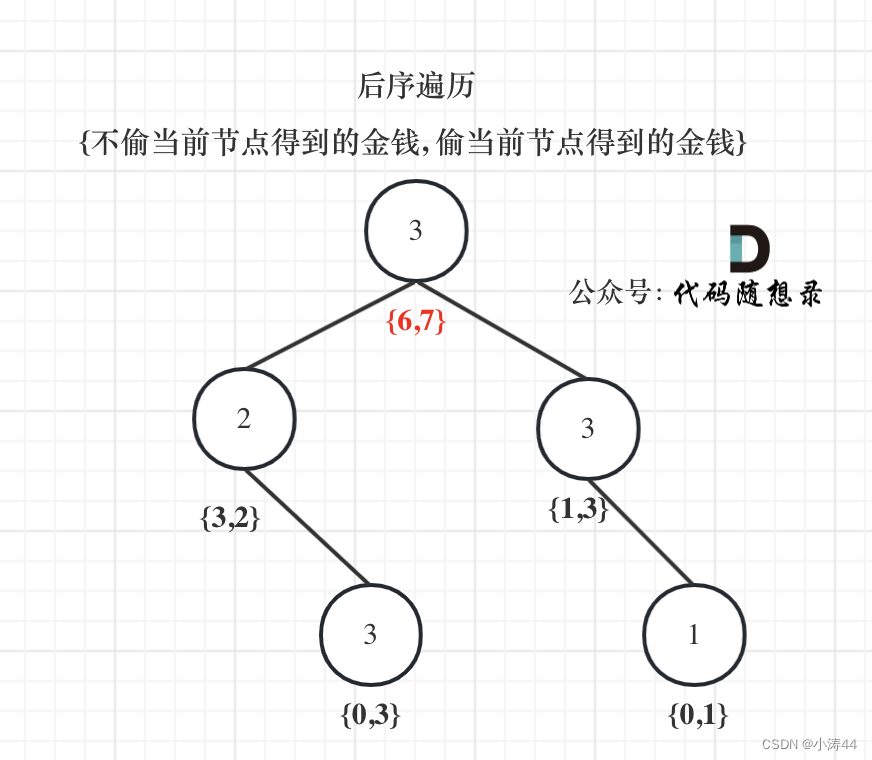
-
class Solution { public:int rob(TreeNode* root) {vector<int> result = robTree(root);return max(result[0], result[1]);}// 长度为2的数组,0:不偷,1:偷vector<int> robTree(TreeNode* root){if(root == nullptr) return {0, 0};vector<int> left = robTree(root->left);vector<int> right = robTree(root->right);// 不偷cur,那么可以偷也可以不偷左右节点,则取较大的情况int val0 = max(left[0], left[1]) + max(right[0], right[1]);// 偷cur,那么就不能偷左右节点。int val1 = root->val + left[0] + right[0];return {val0, val1};} };
后言
- 下周考科二科三,这周得频繁去练车,争取每天早上刷题、下午练车,晚上干活!
相关文章:

【代码随想录】刷题笔记Day47
前言 又过了个愉快的周末~大组会终于不用开了,理论上已经可以回家了!但是我多留学校几天吧,回家实在太无聊了,也没太多学习的氛围 198. 打家劫舍 - 力扣(LeetCode) dp[i]含义 考虑下标i(包括…...

6.1 截图工具HyperSnap6简介
图片是组成多媒体作品的基本元素之一,利用图片可以增强多媒体作品的亲和力和说说服力。截取图片最简单的方法是直接按下键盘上的“PrintScreen”键截取整个屏幕或按下“AltPrintScreen”组合键截取当前活动窗口,然后在画笔或者其它的图片处理软件中进行剪…...
stable diffusion 人物高级提示词(二)衣物、身材
一、衣服大类 英文中文Shirt衬衫Blouse女式衬衫Dress连衣裙Skirt裙子Pants裤子Jeans牛仔裤Swimsuit泳衣Underwear内衣Bra文胸Panties内裤Stockings长筒袜Shoes鞋子Socks袜子 二、细分分类 dress 是连衣裙: 英文解释Formal Dress正式礼服,通常用于正式…...
外包做了1个月,技术退步一大半了。。。
先说一下自己的情况,本科生,20年通过校招进入深圳某软件公司,干了接近4年的功能测试,今年年初,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落!而我已经在一个企业干了四年的功能测试…...

docker-compose常用命令及.yaml配置模板
1、docker-compose常用命令: docker-compose -f mysql-docker-compose.yaml up -d docker-compose -f mysql-docker-compose.yaml downdocker-compose的常用命令包括: docker-compose up:启动并运行Compose文件中的服务。 docker-compose st…...
工作随机:OEM(13.5)报错代理无法访问
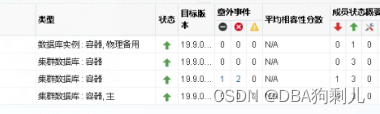
文章目录 前言一、问题排查二、重启主机agent1.定位主机安装位置2.查看并启动agent3.OEM检查 前言 今早接到反馈,在客户部署的OEM(版本 13.5)监控失效,提示代理无法访问,无法访问的除了数据库以外还有主机都显示数据不…...

Pruning Papers
[ICML 2020] Rigging the Lottery: Making All Tickets Winners 整个训练过程中mask是动态的,有drop和grow两步,drop是根据权重绝对值的大小丢弃,grow是根据剩下激活的权重中梯度绝对值生长没有先prune再finetune/retrain的两阶段过程 Laye…...

C#COM对象的资源释放
在C#中使用COM对象时,由于COM对象遵循引用计数(Reference Counting)的管理方式,当COM对象的引用计数为0时,系统才会真正释放该COM对象所占用的资源。然而,在.NET环境下,CLR(Common L…...
了解Apache 配置与应用
本章内容 理解 Apache 连接保持 掌握 Apache 的访问控制 掌握 Apache 日志管理的方法 Apache HTTP Server 之所以受到众多企业的青睐,得益于其代码开源、跨平台、功能 模块化、可灵活定制等诸多优点,不仅性能稳定,在安全性方面的表现也十分…...

悟的复杂度分析
复杂度分析: 时间复杂度(算法中的基本操作的执行次数); 空间复杂度。 时间复杂度: 实际上我们计算时间复杂度时,我们其实并不需要计算准确的执行次数,只需要大概的执行次数,因此我们…...
《网络是怎样连接的》2.5节图表(自用)
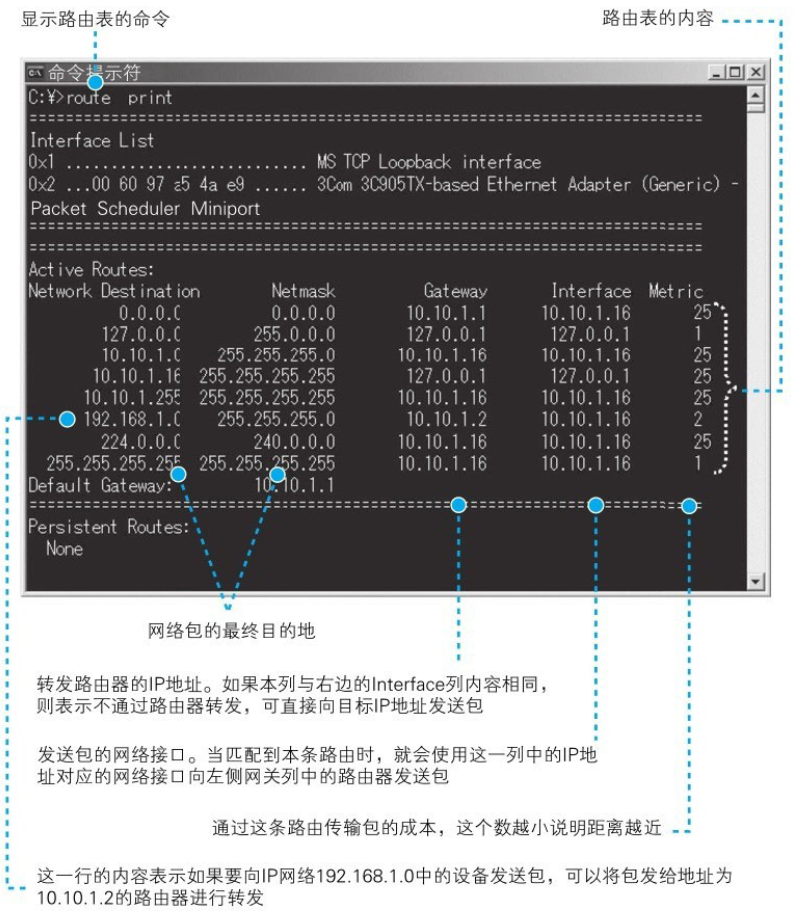
图5.1:ip包结构 图5.2:ip网络包的传输方式 1.以太网的部分也可以替换成其他的东西,例如无线局域网、ADSL、FTTH等,它们都可以替代以太网的角色帮助IP协议来传输网络包 2.根据ARP协议,客户端可以根据ip地址得到下一个路…...
java 音乐会售票平台系统Myeclipse开发mysql数据库struts2结构java编程计算机网页项目
一、源码特点 java 音乐会售票平台系统 是一套完善的web设计系统,对理解JSP java编程开发语言有帮助struts2框架开发mvc模式,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。开发 环境为TOCAT7.0,Myeclipse8.5开发,数据…...
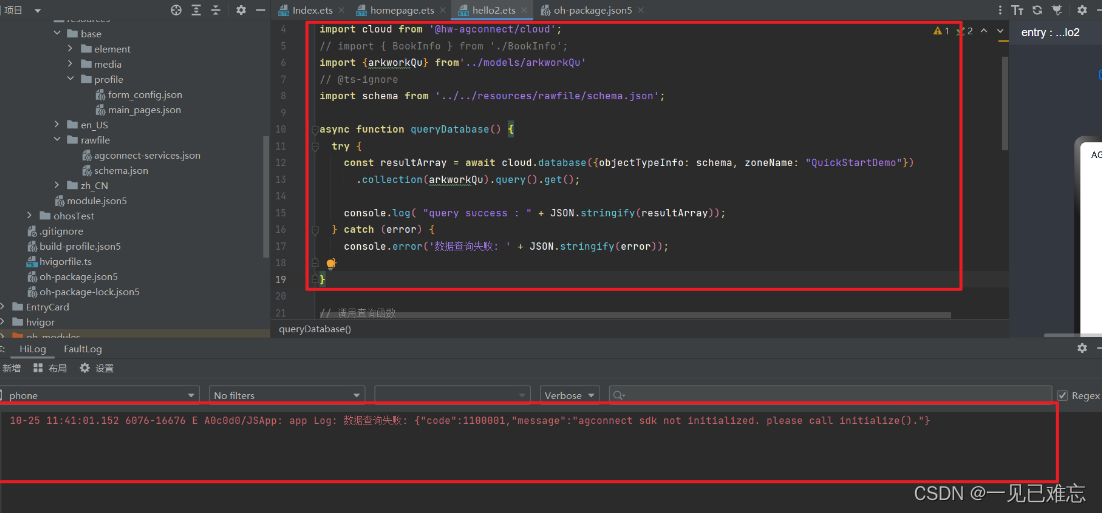
鸿蒙开发解决agconnect sdk not initialized. please call initialize()
文章目录 项目场景:问题描述原因分析:解决方案:总结:项目场景: 鸿蒙开发报错: agconnect sdk not initialized. please call initialize() 问题描述 报错内容为: 10-25 11:41:01.152 6076-16676 E A0c0d0/JSApp: app Log: 数据查询失败: {“code”:1100001,“messag…...

秋招阿里巴巴java笔试试题-精
一、单项选择题 1、以下函数的时间复杂度是 ( ) 1 2 3 4 5 6 7 8 9 void func(int x,int y, int z){ if(x<0) printf("%d, %d\n", y, z); else { func(x-1,y1,z); func(x-1,y,z1); } } A.O(x*y*z) B.O(x^2*y^2) C.O(2^x) D.O(2^x*…...

018、通用集合类型
Rust标准库包含了一系列非常有用的被称为集合的数据结构。大部分的数据结构都代表着某个特定的值,但集合却可以包含多个值。 与内置的数组与元组类型不同,这些集合将自己持有的数据存储在了堆上。这意味着数据的大小不需要在编译时确定,并且可…...
【Leetcode】236.二叉树的最近公共祖先
一、题目 1、题目描述 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。 百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。” 示例1…...
C#,入门教程(11)——枚举(Enum)的基础知识和高级应用
上一篇: C#,入门教程(10)——常量、变量与命名规则的基础知识https://blog.csdn.net/beijinghorn/article/details/123913570 不会枚举,就不会编程! 枚举 一个有组织的常量系列 比如:一个星期每一天的名字…...
java SSM水质历史数据可视化设计myeclipse开发mysql数据库springMVC模式java编程计算机网页设计
一、源码特点 java SSM水质历史数据可视化设计是一套完善的web设计系统(系统采用SSM框架进行设计开发,springspringMVCmybatis),对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统主…...

C++推箱子游戏开发
游戏 自动地图生成背景音乐推箱子到目标位置 美工资源 美工资源: 链接:https://pan.baidu.com/s/1MZv8pDBXdNDbXxuAAPSM-A **提取码:**2syq 图形库: www.easyx.cn cpp文件 #include "box_man.h" #include <conio.h> #…...

Kotlin函数式接口
函数式接口 接口只有一个抽象方法的接口,称为 函数式接口 functional interface,也叫做 Single Abstract Method(SAM) interface。 注:函数式接口,只有一个抽象方法,但可以有多个非抽象方法。 一、Kotlin Kotlin支持…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...