LeetCode 84:柱状图中的最大矩形
一、题目描述
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
示例 1:

输入:heights = [2,1,5,6,2,3] 输出:10 解释:最大的矩形为图中红色区域,面积为 10
示例 2:
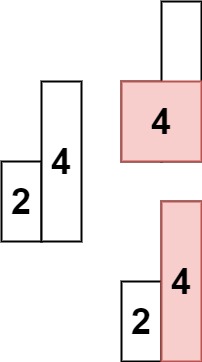
输入: heights = [2,4] 输出: 4
提示:
1 <= heights.length <=1050 <= heights[i] <= 104
二、思路分析
使用栈空间来解决本题,通过空间换时间的方式。
三、代码参考
1、Java
class Solution {public int largestRectangleArea(int[] heights) {// 获取数组长度int len = heights.length;// 数组长度为 0 或者 1 时直接返回if(len == 0){return 0;}if(len == 1){return heights[0];}// 用来返回最大面积,初始值为 0int area = 0;// 创建栈空间做辅助Deque<Integer> stack = new ArrayDeque<>();// 循环遍历数组for(int i = 0; i < len; i++){// while(!stack.isEmpty() && heights[stack.peekLast()] > heights[i]){// 获取栈顶高度,并移除当前栈顶int height = heights[stack.removeLast()];// 做特殊的处理,如果当前栈顶的高度和上一个栈顶的高度相同,则也需要进行弹栈while(!stack.isEmpty() && heights[stack.peekLast()] == height){// 移除栈顶元素stack.removeLast();}// 创建宽度变量,初始值为 0int width = 0;// 如果栈为空,说明,有效柱体能够从 i 的左边一直延伸到第一个开始if(stack.isEmpty()){// 所以此时的宽度为 iwidth = i;}else {width = i - stack.peekLast() - 1;}// 计算面积, 长 * 宽,并获取最大面积area = Math.max(area, height * width);}// 将下标存入栈空间中stack.addLast(i);}// 将当前栈中的所有元素弹出while(!stack.isEmpty()){// 获取栈顶高度,并移除当前栈顶int height = heights[stack.removeLast()];// 做特殊的处理,如果当前栈顶的高度和上一个栈顶的高度相同,则也需要进行弹栈while(!stack.isEmpty() && heights[stack.peekLast()] == height){// 移除栈顶元素stack.removeLast();}// 创建宽度变量,初始值为 0int width = 0;// 如果栈为空,说明,有效柱体能够从 i 的左边一直延伸到第一个开始if(stack.isEmpty()){// 所以此时的宽度为 lenwidth = len;}else {width = len - stack.peekLast() - 1;}// 计算面积, 长 * 宽,并获取最大面积area = Math.max(area, height * width);}// 返回面积结果return area;}
}2、Python
class Solution:def largestRectangleArea(self, heights: List[int]) -> int:size = len(heights)area = 0stack = []for i in range(size):while len(stack) > 0 and heights[i] < heights[stack[-1]]:height = heights[stack.pop()]while len(stack) > 0 and height == heights[stack[-1]]:stack.pop()if len(stack) > 0:width = i - stack[-1] - 1else:width = iarea = max(area, height * width)stack.append(i)while len(stack) > 0 is not None:height = heights[stack.pop()]while len(stack) > 0 and height == heights[stack[-1]]:stack.pop()if len(stack) > 0:width = size - stack[-1] - 1else:width = sizearea = max(area, height * width)return area相关文章:

LeetCode 84:柱状图中的最大矩形
一、题目描述 给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。 求在该柱状图中,能够勾勒出来的矩形的最大面积。 示例 1: 输入:heights [2,1,5,6,2,3] 输出:10 解释:…...

老生重谈:大模型的「幻觉」问题
一、什么是大模型「幻觉」 大模型的幻觉问题通常指的是模型在处理输入时可能会产生一些看似合理但实际上是错误的输出,这可能是因为模型在训练时过度拟合了训练数据,导致对噪声或特定样本的过度敏感。 "大数据幻觉"指的是在处理大规模数据时…...

golang实现skiplist 跳表
跳表 package mainimport ("errors""math""math/rand" )func main() {// 双向链表///**先理解查找过程Level 3: 1 6Level 2: 1 3 6Level 1: 1 2 3 4 6比如 查找2 ; 从高层往下找;如果查找的值比当前值小 说明没有可查找的值2比1大 往当前…...
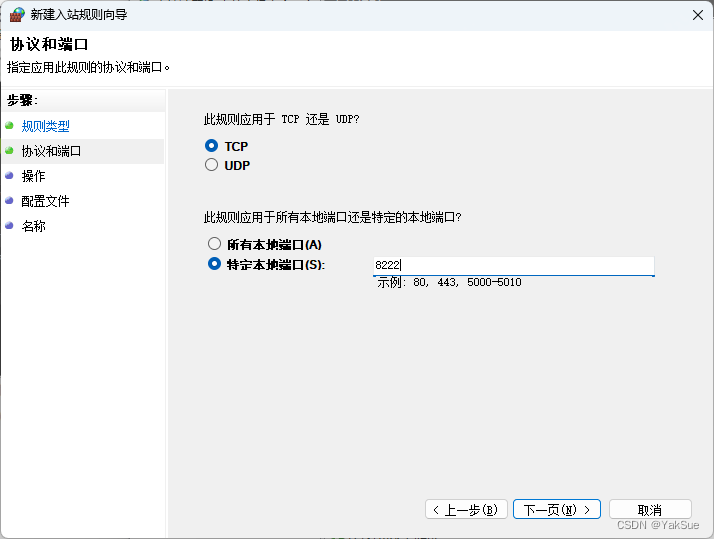
尝试OmniverseFarm的最基础操作
目标 尝试OmniverseFarm的最基础操作。本地机器作为Queue和Agent,同时在本地提交任务。 主要参考了官方文档: Farm Queue — Omniverse Farm latest documentation Farm Agent — Omniverse Farm latest documentation Farm Examples — Omniverse Far…...
)
第28关 k8s监控实战之Prometheus(二)
------> 课程视频同步分享在今日头条和B站 大家好,我是博哥爱运维。 这节课我们用prometheus-operator来安装整套prometheus服务 https://github.com/prometheus-operator/kube-prometheus/releases 开始安装 1. 解压下载的代码包 wget https://github.com/…...

基于 SpringBoot + magic-api + Vue3 + Element Plus + amis3.0 快速开发管理系统
Tansci-Boot 基于 SpringBoot2 magic-api Vue3 Element Plus amis3.0 快速开发管理系统 Tansci-Boot 是一个前后端分离后台管理系统, 前端集成 amis 低代码前端框架,后端集成 magic-api 的接口快速开发框架。包含基础权限、安全认证、以及常用的一…...

Kafka(四)Broker
目录 1 配置Broker1.1 Broker的配置broker.id0listererszookeeper.connectlog.dirslog.dir/tmp/kafka-logsnum.recovery.threads.per.data.dir1auto.create.topics.enabletrueauto.leader.rebalance.enabletrue, leader.imbalance.check.interval.seconds300, leader.imbalance…...

代码随想录第五十二天——最长递增子序列,最长连续递增序列,最长重复子数组
leetcode 300. 最长递增子序列 题目链接:最长递增子序列 dp数组及下标的含义 dp[i]表示i之前包括i的以nums[i]结尾的最长递增子序列的长度递推公式 位置i的最长升序子序列等于j从0到i-1各个位置的最长升序子序列 1 的最大值 所以if (nums[i] > nums[j]) dp[i]…...
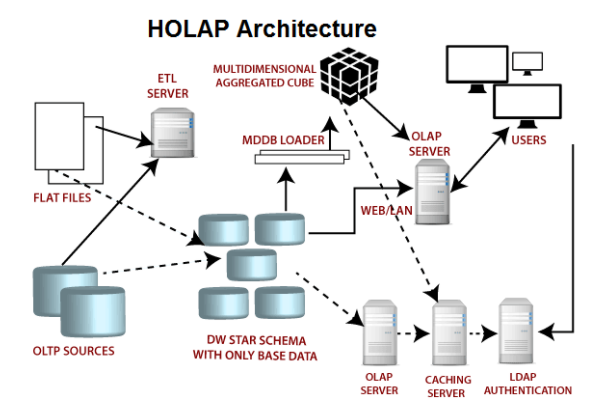
【大数据架构】OLAP实时分析引擎选型
OLAP引擎面临的挑战 常见OLAP引擎对比 OLAP分析场景中,一般认为QPS达到1000就算高并发,而不是像电商、抢红包等业务场景中,10W以上才算高并发,毕竟数据分析场景,数据海量,计算复杂,QPS能够达到1…...
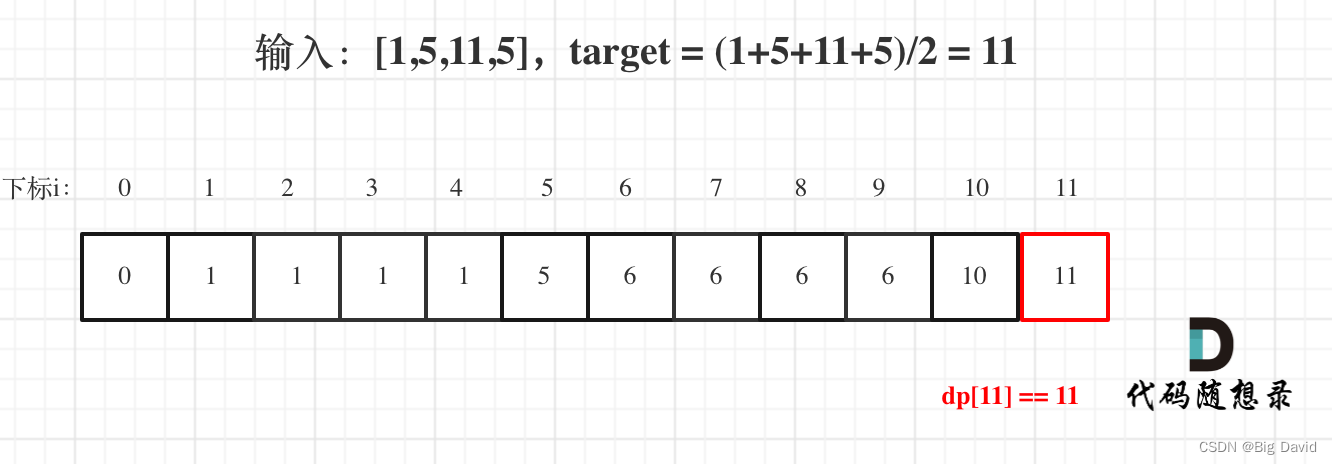
代码随想录刷题题Day29
刷题的第二十九天,希望自己能够不断坚持下去,迎来蜕变。😀😀😀 刷题语言:C Day29 任务 ● 01背包问题,你该了解这些! ● 01背包问题,你该了解这些! 滚动数组 …...
CVE-2023-51385 OpenSSH ProxyCommand命令注入漏洞
一、背景介绍 ProxyCommand 是 OpenSSH ssh_config 文件中的一个配置选项,它允许通过代理服务器建立 SSH 连接,从而在没有直接网络访问权限的情况下访问目标服务器。这对于需要经过跳板机、堡垒机或代理服务器才能访问的目标主机非常有用。 二、漏洞简…...

如何寻找到相对完整的真正的游戏的源码 用来学习?
在游戏开发的学习之路上,理论与实践是并重的两个方面。对于许多热衷于游戏开发的学习者来说,能够接触到真实的、完整的游戏源码无疑是一个极好的学习机会。但问题来了:我们该如何寻找到这些珍贵的资源呢? 开源游戏项目 GitHub:地…...
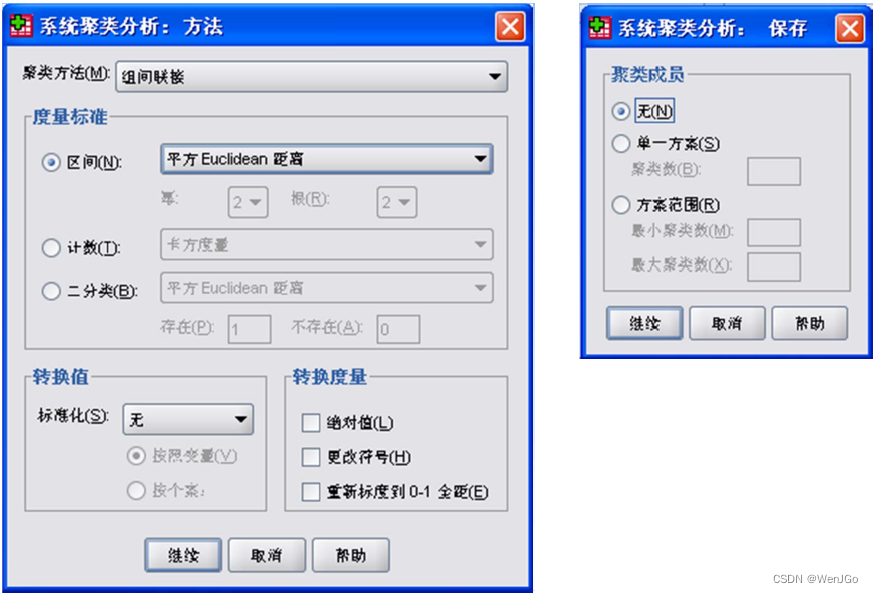
数模学习day11-系统聚类法
本文参考辽宁石油化工大学于晶贤教授的演示文档聚类分析之系统聚类法及其SPSS实现。 目录 1.样品与样品间的距离 2.指标和指标间的“距离” 相关系数 夹角余弦 3.类与类间的距离 (1)类间距离 (2)类间距离定义方式 1.最短…...

SpringBoot+Redis实现接口防刷功能
场景描述: 在实际开发中,当前端请求后台时,如果后端处理比较慢,但是用户是不知情的,此时后端仍在处理,但是前端用户以为没点到,那么再次点击又发起请求,就会导致在短时间内有很多请求…...

TensorRT加速推理入门-1:Pytorch转ONNX
这篇文章,用于记录将TransReID的pytorch模型转换为onnx的学习过程,期间参考和学习了许多大佬编写的博客,在参考文章这一章节中都已列出,非常感谢。 1. 在pytorch下使用ONNX主要步骤 1.1. 环境准备 安装onnxruntime包 安装教程可…...

springboot常用扩展点
当涉及到Spring Boot的扩展和自定义时,Spring Boot提供了一些扩展点,使开发人员可以根据自己的需求轻松地扩展和定制Spring Boot的行为。本篇博客将介绍几个常用的Spring Boot扩展点,并提供相应的代码示例。 1. 自定义Starter(面试常问) Sp…...
19道ElasticSearch面试题(很全)
点击下载《19道ElasticSearch面试题(很全)》 1. elasticsearch的一些调优手段 1、设计阶段调优 (1)根据业务增量需求,采取基于日期模板创建索引,通过 roll over API 滚动索引; (…...

向爬虫而生---Redis 拓宽篇3 <GEO模块>
前言: 继上一章: 向爬虫而生---Redis 拓宽篇2 <Pub/Sub发布订阅>-CSDN博客 这一章的用处其实不是特别大,主要是针对一些地图和距离业务的;就是Redis的GEO模块。 GEO模块是Redis提供的一种高效的地理位置数据管理方案,它允许我们存储和查询…...

Vue项目里实现json对象转formData数据
平常调用后端接口传参都是json对象,当提交表单遇到有附件需要传递时,通常是把附件上传单独做个接口,也有遇到后端让提交接口一并把附件传递到后端,这种情况需要把参数转成formData的数据,需要用到new FormData()。json…...

leetcode刷题记录
栈 2696. 删除子串后的字符串最小长度 哈希表 1. 两数之和 用map来保存每个数和他的索引 383. 赎金信 用map来存储字符的个数 链表 2. 两数相加 指针的移动 动态规划 53. 最大子数组和 2707. 字符串中的额外字符 递归 101. 对称二叉树 数学 1276. 不浪费原料的汉堡…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

云安全与网络安全:核心区别与协同作用解析
在数字化转型的浪潮中,云安全与网络安全作为信息安全的两大支柱,常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异,并探讨它们的协同作用。 一、核心区别 定义与范围 网络安全:聚焦于保…...

《Offer来了:Java面试核心知识点精讲》大纲
文章目录 一、《Offer来了:Java面试核心知识点精讲》的典型大纲框架Java基础并发编程JVM原理数据库与缓存分布式架构系统设计二、《Offer来了:Java面试核心知识点精讲(原理篇)》技术文章大纲核心主题:Java基础原理与面试高频考点Java虚拟机(JVM)原理Java并发编程原理Jav…...

轻量级Docker管理工具Docker Switchboard
简介 什么是 Docker Switchboard ? Docker Switchboard 是一个轻量级的 Web 应用程序,用于管理 Docker 容器。它提供了一个干净、用户友好的界面来启动、停止和监控主机上运行的容器,使其成为本地开发、家庭实验室或小型服务器设置的理想选择…...

Python爬虫(52)Scrapy-Redis分布式爬虫架构实战:IP代理池深度集成与跨地域数据采集
目录 一、引言:当爬虫遭遇"地域封锁"二、背景解析:分布式爬虫的两大技术挑战1. 传统Scrapy架构的局限性2. 地域限制的三种典型表现 三、架构设计:Scrapy-Redis 代理池的协同机制1. 分布式架构拓扑图2. 核心组件协同流程 四、技术实…...

关于 ffmpeg设置摄像头报错“Could not set video options” 的解决方法
若该文为原创文章,转载请注明原文出处 本文章博客地址:https://hpzwl.blog.csdn.net/article/details/148515355 长沙红胖子Qt(长沙创微智科)博文大全:开发技术集合(包含Qt实用技术、树莓派、三维、OpenCV…...
