[足式机器人]Part2 Dr. CAN学习笔记 - Ch02动态系统建模与分析
本文仅供学习使用
本文参考:
B站:DR_CAN
Dr. CAN学习笔记 - Ch02动态系统建模与分析
- 1. 课程介绍
- 2. 电路系统建模、基尔霍夫定律
- 3. 流体系统建模
- 4. 拉普拉斯变换(Laplace)传递函数、微分方程
- 4.1 Laplace Transform 拉式变换
- 4.2 收敛域(ROC)与逆变换(ILT)
- 4.3 传递函数 Transfer Function
- 5. 一阶系统的单位阶跃响应(step response),时间常数(Time Constant)
- 6. 频率响应与滤波器
- 7. 二阶系统
- 7.1 二阶系统对初始条件的动态响应 Matlab/Simulink - 2nd Order Syetem Response to IC
- 7.2 二阶系统的单位阶跃响应 2nd Order System Unit Step Response
- 7.3 二阶系统单位阶跃的性能分析与比较 2nd Order System Unit Step Response
- 7.4 共振现象-二阶系统频率响应,现象部分
- 7.5 二阶系统的频率响应
- 8. 二阶系统的频率响应
1. 课程介绍

2. 电路系统建模、基尔霍夫定律
基本元件:
电量 库伦( C C C) q q q
电流 安培( A A A) i i i —— i = d e d t i=\frac{\mathrm{d}e}{\mathrm{d}t} i=dtde 流速
电压 伏特( V V V) e e e
电阻 欧姆( Ω \varOmega Ω) R R R —— e R = i R e_{\mathrm{R}}=iR eR=iR
电容 法拉( F F F) C C C —— q = C e C , e C = 1 C q = 1 C ∫ 0 t i d t q=Ce_{\mathrm{C}},e_{\mathrm{C}}=\frac{1}{C}q=\frac{1}{C}\int_0^t{i}\mathrm{d}t q=CeC,eC=C1q=C1∫0tidt
电感 亨利( H H H) L L L —— e L = L d i d t = L i ′ e_{\mathrm{L}}=L\frac{\mathrm{d}i}{\mathrm{d}t}=Li^{\prime} eL=Ldtdi=Li′

基尔霍夫定律
K(Kirchhoff) C(Current) L(Law) —— 所有进入某节点的电流的总和等于所有离开这个节点的的电流总和
K(Kirchhoff) V(Voltage) L(Law) —— 沿着闭合回路所有元件两端的电压的代数和等于零

 )
)
3. 流体系统建模

流量 flow rate q q q m 3 / s m^3/s m3/s
体积 volume V V V m 3 m^3 m3
高度 heigh h h h m m m
压强 pressure p p p N / m ( p a s c a l ) N/m\left( pascal \right) N/m(pascal)
静压 Hydrostatic Pressure p H y d r o = F H y d r o A = m g A = ρ g h p_{\mathrm{Hydro}}=\frac{F_{\mathrm{Hydro}}}{A}=\frac{mg}{A}=\rho gh pHydro=AFHydro=Amg=ρgh
绝对压强 Asolute Pressure p a b s = p a + p H y d r o = p a + ρ g h p_{abs}=p_{\mathrm{a}}+p_{\mathrm{Hydro}}=p_{\mathrm{a}}+\rho gh pabs=pa+pHydro=pa+ρgh
表压 Gauge Pressure P g a u g e = p a b s − p a = ρ g h P_{\mathrm{gauge}}=p_{abs}-p_{\mathrm{a}}=\rho gh Pgauge=pabs−pa=ρgh
流阻 Fluid Resistance

质量守恒 Conservation of Mass

4. 拉普拉斯变换(Laplace)传递函数、微分方程
4.1 Laplace Transform 拉式变换
f ( t ) → F ( s ) f\left( t \right) \rightarrow F\left( s \right) f(t)→F(s) : 时域 - 频域 s = σ + j w s=\sigma +jw s=σ+jw





4.2 收敛域(ROC)与逆变换(ILT)


微分方程——描述动态世界
状态变量 : d x ⃗ d t \frac{\mathrm{d}\vec{x}}{\mathrm{d}t} dtdx-时间
位移: s s s , 速度: d x d t \frac{\mathrm{d}x}{\mathrm{d}t} dtdx ,加速度: d 2 x d t 2 \frac{\mathrm{d}^2x}{\mathrm{d}t^2} dt2d2x
- F = m d 2 x d t 2 F=m\frac{\mathrm{d}^2x}{\mathrm{d}t^2} F=mdt2d2x
- d T d t = − k ( T − C ) \frac{\mathrm{d}T}{\mathrm{d}t}=-k\left( T-C \right) dtdT=−k(T−C)
- d P d t = − r p ( 1 − p k ) \frac{\mathrm{d}P}{\mathrm{d}t}=-rp\left( 1-\frac{p}{k} \right) dtdP=−rp(1−kp) 人口增长
常系数线性 —— 线性时不变系统
- 求解 3Step
从 t t t— s s s L [ f ( t ) ] \mathcal{L} \left[ f\left( t \right) \right] L[f(t)]
运算求解
从 s s s— t t t L − 1 [ F ( s ) ] \mathcal{L} ^{-1}\left[ F\left( s \right) \right] L−1[F(s)]
非线性
- 线性化
- 非线性分析控制

4.3 传递函数 Transfer Function
——根轨迹 BodePlot 信号处理


5. 一阶系统的单位阶跃响应(step response),时间常数(Time Constant)

换个角度分析单位阶跃响应(System Unit Step Response - 一阶 1st order)——LTI
一阶线性时不变 —— 1st order LTI
x ˙ + a x = a u x ( 0 ) = x ˙ ( 0 ) = 0 \dot{x}+ax=au \\ x\left( 0 \right) =\dot{x}\left( 0 \right) =0 x˙+ax=aux(0)=x˙(0)=0
传递函数 : s X ( s ) + a X ( s ) = a U ( s ) ; H ( s ) = X ( s ) U ( s ) = a s + a sX\left( s \right) +aX\left( s \right) =aU\left( s \right) ;H\left( s \right) =\frac{X\left( s \right)}{U\left( s \right)}=\frac{a}{s+a} sX(s)+aX(s)=aU(s);H(s)=U(s)X(s)=s+aa

Another Viewpoint : x ˙ + a x = a u , t ⩾ 0 , u = 1 ⇒ x ˙ = a − a x = a ( 1 − x ) \dot{x}+ax=au,t\geqslant 0,u=1\Rightarrow \dot{x}=a-ax=a\left( 1-x \right) x˙+ax=au,t⩾0,u=1⇒x˙=a−ax=a(1−x)

6. 频率响应与滤波器




1st order system 一阶系统

低通滤波器——Loss Pass Filter

7. 二阶系统
7.1 二阶系统对初始条件的动态响应 Matlab/Simulink - 2nd Order Syetem Response to IC
Vibration 振动



7.2 二阶系统的单位阶跃响应 2nd Order System Unit Step Response

Unit Step Imput 单位阶跃


7.3 二阶系统单位阶跃的性能分析与比较 2nd Order System Unit Step Response


7.4 共振现象-二阶系统频率响应,现象部分

7.5 二阶系统的频率响应

8. 二阶系统的频率响应

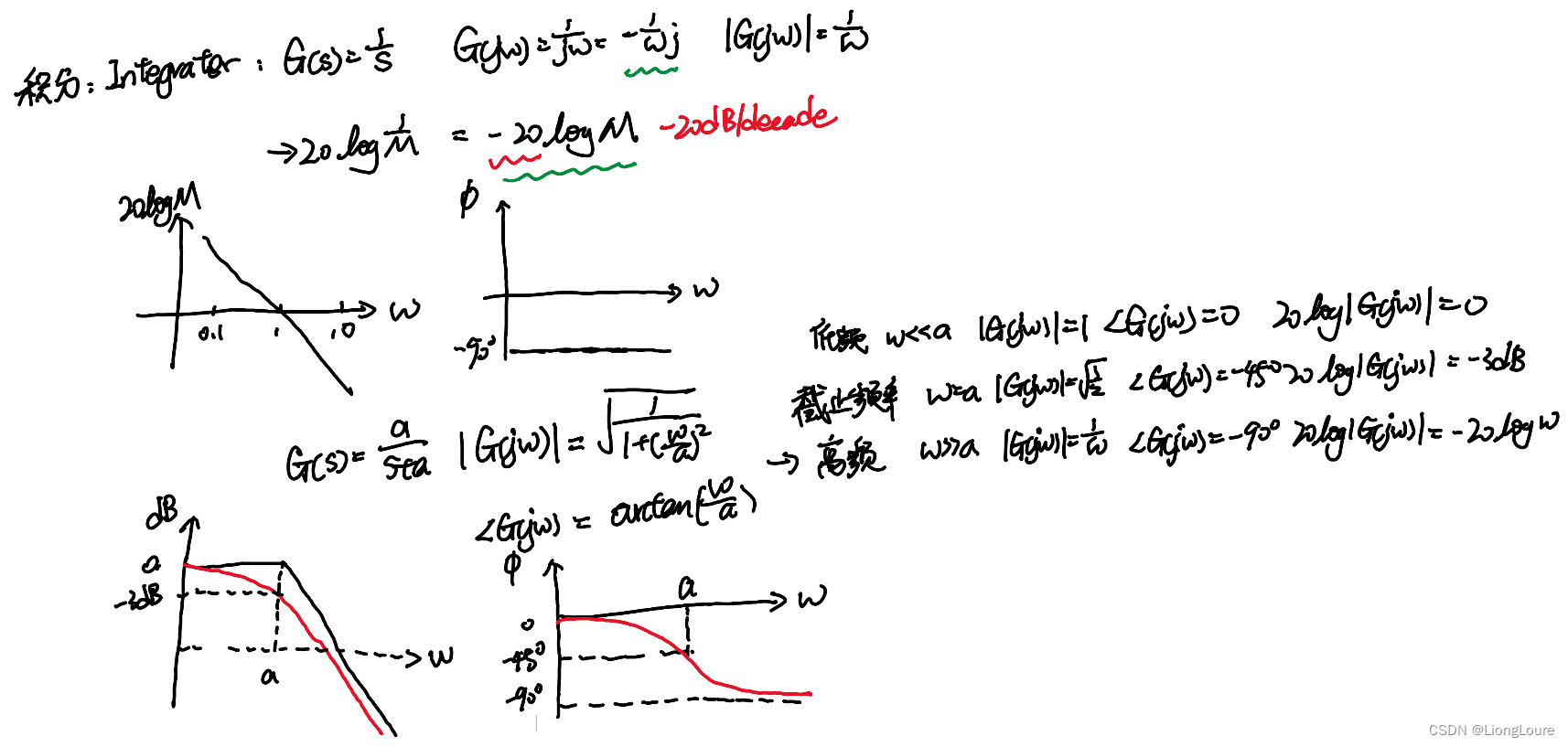
Bode Plot 手绘技巧与应用


相关文章:

[足式机器人]Part2 Dr. CAN学习笔记 - Ch02动态系统建模与分析
本文仅供学习使用 本文参考: B站:DR_CAN Dr. CAN学习笔记 - Ch02动态系统建模与分析 1. 课程介绍2. 电路系统建模、基尔霍夫定律3. 流体系统建模4. 拉普拉斯变换(Laplace)传递函数、微分方程4.1 Laplace Transform 拉式变换4.2 收…...

【一周年创作总结】人生是远方的无尽旷野呀
那一眼瞥见的伟大的灵魂,却似模糊的你和我 文章目录 📒各个阶段的experience🔎大一寒假🔎大一下学期🔎大一暑假🔎大二上学期(现在) 🍔相遇CSDN🛸自媒体&#…...

金融帝国实验室(Capitalism Lab)V10版本游戏平衡性优化与改进
即将推出的V10版本中的各种游戏平衡性优化与改进: ————————————— 一、当玩家被提议收购一家即将破产的公司时,显示商业秘密。 当一家公司濒临破产,玩家被提议收购该公司时,如果玩家有兴趣评估该公司,则无…...

[SpringBoot]接口的多实现:选择性注入SpringBoot接口的实现类
最近在项目中遇到两种情况,准备写个博客记录一下。 情况说明:Service层一个接口是否可以存在多个具体实现,此时应该如何调用Service(的具体实现)? 其实之前的项目中也遇到过这种情况,只不过我采…...

北京大学 wlw机器学习2022春季期末试题分析
北京大学 wlw机器学习2022春季期末试题分析 前言新的开始第一题第二题第三题 前言 你好! 这是你第一次使用 Markdown编辑器 所展示的欢迎页。如果你想学习如何使用Markdown编辑器, 可以仔细阅读这篇文章,了解一下Markdown的基本语法知识。 新的开始 第…...
)
前端文件下载方法(包含get和post)
export const downloadFileWithIframe (url, name) > {const iframe document.createElement(iframe);iframe.style.display none; // 防止影响页面iframe.style.height 0; // 防止影响页面iframe.name name;iframe.src url;document.body.appendChild(iframe); // 这…...
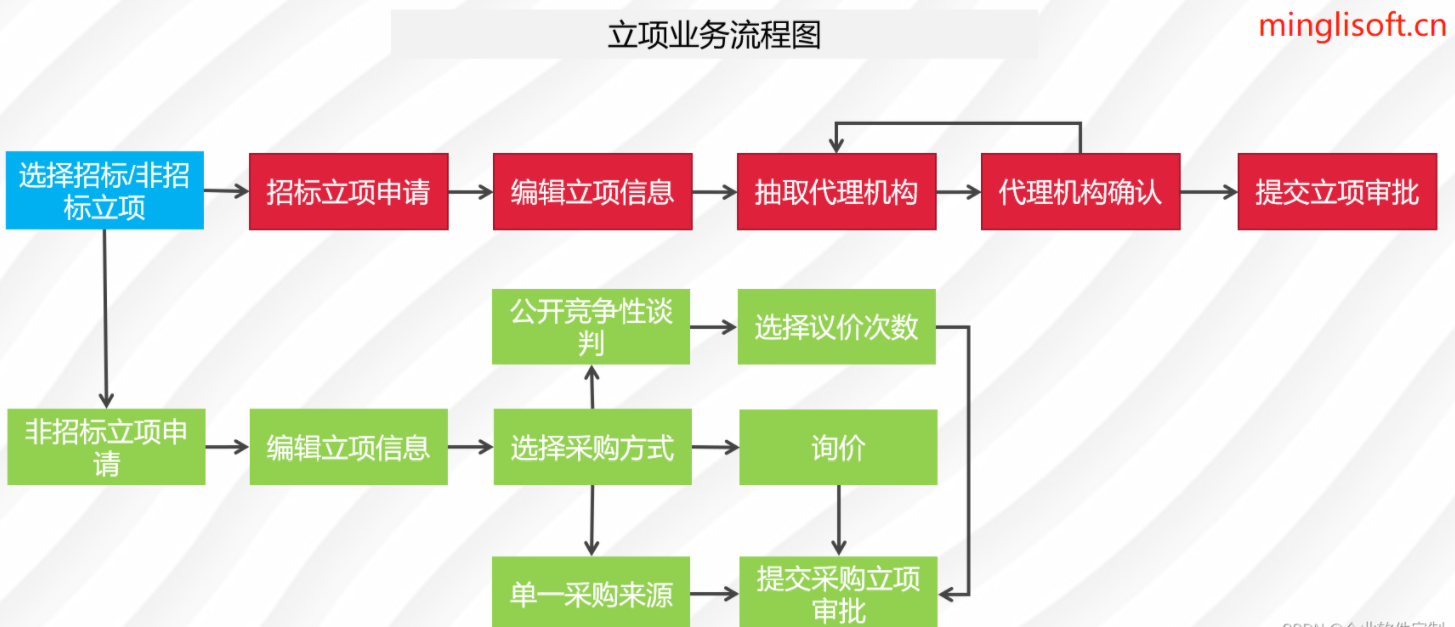
高性能、可扩展、支持二次开发的企业电子招标采购系统源码
在数字化时代,企业需要借助先进的数字化技术来提高工程管理效率和质量。招投标管理系统作为企业内部业务项目管理的重要应用平台,涵盖了门户管理、立项管理、采购项目管理、采购公告管理、考核管理、报表管理、评审管理、企业管理、采购管理和系统管理等…...

2645. 构造有效字符串的最少插入数
Problem: 2645. 构造有效字符串的最少插入数 文章目录 解题思路解决方法复杂度分析代码实现 解题思路 解决此问题需要确定如何以最小的插入次数构造一个有效的字符串。首先,我们需要确定开头的差距,然后决定中间的补足,最后决定末尾的差距。…...
C#,快速排序算法(Quick Sort)的非递归实现与数据可视化
排序算法是编程的基础。 常见的四种排序算法是:简单选择排序、冒泡排序、插入排序和快速排序。其中的快速排序的优势明显,一般使用递归方式实现,但遇到数据量大的情况则无法适用。实际工程中一般使用“非递归”方式实现。 快速排序(Quick Sor…...

【操作系统xv6】学习记录2 -RISC-V Architecture
说明:看完这节,不会让你称为汇编程序员,知识操作系统的前置。 ref:https://binhack.readthedocs.io/zh/latest/assembly/mips.html https://www.bilibili.com/video/BV1w94y1a7i8/?p7 MIPS MIPS的意思是 “无内部互锁流水级的微…...
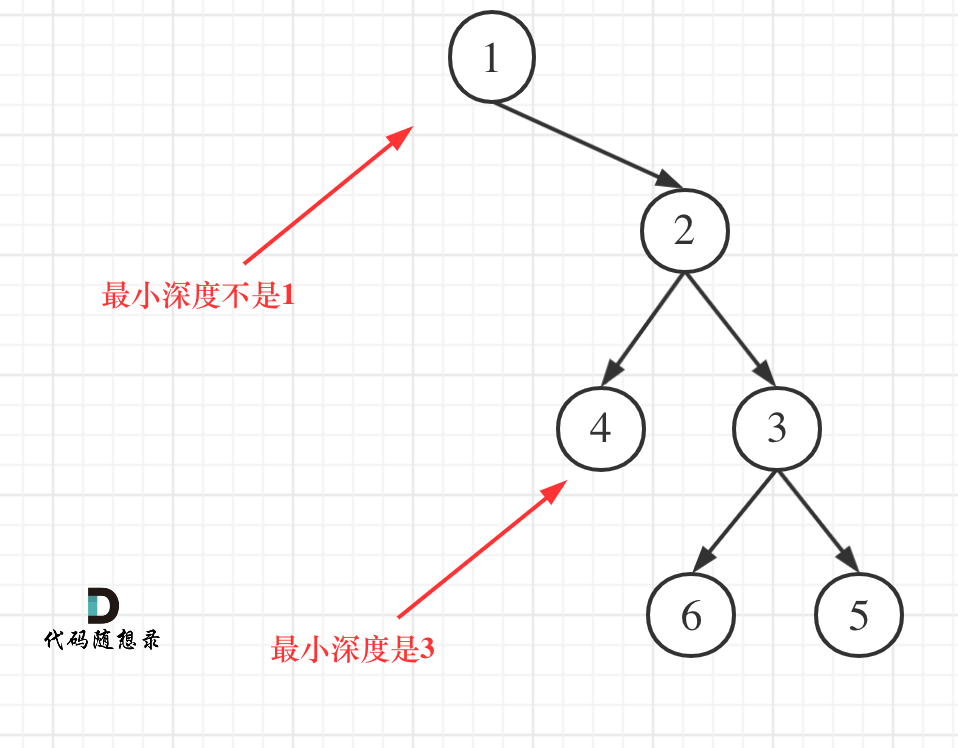
C++力扣题目111--二叉树的最小深度
力扣题目链接(opens new window) 给定一个二叉树,找出其最小深度。 最小深度是从根节点到最近叶子节点的最短路径上的节点数量。 说明: 叶子节点是指没有子节点的节点。 示例: 给定二叉树 [3,9,20,null,null,15,7], 返回它的最小深度 2 思路 看完了这篇104.二…...
)
【图像拼接】源码精读:Adaptive As-Natural-As-Possible Image Stitching(AANAP/ANAP)
第一次来请先看这篇文章:【图像拼接(Image Stitching)】关于【图像拼接论文源码精读】专栏的相关说明,包含专栏内文章结构说明、源码阅读顺序、培养代码能力、如何创新等(不定期更新) 【图像拼接论文源码精读】专栏文章目录 【源码精读】As-Projective-As-Possible Imag…...
解决docker run报错:Error response from daemon: No command specified.
将docker镜像export/import之后,对新的镜像执行docker run时报错: docker: Error response from daemon: No command specified. 解决方法: 方案1: 查看容器的command: docker ps --no-trunc 在docker run命令上增加…...

算法第十二天-最大整除子集
最大整除子集 题目要求 解题思路 来自[宫水三叶] 根据题意:对于符合要求的[整除子集]中的任意两个值,必然满足[较大数]是[较小数]的倍数 数据范围是 1 0 3 10^3 103,我们不可能采取获取所有子集,再检查子集是否合法的暴力搜解法…...

简单易懂的PyTorch 损失函数:优化机器学习模型的关键
目录 torch.nn子模块Loss Functions详解 nn.L1Loss 用途 用法 使用技巧 注意事项 代码示例 nn.MSELoss 用途 用法 使用技巧 注意事项 代码示例 nn.CrossEntropyLoss 用途 用法 使用技巧 注意事项 代码示例 使用类别索引 使用类别概率 nn.CTCLoss 用途 …...

Kubernetes/k8s的存储卷/数据卷
k8s的存储卷/数据卷 容器内的目录和宿主机的目录挂载 容器在系统上的生命周期是短暂的,delete,k8s用控制创建的pod,delete相当于重启,容器的状态也会回复到初始状态 一旦回到初始状态,所有的后天编辑的文件都会消失…...
【漏洞复现】锐捷RG-UAC统一上网行为管理系统信息泄露漏洞
Nx01 产品简介 锐捷网络成立于2000年1月,原名实达网络,2003年更名,自成立以来,一直扎根行业,深入场景进行解决方案设计和创新,并利用云计算、SDN、移动互联、大数据、物联网、AI等新技术为各行业用户提供场…...
)
Android - 串口通讯(SerialPort)
最早的博客Android 模拟串口通信过程_launch virtual serial port driver pro-CSDN博客里就是用过 Google 提供的 demo,最近想再写个其他的demo发现用起来有点麻烦,还需要导入其他 module,因此在网上找到了Android-SerialPort-API: https://g…...

如何使用設置靜態住宅IP
靜態住宅IP就是一種靜態的、分配給住宅用戶的IP地址。與動態IP地址不同,靜態住宅IP一旦分配給用戶,就會一直保持不變,除非ISP(Internet Service Provider,互聯網服務提供商)進行手動更改。那麼,…...
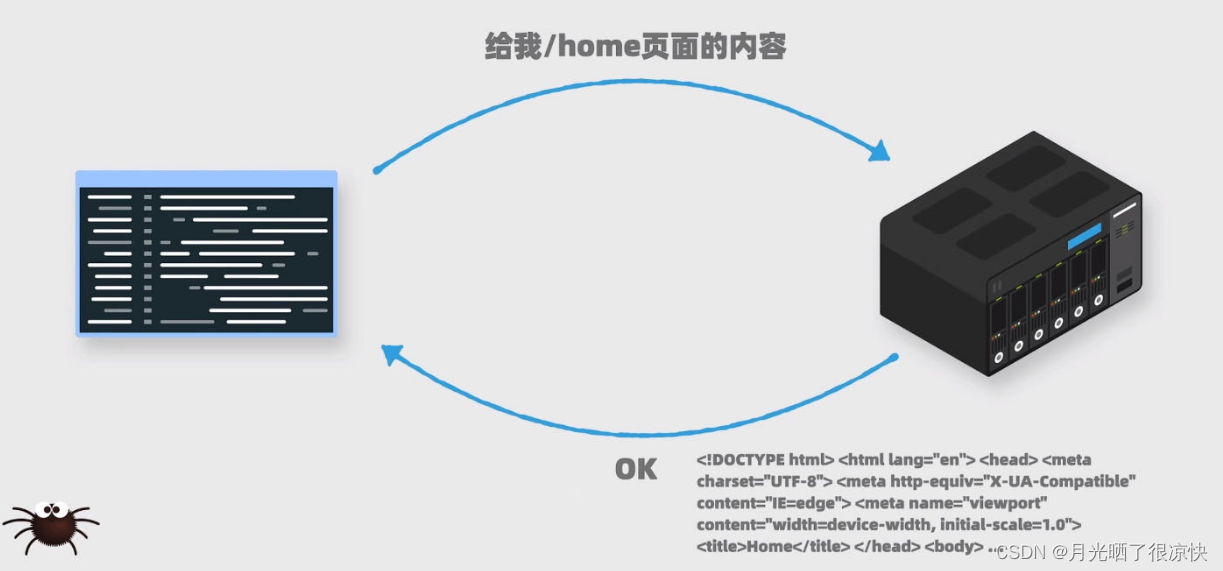
在学习爬虫前的准备
1. 写一个爬虫程序需要分几步 获取网页内容。 我们会通过代码给一个网站服务器发送请求,它会返回给我们网页上的内容。 在我们平时使用浏览器访问服务器内容是,本质上也是向服务器发送一个请求,然后服务器返回网页上的内容。只不过浏览器还会…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

sshd代码修改banner
sshd服务连接之后会收到字符串: SSH-2.0-OpenSSH_9.5 容易被hacker识别此服务为sshd服务。 是否可以通过修改此banner达到让人无法识别此服务的目的呢? 不能。因为这是写的SSH的协议中的。 也就是协议规定了banner必须这么写。 SSH- 开头,…...

验证redis数据结构
一、功能验证 1.验证redis的数据结构(如字符串、列表、哈希、集合、有序集合等)是否按照预期工作。 2、常见的数据结构验证方法: ①字符串(string) 测试基本操作 set、get、incr、decr 验证字符串的长度和内容是否正…...

【Java】Ajax 技术详解
文章目录 1. Filter 过滤器1.1 Filter 概述1.2 Filter 快速入门开发步骤:1.3 Filter 执行流程1.4 Filter 拦截路径配置1.5 过滤器链2. Listener 监听器2.1 Listener 概述2.2 ServletContextListener3. Ajax 技术3.1 Ajax 概述3.2 Ajax 快速入门服务端实现:客户端实现:4. Axi…...

spring boot使用HttpServletResponse实现sse后端流式输出消息
1.以前只是看过SSE的相关文章,没有具体实践,这次接入AI大模型使用到了流式输出,涉及到给前端流式返回,所以记录一下。 2.resp要设置为text/event-stream resp.setContentType("text/event-stream"); resp.setCharacter…...
