动态规划算法
1.应用场景-背包问题
背包问题:有一个背包,容量为 4 磅 , 现有如下物品
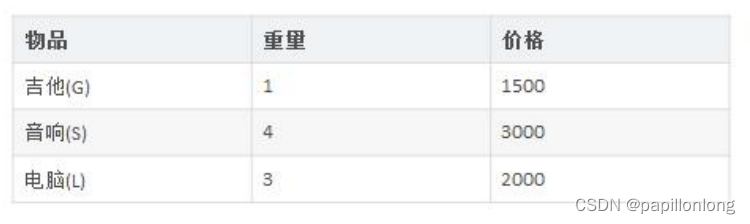
- 要求达到的目标为装入的背包的总价值最大,并且重量不超出
- 要求装入的物品不能重复
2.动态规划算法介绍
- 动态规划(Dynamic Programming)算法的核心思想是:将大问题划分为小问题进行解决,从而一步步获取最优解
的处理算法 - 动态规划算法与分治算法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这
些子问题的解得到原问题的解。 - 与分治法不同的是,适合于用动态规划求解的问题,经分解得到子问题往往不是互相独立的。 ( 即下一个子
阶段的求解是建立在上一个子阶段的解的基础上,进行进一步的求解 ) - 动态规划可以通过填表的方式来逐步推进,得到最优解.
3.动态规划算法最佳实践-背包问题
背包问题:有一个背包,容量为 4 磅 , 现有如下物品
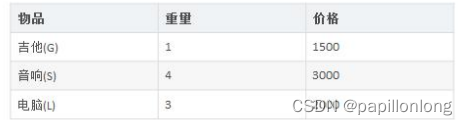
- 要求达到的目标为装入的背包的总价值最大,并且重量不超出
- 要求装入的物品不能重复
思路分析和图解
- 背包问题主要是指一个给定容量的背包、若干具有一定价值和重量的物品,如何选择物品放入背包使物品的价
值最大。其中又分 01 背包和完全背包(完全背包指的是:每种物品都有无限件可用) - 这里的问题属于 01 背包,即每个物品最多放一个。而无限背包可以转化为 01 背包。
- 算法的主要思想,利用动态规划来解决。每次遍历到的第 i 个物品,根据 w[i]和 v[i]来确定是否需要将该物品
放入背包中。即对于给定的 n 个物品,设 v[i]、w[i]分别为第 i 个物品的价值和重量,C 为背包的容量。再令 v[i][j]
表示在前 i 个物品中能够装入容量为 j 的背包中的最大价值。则我们有下面的结果
(1) v[i][0]=v[0][j]=0; //表示 填入表 第一行和第一列是 0
(2) 当 w[i]> j 时:v[i][j]=v[i-1][j] // 当准备加入新增的商品的容量大于 当前背包的容量时,就直接使用上一个
单元格的装入策略
(3) 当 j>=w[i]时: v[i][j]=max{v[i-1][j], v[i]+v[i-1][j-w[i]]}
// 当 准备加入的新增的商品的容量小于等于当前背包的容量, // 装入的方式:
v[i-1][j]: 就是上一个单元格的装入的最大值
v[i] : 表示当前商品的价值
v[i-1][j-w[i]] : 装入 i-1 商品,到剩余空间 j-w[i]的最大值
当 j>=w[i]时: v[i][j]=max{v[i-1][j], v[i]+v[i-1][j-w[i]]} :
- 图解的分析
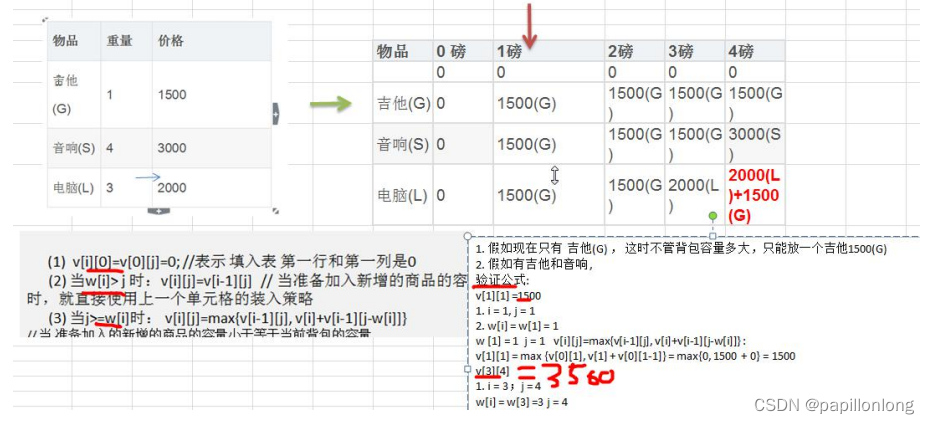
4.动态规划-背包问题的代码实现
public class KnapsackProblem {public static void main(String[] args) {// TODO Auto-generated method stubint[] w = { 1, 4, 3 };// 物品的重量int[] val = { 1500, 3000, 2000 };// 物品的价值 这里val[i] 就是前面讲的v[i]int m = 4;// 背包的容量int n = val.length;// 物品的个数// 创建二维数组// v[i][j]表示在前i个物品中能够装入容量为j的背包中的最大价值int[][] v = new int[n + 1][m + 1];// 初始化第一行和第一列,这里在本程序中,可以不去处理,因为默认就是0for (int i = 0; i < v.length; i++) {v[i][0] = 0;// 将第一列设置为0}for (int i = 0; i < v[0].length; i++) {v[0][i] = 0;// 将第一行设置0}// 根据前面得到的公式来动态规划处理for (int i = 1; i < v.length; i++) {// 不处理第一行 i是从1开始的for (int j = 1; j < v[0].length; j++) {// 不处理第一列,j是从1开始的// 公式if (w[i - 1] > j) {// 因为我们程序i是从1开始的,因此原来公式中的w[i]修改成w[i-1]v[i][j] = v[i - 1][j];} else {// 说明// 因为我们的i从1开始的,因此公式需要调整成// v[i][j]=Math.max(v[i-1][j],val[i-1]+v[i-1][j-w[i-1]]);v[i][j] = Math.max(v[i - 1][j], val[i - 1] + v[i - 1][j - w[i - 1]]);}}}// 输出一下v 看看目前情况for (int i = 0; i < v.length; i++) {for (int j = 0; j < v[i].length; j++) {System.out.print(v[i][j] + " ");}System.out.println();}}}
相关文章:

动态规划算法
1.应用场景-背包问题 背包问题:有一个背包,容量为 4 磅 , 现有如下物品 要求达到的目标为装入的背包的总价值最大,并且重量不超出要求装入的物品不能重复 2.动态规划算法介绍 动态规划(Dynamic Programming)算法的核心思想是&…...
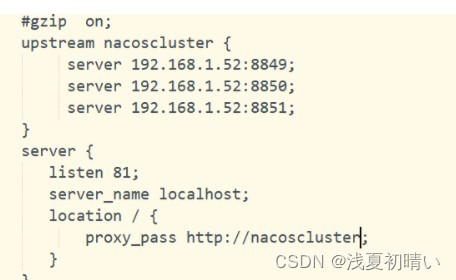
nacos的单机模式和集群模式
文章目录 目录 文章目录 前言 一、nacos数据库配置 二、单机模式 三、集群模式 四、使用nginx集群模式的负载均衡 总结 前言 一、nacos数据库配置 在数据库中创建nacos_config 编码格式utf8-mb4的数据库 把上面的数据库文件导入数据库 在 配置文件中添加如下 spring.datasour…...
Spring Boot 整合定时任务完成 从0 到1
Java 定时任务学习 定时任务概述 > 定时任务的应用场景非常广泛, 如果说 我们想要在某时某地去尝试的做某件事 就需要用到定时任务来通知我们 ,大家可以看下面例子 如果需要明天 早起,哪我们一般会去定一个闹钟去通知我们, 而在编程中 有许许多多的…...

Dialogue Transformers
Abstract 本文介绍了一种基于 Transformer 架构的 对话策略,其中自注意力机制被应用于对话轮次(dialogue turns)的序列上。近期的一些工作使用层次化的循环神经网络(hierarchical recurrent neural networks)在对话上下文中对多个话语(utterances)进行编码,但是我们认…...
【遇见青山】项目难点:缓存击穿问题解决方案
【遇见青山】项目难点:缓存击穿问题解决方案1.缓存击穿互斥锁🔒方案逻辑过期方案2.基于互斥锁方案的具体实现3.基于逻辑过期方案的具体实现1.缓存击穿 缓存击穿问题也叫热点Key问题,就是一个被高并发访问并且缓存重建业务较复杂的key突然失效…...
)
2023Flag具体实施计划(短期)
重新看了flag ,要做的事情太多,太杂,上周一周时间都在纠结和琢磨,该怎么下手。如何达成小目标。特别是沟通,汇报,演讲能力, 以及整体体系化的思维能力的训练。如何做到多思考,而不是瞎搞。这边重…...
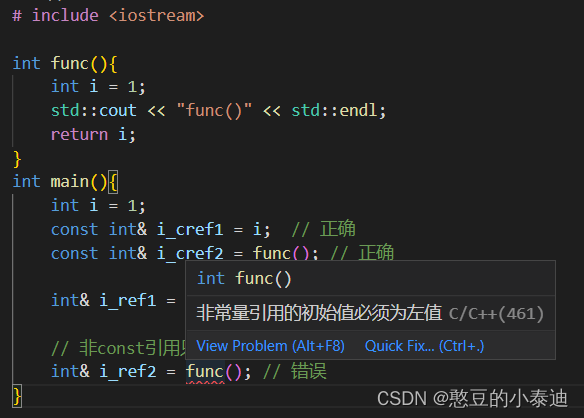
研一寒假C++复习笔记--左值和右值的理解和使用
目录 1--左值和右值的定义 2--简单理解左值和右值的代码 3--非const引用只能接受左值 1--左值和右值的定义 左值:L-Value,L理解为 Location,表示可寻; 右值:R-Value,R理解为 Read,表示可读&a…...

Android 11.0 动态修改SystemProperties中ro开头系统属性的值
需求: 在11.0的产品开发中,对于定制功能的需求很多,有些机型要求可以修改系统属性值,对于系统本身在10.0以后为了系统安全性,不允许修改ro开头的SystemProperties的值,所以如果要求修改ro的相关系统属性&am…...

为什么分库分表
系列文章目录 文章目录系列文章目录前言一、什么是分库分表二、分库分表的原因分库分表三、如何分库分表3.1 垂直拆分1.垂直分库2、垂直分表3.2 水平拆分水平分库水平分表水平分库分表的策略hash取模算法range范围rangehash取模混合地理位置分片预定义算法四、分库分表的问题分…...

1625_MIT 6.828 stabs文档信息整理_下
全部学习汇总: GreyZhang/g_unix: some basic learning about unix operating system. (github.com) 继续之前的学习笔记,整理一下最近看过的一点stabs资料。 这一页中有一半的信息是Fortran专用的,直接跳过。参数的符号修饰符是p,…...
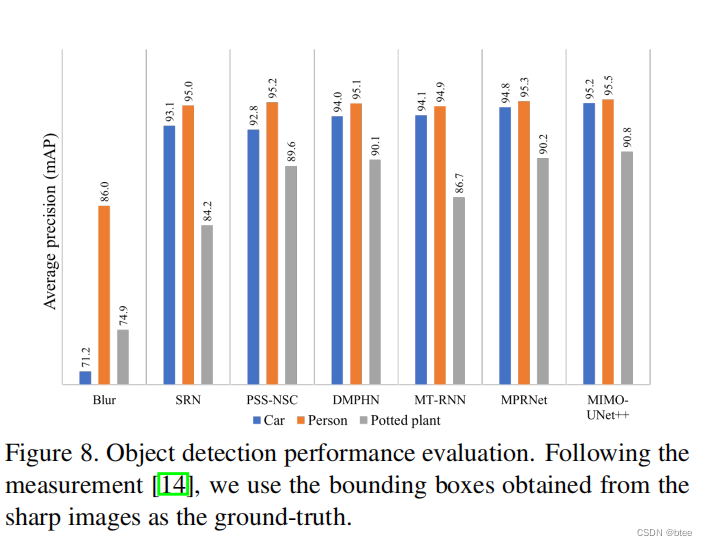
论文阅读 | Rethinking Coarse-to-Fine Approach in Single Image Deblurring
前言:ICCV2021图像单帧运动去糊论文 论文地址:【here】 代码地址:【here】 Rethinking Coarse-to-Fine Approach in Single Image Deblurring 引言 图像去糊来自与物体或相机的运动。现有的deblur领域的深度学习方法大多都是coarse-to-fin…...

Mysql 增删改查(二)—— 增(insert)、删(delete)、改(update)
目录 一、插入 1、insert 2、replace(插入否则更新) 二、更新(update) 三、删除 1、delete 2、truncate(截断表,慎用) 一、插入 1、insert (1) 单行 / 多行插入 全列插入:…...

JSD2212复习串讲
1. Java语言基础阶段 这一部分主要是练,给一些题目还有讲解一些最基础的语法,做一些额外的补充 1.1 基本概念 1.2 变量 1.2.1 数据类型 4类8种 基本类型:整形、浮点型、字符型、布尔型 整形:byte -》short-》int-》long 浮点…...

sphinx 升级到6.x后的Jquery问题
sphinx 升级到6.0 后,以前对于jquery的默认引用方式发生了改变以前在编译后的html中jquery是如下引用的:<script src"_static/jquery.js"></script>而升级到6.0后,对于jquery 是一个googleapi的远程jquery调用…...

NSSCTF Round#8 Basic
from:http://v2ish1yan.top MyDoor 使用php伪协议读取index.php的代码 php://filter/readconvert.base64-encode/resourceindex.php<?php error_reporting(0);if (isset($_GET[N_S.S])) {eval($_GET[N_S.S]); }if(!isset($_GET[file])) {header(Location:/index.php?fi…...

多传感器融合定位十二-基于图优化的建图方法其一
多传感器融合定位十二-基于图优化的建图方法其一1. 基于预积分的融合方案流程1.1 优化问题分析1.2 预积分的作用1.3 基于预积分的建图方案流程2. 预积分模型设计3. 预积分在优化中的使用3.1 使用方法3.2 残差设计3.3 残差雅可比的推导3.3.1 姿态残差的雅可比3.3.2 速度残差的雅…...

RockChip MPP编码
概述瑞芯微提供的媒体处理软件平台(Media Process Platform,简称 MPP)是适用于瑞芯微芯片系列的通用媒体处理软件平台。该平台对应用软件屏蔽了芯片相关的复杂底层处理,其目的是为了屏蔽不同芯片的差异,为使用者提供统…...

【学习笔记】NOIP暴零赛2
细思极恐,我的能力已经退步到这个地步了吗? 数据结构 这题的修改是强行加进去迷惑你的。 考虑怎么求树的带权重心。 完了我只会树形dp 完了完了 结论:设uuu的子树和为szusz_uszu,所有点权值和为sss,那么树的带…...

linux基本功系列之hostname实战
文章目录前言一. hostname命令介绍二. 语法格式及常用选项三. 参考案例3.1 显示本机的主机名3.2 临时修改主机名3.3 显示短格式的主机名3.4 显示主机的ip地址四. 永久修改主机名4.1 centos6 修改主机名的方式4.2 centos7中修改主机名永久生效总结前言 大家好,又见面…...
Easy-Es框架实践测试整理 基于ElasticSearch的ORM框架
文章目录介绍(1)Elasticsearch java 客户端种类(2)优势和特性分析(3)性能、安全、拓展、社区(2)ES版本及SpringBoot版本说明索引处理(一)索引别名策略&#x…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...

相关类相关的可视化图像总结
目录 一、散点图 二、气泡图 三、相关图 四、热力图 五、二维密度图 六、多模态二维密度图 七、雷达图 八、桑基图 九、总结 一、散点图 特点 通过点的位置展示两个连续变量之间的关系,可直观判断线性相关、非线性相关或无相关关系,点的分布密…...
