代码随想录算法训练营day48 | 动态规划 121 买卖股票的最佳时机 122 买卖股票的最佳时机II
day48
- 121. 买卖股票的最佳时机
- 1.确定dp数组(dp table)以及下标的含义
- 2.确定递推公式
- 3.dp数组如何初始化
- 4.确定遍历顺序
- 5.举例推导dp数组
- 122.买卖股票的最佳时机II
121. 买卖股票的最佳时机
题目链接
解题思路:
动规五部曲分析如下:
1.确定dp数组(dp table)以及下标的含义
dp[i][0] 表示第i天持有股票所得最多现金 ,这里可能有同学疑惑,本题中只能买卖一次,持有股票之后哪还有现金呢?
其实一开始现金是0,那么加入第i天买入股票现金就是 -prices[i], 这是一个负数。
dp[i][1] 表示第i天不持有股票所得最多现金
注意这里说的是“持有”,“持有”不代表就是当天“买入”!也有可能是昨天就买入了,今天保持持有的状态
2.确定递推公式
如果第i天持有股票即dp[i][0], 那么可以由两个状态推出来
- 第i-1天就持有股票,那么就保持现状,所得现金就是昨天持有股票的所得现金 即:
dp[i - 1][0] - 第i天买入股票,所得现金就是买入今天的股票后所得现金即:
-prices[i]
那么dp[i][0]应该选所得现金最大的,所以dp[i][0] = max(dp[i - 1][0], -prices[i]);
如果第i天不持有股票即dp[i][1], 也可以由两个状态推出来
- 第i-1天就不持有股票,那么就保持现状,所得现金就是昨天不持有股票的所得现金 即:
dp[i - 1][1] - 第i天卖出股票,所得现金就是按照今天股票价格卖出后所得现金即:
prices[i] + dp[i - 1][0]
同样dp[i][1]取最大的,dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);
3.dp数组如何初始化
由递推公式 dp[i][0] = max(dp[i - 1][0], -prices[i]); 和 dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);可以看出
其基础都是要从dp[0][0]和dp[0][1]推导出来。
那么dp[0][0]表示第0天持有股票,此时的持有股票就一定是买入股票了,因为不可能有前一天推出来,所以dp[0][0] -= prices[0];
dp[0][1]表示第0天不持有股票,不持有股票那么现金就是0,所以dp[0][1] = 0;
4.确定遍历顺序
从递推公式可以看出dp[i]都是由dp[i - 1]推导出来的,那么一定是从前向后遍历。
5.举例推导dp数组
以示例1,输入:[7,1,5,3,6,4]为例,dp数组状态如下:
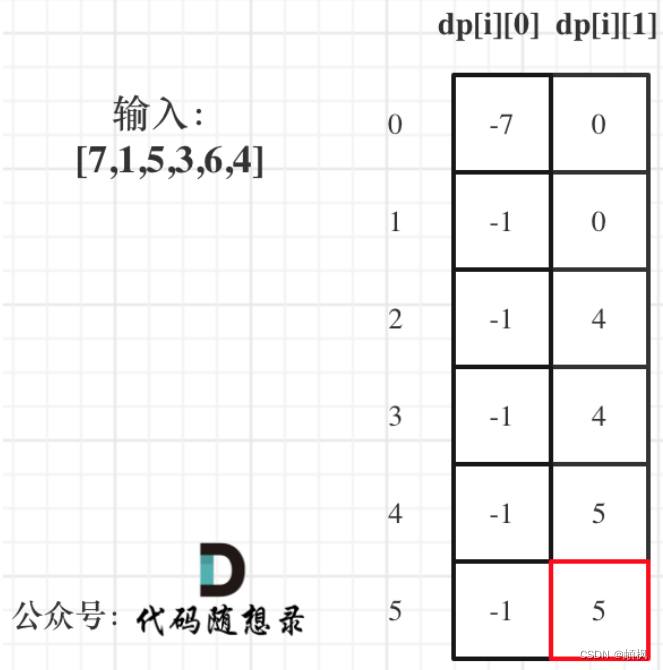
dp[5][1]就是最终结果。
为什么不是dp[5][0]呢?
因为本题中不持有股票状态所得金钱一定比持有股票状态得到的多!
以上分析完毕,C++代码如下:
class Solution {
public:int maxProfit(vector<int>& prices) {int len = prices.size();if (len == 0) return 0;vector<vector<int>> dp(len, vector<int>(2));dp[0][0] -= prices[0];dp[0][1] = 0;for (int i = 1; i < len; i++) {dp[i][0] = max(dp[i - 1][0], -prices[i]);dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);}return dp[len - 1][1];}
};
122.买卖股票的最佳时机II
题目链接
解题思路:
本题和121. 买卖股票的最佳时机 的唯一区别是本题股票可以买卖多次了(注意只有一只股票,所以再次购买前要出售掉之前的股票)
代码如下:
class Solution {
public:int maxProfit(vector<int>& prices) {int len = prices.size();vector<vector<int>> dp(len, vector<int>(2, 0));dp[0][0] -= prices[0];dp[0][1] = 0;for (int i = 1; i < len; i++) {dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]); // 注意这里是和121. 买卖股票的最佳时机唯一不同的地方。dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i]);}return dp[len - 1][1];}
};大家可以本题和121. 买卖股票的最佳时机的代码几乎一样,唯一的区别在:
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
这正是因为本题的股票可以买卖多次! 所以买入股票的时候,可能会有之前买卖的利润即:dp[i - 1][1],所以dp[i - 1][1] - prices[i]。
相关文章:

代码随想录算法训练营day48 | 动态规划 121 买卖股票的最佳时机 122 买卖股票的最佳时机II
day48121. 买卖股票的最佳时机1.确定dp数组(dp table)以及下标的含义2.确定递推公式3.dp数组如何初始化4.确定遍历顺序5.举例推导dp数组122.买卖股票的最佳时机II121. 买卖股票的最佳时机 题目链接 解题思路: 动规五部曲分析如下:…...

MediaTek 天玑 8000 5G移动平台详细参数
MediaTek 天玑 8000 移动平台 采用先进的 台积电 5nm 工艺,拥有出众的性能和能效,为高端智能手机用户提供出色的高帧率游戏和 5G 移动体验。 天玑 8000 采用了 MediaTek 诸多先进技术,内置 MediaTek Imagiq 780影像引擎、第五代 AI 处理器APU…...

Kafka
这里写目录标题1.Kafka1.1 Kafka概述1.2 kafka安装和配置1.3 入门案例1.4 kafka生产者详解1.4.1 生产者的参数1.Kafka 1.1 Kafka概述 Kafka 是一个分布式流媒体平台,类似于消息队列或企业消息传递系统。 producer:发布消息的对象称之为主题生产者(Ka…...
)
数据结构——第三章 栈与队列(2)
栈的运用1.括号匹配2.表达式求值2.1.算术表示式的形式2.2.后缀表达式求值2.3.将算术表达式转换为后缀表达式2.4.算术表达式直接求值3.栈与递归3.1.递归算法3.2.栈与函数调用3.3.递归工作与递归函数3.4.递归到非递归的转换1.括号匹配 void matching(char str[]) {//创建空栈Lin…...
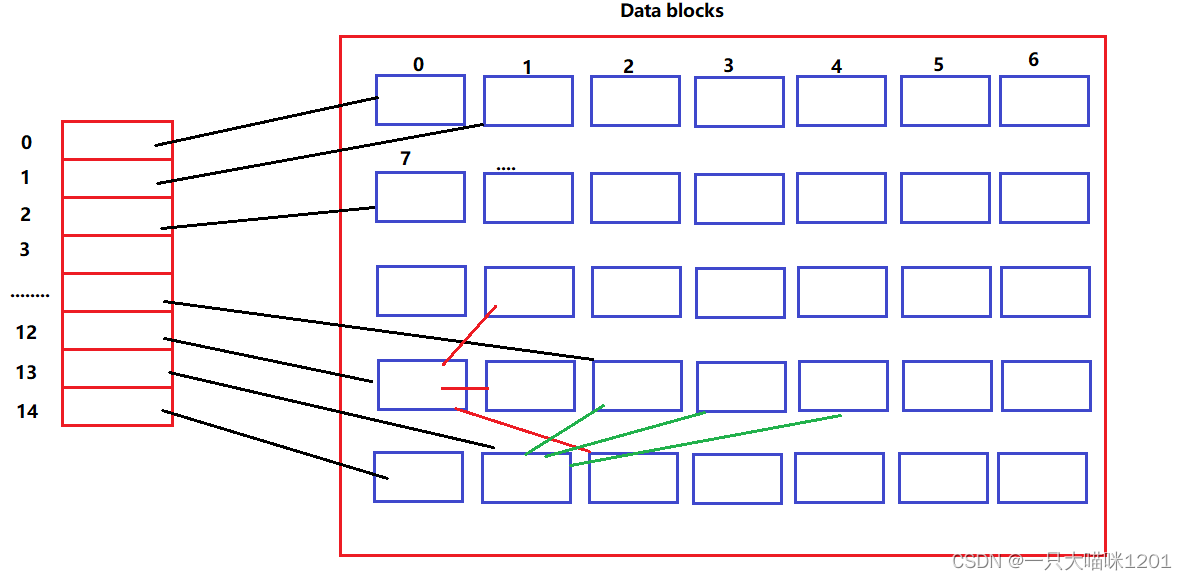
【Linux学习】基础IO——理解缓冲区 | 理解文件系统
🐱作者:一只大喵咪1201 🐱专栏:《Linux学习》 🔥格言:你只管努力,剩下的交给时间! 基础IO☕理解缓冲区🧃缓冲区的共识🧃缓冲区的位置🧃缓冲区的刷…...

RHCSA-重置root密码(3.3)
方法1:rd.break (1)首先重启系统,在此页面按e键,在屏幕上显示内核启动参数 (2)知道linux这行,末尾空格后输入rd.break,然后按ctrlx (3)查看&#…...
无公网IP快解析实现U+随时随地访问
现阶段商品从生产到消费者手中要经过多个环节,为实现对每一个环节进行管理,越来越多的企业选择通过信息化手段来实现。供应链管理系统配合供应链中各实体的业务需求,使操作流程和信息系统紧密配合,做到各环节无缝链接,…...

UVa 307 Sticks 木棍拼接 ID 迭代加深搜
题目链接:Sticks 题目描述: 小明一开始有一些长度相等的木棍,小明现在将木棍砍成了一些长度为整数的木棍,他现在忘记了最开始木棍的长度,你需要找到最短的可能木棍长度,例如给定5,2,1,5,2,1,5,2,15,2,1,5,2…...
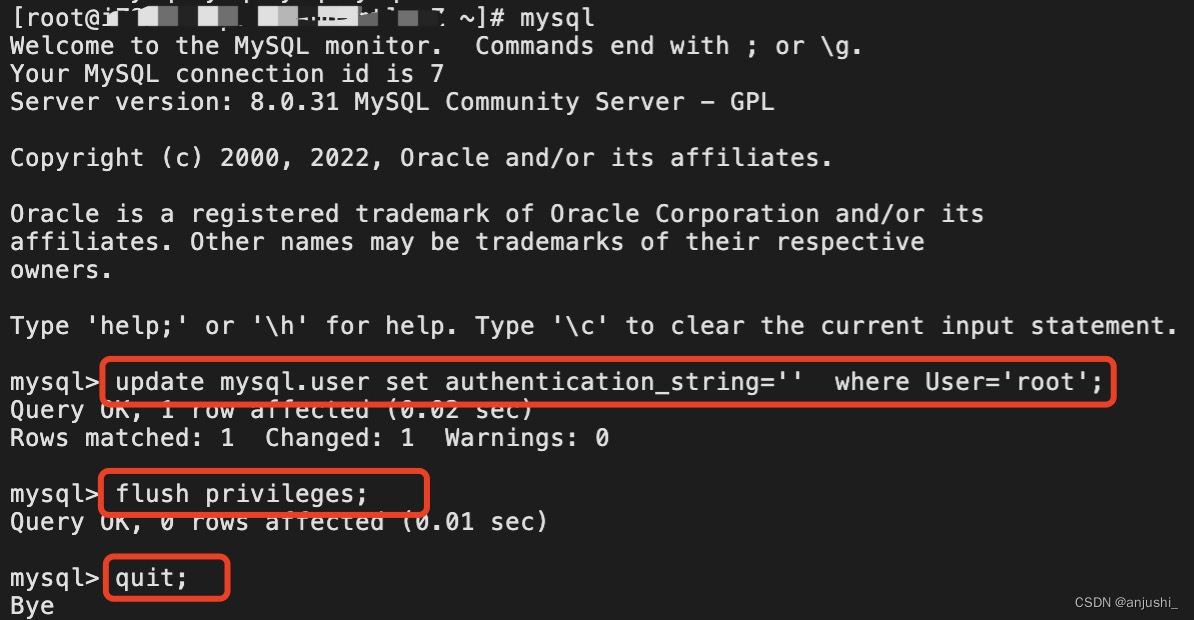
阿里云(CentOS)中MySQL8忘记密码的解决方法
阿里云(CentOS)中MySQL8忘记密码的解决方法 方法 在 skip-grant-tables 模式下启动 MySQL,该模式下启动 MySQL 时不启动授权表功能,可以直接免密码登录 实现 编辑 /etc/my.cnf 文件 vim /etc/my.cnf在 [mysqld] 区域末尾添加配置,设置免密…...
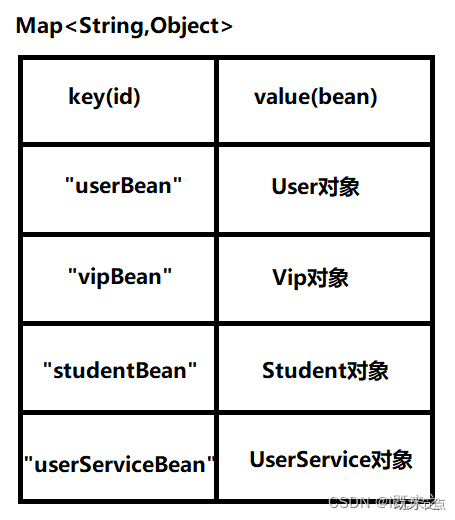
三、Spring的入门程序
第一个Spring程序 创建新的空工程spring6 设置JDK版本17,编译器版本17 设置IDEA的Maven:关联自己的maven 在空的工程spring6中创建第一个maven模块:spring6-001-first 在pom.xml添加spring context依赖和junit依赖, <?x…...
摘录一下Python列表和元组的学习笔记
1 基础概念 列表一个值,列表值指的是列表本身,而不是列表中的内容 列表用[]表示 列表中的内容称为 表项 len()函数可以显示列表中表项的个数,比如下面这个例子 spam [cat, bat, dog, rat]print(len(spam))列表的范围选取中,比…...

【量化金融】收益率、对数收益率、年华收益、波动率、夏普比率、索提诺比率、阿尔法和贝塔、最大回撤
【量化金融】收益率、对数收益率、年华收益、波动率、夏普比率、索提诺比率、阿尔法和贝塔、最大回撤 1 收益率 在学术界,建模一般不直接使用资产价格,而是使用资产收益率(Returns)。因为收益率比价格具有更好的统计特性,更便于建模。下经典…...
1_机器学习概述—全流程
文章目录1 机器学习定义2 机器学习常见应用框架(重点)3 机器学习分类3.1 监督学习(Supervised learning)3.2 无监督学习(Unsupervised learning)3.3 半监督学习(Semi-Supervised Learning&#…...

VUE中给对象添加新属性时,界面不刷新怎么办
一、直接添加属性的问题 举例: 定义一个p标签,通过v-for指令进行遍历 然后给botton标签绑定点击事件,我们预期点击按钮时,数据新增一个属性,界面也 新增一行。 <p v-for"(value,key) in item" :key&qu…...

视频号频出10w+,近期爆红的账号有哪些?
回顾2月,视频号持续放出大动作,不仅进行了16小时不间断的NBA全明星直播,还邀请国际奥委会入驻,分享奥运的最新资讯。视频号成为越来越多官方机构宣传推广的有效渠道。官方积极入驻,内容创作生态也在同步繁荣发展&#…...
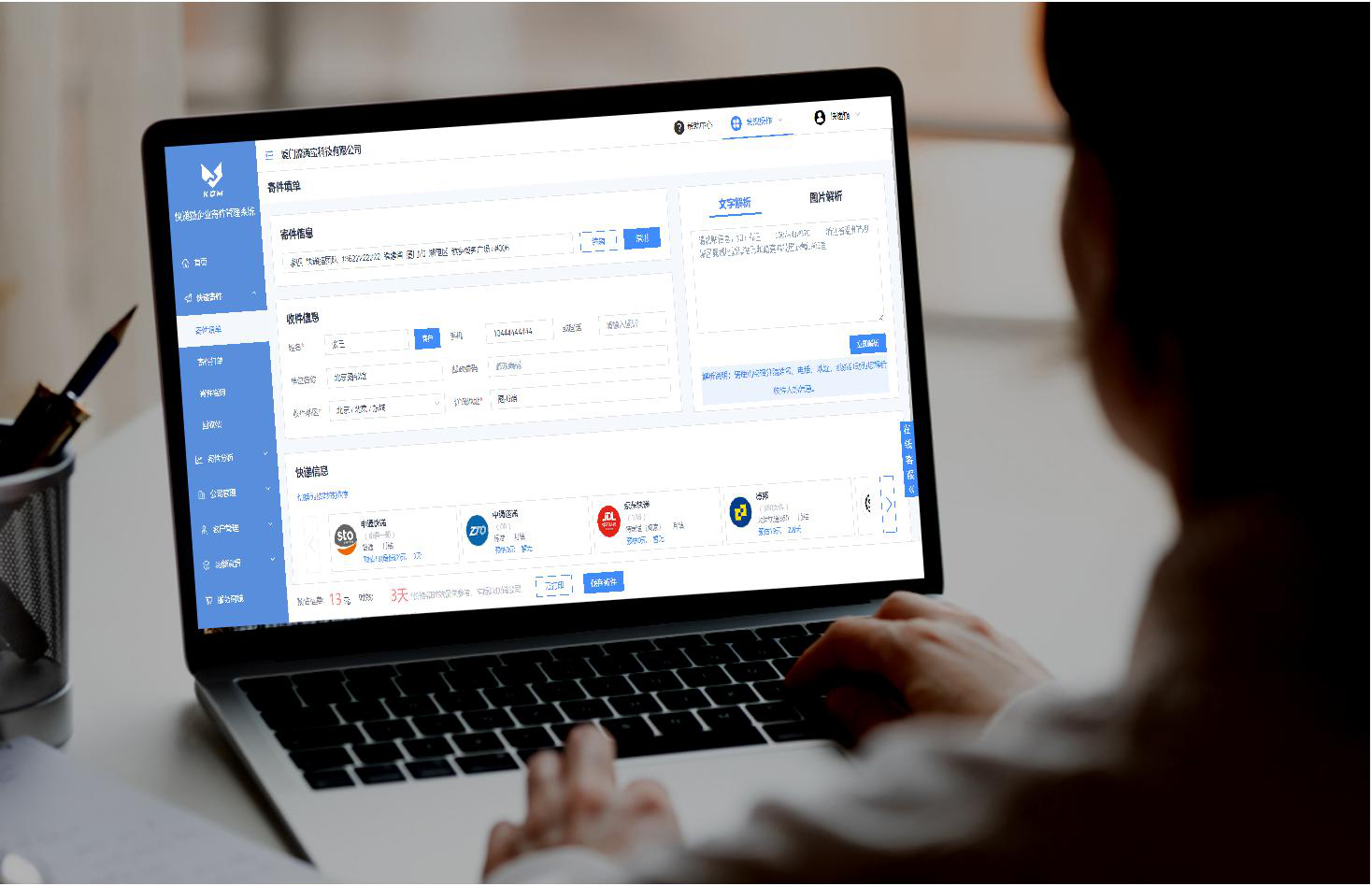
企业寄件现代化管理教程
现代化企业为了跟上时代发展的步伐,在不断完善着管理制度,其中公司寄件管理,也是重要的一个模块。为了提高公司快递的寄件效率,以及节约寄件成本,实现快递寄件的规范化,越来越多的现代化企业,开…...

django 在网页显示后台进度
1、定义函数打开网页 def PeformanceIndex(request): citys{‘wuhu’: ‘芜湖’, ‘xuancheng’: ‘宣城’, ‘tongling’: ‘铜陵’, ‘suzhou’: ‘宿州’, ‘maanshan’: ‘马鞍山’, ‘liuan’: ‘六安’, ‘huainan’: ‘淮南’, ‘huabei’: ‘淮北’, ‘hefei’: ‘合肥…...
)
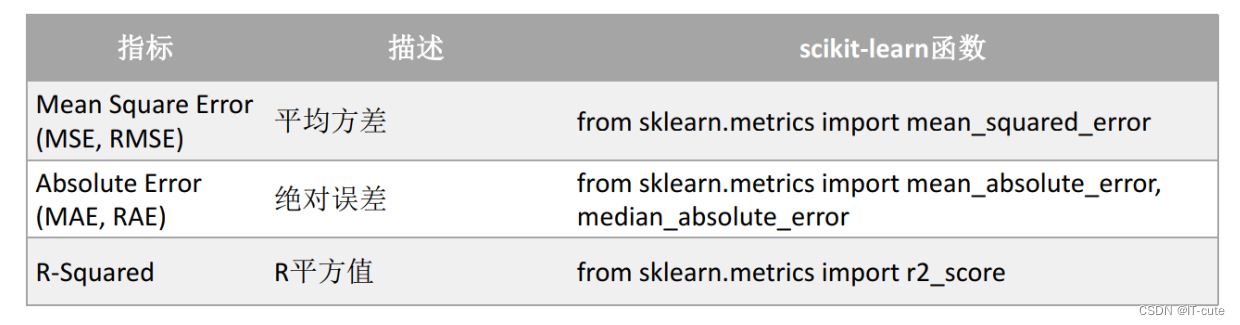
机器学习库(Numpy, Scikit-learn)
Numpy 创建数组 import numpy as npa np.array([1,2,3]) b np.array([(1.5,2,3), (4,5,6)], dtype float) c np.array([[(1.5,2,3), (4,5,6)], [(3,2,1), (4,5,6)]],dtype float)创建占位符 z1np.zeros((3,4)) z2np.ones((2,3,4),dtypenp.int16) z3d np.arange(10,25,5)…...

Linux操作系统学习(进程替换)
文章目录进程替换进程替换是什么?替换的方法进程替换简易shell模拟进程替换 进程替换是什么? 如下图所示: 进程替换就是,把进程B的代码和数据,替换正在执行的进程A的代码和数据在内存中的位置(若代码…...

【C++从入门到放弃】类和对象(中)———类的六大默认成员函数
🧑💻作者: 情话0.0 📝专栏:《C从入门到放弃》 👦个人简介:一名双非编程菜鸟,在这里分享自己的编程学习笔记,欢迎大家的指正与点赞,谢谢! 类和对…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...
