BP神经网络(公式推导+举例应用)
文章目录
- 引言
- M-P神经元模型
- 激活函数
- 多层前馈神经网络
- 误差逆传播算法
- 缓解过拟合化
- 结论
- 实验分析
引言
人工神经网络(Artificial Neural Networks,ANNs)作为一种模拟生物神经系统的计算模型,在模式识别、数据挖掘、图像处理等领域取得了显著的成功。其中,BP神经网络(Backpropagation Neural Network,BPNN)作为一种常见的前馈式神经网络,以其在模式学习和逼近函数方面的优越性受到广泛关注。BP神经网络不仅能够处理非线性关系,还能够通过训练不断调整网络参数,实现对复杂模型的逼近,具有较强的自适应性和泛化能力。
本文旨在深入探讨BP神经网络的基本原理和数学模型,通过对其公式的详细推导,为读者提供清晰的理论基础。此外,通过具体的举例应用,展示BP神经网络在实际问题中的有效性和应用前景。通过对BP神经网络的深入理解,我们可以更好地应用和优化该模型,推动人工智能领域的发展。
在神经网络研究的历史长河中,BP神经网络无疑是一个重要的里程碑,其不断演化和改进为解决实际问题提供了有力的工具。通过深入研究BP神经网络,我们有望更好地理解神经网络的内在机理,推动其在各个领域的广泛应用。在人工智能日益发展的今天,BP神经网络仍然是一个备受关注的研究方向,本文将为读者提供对其深入理解的途径和启发。
M-P神经元模型
在生物神经网络中,每个神经元与其他神经元相连接,当它“兴奋”时,就会向相连接的神经元发送化学物质,从而改变这些神经元内的电位;若某神经元的电位超过一个“阈值”,那么它就会被激活,即“兴奋”起来,向其他神经元发送化学物质。我们将上述所描述的情形抽象为下图所示(M-P神经元模型):
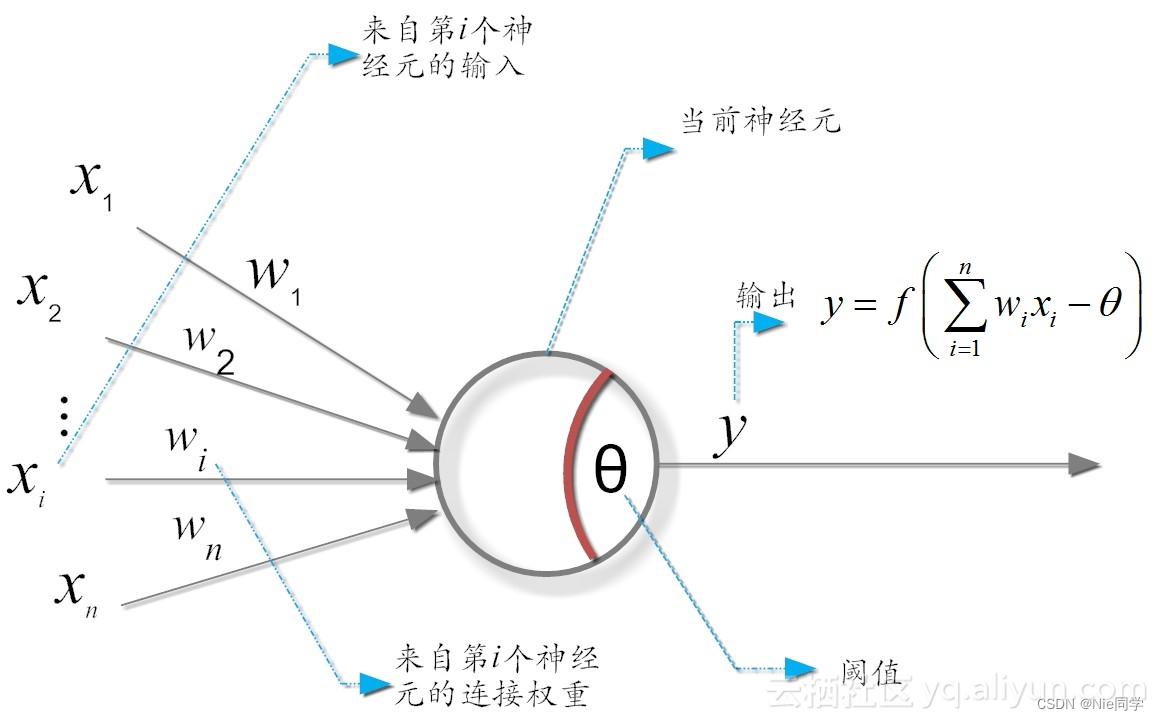
在这个模型中,神经元接受到来自 n n n个其他神经元传递过来的输入信号,这些输入信号通过带权的连接进行传递,神经元接受到的总输入值与神经元的阈值进行对比,然后通过”激活函数“处理以产生神经元的输出。
激活函数
理想中的激活函数如下图所示:
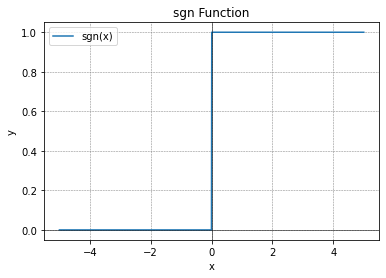
s g n ( x ) = { 1 , x ≥ 0 0 , x < 0 sgn(x)= \begin{cases} 1,\quad x\geq 0\\ 0, \quad x<0 \end{cases} sgn(x)={1,x≥00,x<0
显然“1”对应神经元兴奋、“0”对应神经元抑制。然而 s g n ( x ) sgn(x) sgn(x)数学性质不好,不具备连续性且不光滑。因此实际上我们采用 s i g m o i d sigmoid sigmoid函数作为激活函数,典型的 s i g m o i d sigmoid sigmoid函数如下图所示:
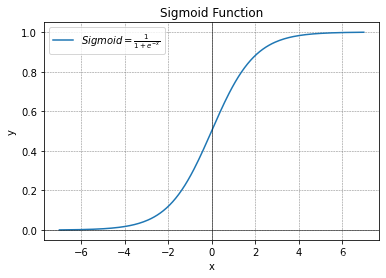
s i g m o i d ( x ) = 1 1 + e − x sigmoid(x)=\frac{1}{1+e^{-x}} sigmoid(x)=1+e−x1
然后将许多的神经元按一定的层次连接起来,就构成了一个神经网络。
多层前馈神经网络
常见的神经网络是形如下图所示的层级结构:
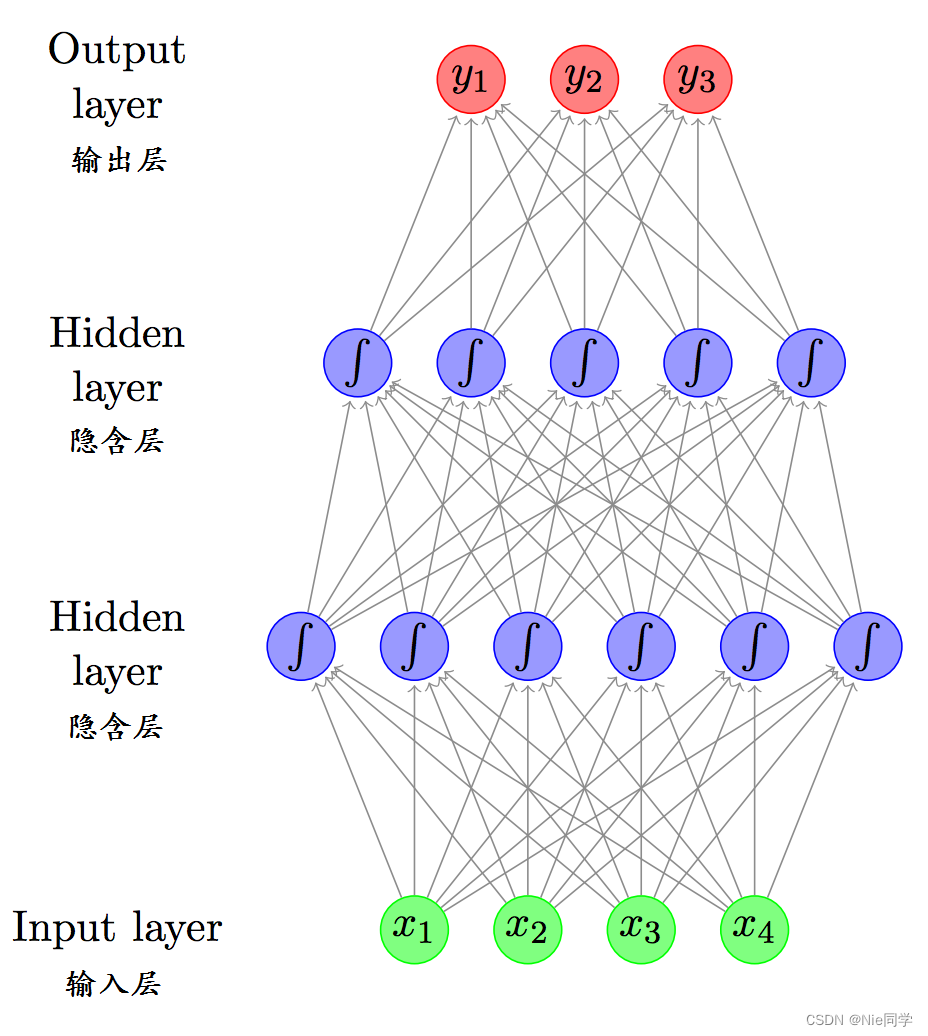
每层神经元与下一层神经元全连接,神经元之间不存在同层连接,也不存在跨层连接。这样的网络称为多层前馈神经网络。
误差逆传播算法
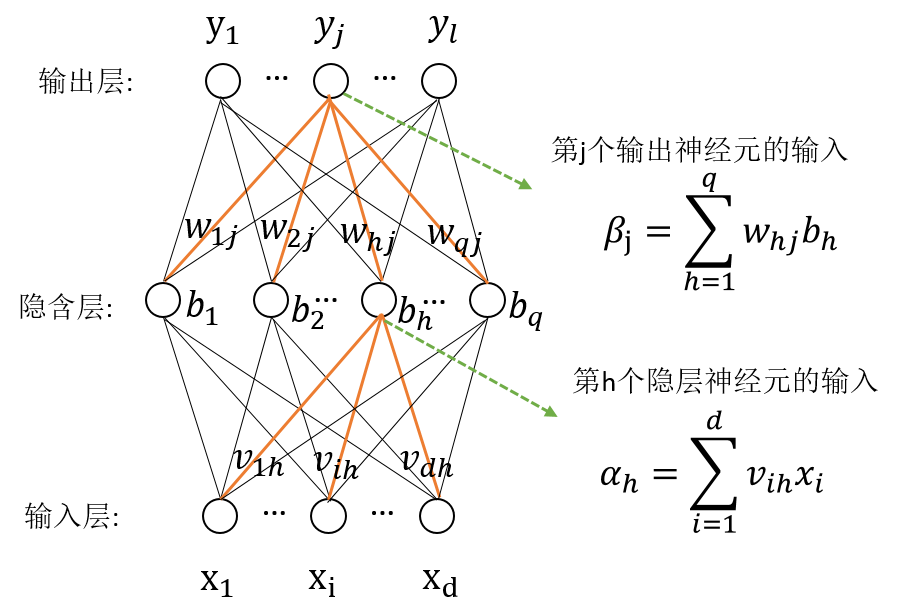
给定数据集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . ( x m , y m ) } D=\{ (x_1,y_1),(x_2,y_2),...(x_m,y_m)\} D={(x1,y1),(x2,y2),...(xm,ym)}, x i ∈ ℜ d , y i ∈ ℜ l x_i\in \Re^d,y_i \in \Re^l xi∈ℜd,yi∈ℜl,即输入样例由 d d d个属性描述,输出样例由 l l l维实值向量。下图给出一个拥有 d d d个输入神经元、 l l l个输出神经元、 q q q个隐层神经元的多层前反馈神经网络。其中输出层第 j j j个神经元的阈值用 θ j \theta_j θj表示,隐层第 h h h个神经元的阈值用 γ h \gamma_h γh表示。输入层第 i i i个神经元与隐层第 h h h个神经元之间的连接权为 v i h v_{ih} vih,隐层第 h h h个神经元与输出层第 j j j个神经元之间的连接权为 w h j w_{hj} whj。记隐层第 h h h个神经元接收到的输入为 α h = ∑ i = 1 d v i h x i \alpha_h=\sum_{i=1}^dv_{ih}x_i αh=∑i=1dvihxi,输出层第 j j j个神经元接收到的输入为 β j = ∑ h = 1 q w h j b h \beta_j=\sum_{h=1}^qw_{hj}b_h βj=∑h=1qwhjbh。其中 b h b_h bh为隐层第 h h h个神经元的输出。
对训练集 ( x k , y k ) (x_k,y_k) (xk,yk),假定神经网络的输出为 y ^ j k = ( y ^ 1 k , y ^ 1 k , . . . , y ^ l k ) \hat y_j^k=(\hat y_1^k,\hat y_1^k,...,\hat y_l^k) y^jk=(y^1k,y^1k,...,y^lk)即
y ^ j k = f ( β j − θ j ) (1) \hat y_j^k=f(\beta_j-\theta_j) \tag{1} y^jk=f(βj−θj)(1)
则网络在 x k , y k x_k,y_k xk,yk上的均方误差为:
E k = 1 2 ∑ j = 1 l ( y ^ j k − y j k ) 2 (2) E_k=\frac{1}{2}\sum_{j=1}^l(\hat y_j^k-y_j^k)^2 \tag{2} Ek=21j=1∑l(y^jk−yjk)2(2)
其中 y ^ j k \hat y_j^k y^jk为神经网络模型输出, y j k y_j^k yjk为训练集实际样例输出。
故在上图网络中共有 ( d + l + 1 ) q + l (d+l+1)q+l (d+l+1)q+l个参数。BP是一个迭代学习算法,在迭代的每一轮中采用广义感知机学习规则对参数进行更新估计,任意参数 v v v的更新估计式为:
v ← v + Δ v (3) v\leftarrow v+\Delta v \tag{3} v←v+Δv(3)
以上图的BP网络中隐层到输出层的连接权 w h j w_{hj} whj为例来进行推导:
BP算法基于梯度下降法,以目标的负梯度方向对参数进行调整,对误差 E k E_k Ek,给定学习率 η \eta η,有:
Δ w h j = − η ∂ E k ∂ w h j (4) \Delta w_{hj}=-\eta \frac{\partial E_k}{\partial w_{hj}} \tag{4} Δwhj=−η∂whj∂Ek(4)
我们注意到 w h j w_{hj} whj先影响到第 j j j个输出层神经元的输入值 β j \beta_j βj,再影响到输出值 y ^ j k \hat y_j^k y^jk,最终影响到 E k E_k Ek,有:
∂ E k ∂ w h j = ∂ E k ∂ y ^ j k ⋅ ∂ y ^ j k ∂ β j ⋅ ∂ β j ∂ w h j (5) \frac{\partial E_k}{\partial w_{hj}}=\frac{\partial E_k}{\partial \hat y_j^k}\cdot \frac{\partial \hat y_j^k}{\partial \beta_j}\cdot \frac{\partial \beta_j}{\partial w_{hj}} \tag{5} ∂whj∂Ek=∂y^jk∂Ek⋅∂βj∂y^jk⋅∂whj∂βj(5)
根据 β j = ∑ h = 1 q w h j h h \beta_j=\sum_{h=1}^qw_{hj}h_h βj=∑h=1qwhjhh的定义,显然有:
∂ β j ∂ w h j = b h (6) \frac{\partial \beta_j}{\partial w_{hj}}=b_h \tag{6} ∂whj∂βj=bh(6)
又因为 s i g m o i d sigmoid sigmoid函数有一个很好的数学性质:
f ′ ( x ) = f ( x ) ( 1 − f ( x ) ) (7) f^\prime(x)=f(x)(1-f(x)) \tag{7} f′(x)=f(x)(1−f(x))(7)
根据式子(1)和(2),有:
g j = − ∂ E k ∂ y ^ j k ⋅ ∂ y ^ j k ∂ β j = − ( y ^ j k − y j k ) f ′ ( β j − θ j ) = y ^ j k ( 1 − y ^ j k ) ( y j k − y ^ j k ) (8) \begin{align*} g_j & = -\frac{\partial E_k}{\partial \hat y_j^k}\cdot \frac{\partial \hat y_j^k}{\partial \beta_j} \\ & = -(\hat y_j^k-y_j^k)f^\prime(\beta_j-\theta_j) \\ & = \hat y_j^k(1-\hat y_j^k)(y_j^k-\hat y_j^k) \end{align*} \tag{8} gj=−∂y^jk∂Ek⋅∂βj∂y^jk=−(y^jk−yjk)f′(βj−θj)=y^jk(1−y^jk)(yjk−y^jk)(8)
其中 E k = 1 2 ∑ j = 1 l ( y ^ j k − y j k ) 2 E_k=\frac{1}{2}\sum_{j=1}^l(\hat y_j^k-y_j^k)^2 Ek=21∑j=1l(y^jk−yjk)2,那么 ∂ E k ∂ y ^ j k = y ^ j k − y j k \frac{\partial E_k}{\partial \hat y_j^k}=\hat y_j^k-y_j^k ∂y^jk∂Ek=y^jk−yjk。 y ^ j k = f ( β j − θ j ) \hat y_j^k=f(\beta_j-\theta_j) y^jk=f(βj−θj),那么 ∂ y ^ j k ∂ β j = f ′ ( β j − θ j ) = f ( β j − θ j ) ⋅ ( 1 − f ( β j − θ j ) ) = y ^ j k ⋅ ( 1 − y ^ j k ) \frac{\partial \hat y_j^k}{\partial \beta_j}=f^\prime(\beta_j-\theta_j)=f(\beta_j-\theta_j)\cdot(1-f(\beta_j-\theta_j))=\hat y_j^k\cdot (1-\hat y_j^k) ∂βj∂y^jk=f′(βj−θj)=f(βj−θj)⋅(1−f(βj−θj))=y^jk⋅(1−y^jk)
将(6)和(8)带入(5)中有:
∂ E k ∂ w h j = g j ⋅ b h (9) \frac{\partial E_k}{\partial w_{hj}}=g_j\cdot b_h \tag{9} ∂whj∂Ek=gj⋅bh(9)
再将(9)带入(4)中,得到BP算法 中关于 w h j w_{hj} whj的更新公式:
Δ w h j = − η g j b h (10) \Delta w_{hj}=-\eta g_jb_h \tag{10} Δwhj=−ηgjbh(10)
同理可得:
Δ θ j = − η g j (11) \Delta\theta_j=-\eta g_j \tag{11} Δθj=−ηgj(11)
Δ v i h = η e h x i (12) \Delta v_{ih}=\eta e_hx_i \tag{12} Δvih=ηehxi(12)
Δ γ h = − η e h (13) \Delta \gamma_h=-\eta e_h \tag{13} Δγh=−ηeh(13)
其中
e h = − ∂ E k ∂ b h ⋅ ∂ b h ∂ α h = − ∑ j = 1 l ∂ E k ∂ β j ⋅ ∂ β j ∂ b h f ′ ( α h − γ h ) = ∑ j = 1 l w h j g j f ′ ( α h − γ h ) = b h ( 1 − b h ) ∑ j = 1 l w h j g j (14) \begin{align*} e_h & = -\frac{\partial E_k}{\partial b_h}\cdot \frac{\partial b_h}{\partial \alpha_h} \\ & = -\sum_{j=1}^l \frac{\partial E_k}{\partial \beta_j}\cdot\frac{\partial \beta_j}{\partial b_h}f^\prime(\alpha_h-\gamma_h) \\ & = \sum_{j=1}^lw_{hj}g_jf^\prime(\alpha_h-\gamma_h) \\ & = b_h(1-b_h)\sum_{j=1}^lw_{hj}g_j \end{align*} \tag{14} eh=−∂bh∂Ek⋅∂αh∂bh=−j=1∑l∂βj∂Ek⋅∂bh∂βjf′(αh−γh)=j=1∑lwhjgjf′(αh−γh)=bh(1−bh)j=1∑lwhjgj(14)
其中 b h b_h bh是隐层神经元的输出 b h = f ( α h − γ h ) b_h=f(\alpha_h-\gamma_h) bh=f(αh−γh), γ h \gamma_h γh是隐层神经元的阈值, α h \alpha_h αh是隐层神经元的输入。
直到所有参数调整至累计误差最小即:
E m i n = 1 m ∑ k = 1 m E k (15) E_{min}=\frac{1}{m}\sum_{k=1}^mE_k \tag{15} Emin=m1k=1∑mEk(15)
缓解过拟合化
由于BP神经网络强大的表示能力,BP神经网络经常遭遇过拟合化,其训练误差持续降低,但测试误差却可能上升。共有两种策略来缓解BP网络的过拟合化。
- 早停:基本思想是在训练过程中监测验证集(一部分未参与训练的数据)上的性能,并在验证集性能达到最优时停止训练,而不是继续训练直到训练误差降为零。
- 正则化:正则化通过修改损失函数,向优化过程中引入额外的惩罚项,从而限制模型的复杂性。这有助于防止神经网络对训练数据过度拟合。在神经网络中,L2(范数) 正则化的损失函数,则误差目标函数为:
E = λ 1 m ∑ k = 1 m E k + ( 1 − λ ) ∑ i w i 2 (16) E=\lambda\frac{1}{m}\sum_{k=1}^mE_k+(1-\lambda)\sum_{i}w_i^2 \tag{16} E=λm1k=1∑mEk+(1−λ)i∑wi2(16)
其中 λ ∈ ( 0 , 1 ) \lambda \in (0,1) λ∈(0,1),用来对经验风险和结构风险进行折中处理。其中经验风险为 1 m ∑ k = 1 m E k \frac{1}{m}\sum_{k=1}^mE_k m1∑k=1mEk,结构风险为 ∑ i w i 2 \sum_{i}w_i^2 ∑iwi2。
结论
在神经网络领域,BP神经网络是一种重要的前馈神经网络,以其在模式学习和逼近函数方面的优越性而备受关注。本文深入探讨了BP神经网络的基本原理和数学模型,通过对其公式的详细推导,为读者提供了清晰的理论基础。
文章首先介绍了M-P神经元模型,将其抽象为神经网络的基本组成单元。激活函数的选择是神经网络设计中关键的一步,文中提到了理想中的激活函数以及实际中常用的 s i g m o i d sigmoid sigmoid函数。
多层前馈神经网络的结构被详细介绍,说明了其层级结构和连接方式。这种结构的神经网络被广泛应用于各个领域,能够处理非线性关系,通过训练调整网络参数,实现对复杂模型的逼近,具有较强的自适应性和泛化能力。
误差逆传播算法是BP神经网络训练的核心,文章通过数学推导详细解释了权重和阈值的更新过程。梯度下降法是其中的关键步骤,通过计算误差对参数的偏导数,实现对参数的调整。
然后,文章提到了BP神经网络容易面临的问题之一,即过拟合。为了缓解过拟合,介绍了两种常用的方法:早停和正则化。早停通过在训练过程中监测验证集性能,及时停止训练,避免过度拟合。正则化通过修改损失函数引入额外的惩罚项,限制模型复杂性,有助于防止神经网络对训练数据过度拟合。
实验分析
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neural_network import MLPRegressor
from sklearn.metrics import mean_squared_error
import matplotlib.pyplot as plt# 读入数据集
data = pd.read_csv('data/predict_room_price.csv')
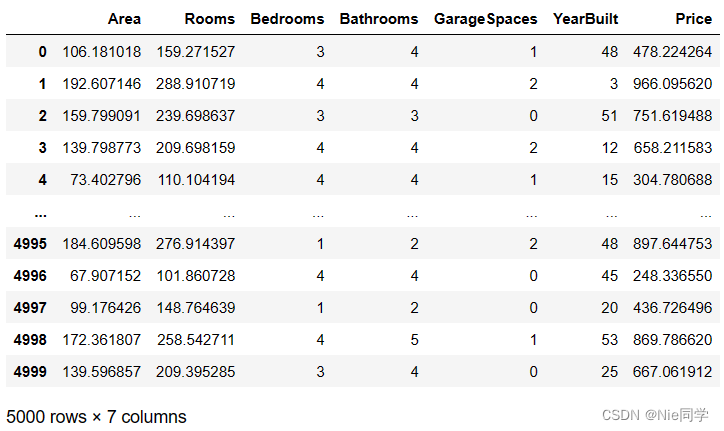
进行数据的预处理
# 特征和标签
X = data.drop('Price', axis=1)
y = data['Price']# 数据标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)# 划分数据集
X_train, X_temp, y_train, y_temp = train_test_split(X_scaled, y, test_size=0.3, random_state=42)
X_valid, X_test, y_valid, y_test = train_test_split(X_temp, y_temp, test_size=0.5, random_state=42)
构建神经网络模型
# 创建BP神经网络模型
model = MLPRegressor(hidden_layer_sizes=(20, 20), max_iter=1000, random_state=42, alpha=0.01, learning_rate='adaptive')
训练、预测并评估模型性能
# 训练模型
model.fit(X_train, y_train)# 在验证集上预测
y_valid_pred = model.predict(X_valid)# 评估模型性能
valid_loss = mean_squared_error(y_valid, y_valid_pred)
print(f'Validation Loss: {valid_loss}')# 在测试集上预测
y_test_pred = model.predict(X_test)# 评估模型性能
test_loss = mean_squared_error(y_test, y_test_pred)
print(f'Test Loss: {test_loss}')# 绘制损失曲线
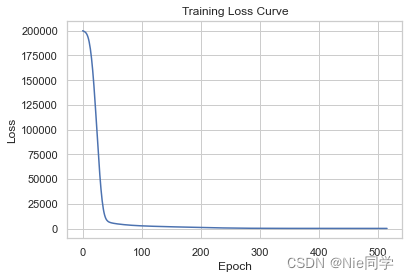
plt.plot(model.loss_curve_)
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('Training Loss Curve')
plt.show()
Validation Loss: 429.78130878683345
Test Loss: 436.7118813730095
residuals = y_test - y_test_pred
plt.scatter(y_test, residuals)
plt.axhline(y=0, color='r', linestyle='--')
plt.xlabel('True Values')
plt.ylabel('Residuals')
plt.title('Residuals Plot on Test Set')
plt.show()
from sklearn.metrics import r2_scorer2_valid = r2_score(y_valid, y_valid_pred)
print(f'R2 Score on Validation Set: {r2_valid}')r2_test = r2_score(y_test, y_test_pred)
print(f'R2 Score on Test Set: {r2_test}')
R2 Score on Validation Set: 0.9939169086519464
R2 Score on Test Set: 0.9934083540996065
由上述评价指标可知:
-
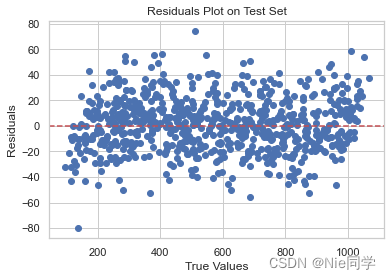
残差图:
- 散点在区间[-80, 80]内,说明模型的预测相对较为准确,大多数样本的预测误差在这个范围内。
- 点集中在[-20, 20]上,表示大部分样本的残差(实际值与预测值之差)都集中在这个范围内,这也表明模型的整体性能较好。
-
Validation Loss 和 Test Loss:非常低的Validation Loss和Test Loss,说明模型在验证集和测试集上都取得了很好的性能。这表明模型对数据的拟合效果很好,预测值与实际值之间的误差很小。
-
R2 Score on Validation Set 和 Test Set:非常接近于1的R2 Score,表明模型对于验证集和测试集的解释方差非常高。R2 Score是一个用于评估模型拟合程度的指标,接近1表示模型能够很好地解释目标变量的变异性。
总体来说,根据残差图、Validation Loss、Test Loss以及R2 Score的结果,模型表现出色,能够很好地拟合数据并具有较高的泛化能力。
相关文章:

BP神经网络(公式推导+举例应用)
文章目录 引言M-P神经元模型激活函数多层前馈神经网络误差逆传播算法缓解过拟合化结论实验分析 引言 人工神经网络(Artificial Neural Networks,ANNs)作为一种模拟生物神经系统的计算模型,在模式识别、数据挖掘、图像处理等领域取…...

Word不同部分(分节)设置页眉和页码的使用指南——附案例操作
Word页眉和页码分节设置的使用指南 目录 Word页眉和页码分节设置的使用指南摘要1. 插入分节符2. 设置不同的页眉3. 设置不同的页码4. 调整页码的起始值5. 删除或更改分节6. 预览和调整 摘要 在撰写word文档时,我们经常需要在不同的部分应用不同的页眉和页码格式。在…...

Ubuntu按转发HDF5
源码编译流程 下载源代码 wget https://hdf-wordpress-1.s3.amazonaws.com/wp-content/uploads/manual/HDF5/HDF5_1_14_3/src/hdf5-1.14.3.zip 解压 unzip hdf5-1.14.3.zip 进入解压后的目录 cd hdf5-1.14.3 编译 依次执行下面的命令 ./configure --prefix/usr/local/hdf5…...
HCIP OSPF实验
任务: 1.使用三种解决ospf不规则区域的方法 2.路由器5、6、7、8、15使用mgre 3.使用各种优化 4.全网可达 5.保证更新安全 6.使用地址为172.16.0.0/16合理划分 7.每个路由器都有环回 拓扑图&IP划分如下: 第一步,配置IP&环回地址…...
Linux上如何一键安装软件?yum源是什么?Linux如何配置yum源?
这几个问题是Linux操作的入门问题,但是确实也会让刚上手Linux小伙伴头疼一阵,故特有此文,希望能对刚入门的小伙伴有一些帮助~ 众所周知 在linux上在线安装软件需要用到yum命令,经常下述命令来安装 yum install [-y] 包名 #-y的…...

Egg框架搭建后台服务【1】
需求 博客系统升级,本来是用 express 写的,最近发现 Egg 不错,正好学习升级一下。边学边写。 Ps:相同的功能,迭代的写法,由浅入深,做个记录。 开发 初始化 安装 node版本需要 >14.20.0…...
)
Unity的Camera类——视觉掌控与深度解析(下)
前言 欢迎阅读本篇博客,这章我们将深入探讨 Unity 游戏引擎中 Camera 类的委托和枚举。摄像机在游戏开发中扮演着关键角色,它不仅定义了玩家视角的窗口,还影响着游戏的视觉表达和整体体验。理解和正确使用 Camera 类的枚举和委托,…...

【模型评估 06】超参数调优
对于很多算法工程师来说,超参数调优是一件非常头疼的事情。除了根据经验设定所谓的“合理值”之外,一般很难找到合理的方法去寻找超参数的最优取值。而与此同时,超参数对于模型效果的影响又至关重要。有没有一些可行的办法去进行超参数的调优…...

Matlab 字符识别OCR实验
Matlab 字符识别实验 图像来源于屏幕截图,要求黑底白字。数据来源是任意二进制文件,内容以16进制打印输出,0-9a-f’字符被16个可打印字符替代,这些替代字符经过挑选,使其相对容易被识别。 第一步进行线分割和字符分割…...

Docker Compose 部署 jenkins
Docker Compose 部署 jenkins jenkins 部署 Docker-Compose 部署 version: 3.1 services:jenkins:image: jenkinsci/blueoceanvolumes:- /data/jenkins/:/var/jenkins_home- /var/run/docker.sock:/var/run/docker.sock- /usr/bin/docker:/usr/bin/docker- /usr/lib/x86_64-…...

QT:使用QStyle实现QMenu的滚动效果
项目中,使用QMenu,多个QAction时 超出页面范围,需要菜单栏可以上下滚动。 实际QMenu是带滚动的,但是要知道怎么使用 还是需要查看QT源码,现在简单记录下我的使用方法。 QT源码中:q->style()->style…...

双指针问题——求只包含两个元素的最长连续子序列(子数组)
一,题目描述 你正在探访一家农场,农场从左到右种植了一排果树。这些树用一个整数数组 fruits 表示,其中 fruits[i] 是第 i 棵树上的水果 种类 。 你想要尽可能多地收集水果。然而,农场的主人设定了一些严格的规矩,你必…...
Unity组件开发--短连接HTTP
1.网络请求管理器 using LitJson; using Cysharp.Threading.Tasks; using System; using System.Collections; using System.Collections.Generic; using UnityEngine; using UnityEngine.Networking; using UnityEngine.Events;using System.Web; using System.Text; using Sy…...

真正的强大,原来是不动声色的
当一个人走过了绝境,他就会发现,真正的强大,原来是不动声色的。 他会停止一切自证,不再解释,话越来越少,眼神越来越坚定。 他不再模棱两可,唯唯诺诺,而是敢于断然拒绝,…...

git 查看tag和创建tag以及上传tag命令
文章目录 git 查看tag和创建tag以及上传tag命令git tagtag操作常用命令 git 查看tag和创建tag以及上传tag命令 git tag 如果你达到一个重要的阶段,并希望永远记住那个特别的提交快照,你可以使用 git tag 给它打上标签。 Git 的 tag 功能是一个非常有用…...
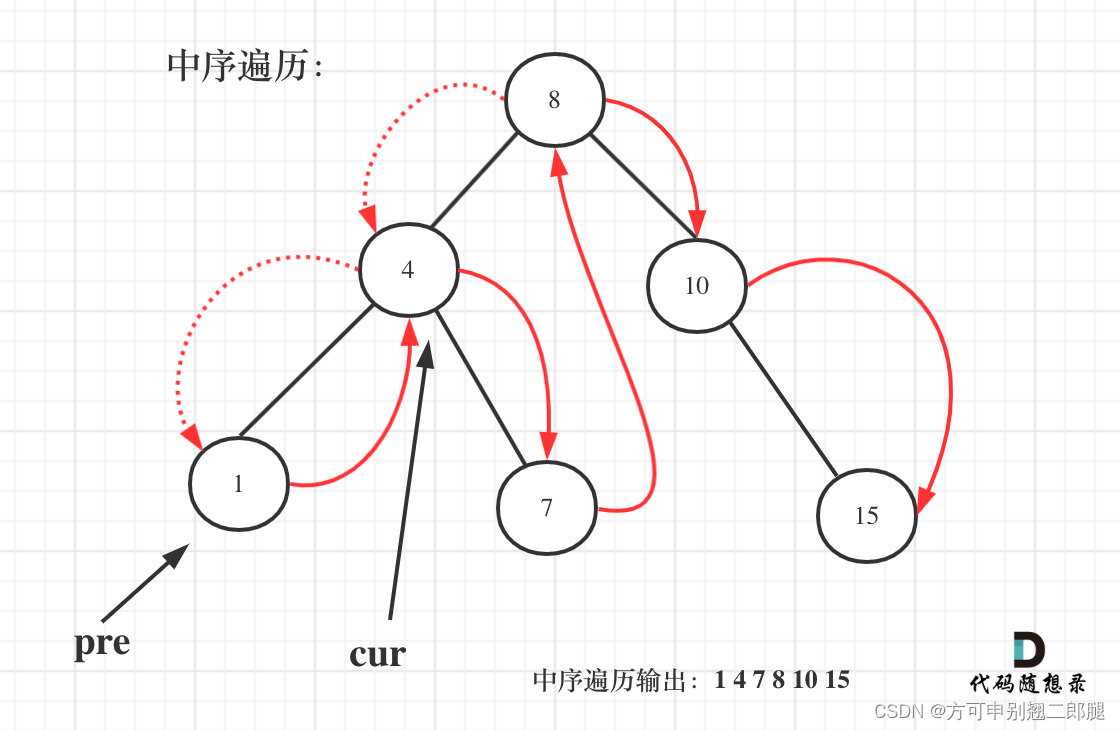
代码随想录二刷 |二叉树 | 二叉搜索树的最小绝对差
代码随想录二刷 |二叉树 | 二叉搜索树的最小绝对差 题目描述解题思路 & 代码实现递归法迭代法 题目描述 530.二叉搜索树的最小绝对差 给你一棵所有节点为非负值的二叉搜索树,请你计算树中任意两节点的差的绝对值的最小值。 示例&#…...

【Linux】Linux 系统编程——tree 命令
文章目录 1. 命令概述2. 命令格式3. 常用选项4. 相关描述4.1 tree 命令安装 5. 参考示例5.1 创建树形目录5.2 使用 tree 命令查看树形目录 1. 命令概述 tree 命令用于在命令行界面以树状图形式显示目录及其子目录的内容。这个命令递归地列出所有子目录,并可选择显示…...

Android简单控件
1.文本显示 设置文本内容的两种方式: 在XML文件中通过属性 android:text 设置文本 <resources><string name"app_name">chapter03</string><string name"hello">你好,世界</string> </resources&…...
【Java 干货教程】Java实现分页的几种方式详解
一、前言 无论是自我学习中,还是在工作中,固然会遇到与前端搭配实现分页的功能,发现有几种方式,特此记录一下。 二、实现方式 2.1、分页功能直接交给前端实现 这种情况也是有的,(根据业务场景且仅仅只能用于数据量…...
关于Python里xlwings库对Excel表格的操作(三十一)
这篇小笔记主要记录如何【如何使用“Chart类”、“Api类"和“Axes函数”设置绘图区外框线型、颜色、粗细及填充颜色】。前面的小笔记已整理成目录,可点链接去目录寻找所需更方便。 【目录部分内容如下】【点击此处可进入目录】 (1)如何安…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...
