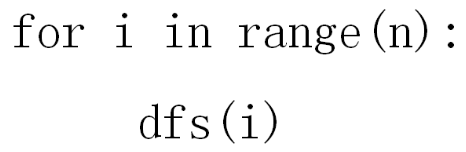图论初入门
目录
一、前言
二、图的概念
三、例题及相关概念
1、全球变暖(2018年省赛,lanqiao0J题号178)
2、欧拉路径
3、小例题
4、例题(洛谷P7771)
一、前言
本文主要讲了树与图的基本概念,图的存储、DFS遍历,欧拉路与欧拉回路以及相关例题。
二、图的概念
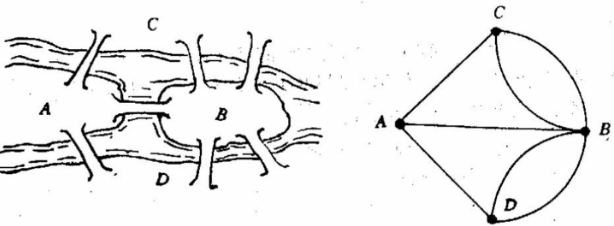
- 图:由点 (node,或者vertex) 和连接点的边 (edge) 组成。
- 图是点和边构成的网。
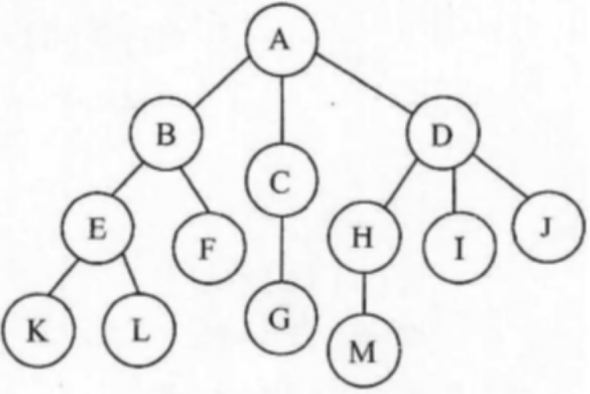
- 树 (是一种特殊的图),即连通无环图
- 树的结点从根开始,层层扩展子树,是一种层次关系,这种层次关系,保证了树上不会出现环路。
- 两点之间的路径:有且仅有一条路径。
【图算法的复杂度】
- 和边的数量E、点的数量V相关。
- O(V+E):几乎是图问题中能达到的最好程度。
- O(VlogE)、O(ElogV):很好的算法。
- O(v^2)、O(E^2)或更高:不算是好的算法。
- 例:最短路径、树的LCA(最近公共祖先)
【图的存储】
能快速访问:图的存储,能让程序很快定位结点 u 和 v 的边 (u,v)。
- 数组存边:简单、空间使用最少;无法快递定位
- 邻接矩阵:简单、空间使用最大;定位最快
- 邻接表:空间很少,定位较快
- 链式前向星:空间更少,定位较快
【数组存边】
优点:简单、最省空间。
缺点:无法定位某条边。
应用:最小生成树的kruskal算法
e=[] for i in range(m):u,v,w=map(int,input().split())e.append((u,v,w))【邻接矩阵】
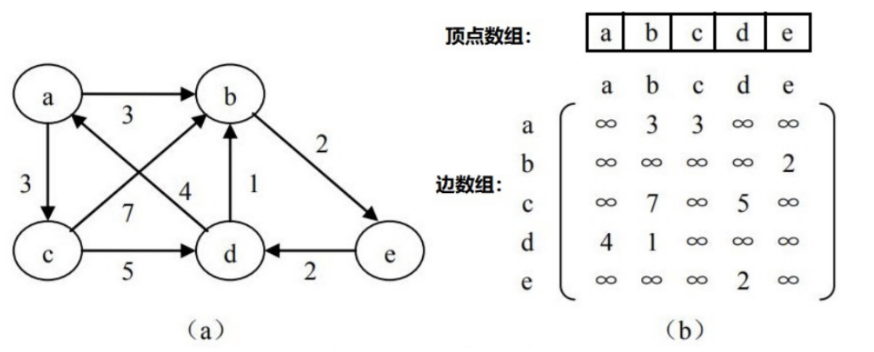
- 二维数组:graph[NUM][NUM]
- 无向图:graph[i][j] = graph[j][i]
- 有向图:graph[i][j] != graph[j][i]
- 权值:graph[i][j] 存结点 i 到 j 的边的权值。例如 graph[1][2]=3,graph[2][1]=5 等等
- 用 graph[i][j]=INF 表示 i,j 之间无边。
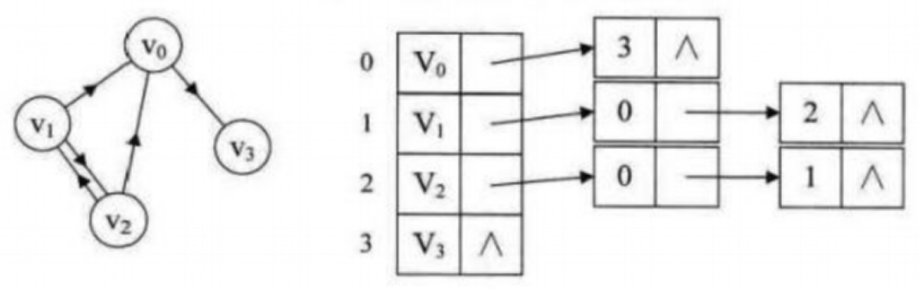
【邻接表】
- 应用场景:大稀疏图
- 优点:
- 存储效率非常高,存储复杂度 O(V+E)
- 能存储重边
edge=[[] for i in range(N+1)] #定义邻接表 for i in range(N):u,v,w=map(int,input().split()) #读入点u,v和边长wedge[u].append((v,w))edge[v].append((u,w)) #无向边 for v,w in edge[u]:【链式前向星】
空间极端紧张,紧凑的存图方法。
相关内容见另一篇博客。
链式前向星_链式前向星 csdn_吕同学的头发不能秃的博客-CSDN博客
【图的遍历和连通性】
- BFS 和 DFS:图论的基本算法。
- 图论算法,或者直按用 BFS 和 DFS 来解决问题,或者用其思想建立新的算法。
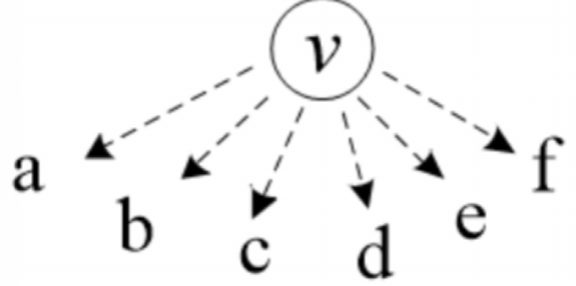
【如何遍历非连通图】
想象有个虛拟结点 v,它连接了所有点
在主程序中对这些点逐一进行 dfs()
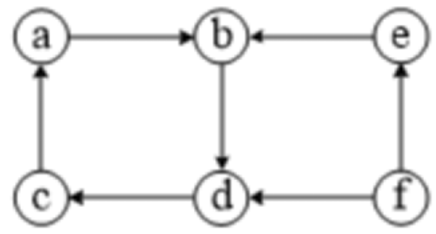
【用DFS判断连通性】
- 对需要的点执行 dfs(),就能找到它连通的点。
- 并查集也能用于检查连通性。
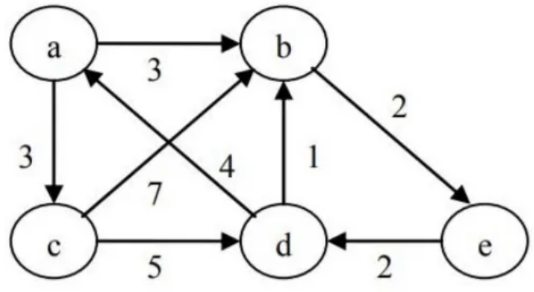
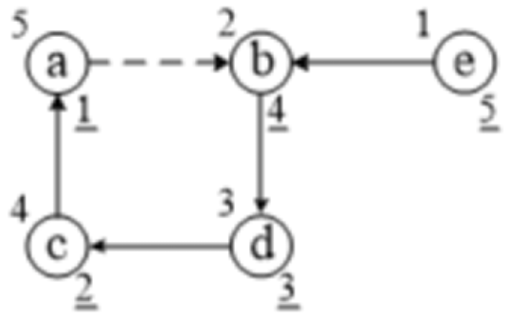
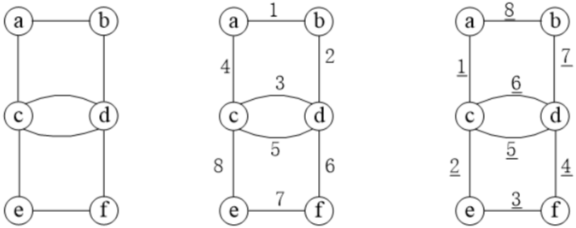
找 e 点的连通性:执行 dfs(e)。
- 访问过程:见结点上面的数字,顺序是:e, b, d, c, a
- 递归返回的结果:见结点下面划线数字,顺序是:a, c, d, b, e
三、例题及相关概念
1、全球变暖(2018年省赛,lanqiao0J题号178)
该题目在我写DFS的笔记时就讲过。
见连接:DFS排列组合与连通性_排列组合dfs_吕同学的头发不能秃的博客-CSDN博客
另外我也独立写了一个题解,后面一对和链接里面的很类似。
import sys
sys.setrecursionlimit(65000)def dfs(x,y):global visglobal mglobal flagglobal Nvis[x][y]=-1d=[(-1,0),(1,0),(0,-1),(0,1)]if m[x-1][y]=='#' and m[x+1][y]=='#' and \m[x][y-1]=='#' and m[x][y+1]=='#':flag=1for i in range(4):dx=x+d[i][0]dy=y+d[i][1]if dx<0 or dx>=N or dy<0 or dy>=N:continueif vis[dx][dy]==0 and m[dx][dy]=='#':dfs(dx,dy)N=int(input())
vis=[[0]*(N+1) for _ in range(N+1)]
m=[]
for _ in range(N):m.append(list(input()))cnt=0
for i in range(1,N-1):for j in range(1,N-1):if vis[i][j]==0 and m[i][j]=='#':flag=0dfs(i,j)if flag==0:cnt+=1
print(cnt)
2、欧拉路径
【欧拉路】
- 欧拉路:从图中某个点出发,遍历整个图,图中每条边通过且只通过一次。
- 欧拉回路:起点和终点相同的欧拉路。
欧拉路问题:
1)是否存在欧拉路
2)打印出欧拉路
通过处理度 (degree):一个点上连接的边的数量,称为这个点的度数。
在无向图中,如果度数是奇数,这个点称为奇点,否则称为偶点。
【欧拉路和欧拉回路是否存在】
1)无向连通图的判断条件如果图中的点全都是偶点,则存在欧拉回路;任意一点都可以作为起点和终点。如果只有 2 个奇点,则存在欧拉路,其中一个奇点是起点,另一个是终点。不可能出现有奇数个奇点的无向图。
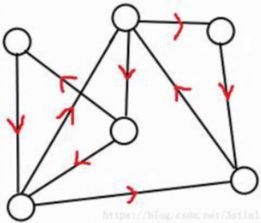
2)有向连通图的判断条件
把一个点上的出度记为 1,入度记为 -1,这个点上所有出度和入度相加,就是它的度数。一个有向图存在欧拉回路,当且仅当该图所有点的度数为零。如果只有一个度数为 1 的点,一个度数为 -1的点,其它所有点的度数为0, 那么存在欧拉路径,其中度数为 1 的是起点,度数为 -1 的是终点。
3、小例题
有 n 个珠子。每个珠子有两种颜色,分布在珠子的两边。一共有 50 种不同的颜色。把这些珠子串起来,要求两个相邻的珠子接触的那部分颜色相同。问是否能连成一个珠串项链?如果能,打印一种连法。
- 答:这一题是典型的无向图求欧拉回路。首先,判断所有的点是否为偶点,如果存在奇点,则没有欧拉回路;其次,判断所给的图是否连通,不连通也不是欧拉回路。
【输出一个欧拉回路】
对一个无向连通图做 DFS,就输出了一个欧拉回路。
【DFS与欧拉回路】
DFS的结果是一个欧拉回路。
4、例题(洛谷P7771)
原题链接:【模板】欧拉路径 - 洛谷
【题目描述】
求有向图字典序最小的欧拉路径
【输入格式】
第一行 2 个整数 n、m,表示有向图的点数和边数。下面 m 行,每行 2 个整数 u、v,表示存在一个有向边边 u->v
【输出格式】
如果不存在欧拉路径,输出一行 No。
否则输出一行 m+1 个数字,表示字典序最小的欧拉路径。
python题解只能过60%
import sys
def dfs(u):i=d[u] #从点u的第一条边i=0开始while i<len(G[u]):d[u]=i+1 #后面继续走u的下一条边dfs(G[u][i]) #继续走这条边的邻居点i=d[u] #第一条边走过了,不再重复走rec.append(u)M=100010
n,m=map(int,input().split())
du=[[0 for _ in range(2)] for _ in range(M)] #记录每个点的入度、出度
G=[[] for _ in range(n+5)] #邻接表存图
d=[0 for _ in range(M)] #d[u]=i;当前走u的第i个边
rec=[] #记录欧拉路for i in range(m):u,v=map(int,input().split())G[u].append(v)du[u][1]+=1 #出度du[v][0]+=1 #入度for i in range(1,n+1):G[i].sort() #对邻居点排序,字典序S=1
cnt=[0,0]
flg=True
for i in range(1,n+1):if du[i][1]!=du[i][0]: #当出度≠入度时,该点就为奇点,此时图存在奇点flg=Falseif du[i][1]-du[i][0]==1:cnt[1]+=1 #cnt[1]用于统计起点数S=iif du[i][0]-du[i][1]==1:cnt[0]+=1
if (not flg) and (not (cnt[0]==cnt[1] and cnt[0]==1)): #存在奇点,且不是只有一个起点和一个终点print("No",end='')sys.exit(0)
dfs(S)
rec=rec[::-1] #反过来,回溯的顺序是欧拉路
#print(''.join(str(i) for i in rec))
print(rec[0],end='')
for i in range(1,len(rec)):print(" %d"%rec[i],end='')
print()
以上,图论初入门
祝好
相关文章:
图论初入门
目录 一、前言 二、图的概念 三、例题及相关概念 1、全球变暖(2018年省赛,lanqiao0J题号178) 2、欧拉路径 3、小例题 4、例题(洛谷P7771) 一、前言 本文主要讲了树与图的基本概念,图的存储、DFS遍历…...

02-Oracle数据库的启动与关闭
本文章主要讲解Oracle数据库的启动与关闭方法,详细讲解启动Oracle的命令,三种启动数据库的方法及区别;关闭数据库的4种方法及他们的区别。 启动和关闭数据库 •数据库没启动前,只有拥有DBA权限或者以sysoper或sysdba身份才能连接到…...

网络营销培训完能达到什么水平?学完能创业吗?
网络营销本身就是一门创业的技术,很多人学习网络营销,往往担心学完以后技术达不到,再工作几年才可以创业,实际这是错误的理解,那么,网络营销培训完能达到什么水平?新手学员参加网络营销培训&…...

大数据技术之——zeppelin数据清洗
一、zeppelin的安装zeppelin解压后进入到conf配置文件界面。修改zeppelin-site.xml[roothadoop02 conf]# cp zeppelin-site.xml.template zeppelin-site.xml[roothadoop02 conf]# vim zeppelin-site.xml将IP地址和端口号设置成自己的修改 zeppelin-env.shexport JAVA HOME/opt/…...
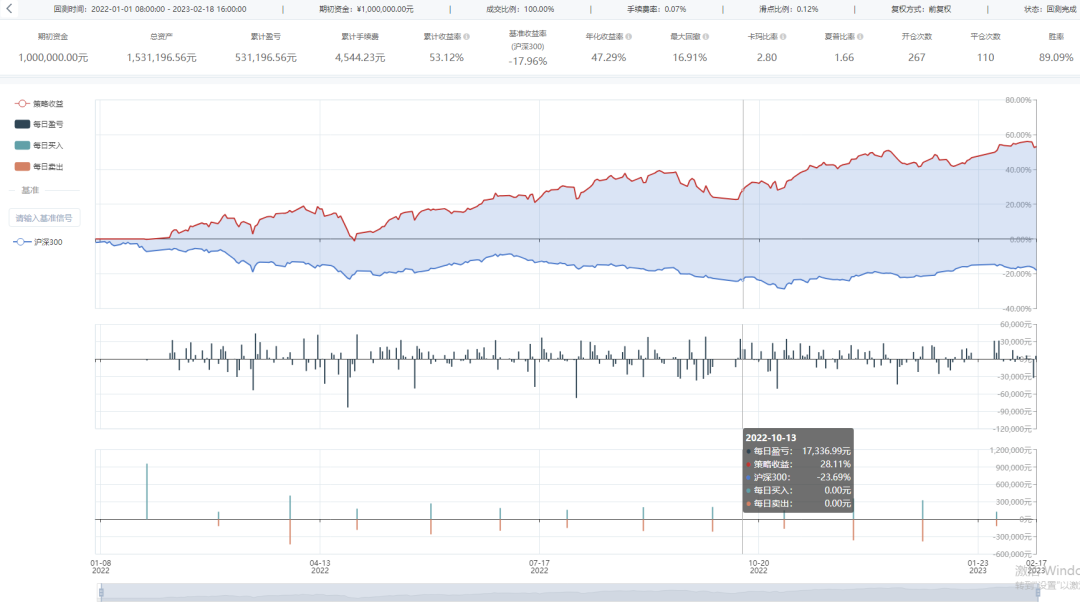
Barra模型因子的构建及应用系列五之NonLinear Size因子
一、摘要 在前期的Barra模型系列文章中,我们构建了Size因子、Beta因子、Momentum因子和Residual Volatility因子,并分别创建了对应的单因子策略,本节文章在该系列下进一步构建NonLinear Size因子。从回测结果看,自2022年以来&…...

C++ 常用命令行开发工具(Linux)
文章目录1、简介2、gcc / g2.1 system(执行shell 命令)2.2 popen(建立管道I/O)2.3 vforkexec(新建子进程)3、clang3.1 下载和安装clang3.2 clang和gcc比较3.2.1 gcc3.2.2 clang3.2.3 LLVM4、make4.1 例子14…...
)
java基础学习 day47(抽象类,抽象方法)
1. 抽象方法 将共性的行为(方法)抽取到父类之后,由于每一个子类执行的内容是不一样的,所以,在父类中不能确定具体的方法体,该方法就可以定义为抽象方法。抽象方法定义格式: public abstract 返…...
)
Java代码弱点与修复之——Open redirect(开放重定向)
弱点描述 Open redirect , 开放重定向,是一种常见的安全漏洞,也被称为“重定向漏洞”。该漏洞通常出现在 Web 应用程序中,攻击者可以利用它将用户重定向到恶意站点,从而进行钓鱼攻击、恶意软件传播、诱骗等活动。 在 Java 中,通过重定向 HTTP 请求来实现应用程序中的跳转…...

Go 指针
指针在编程中,一个内存地址用来定位一段内存。通常地,一个内存地址用一个操作系统原生字(native word)来存储。 一个原生字在32位操作系统上占4个字节,在64位操作系统上占8个字节。 所以,32位操作系统上的理…...
shardingsphere5.1.1分表分库yaml配置 自定义策略
前言通过阅读官方稳定给出示例 https://shardingsphere.apache.org/document一、基本配置示例spring:sharding:datasource:names: ds0, ds1ds0:driver-class-name: com.mysql.jdbc.Driverurl: jdbc:mysql://localhost:3306/db0username: rootpassword: rootds1:driver-class-na…...

“探索未来:VR全景直播技术引领新媒体时代”
随着虚拟现实技术的不断发展,VR全景直播已经成为了越来越受欢迎的直播形式。VR全景直播可以让观众通过虚拟现实设备亲临直播现场,享受身临其境的观看体验。VR全景直播是什么? VR全景直播是虚拟现实技术和直播的结合。相对于传统直播ÿ…...

Spring Cloud(微服务)学习篇(六)
Spring Cloud(微服务)学习篇(六) 2 Sentinel实现流量规则(控制台版) 2.1 变更pom.xml(shop-user-server项目)代码 2.1.1 加入如下依赖 <!--熔断限流--> <dependency><groupId>com.alibaba.cloud</groupId><artifactId>spring-cloud-starter-…...
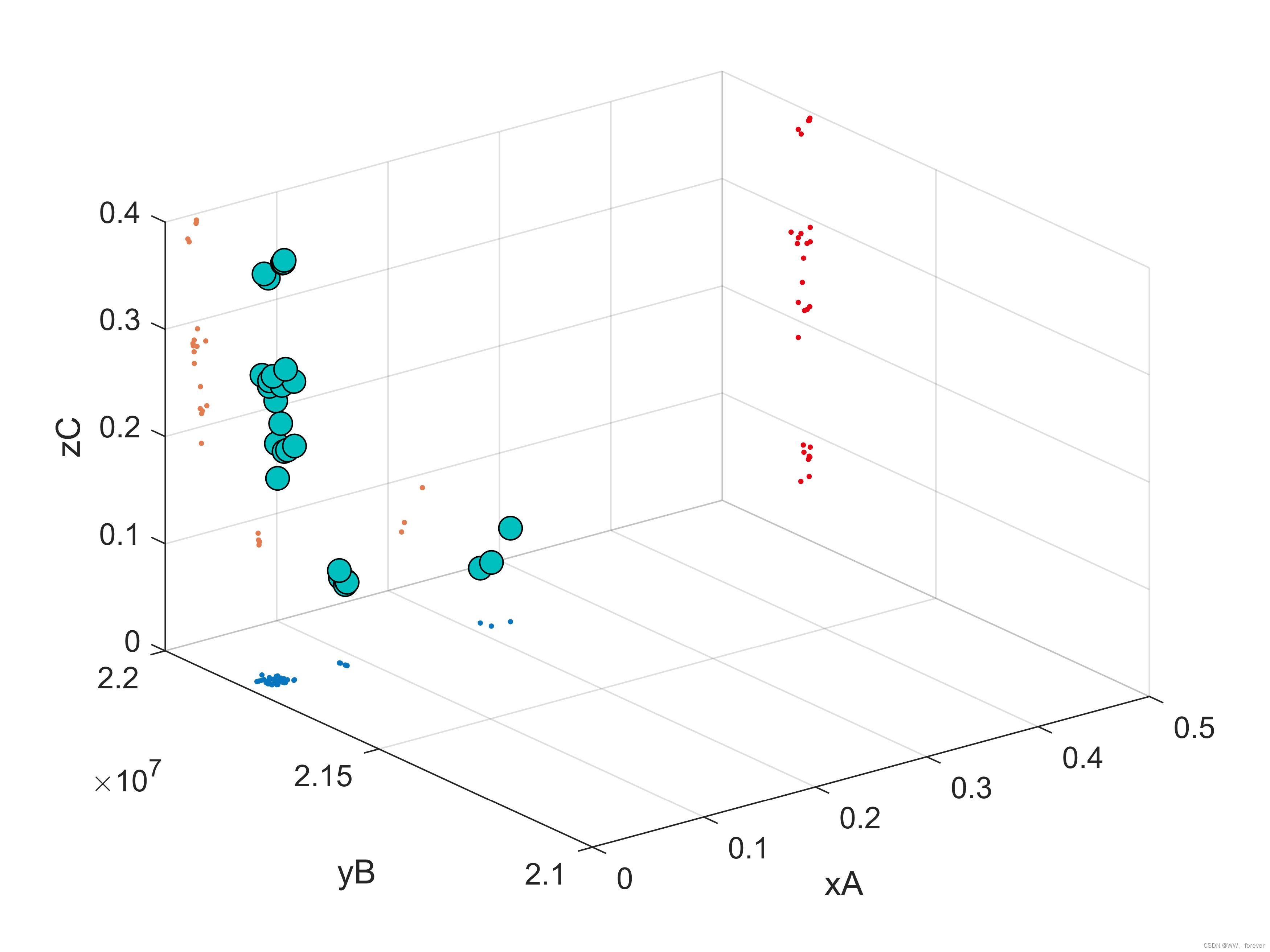
MATLAB-Scatter3-三维散点图投影至XYZ三个平面
MATLAB-Scatter3函数可以绘制立体的三维散点图,但有时候需要在该立体图中分析X-Y-Z三者的关系,即1副图呈现出4个信息,XYZ综合信息、XY信息、XZ信息、YZ信息。现有的Scatter3无法实现该功能,本文可实现Scatter3三维立体散点图在三个…...
Unity/C#------委托与事件(一篇文章彻底搞懂...)
一:委托 所有的代码语言创造者母语都是英语,我们从英语翻译到中文的过程中难免会存在一些不太能还原本意的词,比如我之前一直不理解构造函数和析构函数,只知道这俩货作用相反,直到我看到了它的英文意思,Con…...
别再为 Jenkins 安装烦恼,Docker 帮你轻松解决
前言 大家好,又见面了,我是沐风晓月,本文收录与云原生相关的专栏,以下是我的简介: 🏠个人主页:我是沐风晓月 🧑个人简介:大家好,我是沐风晓月,双…...

汇编语言程序设计(一)
前言 在学习汇编语言之前,我们应该要知道汇编语言他是一门怎么样的语言。汇编语言是直接工作在硬件上的一门编程语言,学习汇编语言之前最好先了解一下计算机硬件系统的结构和工作原理。学习汇编语言的重点是学习如何利用硬件系统的编程结构和指令集进而…...

【uni-app教程】四、UniAPP 路由配置及页面跳转
四、UniAPP 路由配置及页面跳转 (1) 路由配置 uni-app页面路由为框架统一管理,开发者需要在pages.json里配置每个路由页面的路径及页面样式。类似小程序在 app.json 中配置页面路由一样。所以 uni-app 的路由用法与 Vue Router 不同,如仍希望采用 Vue …...
-- ROS控制器图形化界面开发)
ROS从入门到精通系列(二十八)-- ROS控制器图形化界面开发
ROS (Robot Operating System, 机器人操作系统) 作为机器人软件中的通信及控制中间件,提供一系列程序库和工具以帮助软件开发者创建机器人应用软件。它提供了硬件抽象、设备驱动、函数库、可视化工具、消息传递和软件包管理等诸多功能。ROS遵循BSD开源许可协议。 随着机器人智…...
Submodule命令:android如何将自己项目中的某个Module作为gitlab中第三方公共库
一、创建远程公共库 1、Android Studio创建本地仓库 创建一个新的module 在新建module中添加代码(此处示例代码) 右击新建的module,打开新建module的命令行界面, 因为我们只上传这个module的代码,而不是整个项目的代码 命令行中输入以下命令…...

MySQL索引事务
1.索引1.1概念索引是一种特殊的文件,包含着对数据表里所有记录的引用指针。可以对表中的一列或多列创建索引,并指定索引的类型,各类索引有各自的数据结果实现。(这里只用通俗的语言和图片进行介绍)1.2作用数据库中的表…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...